Đề kiểm tra cuối học kỳ 1 Toán 11 năm 2023 – 2024 sở GD&ĐT Bắc Ninh
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra cuối học kỳ 1 môn Toán 11 năm học 2023 – 2024 sở Giáo dục và Đào tạo tỉnh Bắc Ninh
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KỲ 1 BẮC NINH NĂM HỌC 2023 – 2024 Môn: TOÁN – Lớp 11 (Đề có 02 trang)
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
I. PHẦN TRẮC NGHIỆM (3,0 điểm)
Câu 1. Nếu cấp số cộng u có u 4 , u 12 thì công sai của cấp số cộng đó bằng n 1 2 1 A. 8 . B. 3 . C. 8 . D. . 3
Câu 2. Nếu cấp số nhân u có số hạng đầu u 2 và công bội q 3 thì giá trị của u bằng n 1 2 2 A. 5 . B. . C. 6 . D. 1. 3
Câu 3. Cho cấp số cộng u có số hạng đầu là u và công sai d . Với mọi số nguyên dương n 2, n 1
khẳng định nào sau đây đúng? A. u u nd .
B. u u n 1 d . C. u u n 1 d . D. n 1 u u d . n 1 n 1 n 1 n 1
Câu 4. Có bao nhiêu số thực x để ba số 2x 1; x ; 2x 1 theo thứ tự đó lập thành cấp số nhân? A. 1 . B. 2 . C. 3 . D. 4 . 3n 1 Câu 5. lim bằng n n 2 1 A. . B. . C. 3 . D. 0 . 2 1 1 1 Câu 6. Tổng S 1 bằng 2 2 2 2n 5 A. . B. . C. 3 . D. 2 . 3 1x Câu 7. lim bằng x 2 x 2 A. . B. . C. 1. D. 1 .
Câu 8. Khẳng định nào sau đây sai?
A. Nếu k là số nguyên dương lẻ thì lim k x . x
B. Nếu k là số nguyên dương lẻ thì lim k x . x
C. Nếu k là số nguyên dương chẵn thì lim k x . x
D. Nếu k là số nguyên dương thì lim k x . x
Câu 9. Cho hàm số y f x xác định trên khoảng a;b và x a;b . Điều kiện cần và đủ để hàm 0
số y f x liên tục tại điểm x là 0
A. lim f x f x . B. lim f x f x . 0 0 x x 0 x x 0
C. lim f x lim f x .
D. lim f x lim f x f x . 0 x x 0 x x 0 x x 0 x x 0 Trang 1/2
Câu 10. Điều kiện cần và đủ để hai mặt phẳng song song với nhau là
A. Hai mặt phẳng đó cùng song song với một mặt phẳng thứ ba.
B. Hai mặt phẳng đó cùng song song với một đường thẳng.
C. Hai mặt phẳng đó không có điểm chung.
D. Có một mặt phẳng chứa hai đường thẳng phân biệt cùng song song với mặt phẳng còn lại.
Câu 11. Trong một hình lăng trụ tam giác, khẳng định nào dưới đây sai?
A. Các mặt bên là các hình bình hành.
B. Các cạnh bên đôi một song song với nhau.
C. Hai mặt đáy song song với nhau.
D. Các cạnh đáy đôi một song song với nhau.
Câu 12. Cho hình chóp S.ABC . Gọi M,N,P,Q lần lượt là trung điểm của các cạnh SB , SC , AC
và AB . Hình chiếu của tam giác AMN qua phép chiếu song song trên mặt phẳng ABC theo phương chiếu SA là A. A QP . B. A BC . C. SMN . D. S BC .
II. PHẦN TỰ LUẬN (7,0 điểm)
Câu 13. (1,5 điểm) Tính các giới hạn sau: x 1 2 n 1 a) lim 2x 3 ; b) lim ; c) lim . x 2 x 1 x 1 n 2n 3 2 x 5x 6 khi x 3
Câu 14. (1,0 điểm) Xét tính liên tục của hàm số f x x 3 tại điểm x 3 . 1 khi x 3 0
Câu 15. (1,0 điểm) Cho cấp số cộng u có u 3 và công sai q 2 . n 1 a) Tính u . 5
b) Tính tổng 10 số hạng đầu tiên của dãy số trên.
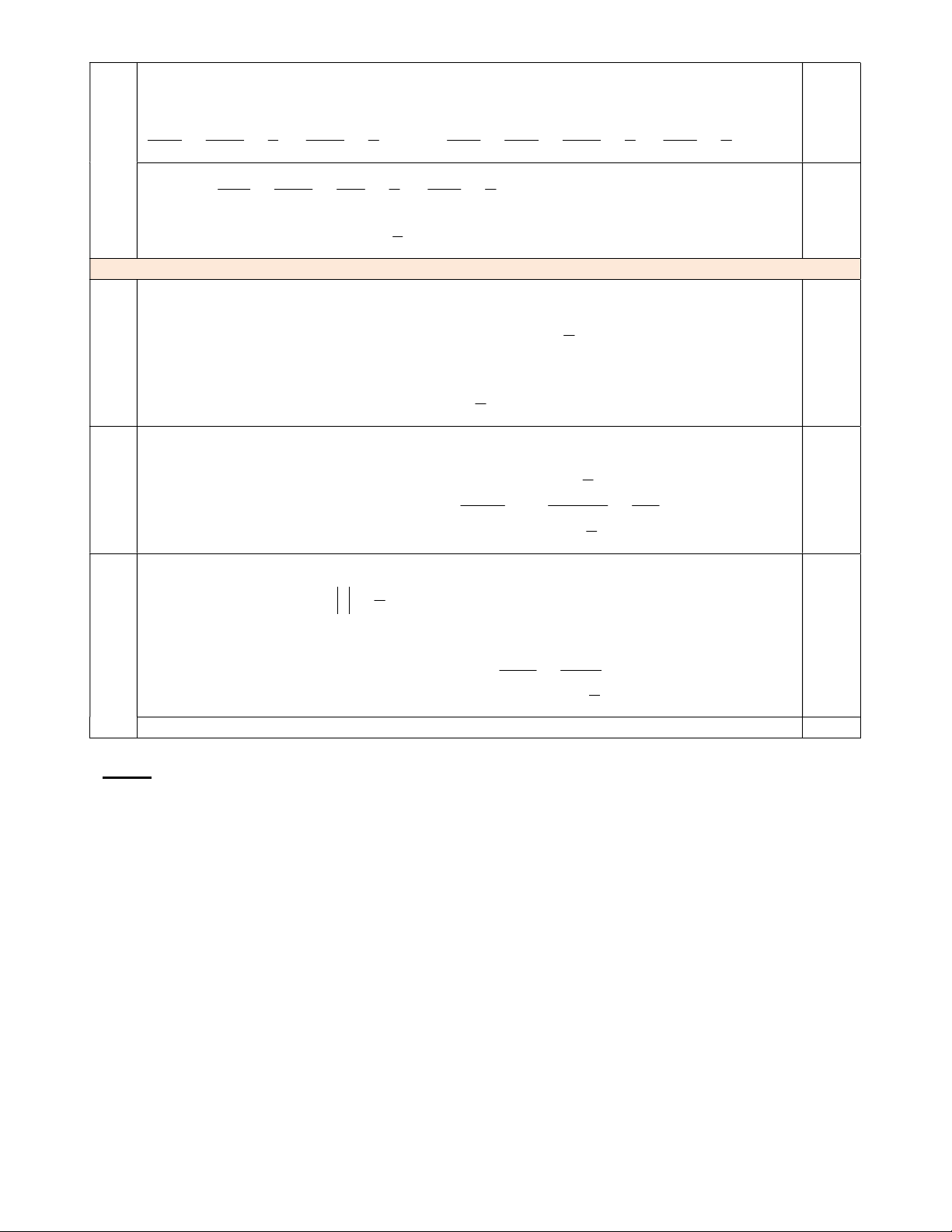
Câu 16. (2,5 điểm) Cho hình hộp ABCD.AB C D
. Gọi M,N lần lượt là trung điểm của AB và C D .
a) Chứng minh AB song song với mặt phẳng CDD C .
b) Chứng minh ADN song song với mặt phẳng B C M .
c) Gọi E,F lần lượt là giao điểm của D B
với các mặt phẳng ADN và B CM. 1 Chứng minh D E BF EF . 2
Câu 17. (1,0 điểm) Người ta thả một viên bi lăn trong một khe thẳng trên một mặt phẳng. Viên bi lăn 3
chậm dần. Giây đầu tiên nó lăn được 2 mét. Mỗi giây sau đó, nó lăn được một đoạn bằng đoạn 4
đường đi được trong giây liền trước đó.
a) Tính quãng đường viên bi lăn được trong 5 giây đầu tiên (làm tròn đến hàng phần chục theo đơn vị mét).
b) Viên bi có thể cách xa vị trí ban đầu 9 mét hay không? -------- Hết -------- Trang 2/2
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM BẮC NINH
KIỂM TRA CUỐI HỌC KỲ 1 NĂM HỌC 2023 – 2024 ¯¯¯¯¯¯¯¯¯¯ Môn: Toán – Lớp 11
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
I. PHẦN TRẮC NGHIỆM (3,0 điểm): Mỗi câu trả lời đúng 0,25 điểm. Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án A C C B C D B B D C D A
II. PHẦN TỰ LUẬN (7,0 điểm) Câu Lời giải sơ lược Điểm 13. (1,5 điểm) a)
lim 2x 3 2 2 3 1 . 0,5 x 2 x 1 x x 1 1 x 1 1 1 b) lim lim lim lim . 0,5 x 1 x 1 x 1
x x x 1 x x x 1 x 2 1 1 1 1 1 1 2 1 2 n 1 n 1 0 1 c) lim lim . 0,5 n 2n 3 n 3 2 0 2 2 n 14. (1,0 điểm) 2 x 5x 6 x 2 x 3 Ta có lim f x lim lim lim x 2 1. 0,5 x3 x3 x3 x3 x 3 x 3
Lại có f 3 1, suy ra lim f x f 3 . x3 0,5
Vậy hàm số f x liên tục tại điểm x 3. 0 15. (1,0 điểm) a)
Ta có u 3 4 2 5 . 5 0,5
Tổng 10 số hạng đầu tiên của dãy là b) 10 S 2 3 9 2 60 0,5 10 2 . 16. (2,5 điểm) Do ABC . D AB C D là hình hộp nên AB C D
là hình bình hành. Suy ra AB C D . Mặt khác C D CDD C a) 1,0 và AB CDD C nên AB CDD C .
Dễ thấy tứ giác ADCB là hình bình hành nên AD B C
. Suy ra AD B CM. 0,5
b) Tứ giác ANCM là hình bình hành nên AN CM AN B C M . 0,5
Hơn nữa AD AN A nên ADN B C M .
Gọi I BD CM , I B D
AN . Suy ra E DI D B , F IB D B . c)
Áp dụng định lí Thales ta có 0,25 D I D N 1 D I 1 D E D I D I 1 D E 1 I B AB 2 D B . Suy ra 3 EB DB D B 3 D B . (1) 4 BF BI BI 1 BF 1 Tương tự FD B D BD 3 BD . (2) 4 0,25 1 Từ (1) và (2) suy ra D E BF EF . 2 17. (1,0 điểm)
Giây thứ nhất, viên bi lăn được quãng đường là u 2 (m). 1 3
Vì mỗi giây sau đó, viên bi di chuyển được một đoạn bằng đoạn đường đi được trong a) 4 0,25
giây liền trước đó nên quãng đường di chuyển của viên bi ở mỗi giây lập thành một cấp số 3
nhân với số hạng đầu u 2 và công bội q . 1 4
Suy ra quãng đường viên bi lăn được trong 5 giây đầu tiên là 5 3 1 5 1q 4 781 0,25
S u u u u u u 2 6,1(m). 5 1 2 3 4 5 1 1q 3 128 1 4
Giả sử quá trình di chuyển của viên bi là vô hạn . 3
Do u là cấp số nhân có q 1 nên u là cấp số nhân lùi vô hạn. n n 4
Vì vậy quãng đường tối đa mà viên bi di chuyển được là 0,25 b) u1 2
S u u u 8 (m). 1 2 n 1q 3 1 4
Vậy viên bi không thể cách vị trí ban đầu 9 (m). 0,25
Lưu ý: Các cách giải khác đáp án, nếu đúng vẫn cho điểm theo các bước tương ứng.
Document Outline
- Toan_11_KTCK1_23_24_De_e0f10
- Toan_11_KTCK1_23_24_DA_3a60f