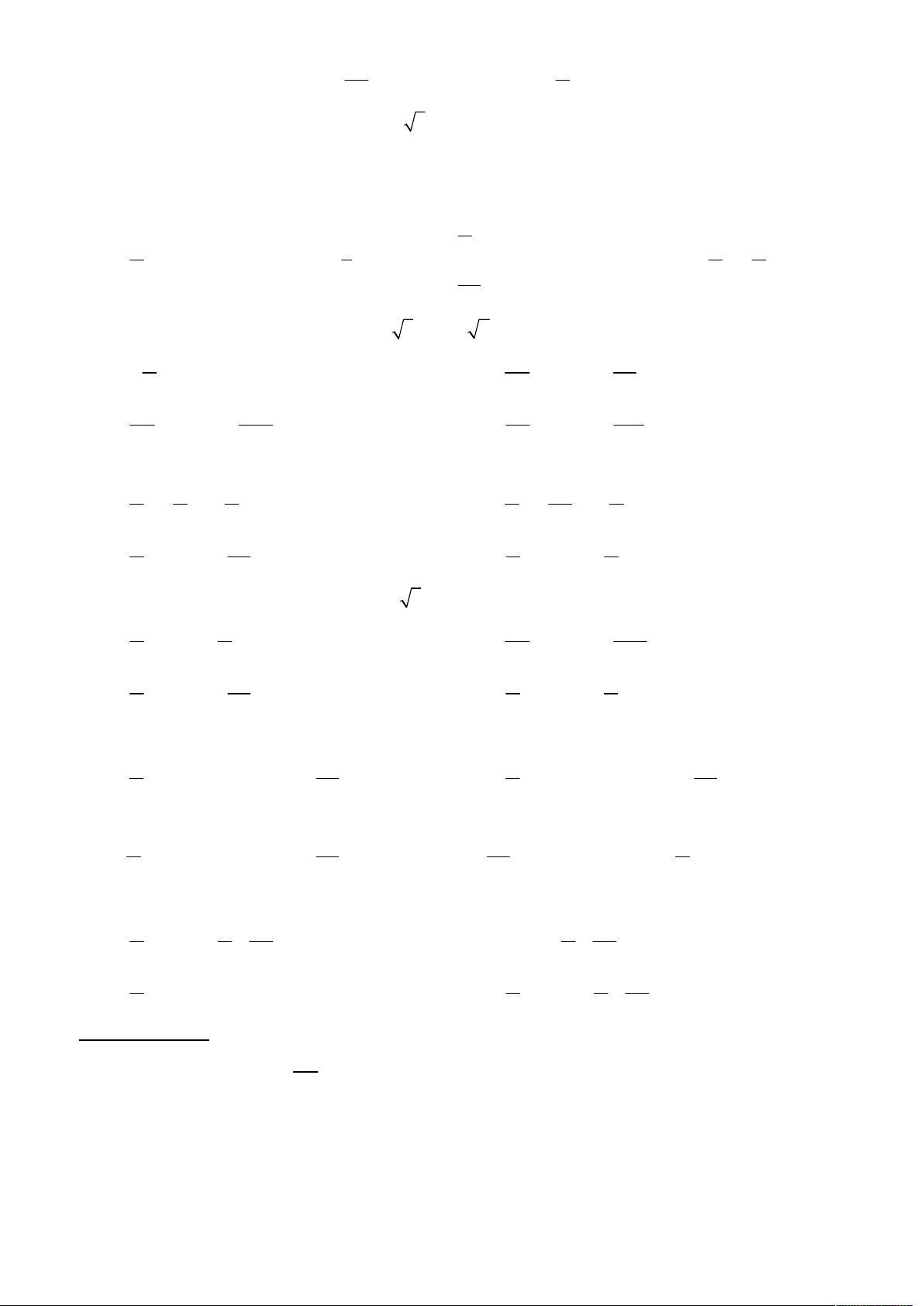




Preview text:
TRƯỜNG THPT NGỌC HỒI
ĐỀ KIỂM TRA ĐẠI SỐ VÀ GIẢI TÍCH 11 – Thời gian 45 phút
Họ và tên học sinh: Lớp: Điểm: MÃ ĐỀ 132
I) TRẮC NGHIỆM (5 ĐIỂM)
Học sinh ghi 1 đáp án lựa chọn vào ô tương ứng trong bảng sau: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Câu 1: Tập giá trị của hàm số y 3 s inx là A. B. C. 2; 2 D. 2; 4
Câu 2: Cho hàm số f (x) sin 3x và 2
g(x) cot x , chọn mệnh đề đúng
A. f(x) là hàm số lẻ, g(x) là hàm lẻ.
B. f(x) là hàm số lẻ, g(x) là hàm chẵn.
C. f(x) là hàm số chẵn, g(x) là hàm lẻ.
D. f(x) là hàm số chẵn, g(x) là hàm chẵn.
Câu 3: Tìm nghiệm dương nhỏ nhất của phương trình: 2
(2 cos x sinx)(1+sinx) = cos x 5 3 A. x B. x C. x D. x 6 3 3 2
Câu 4: Cho phương trình 4sin5x.sinx – 2cos4x - 3 = 0. Tìm số điểm biểu diễn nghiệm của phương trình lên đường tròn lượng giác A. 3 B. 6 C. 12 D. 20
Câu 5: Phương trình nào sau đây vô nghiệm A. 3 s inx osx = - c 2 B. 4s inx 3 o
c sx = -5 C. s inx o c s2018 D. 3 s in2x os2x = - c 3
Câu 6: Tìm tất cả nghiệm phương trình 2 s in x 3 s inx osx = 1 c A. x k ; x
k , k B. x
k 2 ; x
k 2 , k 2 6 2 6 5 5 C. x
k 2 ; x
k 2 , k D. x
k 2 ; x
k 2 , k 6 6 6 6
Câu 7: Tìm tất cả nghiệm phương trình 2 2 2
s in x sin 3x - 2cos 2x = 0 k k A. x k ; x , k
B. x k ; x , k 2 8 2 8 4 k C. x
k , k D. x k ; x , k 2 2 8 4
Câu 8: Tìm tập xác định D của hàm số y cosx
A. D= B. D \ k 2 , k
C. D \ k ,k D. D = \k ,k 2
Câu 9: Trong các hàm số sau đây, hàm số nào là hàm số chẵn
A. y tan2x cot x B. 2 y o
c s x s inx 2 C. y s inx+1 D. y s inx.cos2x
Câu 10: Hàm số y = sin2x đồng biến trên khoảng nào trong các khoảng sau 3 3 A. 0; B. ; C. ; 2 D. ; 4 2 2 2
Câu 11: Tìm số nghiệm của phương trình 2cos x 1 0
với 0 x 2 3 A. 0 B. 2 C. 1 D. 3
Câu 12: Tìm tất cả các giá trị của x để hàm số y = tanx -1 có nghĩa A. x
B. x k 2 , k C. x
k , k D. x
k , k 2 4 1 os c x
Câu 13: Tìm tập xác định D của hàm số y sinx.cosx k
A. D \ {k , k }
B. D \{k 2 , k }
C. D \{- k , k } D. D \{ , k } 2 2
Câu 14: Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y s inx cosx+1 .Tính P = M-m A. P 2 2 B. P 2 C. P 2 D. P=4
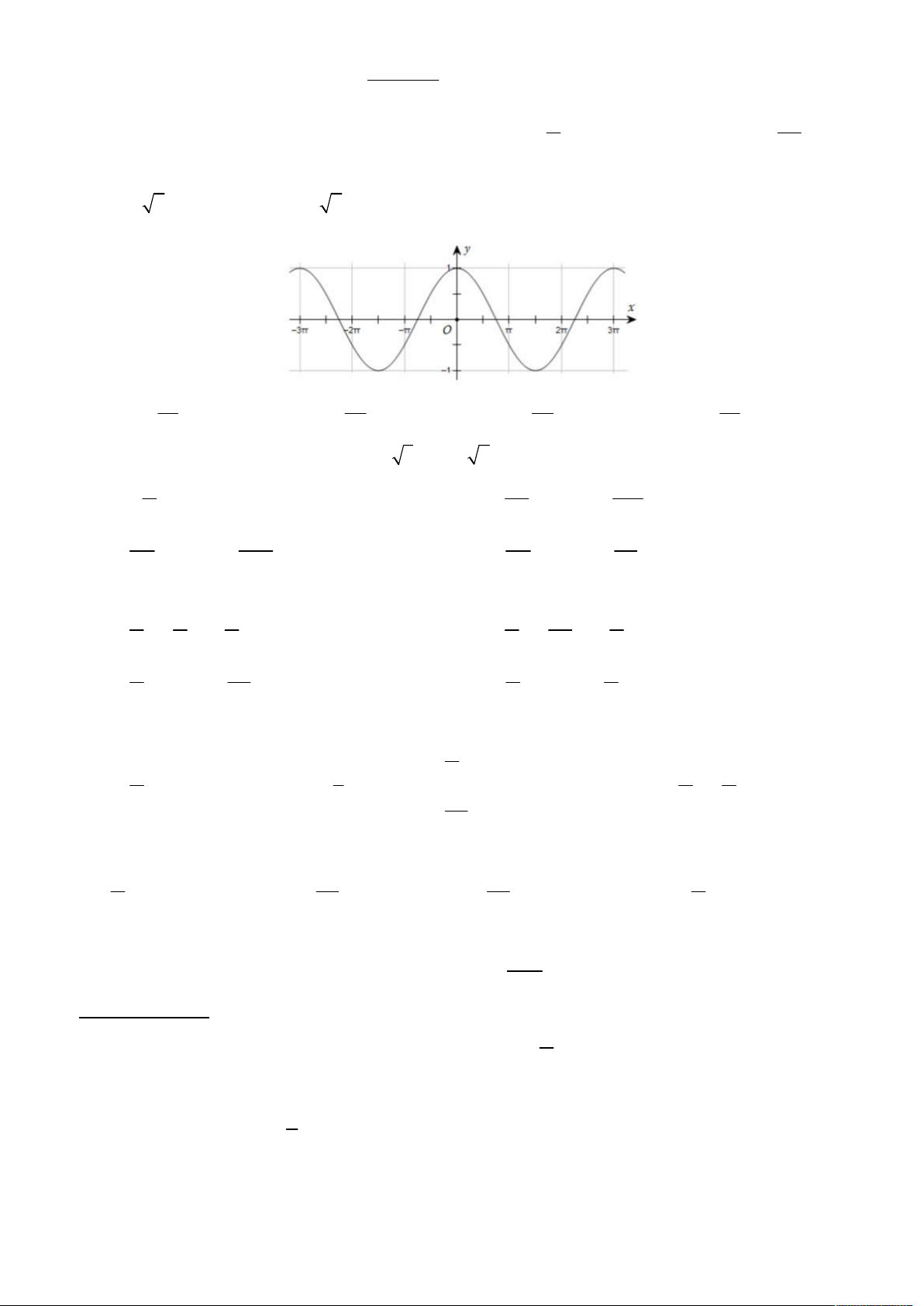
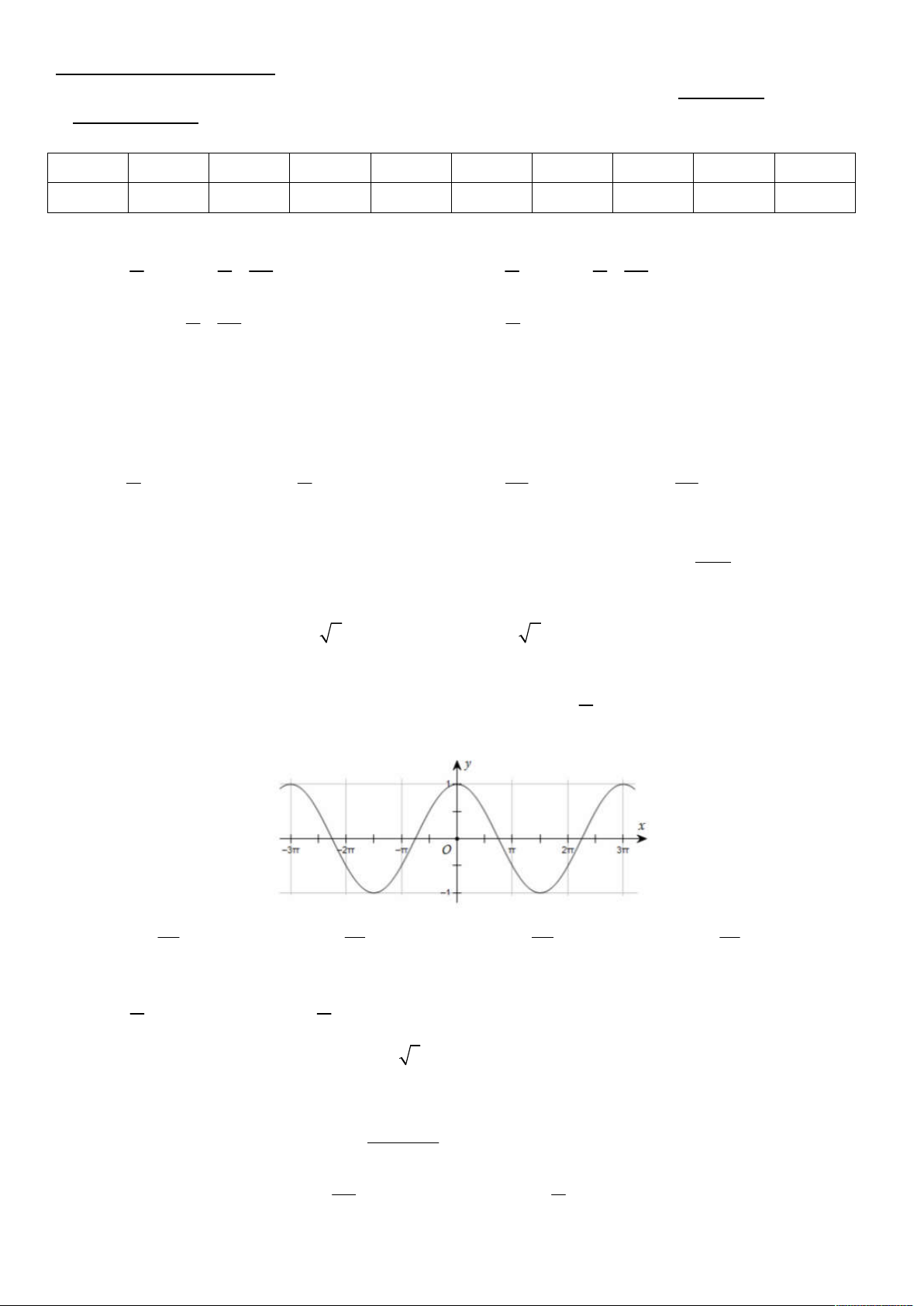
Câu 15: Đường cong trong hình là đồ thị của hàm số nào 3x 2x 2x 3x A. y os c B. y os c C. y sin D. y sin 2 3 3 2
Câu 16: Tìm tất cả nghiệm phương trình s inx 3 osx c = 2 7 13 A. x
k , k B. x
k 2 ; x
k 2 , k 3 12 12 7 5 C. x
k 2 ; x
k 2 , k D. x
k 2 ; x
k 2 , k 12 12 12 12
Câu 17: Tìm tất cả các nghiệm của phương trình sin 2x o c sx 2 A. x k ; x
k , k B. x k ; x
k 2 , k 6 2 2 6 3 2 5 C. x
k 2 ; x
k 2 , k D. x
k 2 ; x
k , k 6 6 6 2
Câu 18: Tìm tất cả các nghiệm của phương trình 2sinx -1 = 0 x k 2 1 6 A. x
k , k B. s inx C. (k ) D. x k , k 6 3 5 6 2 x k 2 6
Câu 19: Hàm số y = sinx và y = cosx cùng đồng biến trên khoảng nào sau đây 3 3 A. ; B. ; C. ; 2 D. 0; 2 2 2 2
Câu 20: Đồ thị của hàm số nào sau đây nhận gốc tọa độ O làm tâm đối xứng s inx A. y . x sinx B. y cosx C. y D. y . x cosx x
II) PHẦN TỰ LUẬN (5 ĐIỂM)
Bài 1 (2 điểm): Tìm nghiệm x (
;5 ) của phương trình: tan(x ) 1 0 4
Bài 2 (3 điểm): Cho phương trình: 2
3sin 2x 4m sin 2x 4 0 (*) 1
a) Giải phương trình (*) với m 4
b) Tìm m để phương trình (*) có nghiệm.
---------------------------------------------------------- HẾT ----------
TRƯỜNG THPT NGỌC HỒI ĐỀ KIỂM TRA ĐẠI SỐ VÀ GIẢI TÍCH 11 – Thời gian 45 phút
Họ và tên học sinh: Lớp: Điểm: MÃ ĐỀ 209
I) TRẮC NGHIỆM (5 ĐIỂM)
Học sinh ghi 1 đáp án lựa chọn vào ô tương ứng trong bảng sau: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Câu 1: Phương trình nào sau đây vô nghiệm A. 3 s inx osx = - c 2 B. s inx o
c s2018 C. 4s inx 3 o c sx = -5 D. 3 s in2x os2x = - c 3
Câu 2: Trong các hàm số sau đây, hàm số nào là hàm số chẵn
A. y s inx.cos2x B. 2 y o
c s x s inx 2 C. y s inx+1
D. y tan2x cot x
Câu 3: Đồ thị của hàm số nào sau đây nhận gốc tọa độ O làm tâm đối xứng s inx A. y . x sinx B. y cosx C. y D. y . x cosx x
Câu 4: Tìm số nghiệm của phương trình 2cos x 1 0
với 0 x 2 3 A. 0 B. 2 C. 3 D. 1
Câu 5: Tìm tất cả các giá trị của x để hàm số y = tanx -1 có nghĩa A. x
k , k B. x
k , k
C. x k 2 , k D. x 2 4
Câu 6: Hàm số y = sinx và y = cosx cùng đồng biến trên khoảng nào sau đây 3 3 A. ; B. ; C. ; 2 D. 0; 2 2 2 2
Câu 7: Tìm tập xác định D của hàm số y cosx
A. D = \ k , k
B. D \ k2 ,k
C. D \ k ,k D. D= 2
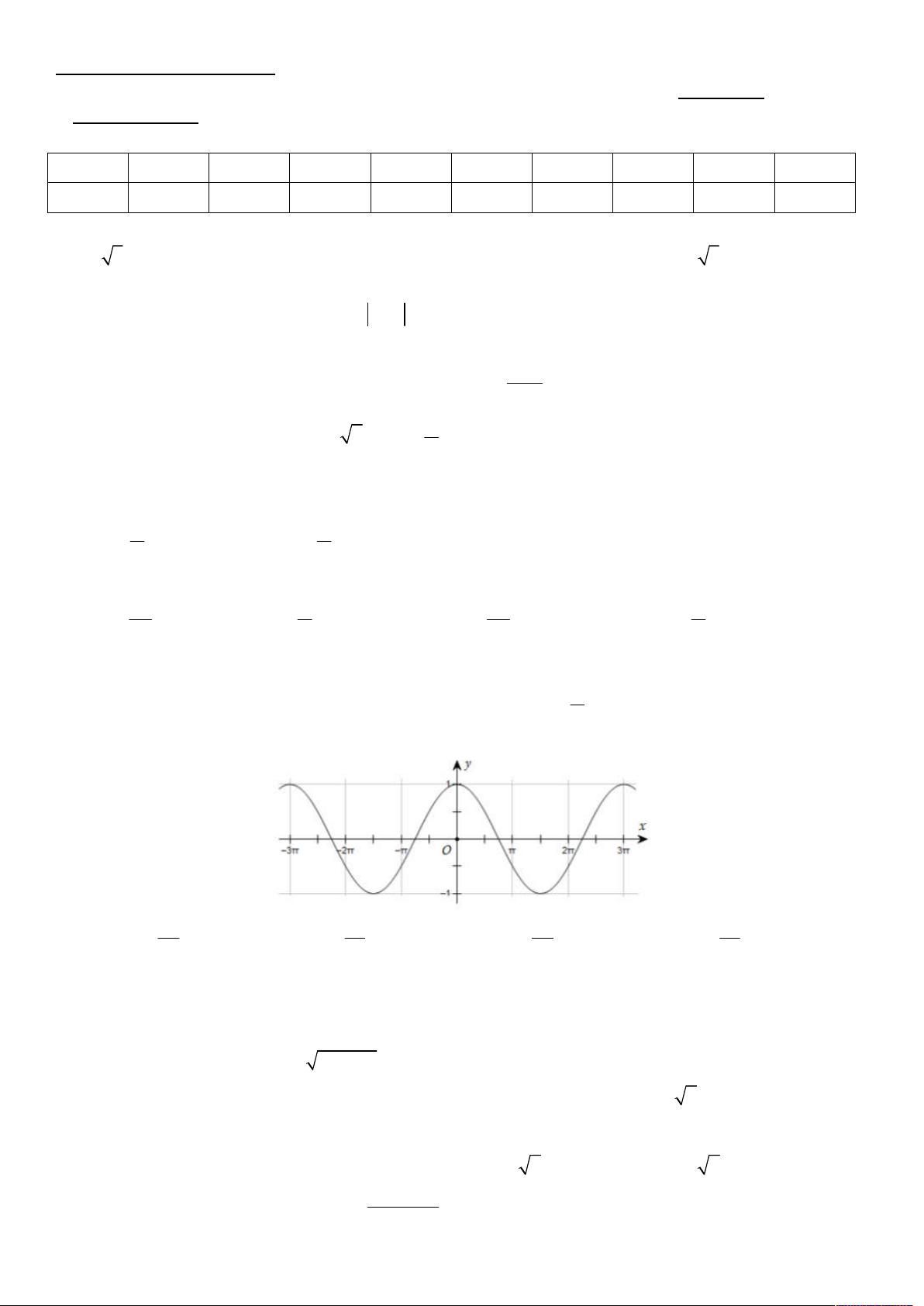
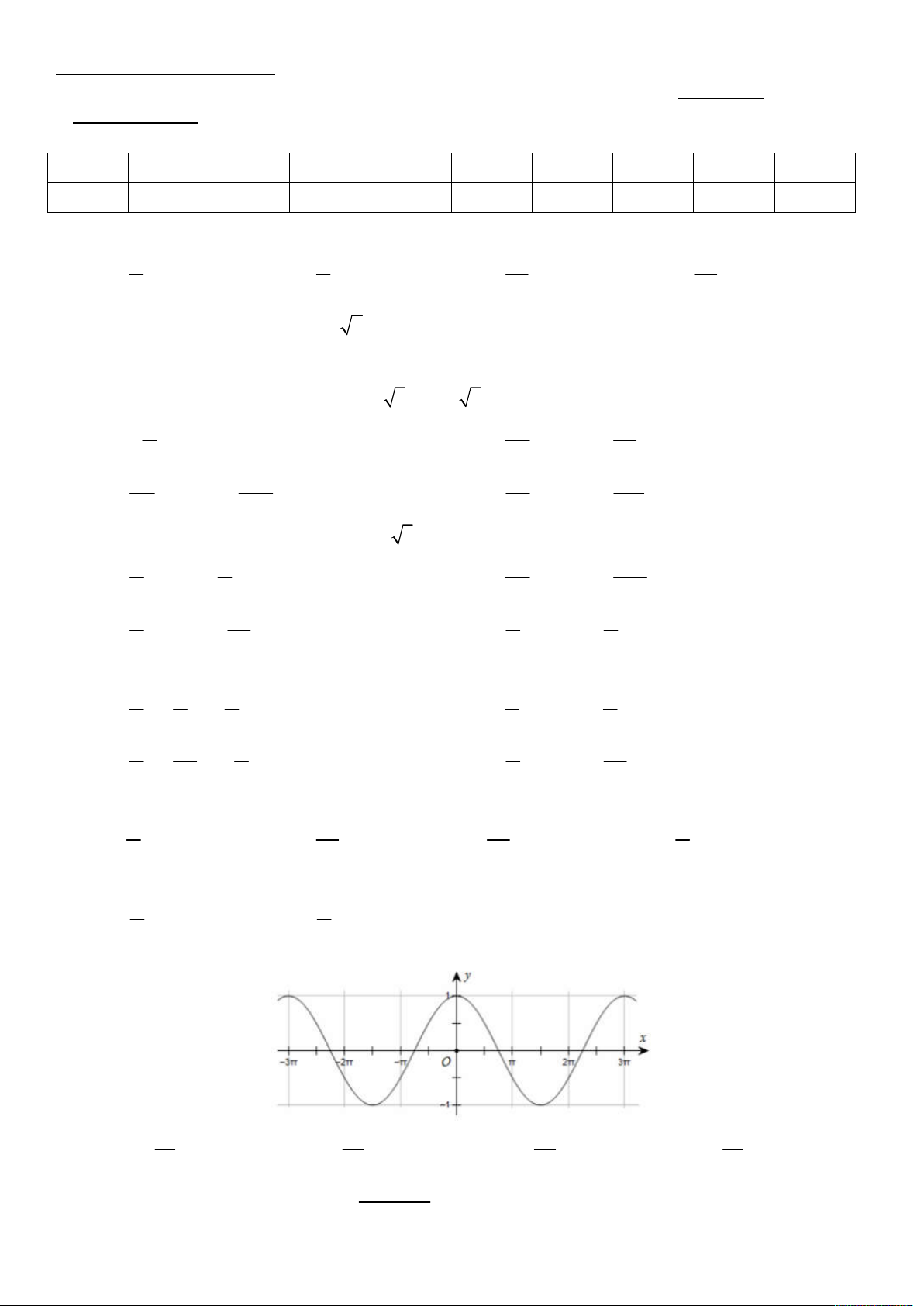
Câu 8: Đường cong trong hình là đồ thị của hàm số nào 2x 3x 2x 3x A. y os c B. y os c C. y sin D. y sin 3 2 3 2
Câu 9: Cho hàm số f (x) sin 3x và 2
g(x) cot x , chọn mệnh đề đúng
A. f(x) là hàm số chẵn, g(x) là hàm lẻ.
B. f(x) là hàm số chẵn, g(x) là hàm chẵn.
C. f(x) là hàm số lẻ, g(x) là hàm lẻ.
D. f(x) là hàm số lẻ, g(x) là hàm chẵn.
Câu 10: Tập giá trị của hàm số y 3 s inx là A. B. 2; 4 C. D. 2; 2
Câu 11: Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y s inx cosx+1 .Tính P = M-m A. P 2 B. P=4 C. P 2 2 D. P 2 1 os c x
Câu 12: Tìm tập xác định D của hàm số y sinx.cosx k
A. D \ {k , k } B. D \{ , k }
C. D \{- k , k }
D. D \{k 2 , k } 2 2
Câu 13: Cho phương trình 4sin5x.sinx – 2cos4x - 3 = 0. Tìm số điểm biểu diễn nghiệm của phương trình lên đường tròn lượng giác A. 6 B. 20 C. 12 D. 3
Câu 14: Tìm tất cả các nghiệm của phương trình 2sinx -1 = 0 x k 2 1 6 A. x
k , k B. s inx C. (k ) D. x k , k 6 3 5 6 2 x k 2 6
Câu 15: Tìm tất cả nghiệm phương trình s inx 3 osx c = 2 5 A. x
k , k B. x
k 2 ; x
k 2 , k 3 12 12 7 7 13 C. x
k 2 ; x
k 2 , k D. x
k 2 ; x
k 2 , k 12 12 12 12
Câu 16: Tìm tất cả các nghiệm của phương trình sin 2x o c sx 2 A. x k ; x
k , k B. x k ; x
k 2 , k 6 2 2 6 3 2 5 C. x
k 2 ; x
k 2 , k D. x
k 2 ; x
k , k 6 6 6 2
Câu 17: Tìm tất cả nghiệm phương trình 2 s in x 3 s inx osx = 1 c 5 A. x k ; x
k , k B. x
k 2 ; x
k 2 , k 2 6 6 6 5 C. x
k 2 ; x
k 2 , k D. x
k 2 ; x
k 2 , k 6 6 2 6
Câu 18: Tìm nghiệm dương nhỏ nhất của phương trình: 2
(2 cos x sinx)(1+sinx) = cos x 3 5 A. x B. x C. x D. x 6 2 3 3
Câu 19: Hàm số y = sin2x đồng biến trên khoảng nào trong các khoảng sau 3 3 A. 0; B. ; C. ; 2 D. ; 4 2 2 2
Câu 20: Tìm tất cả nghiệm phương trình 2 2 2
s in x sin 3x - 2cos 2x = 0 k k A. x k ; x , k
B. x k ; x , k 2 8 2 8 4 k C. x
k , k D. x k ; x , k 2 2 8 4
II) PHẦN TỰ LUẬN (5 ĐIỂM)
Bài 1 (2 điểm): Tìm nghiệm x ; 2
của phương trình: 2 cos x 1 0 3
Bài 2 (3 điểm): Cho phương trình: 2 2
4m .cos 4x cos 4x 3 0 (*)
a) Giải phương trình (*) với m 1
b) Tìm m để phương trình (*) có nghiệm. ----------- HẾT --------- TRƯỜNG THPT NGỌC HỒI
ĐỀ KIỂM TRA ĐẠI SỐ VÀ GIẢI TÍCH 11 – Thời gian 45 phút
Họ và tên học sinh: Lớp: Điểm: MÃ ĐỀ 357
I) TRẮC NGHIỆM (5 ĐIỂM)
Học sinh ghi 1 đáp án lựa chọn vào ô tương ứng trong bảng sau: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Câu 1: Tìm tất cả nghiệm phương trình 2 2 2
s in x sin 3x - 2cos 2x = 0 k k A. x k ; x , k B. x k ; x , k 2 8 2 2 8 4 k
C. x k ; x , k D. x
k , k 8 4 2
Câu 2: Cho hàm số f (x) sin 3x và 2
g(x) cot x , chọn mệnh đề đúng
A. f(x) là hàm số chẵn, g(x) là hàm chẵn.
B. f(x) là hàm số chẵn, g(x) là hàm lẻ.
C. f(x) là hàm số lẻ, g(x) là hàm chẵn.
D. f(x) là hàm số lẻ, g(x) là hàm lẻ.
Câu 3: Hàm số y = sinx và y = cosx cùng đồng biến trên khoảng nào sau đây 3 3 A. 0; B. ; C. ; D. ; 2 2 2 2 2
Câu 4: Đồ thị của hàm số nào sau đây nhận gốc tọa độ O làm tâm đối xứng s inx A. y . x cosx B. y cosx C. y . x sinx D. y x
Câu 5: Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y s inx cosx+1 .Tính P = M-m A. P=4 B. P 2 C. P 2 2 D. P 2
Câu 6: Tìm tập xác định D của hàm số y cosx
A. D = \ k , k
B. D \ k2 ,k
C. D \ k ,k D. D= 2
Câu 7: Đường cong trong hình là đồ thị của hàm số nào 2x 3x 2x 3x A. y os c B. y os c C. y sin D. y sin 3 2 3 2
Câu 8: Tìm tất cả các giá trị của x để hàm số y = tanx -1 có nghĩa A. x
k , k B. x
k , k
C. x k 2 , k D. x 2 4
Câu 9: Cho phương trình 4sin5x.sinx – 2cos4x - 3 = 0. Tìm số điểm biểu diễn nghiệm của phương trình lên đường tròn lượng giác A. 6 B. 20 C. 12 D. 3 1 os c x
Câu 10: Tìm tập xác định D của hàm số y sinx.cosx k
A. D \ {k , k } B. D \{ , k }
C. D \{- k , k }
D. D \{k 2 , k } 2 2
Câu 11: Tìm tất cả nghiệm phương trình s inx 3 osx c = 2 5 A. x
k , k B. x
k 2 ; x
k 2 , k 3 12 12 7 7 13 C. x
k 2 ; x
k 2 , k D. x
k 2 ; x
k 2 , k 12 12 12 12
Câu 12: Trong các hàm số sau đây, hàm số nào là hàm số chẵn
A. y tan2x cot x B. y s inx.cos2x C. y s inx+1 D. 2 y o
c s x s inx 2
Câu 13: Tìm tất cả các nghiệm của phương trình 2sinx -1 = 0 x k 2 1 6 A. x
k , k B. s inx C.
(k ) D. x k , k 6 3 5 6 2 x k 2 6
Câu 14: Tìm số nghiệm của phương trình 2cos x 1 0
với 0 x 2 3 A. 0 B. 1 C. 2 D. 3
Câu 15: Tìm tất cả các nghiệm của phương trình sin 2x o c sx 2 A. x k ; x
k , k B. x k ; x
k 2 , k 6 2 2 6 3 2 5 C. x
k 2 ; x
k 2 , k D. x
k 2 ; x
k , k 6 6 6 2
Câu 16: Tìm tất cả nghiệm phương trình 2 s in x 3 s inx osx = 1 c 5 A. x k ; x
k , k B. x
k 2 ; x
k 2 , k 2 6 6 6 5 C. x
k 2 ; x
k 2 , k D. x
k 2 ; x
k 2 , k 6 6 2 6
Câu 17: Tìm nghiệm dương nhỏ nhất của phương trình: 2
(2 cos x sinx)(1+sinx) = cos x 3 5 A. x B. x C. x D. x 6 3 2 3
Câu 18: Hàm số y = sin2x đồng biến trên khoảng nào trong các khoảng sau 3 3 A. 0; B. ; C. ; 2 D. ; 4 2 2 2
Câu 19: Phương trình nào sau đây vô nghiệm A. s inx o
c s2018 B. 4s inx 3 o
c sx = -5 C. 3 s inx osx = - c 2 D. 3 s in2x os2x = - c 3
Câu 20: Tập giá trị của hàm số y 3 s inx là A. 2; 4 B. C. 2; 2 D.
II) PHẦN TỰ LUẬN (5 ĐIỂM)
Bài 1 (2 điểm): Tìm nghiệm x (
;5 ) của phương trình: tan(x ) 1 0 4
Bài 2 (3 điểm): Cho phương trình: 2
3sin 2x 4m sin 2x 4 0 (*) 1
a) Giải phương trình (*) với m 4
b) Tìm m để phương trình (*) có nghiệm. ----------- HẾT --------- TRƯỜNG THPT NGỌC HỒI
ĐỀ KIỂM TRA ĐẠI SỐ VÀ GIẢI TÍCH 11 – Thời gian 45 phút
Họ và tên học sinh: Lớp: Điểm: MÃ ĐỀ 485
I) TRẮC NGHIỆM (5 ĐIỂM)
Học sinh ghi 1 đáp án lựa chọn vào ô tương ứng trong bảng sau: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Câu 1: Tìm nghiệm dương nhỏ nhất của phương trình: 2
(2 cos x sinx)(1+sinx) = cos x 3 5 A. x B. x C. x D. x 6 3 2 3
Câu 2: Tìm số nghiệm của phương trình 2cos x 1 0
với 0 x 2 3 A. 0 B. 1 C. 2 D. 3
Câu 3: Tìm tất cả nghiệm phương trình s inx 3 osx c = 2 5 A. x
k , k B. x
k 2 ; x
k 2 , k 3 12 12 7 7 13 C. x
k 2 ; x
k 2 , k D. x
k 2 ; x
k 2 , k 12 12 12 12
Câu 4: Tìm tất cả nghiệm phương trình 2 s in x 3 s inx osx = 1 c 5 A. x k ; x
k , k B. x
k 2 ; x
k 2 , k 2 6 6 6 5 C. x
k 2 ; x
k 2 , k D. x
k 2 ; x
k 2 , k 6 6 2 6
Câu 5: Tìm tất cả các nghiệm của phương trình sin 2x o c sx A. x k ; x
k , k B. x
k 2 ; x
k , k 6 2 2 6 2 2 5 C. x k ; x
k 2 , k D. x
k 2 ; x
k 2 , k 6 3 2 6 6
Câu 6: Hàm số y = sin2x đồng biến trên khoảng nào trong các khoảng sau 3 3 A. 0; B. ; C. ; 2 D. ; 4 2 2 2
Câu 7: Tìm tất cả các giá trị của x để hàm số y = tanx -1 có nghĩa A. x
k , k B. x
k , k
C. x k 2 , k D. x 2 4
Câu 8: Đường cong trong hình là đồ thị của hàm số nào 3x 2x 2x 3x A. y sin B. y sin C. y os c D. y os c 2 3 3 2 1 os c x
Câu 9: Tìm tập xác định D của hàm số y sinx.cosx k
A. D \ {k , k } B. D \{ , k }
C. D \{- k , k }
D. D \{k 2 , k } 2 2
Câu 10: Trong các hàm số sau đây, hàm số nào là hàm số chẵn
A. y s inx+1 B. y s inx.cos2x C. y tan2x cot x D. 2 y o
c s x s inx 2
Câu 11: Đồ thị của hàm số nào sau đây nhận gốc tọa độ O làm tâm đối xứng s inx A. y . x cosx B. y cosx C. y . x sinx D. y x
Câu 12: Tìm tất cả các nghiệm của phương trình 2sinx -1 = 0 x k 2 6 1 A. x
k , k B. x k , k C. (k ) D. s inx 6 6 2 5 3 x k 2 6
Câu 13: Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y s inx cosx+1 .Tính P = M-m A. P 2 B. P 2 C. P=4 D. P 2 2
Câu 14: Hàm số y = sinx và y = cosx cùng đồng biến trên khoảng nào sau đây 3 3 A. 0; B. ; C. ; D. ; 2 2 2 2 2
Câu 15: Cho phương trình 4sin5x.sinx – 2cos4x - 3 = 0. Tìm số điểm biểu diễn nghiệm của phương trình lên đường tròn lượng giác A. 6 B. 12 C. 3 D. 20
Câu 16: Cho hàm số f (x) sin 3x và 2
g(x) cot x , chọn mệnh đề đúng
A. f(x) là hàm số lẻ, g(x) là hàm lẻ.
B. f(x) là hàm số lẻ, g(x) là hàm chẵn.
C. f(x) là hàm số chẵn, g(x) là hàm lẻ.
D. f(x) là hàm số chẵn, g(x) là hàm chẵn.
Câu 17: Tìm tập xác định D của hàm số y cosx
A. D= B. D \ k 2 , k
C. D = \k , k
D. D \ k ,k 2
Câu 18: Phương trình nào sau đây vô nghiệm A. s inx o
c s2018 B. 4s inx 3 o
c sx = -5 C. 3 s inx osx = - c 2 D. 3 s in2x os2x = - c 3
Câu 19: Tập giá trị của hàm số y 3 s inx là A. 2; 4 B. 2; 2 C. D.
Câu 20: Tìm tất cả nghiệm phương trình 2 2 2
s in x sin 3x - 2cos 2x = 0 k k A. x k ; x , k
B. x k ; x , k 2 8 2 8 4 k C. x k ; x , k D. x
k , k 2 8 4 2
II) PHẦN TỰ LUẬN (5 ĐIỂM)
Bài 1 (2 điểm): Tìm nghiệm x ; 2
của phương trình: 2 cos x 1 0 3
Bài 2 (3 điểm): Cho phương trình: 2 2
4m .cos 4x cos 4x 3 0 (*)
a) Giải phương trình (*) với m 1
b) Tìm m để phương trình (*) có nghiệm.
----------------------------------------------- ----------- HẾT ----------
ĐÁP ÁN KIỂM TRA 1 TIẾT LƯỢNG GIÁC 11 – BÀI SỐ 2
I) TRẮC NGHIỆM (5 ĐIỂM) Đáp án Câu Đáp án 132 Đáp án 209 Đáp án 485 357 1 C D B B 2 B B C C 3 C D D B 4 C B A A 5 D A C C 6 A C D A 7 D D A A 8 A A A C 9 B D C B 10 A D B D 11 B C B A 12 C B D C 13 D C C D 14 A C C D 15 B B B B 16 D B A B 17 B A B A 18 C C A D 19 C A D B 20 D D C C
II) ĐÁP ÁN TỰ LUẬN (5 ĐIỂM) ĐỀ 132+357 BÀI ĐÁP ÁN ĐIỂM 1
Tìm nghiệm x (
;5 ) của phương trình: tan(x ) 1 0 ( 2điểm) 4 0,5 tan(x ) 1 0 x
k x k 4 4 4 0,5x2 Vì x ( ;5 ) nên
k 5 1 k 5(k ) k 0;1; 2;3; 4 0,5
x 0; x ; x 2 ; x 3 ; x 4 Câu 2 Cho phương trình: 2
3sin 2x 4m sin 2x 4 0 (*) 1
a) Giải phương trình (*) với m 4 2
3sin 2x sin 2x 4 0( 1 sin 2x 1) 0,5 a(2 0,5x2 điểm) sin 2x 1 4
sin 2x (KTM ) 0,5 3
Với sin2x = 1 x
k , (k ) 4 Vậy:…
b) Tìm m để phương trình (*) có nghiệm. Đặt sin 2x = t ( 2
1 t 1) f (t) 3t 4mt 4 0 (1) 0,25 0,25 Tìm 0, m
pt (1) luôn có 2 nghiệm trái dấu với mọi m b)1 điểm
nên pt (1) vô nghiệm khi 2 nghiệm t ;t thỏa mãn t 1 1 t 1 2 1 2 f (1) 0 4 m 1 0 1 0,25 m f (1) 0 4m 1 0 4 1 0,25
Vậy để pt (*) có nghiệm thì |m| > 4 ĐỀ 209+485 BÀI ĐÁP ÁN ĐIỂM 1 Tìm nghiệm x
; 2 của phương trình: 2 cos x 1 0 ( 3 2điểm) 0,5
2 cos x 1 0 x k 2 3 0,5x2 x ; 2
k 2 2 k 0 3 3 3 0,5 x ; 2
k 2 2 k 0,1 3 3 3 5 x ; x 3 3 Câu 2 Cho phương trình: 2 2
4m .cos 4x cos 4x 3 0 (*)
Giải phương trình (*) với m 1 cos4x=1 2
4cos 4x cos 4x 3 0 3 a(2 cos4x= 0,5 4 điểm) k Cos 4x=1 x 0,5x2 2 3 1 3 k Cos4x = x arccos( ) 0,5 4 4 4 2
b) Tìm m để phương trình (*) có nghiệm. Đặt cos 4x = t ( 2 2
1 t 1) f (t) 4m t t 3 0 (1) 0,25
+) m=0 thì (1) t 3 pt (1) vô nghiệm b)1 0,25
+)m 0 0 pt (1) luôn có 2 nghiệm trái dấu điểm
nên pt (1) vô nghiệm khi 2 nghiệm t ;t thỏa mãn t 1 1 t 1 2 1 2 2 f (1) 0 4m 2 0 2 0,25 m
và m 0 Vậy để pt (*) có nghiệm thì |m| > 2 f (1) 0 4m 4 0 2 0,25 2 2




