Đề kiểm tra Đại số và Giải tích 11 chương 1 trường THPT Thừa Lưu – TT. Huế

Đề kiểm tra Đại số và Giải tích 11 chương 1 trường THPT Thừa Lưu – TT. Huế gồm 2 mã đề, mỗi mã đề gồm 4 câu hỏi tự luận

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

6 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
THPT THỪA LƯU – T.T.HUẾ
KIỂM TRA 1 TIẾT – CHƯƠNG I
ĐẠI SỐ 11CB
ĐỀ 1
Câu 1. (2,0 điểm) Tìm tập xác định các hàm số sau:
a)
1 sin
cos 1
x
y
x
b)
sin cos2
cot 3
xx
y
x
Câu 2. (2,0 điểm) Giải các phương trình sau:
a)
0
3
tan 3 30
3
x
b)
2cos 3 2 0
6
x



Câu 3. (3,0 điểm) Giải các phương trình sau:
a)
2
cos 3sin 3 0xx
b)
3sin3 os3 2sin2x c x x
Câu 4. (3,0 điểm) Giải các phương trình sau:
a)
2sin cos sin2 1 0x x x
b)
KIỂM TRA 1 TIẾT – CHƯƠNG I
ĐẠI SỐ 11CB
ĐỀ 2
Câu 1. (2,0 điểm) Tìm tập xác định các hàm số sau:
a)
tan 3
3
yx




b)
os2x-1
1 2sin2x
c
y
Câu 2. (2,0 điểm) Giải các phương trình sau:
a)
0
cot 3 60 3x
b)
2cos2 3 0x 
Câu 3. (3,0 điểm) Giải các phương trình sau:
a)
2
2sin 5 os 5x c x
b)
3 os3 sin3 2cos2c x x x
Câu 4. (3,0 điểm) Giải các phương trình sau:
a) sin6x + sin2x +2sin
2
x =1
b)
1 sinx cos sin2 os2
0
tan2
x x c x
x
THPT THỪA LƯU – T.T.HUẾ
ĐÁP ÁN KIỂM TRA ĐẠI SỐ 11CB CHƯƠNG 1
ĐỀ 1
CÂU
BÀI GIẢI
ĐIỂM
1
a
(1,0)
Hàm số xác định
cos 1 0x
cos 1x
2,x k k
Vậy tập xác định của hàm số :
\ 2 ,D k k

.
0,5
0,5
b
(1,0)
Hàm số
sin cos2
cot 3
xx
y
x
xác định khi
sin 0
cot 3 0
x
x

sin 0
cot 3
6
x k k
x
x
x k k




Z
Z
Vậy tập xác định của hàm số trên là:
\ , ,
6
D k k k k






ZZ
0,5
0,5
2
a
(1,0)
0 0 0
0 0 0 0 0
3
tan 3 30 tan 3 30 tan 30
3
3 30 30 180 3 180 60 , .
xx
x k x k x k k
0,5
0,5
b
(1,0)
23
cos 3 cos 3 cos
6 2 6 4
3 11 2
32
6 4 36 3
3 7 2
32
6 4 36 3
pt x x
x k x k
x k x k







,
k
0,5
0,5
THPT THỪA LƯU – T.T.HUẾ
3
a
(1,5)
22
2
cos 3sin 3 0 1 sin 3sin 3 0
sin 1
sin 3sin 2 0
sin 2
2 , .
2
pt x x x x
x
xx
x vn
x k k
0,5
0,5
0,5
b
(1,5)
3sin3 os3 2sin 2
31
sin3 os3 sin2
22
cos sin3 sin os3 sin 2
66
sin 3 sin 2
6
3 2 2 2
66
72
3 2 2
6 30 3
x c x x
x c x x
x c x x
xx
x x k x k
kZ
k
x x k x















0,5
0,5
0,5
4
a
(1,5)
Phương trình
2sin 1 1 cos 0xx
.
2sin 1 0
1 cos 0
x
x


1
sin
2
cos 1
x
x
2
6
5
2
6
2
xk
xk
xk

,
k
0,5
0,5
0,5
b
(1,5)
22
)
21
sin 4 cos 6 sin 10
2
c x x x



1 cos8 1 cos12
sin 10 10
2 2 2
xx
x




cos12 cos8 2sin 10
2
2cos10 .cos2 2cos10
2cos10 cos2 1 0
cos10 0
cos2 1
x x x
x x x
xx
x
x




0,5
0,5
THPT THỪA LƯU – T.T.HUẾ
.cos10 0 10 ,
2 20 10
.cos2 1 2 2 ,
2
x x k x k k
x x k x k k
Vậy phương trình có các nghiệm là
20 10
xk


và
()
2
x k k
Z
…
0,5
ĐỀ 2
CÂU
BÀI GIẢI
ĐIỂM
1
a
(1,0)
HSXĐ
os 3 0
3
3
32
5
3
6
5
18 3
cx
xk
xk
xk






5
\
18 3
k
D R k Z




.
0,5
0,5
b
(1,0)
1 2sin 2x 0
1
sin 2
2
22
6
7
22
6
12
7
12
x
xk
xk
xk
xk






Vậy tập xác định của hàm số trên là:
7
\,
12 12
D R k k k Z





0,5
0,5
THPT THỪA LƯU – T.T.HUẾ
2
a
(1,0)
0
00
0 0 0
00
00
cot 3 60 3
cot 3 60 cot( 30 )
3 60 30 180
3 90 180
30 60
x
x
xk
xk
xk
0,5
0,5
b
(1,0)
35
2cos2 3 0 os2 os2 os
26
5
5
22
6
12
55
22
6 12
x c x c x c
xk
xk
kZ
x k x k





0,5
0,5
3
a
(1,5)
2
2
2
2sin 5 os 5
2 1 os 5cos 5 0
2 os 5cos 3 0
os 1
3
os
2
2
x c x
c x x
c x x
cx
cx
xk


0,5
0,5
0,5
b
(1,5)
3 os3 sin3 2cos2
31
os3 sin3 cos2
22
cos os3 sin sin3 cos2
66
cos 3 cos2
6
3 2 2 2
66
2
3 2 2
6 30 3
c x x x
c x x x
c x x x
xx
x x k x k
kZ
k
x x k x














0,5
0,5
0,5
2sin4xcos2x-(1-2sin
2
x) = 1
0,5
THPT THỪA LƯU – T.T.HUẾ
4
a
(1,5)
2sin2xcos2x- cos2x = 0
cos2x(2sin2x-1) = 0
20
1
sin 2
2
cos x
x
42
12
5
12
k
x
xk
xk




0,5
0,5
b
(1,5)
2
4
:1 sinx cos sin2 os2 0 1 sinx 2sin cos cos 2cos 1 0
sinx 1 2cos cos 1 2cos 0 1 2cos sinx cos 0
2
1
2
1 2cos 0
cos
2
3
2
2
sinx cos 0
3
tanx 1
4
xk
pttt x x c x x x x x
x x x x x
xk
x
x
xk
x
xk







0,5
0,5
0,5
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

THPT THỪA LƯU – T.T.HUẾ
KIỂM TRA 1 TIẾT – CHƯƠNG I ĐẠI SỐ 11CB ĐỀ 1
Câu 1. (2,0 điểm) Tìm tập xác định các hàm số sau: 1 sin x sin x  cos 2x a) y y  cos x b) 1 cot x  3
Câu 2. (2,0 điểm) Giải các phương trình sau:    0 3      a) tan 3x  30  b) 2cos 3x 2 0   3  6 
Câu 3. (3,0 điểm) Giải các phương trình sau: a) 2
cos x  3sin x  3  0 b) 3sin3x  o
c s3x  2sin 2x
Câu 4. (3,0 điểm) Giải các phương trình sau:
a) 2sin x  cos x  sin 2x 1  0    b) 2 2 21
sin 4x  cos 6x  sin 10x     2 
KIỂM TRA 1 TIẾT – CHƯƠNG I ĐẠI SỐ 11CB ĐỀ 2
Câu 1. (2,0 điểm) Tìm tập xác định các hàm số sau:    o c s2x-1
a) y  tan 3x    y   3  b) 1 2s in2x
Câu 2. (2,0 điểm) Giải các phương trình sau: 0
a) cot 3x  60    3 b) 2 cos 2x  3  0
Câu 3. (3,0 điểm) Giải các phương trình sau: a) 2 2sin x  5 o c sx  5 b) 3 o
c s3x  sin 3x  2 cos 2x
Câu 4. (3,0 điểm) Giải các phương trình sau: a) sin6x + sin2x +2sin 2x =1     b) 1 s inx cos x sin 2x o c s2x  0 tan 2x
THPT THỪA LƯU – T.T.HUẾ
ĐÁP ÁN KIỂM TRA ĐẠI SỐ 11CB CHƯƠNG 1 ĐỀ 1 CÂU BÀI GIẢI ĐIỂM
Hàm số xác định  cos x 1 0 0,5 a  cos x  1
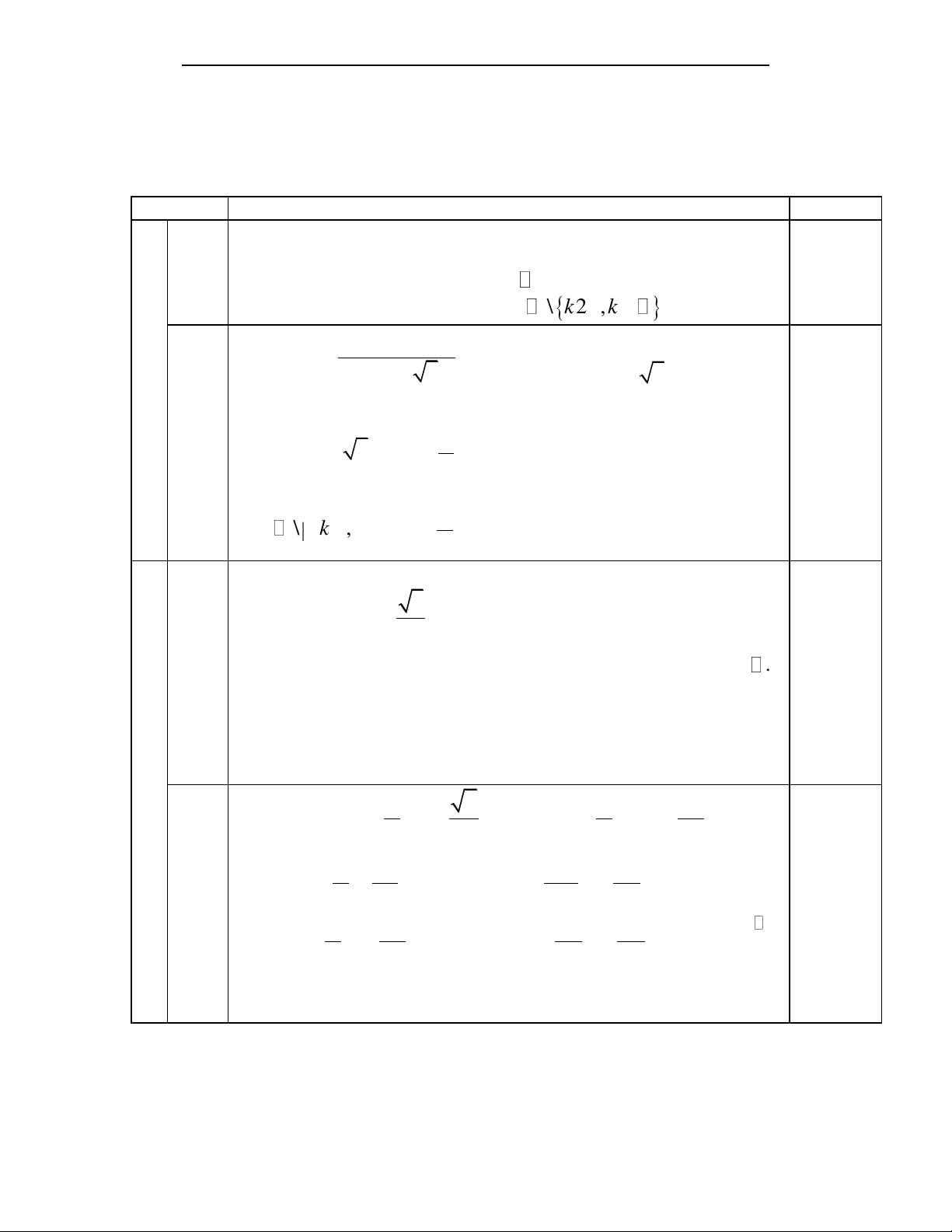
(1,0)  x k2,k
Vậy tập xác định của hàm số : D
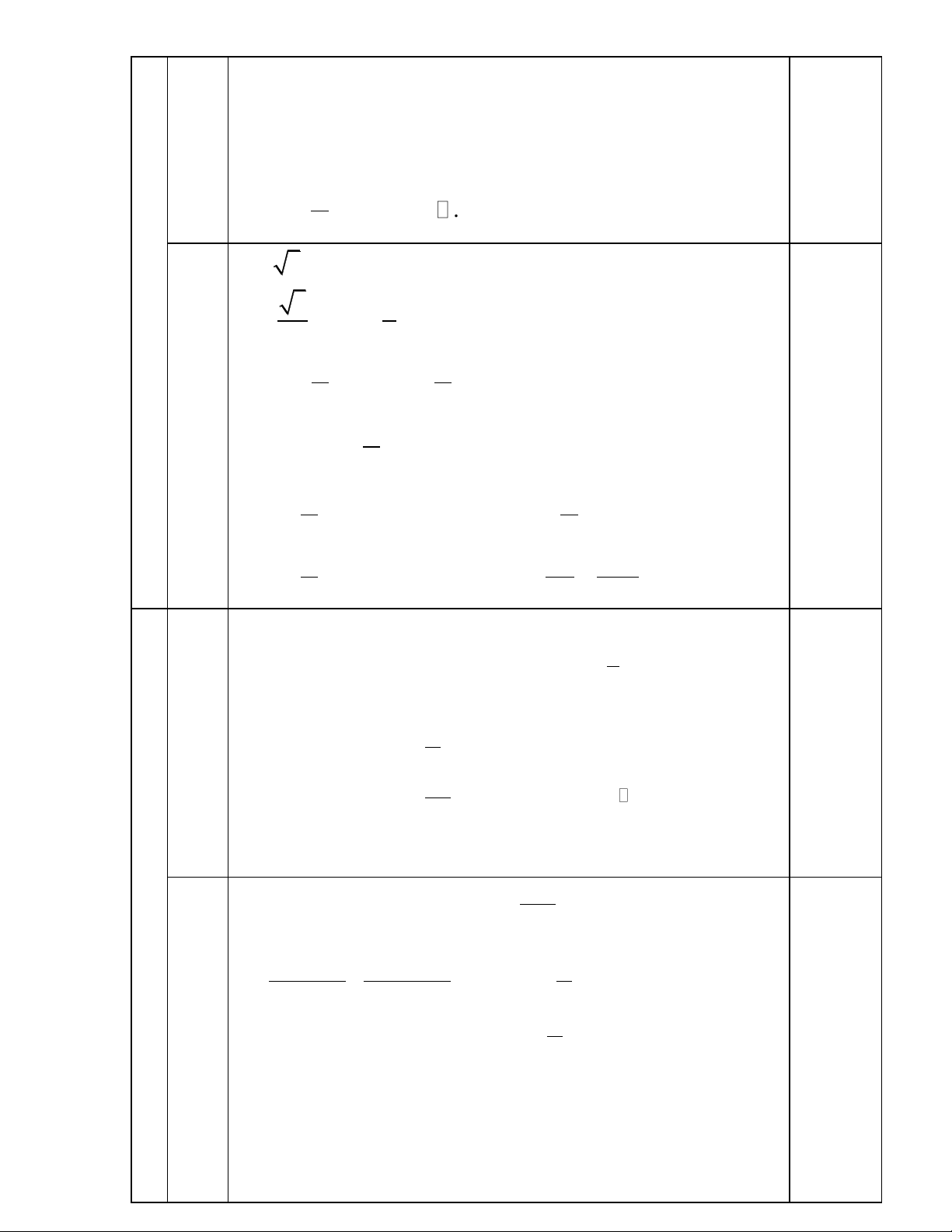
\ k2 ,k   . 0,5   x x s  in x 0 Hàm số sin cos 2 y   0,5 1 cot x  xác định khi 3 cot x 3 0 b (1,0)
xk k Z s  in x0      cot x  3
x   k k Z  6
Vậy tập xác định của hàm số trên là:    D
\ k ,k  Z  
k ,kZ 0,5   6  3 0 0 0 a
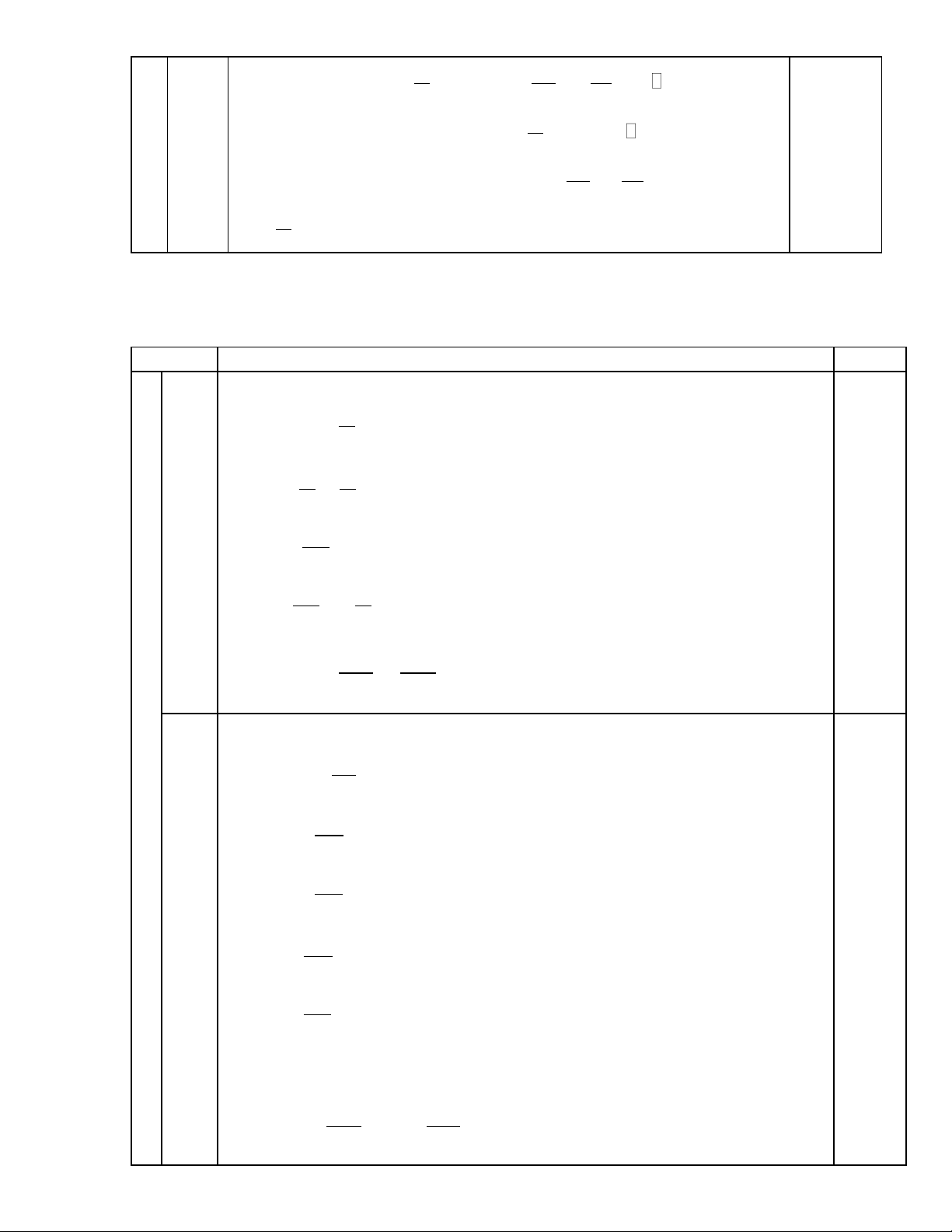
tan 3x  30   
 tan 3x 30   tan 3  0  0,5 (1,0) 3 0 0 0 0 0  3x  30  3  0  1
k 80  3x  1
k 80  x k60 , k  . 0,5 2    2    3
pt  cos 3x     cos 3x   cos     0,5  6  2  6  4   3  11 2       b 3x k 2 x k   6 4 36 3 (1,0)     0,5   3 7   2 , k  3x     k2 x    k   6 4  36 3
THPT THỪA LƯU – T.T.HUẾ 2 2
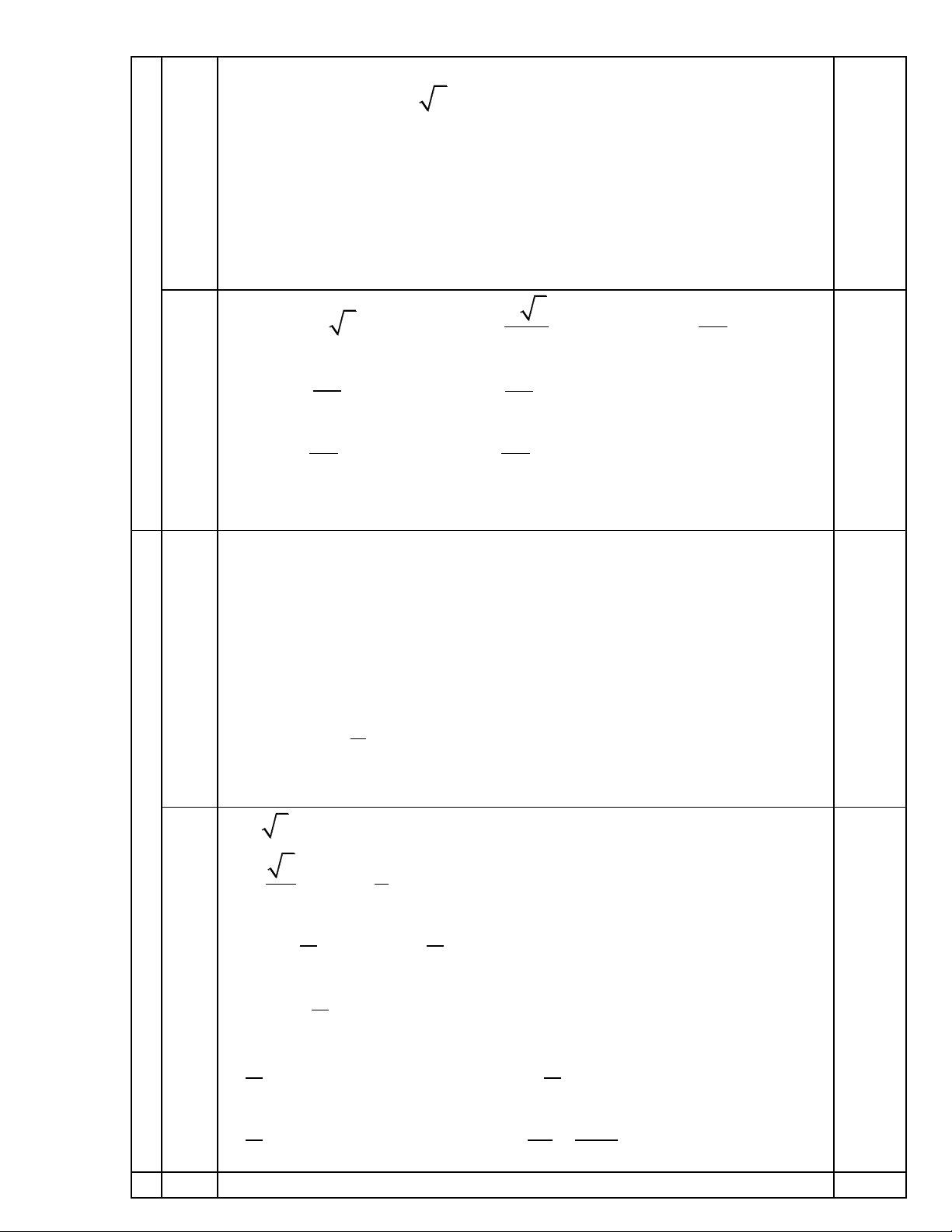
pt  cos x  3sin x  3  0  1 sin x  3sin x  3  0 0,5 a  sin x 1 2
(1,5)   sin x  3sin x  2  0   sin x  2  vn 0,5
x   k2 ,k  . 3 2 0,5 3sin3x  o
c s3x  2 sin 2x 0,5 3 1    b sin3x o c s3x sin 2x 2 2 (1,5)    cos sin3x  sin o
c s3x  sin 2x 6 6 0,5     sin 3x   sin 2x    6      3x   2x k2 x   k2   6 6    k Z  7 k 2   0,5 3x
   2x k2 x    6  30 3
Phương trình  2sin x  
1 1 cos x  0 . 0,5  1 2sin x 1  0 sin x  0,5     2 1   cos x  0  cos x 1 a   x   k2  (1,5) 6   5 0,5  x
k2 , k   6 4 x k2      2 2 21
c sin 4x  cos 6x  sin 10x  )    2  b
1cos8x 1 cos12x    (1,5)   sin 10x 10    0,5 2 2  2      
cos12x  cos8x  2sin 10x     2   2  cos10 .
x cos 2x  2cos10x
2cos10x cos 2x   1 0 cos10x 0   cos 2x 1 0,5
THPT THỪA LƯU – T.T.HUẾ   
.cos10x  0 10x
k  x  k , k  2 20 10 
.cos 2x  1 2x   k2  x   k,k  2  
Vậy phương trình có các nghiệm là x  k và 20 10  0,5 x
k (k  ) Z … 2 ĐỀ 2 CÂU BÀI GIẢI ĐIỂM HSXĐ 0,5 a    (1,0) os c 3x   0    3     3x    k 3 2 1 5  3x   k 6 0,5 5   x   k 18 3 5 k  D R \    k Z 18 3  . 1 2 sin 2x  0 0,5 1  b  sin 2x  (1,0) 2    2x   k2  6   7 2x   k2  6 0,5    x   k  12   7 x   k  12
Vậy tập xác định của hàm số trên là:    7  D R \   k ,  k  k Z  12 12 
THPT THỪA LƯU – T.T.HUẾ cot  0 3x  60    3 a 0,5 (1,0)  cot  0 3x  60  0  cot( 3  0 ) 0 0 0  3x  60  3  0  1 k 80 2 0,5 0 0  3x  9  0  1 k 80 0 0  x  3  0  k60  3 5
2 cos 2x  3  0  o c s2x   o c s2x  o c s 0,5 2 6  5  5 b 2x   k2 x   k   6 12 (1,0)    k Z 0,5 5 5   2x    k2 x    k  6  12 2 2 sin x  5 o c sx  5 0,5 a  2 2 1 o
c s x  5cos x  5  0 (1,5) 2  2  o
c s x  5 cos x  3  0 0,5  o c sx  1 3   0,5 3  os c x  2    x k 2 3 os3 c
x  sin 3x  2 cos 2x 0,5 3 1    b os3 c x sin 3x cos 2x 2 2 (1,5)    cos os3 c x  sin
sin 3x  cos 2x 6 6 0,5     cos
 3x  cos 2x    6    
 3x  2x k2 x    k2   6 6    k Z   k 2   0,5  3x  2  x k2 x     6  30 3 2sin4xcos2x-(1-2sin 2x) = 1 0,5
THPT THỪA LƯU – T.T.HUẾ 2sin2xcos2x- cos2x = 0 cos2x(2sin2x-1) = 0 0,5 cos2x  0  1 a sin 2x   2 (1,5)   k   4 x  4 2 0,5  
x   k  12  5 x   k  12    x k    4  0,5 2
pttt :1 s inx  cos x  sin 2x  o
c s2x  0  1 s inx  2sin x cos x  cos x  2 cos x 1  0 b
 sinx 1 2cos x  cos x1 2cos x  0  1 2cos xsinx  cos x  0 0,5 (1,5)  2  1 x    k2 1   2cos x  0 cos x     3 2    2    x    k2 sinx  cos x  0   3  t anx  1  x    k  4 0,5