Đề kiểm tra Đại số và Giải tích 11 chương 2 trường THPT Thị Xã Quảng Trị

Đề kiểm tra Đại số và Giải tích 11 chương 2 trường THPT Thị Xã Quảng Trị gồm 4 mã đề, mỗi mã đề gồm 5 bài toán tự luận, thời gian làm bài 45 phút, đề kiểm tra có lời giải chi tiết.

21 11 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

7 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
TRƯỜNG THPT TX QUẢNG TRỊ KIỂM TRA MỘT TIẾT TOÁN 11 NC
Tổ Toán Môn: ĐS-GT. ĐỀ SỐ :1 (Khối sáng)
Câu 1 (3 điểm): Cho
9,8,6,5,2,1A
a) Từ A lập được bao nhiêu số có 5 chữ số đôi một khác nhau
b) Từ A lập được bao nhiêu số lẽ có 4 chữ số đôi một khác nhau
Câu 2 (1,5 điểm): Giải phương trình:
xCA
x
xx
14
23
(với
x
là số nguyên dương)
Câu 3 (1,5 điểm): Tìm hệ số của
4
x
trong khai triển biểu thức
8
2
2
1
x
x
(với
0x
).
Câu 4 (2 điểm): Cho
120,119,...,3,2,1C
. Chọn ngẫu nhiên 2 số từ C. Tính xác suất để chọn được 2 số có tích
chia hết cho 7
Câu 5 (2 điểm):
a) Có 2 giá sách. Giá I có: 5 sách Toán, 6 sách Lý. Giá II có: 4 sách Toán, 8 sách Lý. Ở mỗi giá các cuốn
sách cùng môn đôi một khác nhau. Từ mỗi giá chọn ngẫu nhiên 1 cuốn sách. Tính xác suất để chọn được 2
cuốn sách khác môn.
b) Một nhóm có 20 học sinh trong đó có 9 nam và 11 nữ. Chọn ngẫu nhiên 8 học sinh. Tính xác suất để trong 8
học sinh chọn được luôn có không quá 6 nữ.
TRƯỜNG THPT TX QUẢNG TRỊ KIỂM TRA MỘT TIẾT TOÁN 11 NC
Tổ Toán Môn: ĐS-GT. ĐỀ SỐ : 2 (Khối sáng)
Câu 1 (3 điểm): Cho
9,7,6,5,3,2,1B
a) Từ B lập được bao nhiêu số có 6 chữ số đôi một khác nhau
b) Từ B lập được bao nhiêu số chẵn có 4 chữ số đôi một khác nhau
Câu 2 (1,5 điểm): Giải phương trình:
xCA
xx
162
23
(với
x
là số nguyên dương)
Câu 3 (1,5 điểm): Tìm số hạng không chứa
x
trong khai triển biểu thức
9
2
2
1
x
x
(với
0x
).
Câu 4 (2 điểm): Cho
. Chọn ngẫu nhiên 2 số từ D. Tính xác suất để chọn được 2 số có tích chia
hết cho 7
Câu 5 (2 điểm):
a) Có 2 giá sách: Giá I có: 4 sách Toán, 6 sách Lý. Giá II có: 5 sách Toán, 6 sách Lý. Ở mỗi giá các cuốn sách
cùng môn đôi một khác nhau. Từ mỗi giá chọn ngẫu nhiên 1 cuốn sách. Tính xác suất để chọn được 2 cuốn sách
cùng môn.
b) Một nhóm có 18 học sinh trong đó có 8 nam và 10 nữ. Chọn ngẫu nhiên 7 học sinh. Tính xác suất để trong 7 học
sinh chọn được luôn có không quá 5 nữ.
TRƯỜNG THPT TX QUẢNG TRỊ KIỂM TRA MỘT TIẾT TOÁN 11 NC
Tổ Toán Môn: ĐS-GT. ĐỀ SỐ : 1 (Khối chiều)
Câu 1 (3 điểm): Cho
8,7,6,5,1E
a) Từ E lập được bao nhiêu số có 4 chữ số đôi một khác nhau
b) Từ E lập được bao nhiêu số có 3 chữ số đôi một khác nhau và chia hết cho 5
Câu 2 (1,5 điểm): Giải phương trình:
10
6
2
1
322
2
x
xxx
C
x
AA
(với
x
là số nguyên dương)
Câu 3 (1,5 điểm): Tìm số hạng chứa
7
x
trong khai triển biểu thức
8
2
2
x
x
(với
0x
).
Câu 4 (2 điểm): Cho
19,18,...,3,2,1S
. Chọn ngẫu nhiên 5 số từ S. Tính xác suất để chọn được 5 số có tổng chia
hết cho 2
Câu 5 (2 điểm): Có 2 hộp . Hộp I có: 5 bi màu đỏ, 7 bi màu xanh. Hộp II có: 4 bi màu đỏ, 6 bi màu xanh. Ở mỗi
hộp các bi cùng màu đôi một khác nhau.
a) Từ hộp I lấy ngẫu nhiên ra 2 bi, tiếp đó từ hộp II lấy ngẫu nhiên ra 1 bi. Tính xác suất để trong 3 bi lấy được
có đúng 2 bi đỏ và 1 bi xanh
b) Xếp ngẫu nhiên 12 bi ở hộp I thành một hàng ngang. Tính xác suất để có ít nhất hai bi đỏ xếp cạnh nhau
TRƯỜNG THPT TX QUẢNG TRỊ KIỂM TRA MỘT TIẾT TOÁN 11 NC
Tổ Toán Môn: ĐS-GT. ĐỀ SỐ : 2 (Khối chiều)
Câu 1 (3 điểm): Cho
9,6,5,4,2,1F
a) Từ F lập được bao nhiêu số có 3 chữ số đôi một khác nhau
b) Từ F lập được bao nhiêu số có 4 chữ số đôi một khác nhau và không chia hết cho 5
Câu 2 (1,5 điểm): Giải phương trình:
28
2
112
2
2
23
xx
x
x
AAC
x
(với
x
là số nguyên dương)
Câu 3 (1,5 điểm): Tìm số hạng chứa
8
x
trong khai triển biểu thức
10
2
2
x
x
(với
0x
).
Câu 4 (2 điểm): Cho
25,24,...,3,2,1T
. Chọn ngẫu nhiên 5 số từ T. Tính xác suất để chọn được 5 số có tổng
không chia hết cho 2
Câu 5 (2 điểm): Có 2 hộp . Hộp I có: 5 bi màu đỏ, 7 bi màu xanh. Hộp II có: 4 bi màu đỏ, 6 bi màu xanh. Ở mỗi
hộp các bi cùng màu đôi một khác nhau.
a) Từ hộp I lấy ngẫu nhiên ra 1 bi, tiếp đó từ hộp II lấy ngẫu nhiên ra 2 bi. Tính xác suất để trong 3 bi lấy được
có đúng 1 bi đỏ và 2 bi xanh
b) Xếp ngẫu nhiên 10 bi ở hộp II thành một hàng ngang. Tính xác suất để có ít nhất hai bi đỏ xếp cạnh nhau
HƯỚNG DẪN CHẤM (ĐỀ 1-KHỐI SÁNG)
Câu
NỘI DUNG
ĐIỂM
Câu 1
a) Mỗi số có 5 chữ số đôi một khác nhau là một chỉnh hợp chập 5 của 6 phần tử của A.
Do đó số các số cần tìm là:
5
6
A
=720 số
0,5
1
b) Gọi số có 4 chữ số đôi một khác nhau có dạng:
abcd
Vì số lẽ nên d có 3 cách chọn (d thuộc tập {1,5,9})
Chọn 3 số còn lại :
3
5
A
Theo quy tắc nhân ta có số các số cần tìm: 3.
3
5
A
=180 số
0,5
0,5
0,5
Câu 2
Đặt đúng điều kiện:
3x
Biến đổi về được:
x=5 hoặc x=-5/2 (loại)
Đáp số đúng: x=5
0,5
0,5
0,5
Câu 3
Viết ra được số hạng tổng quát:
)80(22
1
83
8
2
8
8
kxCx
x
C
kkk
k
k
k
Sô hạng chứa
4
x
nếu 3k-8=4 hay k=4
Viết đúng đáp số:
11202
4
8
4
C
0,5
0,5
0,5
Câu 4
Viết được:
2
120
C
.
Gọi A là biến cố chọn được 2 số có tích chia hết cho 7
Số chia hết cho 7 có dạng: 7k ( k nguyên dương) và
17112071 kk
hay có 17
số chia hết cho 7 và 103 số không chia hết cho 7. Tích 2 số chia hết cho 7 xảy ra 1
trong 2 trường hợp sau:
TH1: cả 2 số đều chia hết cho 7: Có
2
17
C
cách chọn
TH2: 1 số chia hết 7 và một số không chia hết 7: có
1
103
1
17
.CC
cách chọn
Suy ra:
A
2
17
C
+
1
103
1
17
.CC
. Do đó:
140
37
)(
A
Ap
0,75
0,75
0,5
Câu 5
a) Gọi A là biến cố chọn được 2 cuốn sách khác môn
11
,BA
lần lượt là biến cố chọn được sách Toán, Lý từ Giá I
22
,BA
lần lượt là biến cố chọn được sách Toán, Lý từ Giá II
Khi đó
1
A
và
2
B
độc lập;
2
A
và
1
B
độc lập;
21
BA
và
12
BA
xung khắc;
1221
BABAA
Suy ra
33
16
11
6
.
12
4
12
8
.
11
5
)().()().()(
1221
BpApBpApAp
0,25
0,25
0,5
b) Viết được
8
20
C
Gọi A là biến cố chọn được không quá 6 nữ. Suy ra
A
là biến cố: 7 nữ và 1
nam .hoặc 8 nữ
0,25
0,25
Suy ra
442
11
.
)(.
8
20
1
9
7
11
8
11
1
9
7
11
8
11
C
CCC
ApCCC
A
Vậy:
442
431
442
11
11 ApAp
0,5
ĐỀ 2 (KHỐI SÁNG)
Câu
NỘI DUNG
ĐIỂM
Câu 1
a)
6
7
A
= 5040 (Thang điểm như đề 1)
1,5
b) 2.
240
3
6
A
(Thang điểm như đề 1)
1,5
Câu 2
Đặt đúng điều kiện:
3x
Biến đổi về được:
0152
2
xx
x=5 hoặc x=-3 (loại)
Đáp số đúng: x=5
0,5
0,5
0,5
Câu 3
Viết ra được số hạng tổng quát:
)90(22
1
93
9
2
9
9
kxCx
x
C
kk
k
k
k
k
Sô hạng không chứa
x
nếu 3k-9=0 hay k=3
Viết đúng đáp số:
6722
3
9
3
C
0,5
0,5
0,5
Câu 4
Viết được:
2
100
C
. Gọi A là biến cố chọn được 2 số có tích chia hết cho 7
Lý luận như đề 1: có 14 số chia hết cho 7; 86 số không chia hết cho 7
TH1: cả 2 số đều chia hết cho 7: Có
2
14
C
cách chọn
TH2: 1 số chia hết 7 và một số không chia hết 7: có
1
86
1
14
.CC
cách chọn
Suy ra:
A
2
14
C
+
1
86
1
14
.CC
. Do đó:
990
259
)(
A
Ap
0,75
0,75
0,5
Câu 5
a) Gọi A là biến cố chọn được 2 cuốn sách cùng môn (các biến cố gọi như đề 1)
Khi đó
1
A
và
2
A
độc lập;
1
B
và
2
B
độc lập;
21
AA
và
21
BB
xung khắc;
2121
BBAAA
Suy ra
55
28
11
6
.
10
6
11
5
.
10
4
)().()().()(
2121
BpBpApApAp
0,25
0,25
0,5
b) Viết được
7
18
C
Gọi A là biến cố chọn được không quá 5 nữ. Suy ra
A
là biến cố: 6 nữ và 1 nam
.hoặc 7 nữ
Suy ra
442
25
.
)(.
7
18
1
8
6
10
7
10
1
8
6
10
7
10
C
CCC
ApCCC
A
Vậy:
442
417
442
25
11 ApAp
0,25
0,25
0,5
Ghi chú: Nếu HS làm cách khác mà đúng thì vẫn cho điểm tối đa.
HƯỚNG DẪN CHẤM (ĐỀ 1-KHỐI CHIỀU)
Câu
NỘI DUNG
ĐIỂM
Câu 1
a)Mỗi số có 4 chữ số đôi một khác nhau là một chỉnh hợp chập 4 của 5 phần tử của E.
Do đó số các số cần tìm là:
4
5
A
=120 số
0,5
1
a) Gọi số có 3 chữ số đôi một khác nhau có dạng:
abc
Vì chia hết cho 5 nên c=5 hay c có 1 cách chọn
Chọn 2 số còn lại có:
2
4
A
cách chọn
Theo quy tắc nhân ta có số các số cần tìm: 1.
2
4
A
=12 số
0,5
0,5
0,5
Câu 2
Đặt đúng điều kiện:
3x
Biến đổi về được:
0123x
x=4 (thỏa điều kiện)
Đáp số đúng: x=4
0,5
0,5
0,5
Câu 3
Viết ra được số hạng tổng quát:
)80(2
2
316
8
8
2
8
kxC
x
xC
kk
k
k
k
k
Sô hạng chứa
7
x
nếu 16-3k=7 hay k=3
Viết đúng đáp số:
773
8
3
4482 xxC
0,5
0,5
0,5
Câu 4
Viết được:
5
19
C
.
Gọi A là biến cố chọn được 5 số có tổng chia hết cho 2
Số chia hết cho 2 có dạng: 2k ( k nguyên dương) và
911921 kk
hay có 9 số
chẵn và 10 số lẽ. Tổng 5 số chia hết cho 2 xảy ra 1 trong 3 trường hợp sau:
TH1: cả 5 số đều là số chẵn: Có
5
9
C
cách chọn
TH2: 3 số chẵn và 2 số lẽ: có
2
10
3
9
.CC
cách chọn
TH3: 1 số chẵn và 4 số lẽ: có
4
10
1
9
.CC
Suy ra:
A
5
9
C
+
2
10
3
9
.CC
+
4
10
1
9
.CC
. Do đó:
323
161
)(
A
Ap
0,75
0,75
0,5
Câu 5
a) Gọi A là biến cố lấy được đúng 2 bi đỏ và 1 bi xanh
11
,BA
lần lượt là biến cố lấy được 2 bi đỏ; 1 bi đỏ và 1 bi xanh từ Hộp I
22
,BA
lần lượt là biến cố lấy được 1 bi đỏ; 1 bi xanh từ Hộp II
Khi đó
1
A
và
2
B
độc lập;
2
A
và
1
B
độc lập;
21
BA
và
12
BA
xung khắc;
1221
BABAA
Suy ra
33
10
.
..)().()().()(
2
12
1
7
1
5
1
10
1
4
1
10
1
6
2
12
2
5
1221
C
CC
C
C
C
C
C
C
BpApBpApAp
0,25
0,25
0,5
b) Viết được:
!12
Gọi A là biến cố có ít nhất hai bi đỏ xếp cạnh nhau. Suy ra
A
là biến cố không có
hai bi đỏ nào xếp cạnh nhau .
0,25
Xếp 7 bi xanh trước, có: 7! cách sắp xếp
Mỗi lần sắp xếp 7 bi xanh cho ta 7 vách ngăn (mỗi bi xem như một vách ngăn) tạo
thành 8 vị trí trống (gồm 6 vị trí trống giữa 7 bi và 2 đầu hàng). Muốn không có 2 bi
đỏ nào đứng cạnh nhau thì 5 bi đỏ này phải xếp vào 5 vị trí trống trong 8 vị trí trống
(mỗi vị trí một bi). Số cách xếp là:
5
8
A
. Theo quy tắc nhân:
99
7
!12
!.7
!.7
5
8
5
8
A
ApA
A
A
. Vậy:
99
92
99
7
11 ApAp
0,25
0,5
ĐỀ 2 (CHIỀU)
Câu
NỘI DUNG
ĐIỂM
Câu 1
c)
3
6
A
= 120 (Thang điểm như đề 1)
1,5
d) 5.
300
3
5
A
(Thang điểm như đề 1)
1,5
Câu 2
Đặt đúng điều kiện:
3x
Biến đổi về được:
0324
2
xx
x=4 hoặc x=-8 (loại)
Đáp số đúng: x=4
0,5
0,5
0,5
Câu 3
Viết ra được số hạng tổng quát:
)100(2
2
320
10
10
2
10
kxC
x
xC
kk
k
k
k
k
Sô hạng chứa
8
x
nếu 20-3k=8 hay k=4
Viết đúng đáp số:
884
10
4
33602 xxC
0,5
0,5
0,5
Câu 4
Viết được:
5
25
C
.
Gọi A là biến cố chọn được 5 số có tổng không chia hết cho 2
Lý luận tương tự đề 1: Có 12 chẵn và 13 lẽ. (Lý luận tương tự đề 1: có 3 trường hợp)
Suy ra:
A
5
13
C
+
2
12
3
13
.CC
+
4
12
1
13
.CC
. Do đó:
805
403
)(
A
Ap
0,75
0,75
0,5
Câu 5
a) Gọi A là biến cố lấy được đúng 2 bi đỏ và 1 bi xanh
11
,BA
lần lượt là biến cố lấy được 1 bi đỏ, 1 bi xanh từ Hộp I
22
,BA
lần lượt là biến cố lấy được 1 bi đỏ và 1 xanh, 2 bi xanh từ Hộp II
Khi đó
1
A
và
2
B
độc lập;
2
A
và
1
B
độc lập;
21
BA
và
12
BA
xung khắc;
1221
BABAA
Suy ra
20
9
.
..)().()().()(
2
10
1
4
1
6
1
12
1
7
2
10
2
6
1
12
1
5
1221
C
CC
C
C
C
C
C
C
BpApBpApAp
0,25
0,25
0,5
b) Lý luận như đề 1:
6
5
1
6
1
!10
!.6
4
7
ApAp
A
Ap
A
.(thang điểm
như đề 1)
1,0
Ghi chú: Nếu HS làm cách khác mà đúng thì vẫn cho điểm tối đa.
MA TRẬN ĐỀ KIỂM TRA MỘT TIẾT GIỮA CHƯƠNG II
MÔN ĐS-GT 11 NC
Mạch kiến thức
Mức độ nhận thức
Cộng
1
2
3
4
Các quy tắc
đếm
HV-CH-TH
1
1,5
1
1,5
1
1,5
3
4,5
Nhị thức Niu-
Tơn
1
1,5
1
1,5
Biến cố và xác
suất (ĐN cổ
điển)
1
0,75
1
1,25
2
2
Các quy tắc
tính xác suất
1
1
1
1
2
2
Tổng
1
1,5
3
3,75
3
3,75
1
1
8
10
MÔ TẢ TIÊU CHÍ NỘI DUNG KIỂM TRA
Câu 1 (3 điểm): Bài toán lập số (có 2 câu a, b)
Câu 2 (1,5 điểm): Giải phương trình chứa
n
k
n
k
n
PAC ;;
Câu 3 ( 1,5 điểm): Tìm hệ số hay số hạng trong khai triển Niu-Tơn của một biểu thức
Câu 4 (2 điểm): Tính xác suất của một biến cố
Câu 5 (2 điểm): Tính xác suất ( vận dụng quy tắc tính xác suất)
| 1/7
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


TRƯỜNG THPT TX QUẢNG TRỊ KIỂM TRA MỘT TIẾT TOÁN 11 NC
Tổ Toán Môn: ĐS-GT. ĐỀ SỐ :1 (Khối sáng)
Câu 1 (3 điểm): Cho A    9 , 8 , 6 , 5 , 2 , 1
a) Từ A lập được bao nhiêu số có 5 chữ số đôi một khác nhau
b) Từ A lập được bao nhiêu số lẽ có 4 chữ số đôi một khác nhau
Câu 2 (1,5 điểm): Giải phương trình: A3  Cx2 14x (với x là số nguyên dương) x x 8   Câu 3 1
(1,5 điểm): Tìm hệ số của 4
x trong khai triển biểu thức 2
  2x  (với x  0 ).  x
Câu 4 (2 điểm): Cho C    120 , 119 ,..., 3 , 2 , 1
. Chọn ngẫu nhiên 2 số từ C. Tính xác suất để chọn được 2 số có tích chia hết cho 7
Câu 5 (2 điểm):
a) Có 2 giá sách. Giá I có: 5 sách Toán, 6 sách Lý. Giá II có: 4 sách Toán, 8 sách Lý. Ở mỗi giá các cuốn
sách cùng môn đôi một khác nhau. Từ mỗi giá chọn ngẫu nhiên 1 cuốn sách. Tính xác suất để chọn được 2 cuốn sách khác môn.
b) Một nhóm có 20 học sinh trong đó có 9 nam và 11 nữ. Chọn ngẫu nhiên 8 học sinh. Tính xác suất để trong 8
học sinh chọn được luôn có không quá 6 nữ.
TRƯỜNG THPT TX QUẢNG TRỊ KIỂM TRA MỘT TIẾT TOÁN 11 NC
Tổ Toán Môn: ĐS-GT. ĐỀ SỐ : 2 (Khối sáng)
Câu 1 (3 điểm): Cho B    9 , 7 , 6 , 5 , 3 , 2 , 1
a) Từ B lập được bao nhiêu số có 6 chữ số đôi một khác nhau
b) Từ B lập được bao nhiêu số chẵn có 4 chữ số đôi một khác nhau
Câu 2 (1,5 điểm): Giải phương trình: A3  C
2 2  16x (với x là số nguyên dương) x x 9   Câu 3 1
(1,5 điểm): Tìm số hạng không chứa x trong khai triển biểu thức 2
  2x  (với x  0 ).  x
Câu 4 (2 điểm): Cho D   1 , 99 ,..., 3 , 2 , 1 0 
0 . Chọn ngẫu nhiên 2 số từ D. Tính xác suất để chọn được 2 số có tích chia hết cho 7
Câu 5 (2 điểm):
a) Có 2 giá sách: Giá I có: 4 sách Toán, 6 sách Lý. Giá II có: 5 sách Toán, 6 sách Lý. Ở mỗi giá các cuốn sách
cùng môn đôi một khác nhau. Từ mỗi giá chọn ngẫu nhiên 1 cuốn sách. Tính xác suất để chọn được 2 cuốn sách cùng môn.
b) Một nhóm có 18 học sinh trong đó có 8 nam và 10 nữ. Chọn ngẫu nhiên 7 học sinh. Tính xác suất để trong 7 học
sinh chọn được luôn có không quá 5 nữ.
TRƯỜNG THPT TX QUẢNG TRỊ KIỂM TRA MỘT TIẾT TOÁN 11 NC
Tổ Toán Môn: ĐS-GT. ĐỀ SỐ : 1 (Khối chiều)
Câu 1 (3 điểm): Cho E    8 , 7 , 6 , 5 , 1
a) Từ E lập được bao nhiêu số có 4 chữ số đôi một khác nhau
b) Từ E lập được bao nhiêu số có 3 chữ số đôi một khác nhau và chia hết cho 5 Câu 2 1 2 2 6
(1,5 điểm): Giải phương trình: x 3 A A   C
10 (với x là số nguyên dương) 2 2x x x x 8   Câu 3 2
(1,5 điểm): Tìm số hạng chứa 7
x trong khai triển biểu thức 2
x   (với x  0 ).  x
Câu 4 (2 điểm): Cho S   ,.. 3 , 2 , 1 .,  19 , 18
. Chọn ngẫu nhiên 5 số từ S. Tính xác suất để chọn được 5 số có tổng chia hết cho 2
Câu 5 (2 điểm): Có 2 hộp . Hộp I có: 5 bi màu đỏ, 7 bi màu xanh. Hộp II có: 4 bi màu đỏ, 6 bi màu xanh. Ở mỗi
hộp các bi cùng màu đôi một khác nhau.
a) Từ hộp I lấy ngẫu nhiên ra 2 bi, tiếp đó từ hộp II lấy ngẫu nhiên ra 1 bi. Tính xác suất để trong 3 bi lấy được
có đúng 2 bi đỏ và 1 bi xanh
b) Xếp ngẫu nhiên 12 bi ở hộp I thành một hàng ngang. Tính xác suất để có ít nhất hai bi đỏ xếp cạnh nhau
TRƯỜNG THPT TX QUẢNG TRỊ KIỂM TRA MỘT TIẾT TOÁN 11 NC
Tổ Toán Môn: ĐS-GT. ĐỀ SỐ : 2 (Khối chiều)
Câu 1 (3 điểm): Cho F    9 , 6 , 5 , 4 , 2 , 1
a) Từ F lập được bao nhiêu số có 3 chữ số đôi một khác nhau
b) Từ F lập được bao nhiêu số có 4 chữ số đôi một khác nhau và không chia hết cho 5 Câu 2 12 x 3  2 1
(1,5 điểm): Giải phương trình: 2 C
A A  28 (với x là số nguyên dương) x x x 2 2x 10   Câu 3 2
(1,5 điểm): Tìm số hạng chứa 8
x trong khai triển biểu thức 2
x   (với x  0 ).  x
Câu 4 (2 điểm): Cho T   , 1 ,. 3 , 2 .., , 24 
25 . Chọn ngẫu nhiên 5 số từ T. Tính xác suất để chọn được 5 số có tổng
không chia hết cho 2
Câu 5 (2 điểm): Có 2 hộp . Hộp I có: 5 bi màu đỏ, 7 bi màu xanh. Hộp II có: 4 bi màu đỏ, 6 bi màu xanh. Ở mỗi
hộp các bi cùng màu đôi một khác nhau.
a) Từ hộp I lấy ngẫu nhiên ra 1 bi, tiếp đó từ hộp II lấy ngẫu nhiên ra 2 bi. Tính xác suất để trong 3 bi lấy được
có đúng 1 bi đỏ và 2 bi xanh
b) Xếp ngẫu nhiên 10 bi ở hộp II thành một hàng ngang. Tính xác suất để có ít nhất hai bi đỏ xếp cạnh nhau
HƯỚNG DẪN CHẤM (ĐỀ 1-KHỐI SÁNG) Câu NỘI DUNG ĐIỂM
a) Mỗi số có 5 chữ số đôi một khác nhau là một chỉnh hợp chập 5 của 6 phần tử của A. 0,5 Câu 1
Do đó số các số cần tìm là: 5 A =720 số 1 6
b) Gọi số có 4 chữ số đôi một khác nhau có dạng: abcd
Vì số lẽ nên d có 3 cách chọn (d thuộc tập {1,5,9}) 0,5 Chọn 3 số còn lại : 3 0,5 A 5 0,5
Theo quy tắc nhân ta có số các số cần tìm: 3. 3 A =180 số 5
Câu 2 Đặt đúng điều kiện: x  3 0,5
Biến đổi về được: 2 2
x  5x  25  0  x=5 hoặc x=-5/2 (loại) 0,5 Đáp số đúng: x=5 0,5 Câu 3 8  k 0,5 k 1  k
Viết ra được số hạng tổng quát: C   xk k kC xk  8 2 2 2 3 8 (0 ) 8 8  x Sô hạng chứa 4 0,5
x nếu 3k-8=4 hay k=4 0,5 Viết đúng đáp số: 24 4 C  1120 8
Câu 4 Viết được: 2   C . 0,75 120
Gọi A là biến cố chọn được 2 số có tích chia hết cho 7
Số chia hết cho 7 có dạng: 7k ( k nguyên dương) và 1  7k 120 1  k 17 hay có 17
số chia hết cho 7 và 103 số không chia hết cho 7. Tích 2 số chia hết cho 7 xảy ra 1 trong 2 trường hợp sau: 0,75
TH1: cả 2 số đều chia hết cho 7: Có 2 C cách chọn 17
TH2: 1 số chia hết 7 và một số không chia hết 7: có 1 1 C .C cách chọn 17 103  37 Suy ra:   2 C + 1 1 C .C . Do đó: p( )  A AA 17 17 103  140 0,5 Câu 5
a) Gọi A là biến cố chọn được 2 cuốn sách khác môn 0,25
A , B lần lượt là biến cố chọn được sách Toán, Lý từ Giá I 1 1
A , B lần lượt là biến cố chọn được sách Toán, Lý từ Giá II 2 2 Khi đó
A và B độc lập; A và B độc lập; A B và A B xung khắc; 1 2 2 1 1 2 2 1
A A B A B 0,25 1 2 2 1 5 8 4 6 16 Suy ra p( )
A p(A ).p(B )  p(A ).p(B )  .  .  1 2 2 1 11 12 12 11 33 0,5 b) Viết được 8   C 0,25 20
Gọi A là biến cố chọn được không quá 6 nữ. Suy ra A là biến cố: 7 nữ và 1 nam .hoặc 8 nữ 0,25 8 7 C C C 8 7 1 . 1 11 Suy ra 
C C .C p( ) 11 11 9 A   11 11 9 A 8 C 442 0,5 20 11 431 Vậy: p 
A  1 p  A  1  442 442 ĐỀ 2 (KHỐI SÁNG) Câu NỘI DUNG ĐIỂM a) 6
A = 5040 (Thang điểm như đề 1) 1,5 7 Câu 1 b) 2. 3
A  240 (Thang điểm như đề 1) 1,5 6
Câu 2 Đặt đúng điều kiện: x  3 0,5 Biến đổi về được: 2
x  2x 15  0  x=5 hoặc x=-3 (loại) 0,5 Đáp số đúng: x=5 0,5 Câu 3 9  k 0,5 k 1  k
Viết ra được số hạng tổng quát: C    x   k k kC xk  9  2 2  2 3 9 (0 ) 9 9  x Sô hạng không chứa 0,5
x nếu 3k-9=0 hay k=3 0,5
Viết đúng đáp số:  23 3 C  672  9
Câu 4 Viết được: 2
  C . Gọi A là biến cố chọn được 2 số có tích chia hết cho 7 0,75 100 Lý luận như đề
1: có 14 số chia hết cho 7; 86 số không chia hết cho 7
TH1: cả 2 số đều chia hết cho 7: Có 2 C cách chọn 14
TH2: 1 số chia hết 7 và một số không chia hết 7: có 1 1
C .C cách chọn 14 86 0,75  259 Suy ra:   2 C + 1 1
C .C . Do đó: p( )  A AA 14 14 86  990 0,5 Câu 5
a) Gọi A là biến cố chọn được 2 cuốn sách cùng môn (các biến cố gọi như đề 1) 0,25
Khi đó A và A độc lập; B và B độc lập; A A và B B xung khắc; 1 2 1 2 1 2 1 2
A A A B B 1 2 1 2 0,25 4 5 6 6 28 Suy ra p( )
A p(A ).p(A )  p(B ).p(B )  .  .  1 2 1 2 10 11 10 11 55 0,5 b) Viết được 7   C 0,25 18
Gọi A là biến cố chọn được không quá 5 nữ. Suy ra A là biến cố: 6 nữ và 1 nam .hoặc 7 nữ 7 6 0,25 C C C 7 6 1 . 1 25 Suy ra 
C C .C p( ) 10 10 8 A   10 10 8 A 7 C 442 18 25 417 Vậy: p 
A  1 p  A  1  442 442 0,5
Ghi chú: Nếu HS làm cách khác mà đúng thì vẫn cho điểm tối đa.
HƯỚNG DẪN CHẤM (ĐỀ 1-KHỐI CHIỀU) Câu NỘI DUNG ĐIỂM
a)Mỗi số có 4 chữ số đôi một khác nhau là một chỉnh hợp chập 4 của 5 phần tử của E. 0,5 Câu 1
Do đó số các số cần tìm là: 4 A =120 số 1 5
a) Gọi số có 3 chữ số đôi một khác nhau có dạng: abc
Vì chia hết cho 5 nên c=5 hay c có 1 cách chọn 0,5 Chọn 2 số còn lại có: 2 0,5 A cách chọn 4 0,5
Theo quy tắc nhân ta có số các số cần tìm: 1. 2 A =12 số 4
Câu 2 Đặt đúng điều kiện: x  3 0,5
Biến đổi về được: 3x 12  0  x=4 (thỏa điều kiện) 0,5 Đáp số đúng: x=4 0,5 Câu 3 k 0,5 8k k   2 2
Viết ra được số hạng tổng quát: C x     k kC x kk  8    2 16 3 (0 ) 8 8  x Sô hạng chứa 7 0,5
x nếu 16-3k=7 hay k=3 0,5
Viết đúng đáp số:  23 3 7 7 C x  448  x 8
Câu 4 Viết được: 5   C . 0,75 19
Gọi A là biến cố chọn được 5 số có tổng chia hết cho 2
Số chia hết cho 2 có dạng: 2k ( k nguyên dương) và 1 2k 19 1 k  9 hay có 9 số
chẵn và 10 số lẽ. Tổng 5 số chia hết cho 2 xảy ra 1 trong 3 trường hợp sau:
TH1: cả 5 số đều là số chẵn: Có 5 C cách chọn 0,75 9
TH2: 3 số chẵn và 2 số lẽ: có 3 2
C .C cách chọn 9 10
TH3: 1 số chẵn và 4 số lẽ: có 1 4 C .C 9 10  161 0,5 Suy ra:   5 C + 3 2 C .C + 1 4
C .C . Do đó: p( )  A AA 9 9 10 9 10  323 Câu 5
a) Gọi A là biến cố lấy được đúng 2 bi đỏ và 1 bi xanh 0,25
A , B lần lượt là biến cố lấy được 2 bi đỏ; 1 bi đỏ và 1 bi xanh từ Hộp I 1 1
A , B lần lượt là biến cố lấy được 1 bi đỏ; 1 bi xanh từ Hộp II 2 2 Khi đó
A và B độc lập; A và B độc lập; A B và A B xung khắc; 1 2 2 1 1 2 2 1
A A B A B 0,25 1 2 2 1 2 1 1 1 C C C C . 1 C 10 Suy ra p( )
A p( A ). p(B )  p( A ). p(B ) 5  . 6 4  . 5 7  1 2 2 1 2 1 1 2 0,5 C C C C 33 12 10 10 12 b) Viết được:   ! 12 0,25
Gọi A là biến cố có ít nhất hai bi đỏ xếp cạnh nhau. Suy ra A là biến cố không có
hai bi đỏ nào xếp cạnh nhau .
Xếp 7 bi xanh trước, có: 7! cách sắp xếp
Mỗi lần sắp xếp 7 bi xanh cho ta 7 vách ngăn (mỗi bi xem như một vách ngăn) tạo 0,25
thành 8 vị trí trống (gồm 6 vị trí trống giữa 7 bi và 2 đầu hàng). Muốn không có 2 bi
đỏ nào đứng cạnh nhau thì 5 bi đỏ này phải xếp vào 5 vị trí trống trong 8 vị trí trống
(mỗi vị trí một bi). Số cách xếp là: 5
A . Theo quy tắc nhân: 8 5    A A 7 92 !. 7 5 A p A    . Vậy: p 
A  1 p  A  1  8   !. 7 7 8 A  ! 12 99 99 99 0,5 ĐỀ 2 (CHIỀU) Câu NỘI DUNG ĐIỂM c) 3
A = 120 (Thang điểm như đề 1) 1,5 6 Câu 1 d) 5. 3
A  300 (Thang điểm như đề 1) 1,5 5
Câu 2 Đặt đúng điều kiện: x  3 0,5 Biến đổi về được: 2
x  4x  32  0  x=4 hoặc x=-8 (loại) 0,5 Đáp số đúng: x=4 0,5 Câu 3 k 0,5 10k k   2 2
Viết ra được số hạng tổng quát: C x    k kC x kk  10   2 20 3 (0 10) 10  x Sô hạng chứa 8 0,5
x nếu 20-3k=8 hay k=4 0,5
Viết đúng đáp số: 24 4 8 8 C x  3360 x 10
Câu 4 Viết được: 5   C . 0,75 25
Gọi A là biến cố chọn được 5 số có tổng không chia hết cho 2 Lý luận tương tự 0,75
đề 1: Có 12 chẵn và 13 lẽ. (Lý luận tương tự đề 1: có 3 trường hợp)  403 Suy ra:   5 C + 3 2 C .C + 1 4
C .C . Do đó: p( )  A AA 13 13 12 13 12  0,5 805 Câu 5
a) Gọi A là biến cố lấy được đúng 2 bi đỏ và 1 bi xanh 0,25
A , B lần lượt là biến cố lấy được 1 bi đỏ, 1 bi xanh từ Hộp I 1 1
A , B lần lượt là biến cố lấy được 1 bi đỏ và 1 xanh, 2 bi xanh từ Hộp II 2 2 Khi đó
A và B độc lập; A và B độc lập; A B và A B xung khắc; 1 2 2 1 1 2 2 1
A A B A B 0,25 1 2 2 1 1 2 1 1 C C C C . 1 C 9 Suy ra p( )
A p( A ). p(B )  p( A ). p(B ) 5  . 6 7  . 6 4  1 2 2 1 1 2 1 2 0,5 C C C C 20 12 10 12 10 p  A !. 6 4 A 1 5
b) Lý luận như đề 1: 7 A     p 
A  1 p  A   .(thang điểm ! 10 6 6 1,0 như đề 1)
Ghi chú: Nếu HS làm cách khác mà đúng thì vẫn cho điểm tối đa.
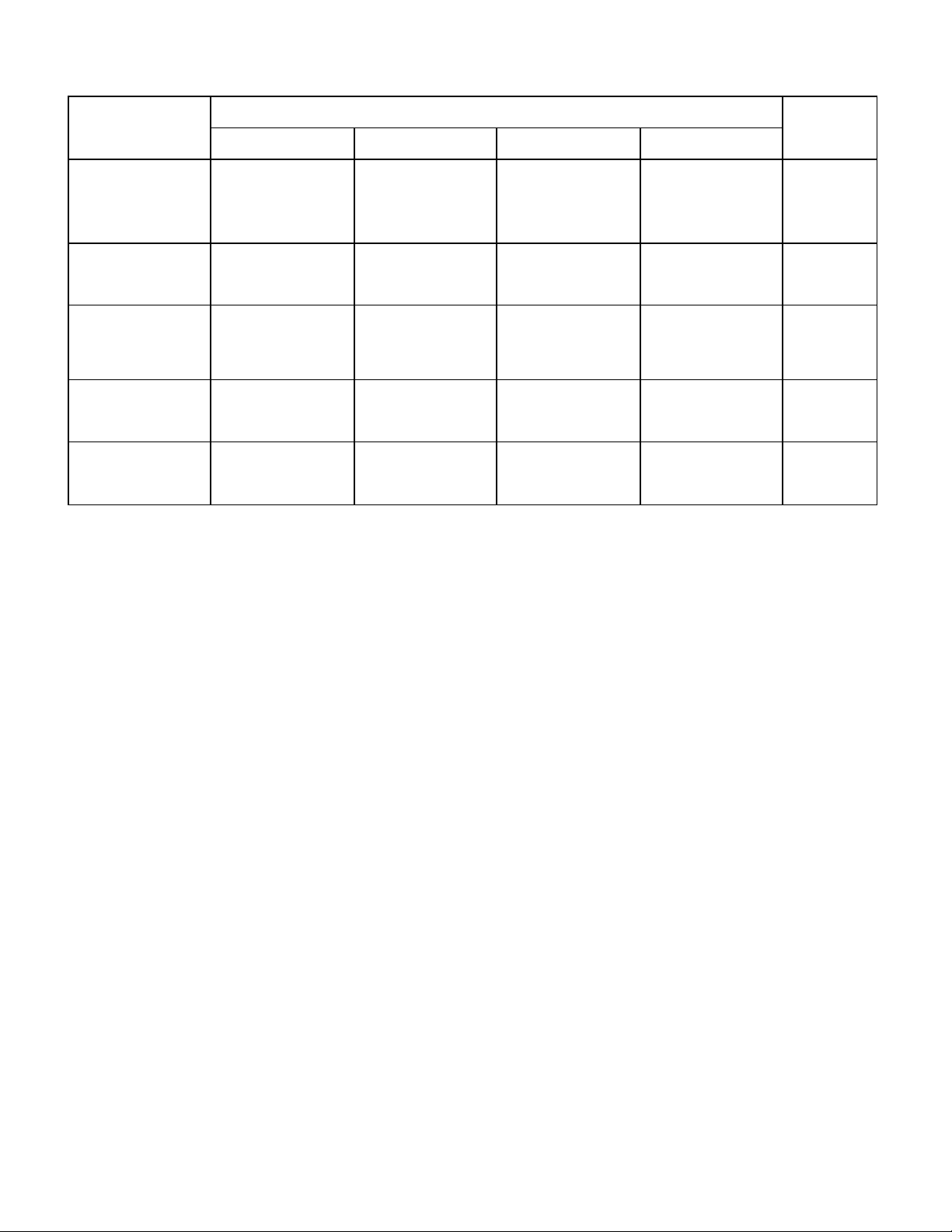
MA TRẬN ĐỀ KIỂM TRA MỘT TIẾT GIỮA CHƯƠNG II MÔN ĐS-GT 11 NC Mạch kiến thức
Mức độ nhận thức Cộng 1 2 3 4 Các quy tắc 1 1 1 3 đếm 1,5 1,5 1,5 4,5 HV-CH-TH Nhị thức Niu- 1 1 Tơn 1,5 1,5 Biến cố và xác 1 1 2 suất (ĐN cổ 0,75 1,25 2 điển) Các quy tắc 1 1 2 tính xác suất 1 1 2 1 3 3 1 8 Tổng 1,5 3,75 3,75 1 10
MÔ TẢ TIÊU CHÍ NỘI DUNG KIỂM TRA
Câu 1 (3 điểm): Bài toán lập số (có 2 câu a, b)
Câu 2 (1,5 điểm): Giải phương trình chứa k k
C ; A ; P n n n
Câu 3 ( 1,5 điểm): Tìm hệ số hay số hạng trong khai triển Niu-Tơn của một biểu thức
Câu 4 (2 điểm): Tính xác suất của một biến cố
Câu 5 (2 điểm): Tính xác suất ( vận dụng quy tắc tính xác suất)