
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯNG YÊN
ĐỀ KIỂM TRA ĐỊNH KÌ
TRƯỜNG THPT TRIỆU QUANG PHỤC
MÔN GIẢI TÍCH LỚP 11- CHƯƠNG 4
Thời gian làm bài:45 phút
(25 câu trắc nghiệm) Mã đề 730
Họ và tên học sinh : Lớp:
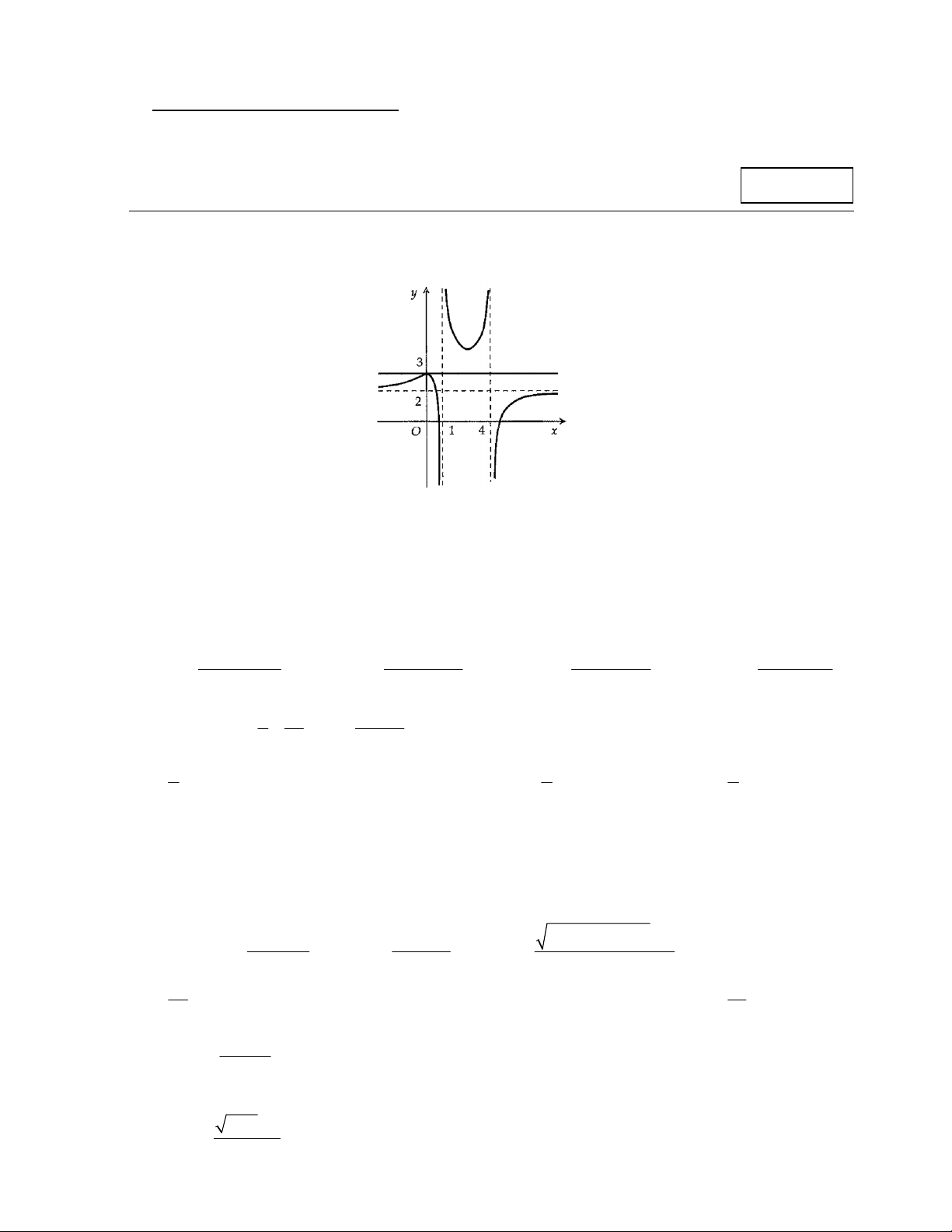
Câu 1. Cho hàm số y f (x) có đồ thị như hình dưới đây, chọn khẳng định đúng:
A. Hàm số liên tục trên ;4 .
B. Hàm số liên tục trên 1; .
C. Hàm số liên tục trên .
D. Hàm số liên tục trên 1;4 . Câu 2. 3
lim 2n 3n bằng A. 3 . B. . C. 2 . D. .
Câu 3. Trong bốn giới hạn sau , giới hạn nào là ? 2 2 x x 1 3 2 1 3x x 2 4 3x x 1 2 3x x 5 A. lim . B. lim . C. lim . D. lim . x 3 x 2
x 5 x 2x 2
x 2 x x x 1 2x 1 5
3n 2n
Câu 4. Tổng S ...
... có giá trị bằng 6 36 6n 2 3 1 A. . B. 1. C. . D. . 3 4 2
Câu 5. Khẳng định đúng là
A. lim f x a lim f x a .
B. lim f x a lim f x lim f x . x 0 x x x x 0 x 0 x 0 x x 0 x
C. lim f x a lim f x a .
D. lim f x a lim f x lim f x a . x 0 x x x x 0 x 0 x 0 x x 0 x f x 5 g x 1
f x.g x 4 3 Câu 6. Nếu lim 2 và lim 3 thì lim bằng x 1 x 1 x 1 x 1 x 1 x 1 23 17 A. . B. 7 . C. 17 . D. 7 6 3 2x x Câu 7. lim bằng 2
x x 2 A. . B. 2. C. 1. D. . 1 x 1 Câu 8. lim bằng x0 x 1/3 - Mã đề 730 1 1 A. . B. . C. 0 . D. . 2 2 4x 1 1 khi x 0
Câu 9. Tìm a để hàm số 2
f (x) ax (2a 1)
liên tục tại x 0 . 3 khi x 0 1 1 1 A. . B. C. . D. 1. 6 2 4 3n 5 Câu 10. Tính lim . Kết quả bằng 4n 2 3 2 A. . B. 3 . C. . D. 0 . 4 3 2
3x 2 4 x a a Câu 11. Biết lim
(với là phân số tối giản).Tính P a b . 2 x 1 x 1 b b A. P 5 . B. P 1 . C. P 2 .
D. P 3 . 3 2n 5n 3 Câu 12. lim bằng 3 2 3n n 2 3 A. +. B. . C. 3. D. . 3 2 3
ax 1 bx 1 1 khi x 0
Câu 13. Biết hàm số f x x
,( a , b là các số thực dương khác 0)
a b 2 khi x 0
liên tục tại điểm x 0 . Tìm giá trị lớn nhất của biểu thức P . a b . 5 3 36 A. . B. 3. C. . D. . 9 4 49
Câu 14. Cho lim f x L 0 . Trong các mệnh đề sau,mệnh đề nào sai? x 0 x 1 1 A. f x 2 2 lim L . B. f x 3 3 lim L . C. lim .
D. lim f x L . x x 0 x f x 0 x x 0 x L x 0 x
Câu 15. Hàm số gián đoạn tại điểm x 1 là hàm số 0 x 1 2 x 1 x 2 A. y . B. 2
y (x 1)(x 11) . C. y . D. y . 2 x 1 x 1 x 11 2 3
x 7x 11 Câu 16. lim bằng 2 x x x 3 A. 0 . B. . C. 3 . D. 3 .
Câu 17. Mệnh đề nào sau đây là mệnh đề đúng?
A. Nếu limu và limv thì lim(u v ) 0 . n n n n
B. Nếu (u ) là dãy số tăng thì limu . n n C. Nếu n
u a và 1 a 1 thì limu 0 . n n
D. Một dãy số có giới hạn thì luôn luôn tăng hoặc luôn luôn giảm. 2
x 4x 3 khi x 3
Câu 18. Giá trị của a để hàm số f x x 3
liên tục tại x 3 là khi x 3 a 2/3 - Mã đề 730 A. 2 . B. 4 . C. 1 . D. 2 . 1
Câu 19. Cho phương trình 2 2 2 2
(m 1)x (3m 2)x 2m 0 . Khẳng định nào sau đây đúng ? 2
A. Phương trình f (x) 0 có hai nghiệm dương phân biệt với mọi m .
B. Phương trình f (x) 0 có đúng 1 nghiệm với mọi m .
C. Phương trình f (x) 0 có hai nghiệm âm phân biệt với mọi m .
D. Phương trình f (x) 0 vô nghiệm với mọi m .
Câu 20. Kết quả đúng của 3
lim x x 1 bằng x A. 0 . B. 1. C. . D. . n 2 Câu 21. Tính lim . Kết quả là 2 n 3n 1 2 A. 0 . B. 1 . C. . D. 2 . 3 2 2n 3n Câu 22. lim bằng 3n 1 5 3 A. 0 . B. C. . D. . 7 4 2 x 3x 2 Câu 23. lim bằng 3 x 1 x 1 1 1 2 A. . B. . C. 0 . D. . 3 3 3 2 2x x 2 Câu 24. lim bằng 2 1 x ( ) 3x 2x 1 3 A. 1. B. . C. 2. D. . Câu 25. 4 2 lim ( 2
x 3x 4) bằng x A. – 2. B. . C. 2. D. .
---------------------- HẾT --------------------- 3/3 - Mã đề 730




