Đề kiểm tra ĐS và GT 11 chương 1 năm 2019 – 2020 trường chuyên Hùng Vương – Gia Lai

Giới thiệu đến quý thầy, cô giáo và các em học sinh khối 11 đề kiểm tra Đại số và Giải tích 11 chương 1 năm học 2019 – 2020 trường THPT chuyên Hùng Vương – Gia Lai

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

2 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Trang 1/2
TRƯỜNG THPT CHUYÊN
HÙNG VƯƠNG
TỔ TOÁN
ĐỀ KIỂM TRA MỘT TIẾT - HỌC KÌ I (2019 – 2020)
MÔN: TOÁN – LỚP 11 (SỐ 1)
Thời gian: 45 phút (20 câu TN - 4 câu TL)
Mã đề 114
Họ tên học sinh: ..................................................................... Số báo danh: .........................
I. TRẮC NGHIỆM (8 điểm)
Câu 1: Trong các hàm số sau, hàm số nào là hàm số tuần hoàn?
A.
sin cos
y x x x
B.
3 2siny x x
C.
2
siny x x
D.
sin 2 cosy x x
Câu 2: Phương trình
3 sin cos 1x x
tương đương với phương trình nào sau đây?
A.
sin 1
6
x
B.
1
sin
6 2
x
C.
1
sin
6 2
x
D.
cos
x
Câu 3: Phương trình
2 2
sin 4sin .cos 3cos 0
x x x x
có tập nghiệm trùng với tập nghiệm của phương
trình nào sau đây?
A.
cos 0
x
B.
cot 1x
C.
tan 1 3cot 1 0
x x
D.
tan 3
x
Câu 4: Trong các phương trình sau, phương trình nào vô nghiệm?
A.
2019
cos
2020
x
B.
cot 2020
x
C.
sin x
D.
tan 2019
x
Câu 5: Phương trình
2
3 tan 1 sin 1 0
x x
có nghiệm là
A.
6
x k
B.
6
x k
C.
2
6
x k
D.
2
3
x k
Câu 6: Nghiệm của phương trình
2sin 1 0
x
được biểu diễn trên đường tròn lượng giác ở hình bên dưới
là những điểm nào?
A. Điểm
,C D
B. Điểm
,D E
C. Điểm
,E F
D. Điểm
,C F
Câu 7: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
2018cos 2019siny x x
B.
sin 2019 2020cosy x x
C.
tan 2019 cot 2020y x x
D.
cot 2018 2019siny x x
Câu 8: Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số
3sin 4cos 1y x x
.
A.
2
B.
3
C.
3
D.
2
Câu 9: Tính giá trị của biểu thức
3 sin 4P x
, biết rằng
x
là nghiệm của phương trình
sin cos 2 sin cos 2
x x x x
.
A.
3
P
B.
2P
C.
1P
D.
0
P
Câu 10: Tập giá trị của hàm số
2
1 2sin cos cos 2y x x x
là
;T a b
. Tính tổng
4
a b
.
A.
0
B.
1
C.
1
D.
2
Trang 2/2
Câu 11: Hàm số nào sau đây có tính đơn điệu trên khoảng
0;
2
khác với các hàm số còn lại?
A.
2siny x
B.
4 tany x
C.
3cosy x
D.
coty x
Câu 12: Tìm điều kiện xác định của hàm số
3 2cos
sin
x
y
x
.
A.
,
2
x k k
B.
,
2
k
x k
C.
2 ,x k k
D.
,x k k
Câu 13: Nghiệm của phương trình
cos2 5sin 3 0
x x
là
A.
7
2 , 2
3 3
x k x k k
B.
7
,
6 6
x k x k k
C.
7
2 , 2
6 6
x k x k k
D.
7
,
3 3
x k x k k
Câu 14: Cho phương trình
3
sin 2 sin
4 4
x x
. Tính tổng các nghiệm thuộc khoảng
0;
của
phương trình.
A.
B.
4
C.
3
2
D.
7
2
Câu 15: Cho phương trình
3cos cos 2 cos3 1 2sin .sin 2x x x x x
. Gọi
là nghiệm lớn nhất thuộc
khoảng
0;2
của phương trình. Tính
sin
4
.
A.
1
B.
0
C.
2
2
D.
2
2
Câu 16: Phương trình
sin 1
2
x
x
có bao nhiêu nghiệm?
A.
3
nghiệm B.
2
nghiệm C. Vô số nghiệm D. Vô nghiệm
Câu 17: Có bao nhiêu giá trị nguyên dương của tham số
m
để hàm số
2
5 2 sin 1 cos2y m x m x
xác định trên
?
A.
2
B.
3
C.
4
D.
5
Câu 18: Cho phương trình
5
cos2 4cos
3 6 2
x x
. Khi đặt
cos
6
t x
, phương trình đã cho
trở thành phương trình nào sau đây?
A.
2
4 8 3 0
t t
B.
2
4 8 3 0
t t
C.
2
4 8 5 0
t t
D.
2
4 8 5 0
t t
Câu 19: Có bao nhiêu giá trị nguyên của tham số
m
để phương trình
2
cos cos
x x m m
có nghiệm?
A.
2
B.
4
C.
5
D.
3
Câu 20: Cho hàm số
sin 1
cos 2
m x
y
x
. Có bao nhiêu giá trị nguyên âm của tham số
m
thuộc đoạn
5;5
để
giá trị lớn nhất của hàm số lớn hơn 2?
A.
6
B.
4
C.
5
D.
3
II. TỰ LUẬN (2 điểm)
Câu 21: (0,5 điểm) Xét tính chẵn, lẻ của hàm số
2
cos3
sin 1
x
f x
x
.
Câu 22: (1,5 điểm) Giải các phương trình sau:
a.
cos2 cosx x
b.
3 cos sin 0
x x
c.
8cos 2 .sin 2 .cos4 2
x x x
------------------- HẾT -------------------
| 1/2
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT CHUYÊN
ĐỀ KIỂM TRA MỘT TIẾT - HỌC KÌ I (2019 – 2020) HÙNG VƯƠNG
MÔN: TOÁN – LỚP 11 (SỐ 1) TỔ TOÁN
Thời gian: 45 phút (20 câu TN - 4 câu TL) Mã đề 114
Họ tên học sinh: ..................................................................... Số báo danh: .........................
I. TRẮC NGHIỆM (8 điểm)
Câu 1: Trong các hàm số sau, hàm số nào là hàm số tuần hoàn?
A. y  sin x  cos x x
B. y  3x  2 sin x C. 2
y x sin x
D. y  sin 2x  cos x
Câu 2: Phương trình 3 sin x  cos x  1 tương đương với phương trình nào sau đây?       1    1    1 A. sin x   1   B. sin  x    C. sin x     D. cos x      6   6  2  6  2  3  2 Câu 3: Phương trình 2 2 sin x  4 sin .
x cos x  3cos x  0 có tập nghiệm trùng với tập nghiệm của phương trình nào sau đây? A. cos x  0 B. cot x  1 C.  tan x   1 3cot x   1  0 D. tan x  3
Câu 4: Trong các phương trình sau, phương trình nào vô nghiệm? 2019 A. cos x  B. cot x  2020 C. sin x   D. tan x  2019 2020 Câu 5: Phương trình  x   2 3 tan 1 sin x   1  0 có nghiệm là     A. x    k B. x   k C. x    k 2 D. x   k 2 6 6 6 3
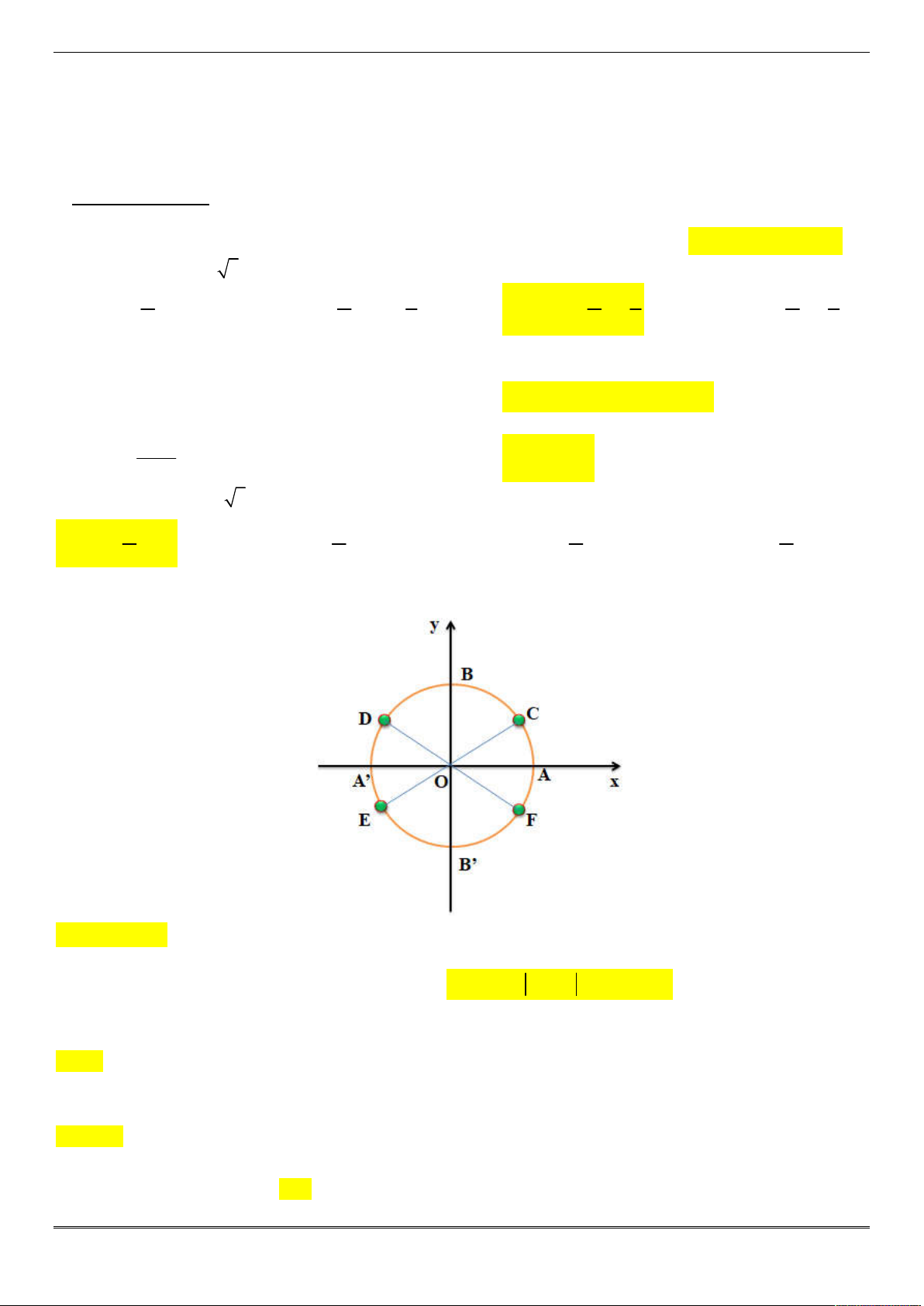
Câu 6: Nghiệm của phương trình 2 sin x 1  0 được biểu diễn trên đường tròn lượng giác ở hình bên dưới là những điểm nào?
A. Điểm C, D
B. Điểm D, E
C. Điểm E, F
D. Điểm C, F
Câu 7: Trong các hàm số sau, hàm số nào là hàm số chẵn?
A. y  2018 cos x  2019 sin x
B. y  sin 2019x  2020 cos x
C. y  tan 2019x  cot 2020x
D. y  cot 2018x  2019 sin x
Câu 8: Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y  3sin x  4 cos x 1. A. 2 B. 3 C. 3 D. 2
Câu 9: Tính giá trị của biểu thức P  3  sin 4x , biết rằng x là nghiệm của phương trình
sin x cos x  2sin x  cos x  2 . A. P  3 B. P  2 C. P  1 D. P  0
Câu 10: Tập giá trị của hàm số 2
y  1 2 sin x cos x  cos 2x là T   ;
a b. Tính tổng 4a b . A. 0 B. 1 C. 1 D. 2 Trang 1/2   
Câu 11: Hàm số nào sau đây có tính đơn điệu trên khoảng 0; 
 khác với các hàm số còn lại?  2 
A. y  2 sin x
B. y  4 tan x
C. y  3cos x
D. y   cot x 3  2 cos x
Câu 12: Tìm điều kiện xác định của hàm số y  . sin xk A. x
k , k   B. x  , k  
C. x k 2 , k  
D. x k , k   2 2
Câu 13: Nghiệm của phương trình cos 2x  5sin x  3  0 là  7  7 A. x  
k 2 , x
k 2 k   B. x    k , x
k k   3 3 6 6  7  7 C. x  
k 2 , x
k 2 k   D. x    k , x
k k   6 6 3 3     3 
Câu 14: Cho phương trình sin 2x   sin x    
 . Tính tổng các nghiệm thuộc khoảng 0;  của  4   4  phương trình.  3 7 A.  B. C. D. 4 2 2
Câu 15: Cho phương trình 3cos x  cos 2x  cos 3x 1  2 sin .
x sin 2x . Gọi  là nghiệm lớn nhất thuộc   
khoảng 0; 2  của phương trình. Tính sin     .  4  2 2 A. 1 B. 0 C.  D. 2 2 sin x 1 Câu 16: Phương trình  có bao nhiêu nghiệm? x 2 A. 3 nghiệm B. 2 nghiệm C. Vô số nghiệm D. Vô nghiệm
Câu 17: Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 2
y  5  2m sin x  m   1 cos 2x xác định trên  ? A. 2 B. 3 C. 4 D. 5       5   
Câu 18: Cho phương trình cos 2 x   4 cos  x      . Khi đặt t  cos  x
 , phương trình đã cho  3   6  2  6 
trở thành phương trình nào sau đây? A. 2
4t  8t  3  0 B. 2
4t  8t  3  0 C. 2
4t  8t  5  0 D. 2
4t  8t  5  0
Câu 19: Có bao nhiêu giá trị nguyên của tham số m để phương trình 2
cos x  cos x m m có nghiệm? A. 2 B. 4 C. 5 D. 3 m sin x 1
Câu 20: Cho hàm số y
. Có bao nhiêu giá trị nguyên âm của tham số m thuộc đoạn  5  ;  5 để cos x  2
giá trị lớn nhất của hàm số lớn hơn 2? A. 6 B. 4 C. 5 D. 3 II. TỰ LUẬN (2 điểm) cos 3x
Câu 21: (0,5 điểm) Xét tính chẵn, lẻ của hàm số f x  . 2 sin x 1
Câu 22: (1,5 điểm) Giải các phương trình sau:
a. cos 2x  cos x
b. 3 cos x  sin x  0 c. 8 cos 2 . x sin 2 . x cos 4x  2
------------------- HẾT ------------------- Trang 2/2