Đề kiểm tra giữa HK2 Toán 11 năm 2018 – 2019 trường Việt Nam – Ba Lan – Hà Nội

Đề kiểm tra giữa HK2 Toán 11 năm 2018 – 2019 trường Việt Nam – Ba Lan – Hà Nội mã đề 395 gồm 05 trang với 50 câu trắc nghiệm, thời gian làm bài thi Toán là 90 phút, kỳ thi được diễn ra vào thứ Ba ngày 05 tháng 03 năm 2019

58 29 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 11

Môn: Toán 11

Thông tin:

32 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 1 Mã đề 1881
GIẢI CHI TIẾT ĐỀ GIỮA HỌC KỲ II
MÔN TOÁN – KHỐI 11 - 2018 - 2019
TRƯỜNG THPT VIỆT NAM - BA LAN
Câu 1. Tìm
m
để hàm số
( )
3
3
12
3
x
khi x
fx
x
m khi x
−
=
+−
=
liên tục trên tập xác định.
A.
2m =
. B.
4m =
. C.
0m =
. D.
1m =
.
Câu 2. Tính tổng:
A.
3
7
. B.
5
7
. C.
11
7
. D.
7
3
.
Câu 3. Cho phương trnh . Mnh đ no sau đây l đng ?
A. Phương trnh không c nghim thuc khong .
B. Phương trnh c t nht hai nghim thuc khong .
C. Phương trnh không c nghim thuc khong .
D. Phương trnh c đng mt nghim thuc khong .
Câu 4. Tm khng định đng:
A. . B. . C. , . D. .
Câu 5. Biết
1
3
lim
1
x
xa
x
+
→−
+
=−
+
thì giá trị của
a
thỏa mãn
A.
3a −
. B.
3a −
. C.
3a
. D.
5a
.
Câu 6. Cho
2
8 1 4 3
lim 2
3
nn
ab
n
+ + −
=+
+
. Mnh đ đng l
A.
3ab=
. B.
33ab+ +
. C.
23ab+=
. D.
2ab+
.
Câu 7. Tìm h thức liên h giữa các số thực
, ab
để
(
)
22
lim 3 1 1n an n bn+ + − + − =
.
A.
2ab+=
. B.
1ab+=
. C.
2ab−=
. D.
1ab−=
.
Câu 8. Cho tứ din đu
, ABCD M
l trung điểm của cạnh
AB
. Khi đ gc giữa hai vectơ
, AB CM
bằng:
A.
90
. B.
45
. C.
120
. D.
60
.
Câu 9. Chọn mnh đ đng trong các mnh đ sau:
Trong không gian
A. Ba véctơ đồng phng khi và chỉ khi ba véc tơ phi nằm trong cùng mt mặt phng.
5 4 2
7 3 2 0x x x− + + =
( )
0;2
( )
1;3−
( )
1;1−
( )
1;2−
4
lim
x
x
→−
= −
3
lim
x
x
→−
= +
lim 0
x
x
q
→+
=
( )
1q
0
0
lim
xx
xx
→
=
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 2 Mã đề 1881
B. Ba véctơ đồng phng khi và chỉ khi giá của ba véctơ đ song song với nhau .
C. Ba véctơ đồng phng khi và chỉ khi ba véctơ cùng hướng.
D. Ba véctơ đồng phng khi và chỉ khi giá của ba véctơ cùng song song với mt mặt phng
Câu 10. Cho hình chóp
.S ABC
có
( )
⊥SA ABC
và
⊥AB BC
. Gọi
H
là hình chiếu vuông góc của
A
lên
SB
khng định no sau đây l đng?
A.
⊥AH SC
. B.
⊥AH AC
. C.
⊥AH AB
. D.
( )
⊥AH SAC
.
Câu 11. Tính giới hạn của dãy số
( )
1 1 1
...
2 1 2 3 2 2 3 1 1
n
u
n n n n
= + + +
+ + + + +
A.
4
5
. B.
2
3
. C.
1
. D.
3
2
.
Câu 12. Dãy số no sau đây c giới hạn bằng
0
?
A.
2
4nn−
. B.
2
3
1
nn
n
−
+
. C.
6
5
n



. D.
2
3
n

−


.
Câu 13. Cho các khng định:
(I) Cho hàm số
( )
y f x=
liên tục trên
;ab
và
( ) ( )
.0f a f b
. Khi đ phương trnh
( )
0fx=
có ít nht mt nghim trên khong
( )
;ab
.
(II) Cho hàm số
( )
y f x=
liên tục trên
;ab
và
( ) ( )
.0f a f b
. Khi đ phương trnh
( )
0fx=
không có nghim trên khong
( )
;ab
.
Trong các khng định trên:
A. Chỉ (I) đng. B. C (I), (II) đng. C. C (I), (II) sai. D. Chỉ (II) đng.
Câu 14. Cho hàm số
( )
fx
c đồ thị như hnh vẽ
Chọn đáp án đng
A. Hàm số
( )
fx
gián đoạn tại
1x =−
.
B. Hàm số
( )
fx
liên tục tại
1x =−
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 3 Mã đề 1881
C. Hàm số
( )
fx
liên tục trên khong
( )
3;1−
.
D. Hàm số
( )
fx
liên tục trên .
Câu 15. TCho hình hp
.ABCD A B C D
. Mt đường thng
cắt các đường thng
,,AA BC C D
lần
lượt tại
,,M N P
sao cho
3NM NP=
. Tính
MA
k
MA
=
.
A.
2
3
k =
. B.
2k =
. C.
3k =
. D.
2
3
k =
.
Câu 16. Cho
,uv
bt kì, chọn mnh đ đng?
A.
( )
.
cos ,
.
uv
uv
uv
=
. B.
( )
. . .cos ,u v u v u v=
. C.
( )
. . .cos ,u v u v u v=
.D.
( )
.
cos ,
.
uv
uv
uv
=
.
Câu 17.
( )
2018 2019
lim 4 nn−−
bằng
A.
0
. B.
−
. C.
2019−
. D.
+
.
Câu 18. Cho hình chóp tứ giác
.S ABCD
, c đáy
ABCD
là hình vuông cạnh
a
, các cạnh bên đu bằng
2a
. Góc giữa cạnh bên
SB
và mặt phng
( )
ABCD
bằng
A.
0
30
. B.
0
60
. C.
0
90
. D.
0
45
.
Câu 19. Rút gọn
2 4 6 2
1 sin sin sin ... sin ...
n
S x x x x= + + + + + +
với
sin 1x 
.
A.
2
cosSx=
. B.
2
tanSx=
. C.
2
1
1 sin
S
x
=
+
. D.
2
1 tanSx=+
.
Câu 20.
lim 3 5 7 ... 2019
x
a
x x x x x x
b
→+


+ + + + − =


(với
a
,
b
nguyên dương nhỏ nht). Tính
ab+
.
A.
6
. B.
5
. C.
3
. D.
4
.
Câu 21. Tìm
a
để hàm số
2
32
2
()
2
52
xx
khi x
fx
x
ax a khi x
−+
=
−
+ −
liên tục trên R.
A. 1. B. 3. C. 0. D. 2.
Câu 22. Cho hàm số
11
0
()
1
0
2
x
khi x
x
fx
khi x
+−
=
=
. Chọn khng định đng?
A. Hàm số gián đoạn tại
0x =
. B. Hàm số liên tục trên R.
C. Hàm số liên tục trên
)
1;− +
. D. Hàm số liên tục trên
( )
3,2−
.
Câu 23. Cho hình chóp
.S ABC
có
2SA SB SC AB AC a= = = = =
và
2BC a=
. Khi đ gc giữa hai
đường thng
AC
và
SB
bằng
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 4 Mã đề 1881
A.
30
. B.
90
. C.
45
. D.
60
.
Câu 24. Cho hình chóp
.S ABCD
c đáy l hnh vuông
ABCD
và
SA
vuông góc với mặt phng đáy
( )
ABCD
. Mt mặt phng
( )
đi qua
A
và vuông góc với
SC
cắt hình chóp theo thiết din là:
A. hình thoi có mt góc có số đo bằng
60
. B. hình vuông.
C. hình bình hành. D. tứ giác c hai đường chéo vuông góc.
Câu 25. Cho tứ din
ABCD
. Gọi
,,M N G
lần lượt l trung điểm của
,,AB CD MN
. Chọn khng định
đng:
A.
2GA GB GC GD MN+ + + =
. B.
( )
1
2
MN AD CB=+
.
C.
( )
1
2
MN AC BD=+
. D.
( )
1
2
MN AB CD=+
Câu 26.
3
2
1
5 3 3 5 1
lim
1
x
xx
x m n
→
+ − +
=−
−
( với
,mn
là các số nguyên dương). Tnh
mn−
?
A. 15. B. 14. C. 12. D. 16.
Câu 27. Cho hình lập phương
.ABCD EFGH
. Hãy xác định góc giữa cặp véctơ
AC
và
DE
?
A.
120
. B.
45
. C.
60
. D.
90
.
Câu 28.
3
5
lim
3
x
x
x
−
→
+
−
bằng
A.
15
2
−
. B.
−
. C.
1
. D.
+
.
Câu 29. Cho tứ din đu
ABCD
cạnh
a
. Góc giữa
AB
và
CD
bằng:
A.
0
60 .
B.
0
30 .
C.
0
90 .
D.
0
45 .
Câu 30. Tìm
m
để hàm số
2
20
()
10
x m khi x
fx
x x khi x
+
=
+ +
liên tục tại
0x =
A.
1
.
4
m =
B.
1.m =
C.
1
.
2
m =
D.
0.m =
Câu 31.
(
)
2
lim 3
x
x x x
→+
+−
bằng
A.
+
. B.
3
2
. C.
3
. D.
0
.
Câu 32. Tìm khng định sai trong các khẳng định sau :
A.
G
là trọng tâm tam giác
ABC
0GA GB GC + + =
.
B.
I
l trung điểm của
AB
2MA MB MI + =
,
M
.
C.
G
là trọng tâm tam giác
ABC
3MA MB MC MG + + =
,
M
.
D.
. ' ' ' 'ABCD A B C D
là hình hp. Khi đ ta c :
'AB AD AA AC+ + =
.
Câu 33.
2
3
lim( 4)
x
x
→
−
bằng:
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 5 Mã đề 1881
A.
2
. B.
1
. C.
4−
. D
1−
.
Câu 34. Cho lăng trụ tam giác
.ABC A B C
có
' , ,AA a AB b AC c= = =
.Hãy biểu diễn vectơ
BC
theo các vectơ
, , .a b c
A.
B C a b c
= + −
B.
B C a b c
= − + −
. C.
B C a b c
= − +
D.
B C a b c
= − +
.
Câu 35.
( )( )( ) ( )
0
1 1 2 1 3 ... 1 2019 1
lim
x
x x x x
x
→
+ + + + −
bằng
A.
2018.2019
. B.
1009.2019
. C.
1010.2019
. D.
0
.
Câu 36. Biết hàm số
( ) ( )
2
2
khi 1
1
,
1
khi 1
2
x ax b
x
x
f x a b R
x
++
−
=
−=
liên tục tại
1x =
. Hãy tính
25S a b=+
A.
10S =
. B.
7S =
. C.
4S =
. D.
2S =
.
Câu 37.
2
1
32
lim
1
x
xx
x
→
−+
−
bằng
A.
1−
. B.
2−
C. 2. D. 1.
Câu 38. Cho
()fx
liên tục trên
1;5−
thỏa mãn
( 1) 1f −=
,
(5) 6f =
. Phương trnh no sau đây luôn c
nghim trong khong
( 1;5)−
?
A.
( ) 8fx=
. B.
( ) 3fx=
. C.
( ) 5 0fx+=
. D.
( ) 1fx=
.
Câu 39. Giá trị của
(
)
2
lim 4 5 1 2n n n+ + −
bằng :
A.
−
. B.
5
2
. C.
+
. D.
5
4
.
Câu 40.
( )
24
lim 5 3 2019
x
xx
→−
−−
bằng
A.
−
. B.
3−
. C.
2019−
. D.
+
.
Câu 41. Cho hình chóp
.S ABCD
c đáy
ABCD
là hình thoi tâm
O
. Biết
,SA SC SB SD==
. Khng
định no sau đây sai?
A.
( )
SO ABCD⊥
B.
( )
AC SBD⊥
C.
( )
BD SAC⊥
D.
( )
AB SAD⊥
Câu 42. Cho hình chóp
.S ABC
, c đáy
ABC
l tam giác đu cạnh
a
. Gọi
O
l tâm đường tròn ngoại
tiếp tam giác
ABC
. Biết
SO
vuông góc với đáy
( )
ABC
và
2SO a=
. Gọi
M
l điểm thuc
đường cao
AH
của tam giác
ABC
. Xét mặt phng
( )
P
đi qua
M
và vuông góc với
AH
. Đặt
3
,
3
a
AM x x=
. Xác định vị tr điểm
M
để thiết din của hình chóp cắt bởi mặt phng
( )
P
có din tích lớn nht. Khi đ tỷ số
AM
AH
bằng
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 6 Mã đề 1881
A.
4
5
AM
AH
=
B.
5
6
AM
AH
=
C.
3
4
AM
AH
=
D.
2
3
AM
AH
=
Câu 43. [Mc đ 2]
0
5 3 3
lim
x
xa
x
bc
→
+−
=
(với
,,abc
). Tnh
a b c−+
.
A. 0. B. 6. C. 8. D. 4.
Câu 44.
( )
3
lim 2018 2 5
x
xx
→−
− + +
bằng
A.
+
. B. 0. C.
−
. D.
2018−
.
Câu 45. Hàm số
( )
2
43
2
−+
=
−
xx
fx
x
.không liên tục tại
A.
3=x
. B.
2=x
. C.
1=x
. D.
0=x
.
Câu 46.
13
lim
25
→−
−
+
x
x
x
.bằng
A.
3
2
−
. B.
1
5
. C.
1
2
. D.
3
5
−
.
Câu 47. Giá trị của
2
23
lim
32
n
nn
+
−+
bằng:
A.
1
. B.
2
3
. C.
+
. D.
0
.
Câu 48. Cho hai đường thng phân bit
a
,
b
v điểm
O
không thuc mặt phng
( )
P
. Mnh đ nào
sau đây l sai ?
A. Nếu hai đường thng
a
và
b
cùng vuông góc với mặt phng
( )
P
thì chúng song song với
nhau.
B. Nếu
//ab
và
a
vuông góc với mặt phng
( )
P
thì
b
cũng vuông gc với mặt phng
( )
P
.
C. Có duy nht mt đường thng
d
đi qua điểm
O
và song song với mặt phng
( )
P
.
D. Có duy nht mt đường thng
d
đi qua điểm
O
và vuông góc với mặt phng
( )
P
.
Câu 49.
2
10 30
lim
5.30 4.20
nn
nn
+
+
−
bằng
A.
+
. B.
−
. C.
900
. D.
180
.
Câu 50. Cho hình chóp
.S ABCD
c đáy
ABCD
là hình vuông cạnh
a
,
2SA a=
và
SA
vuông góc
với mặt phng đáy
( )
ABCD
. Gọi
là góc giữa
SB
và mặt phng
( )
SAC
. Tính
tan
.
A.
1
tan
5
=
. B.
1
tan
3
=
. C.
tan 2
=
. D.
1
tan
2
=
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 7 Mã đề 1881
GIẢI CHI TIẾT ĐỀ GIỮA HỌC KỲ II
MÔN TOÁN – KHỐI 11 - 2018 - 2019
TRƯỜNG THPT VIỆT NAM - BA LAN
Câu 1. Tìm
m
để hàm số
( )
3
3
12
3
x
khi x
fx
x
m khi x
−
=
+−
=
liên tục trên tập xác định.
A.
2m =
. B.
4m =
. C.
0m =
. D.
1m =
.
Lời giải
Chọn B
Tác giả: Trần Công Diêu; Fb: Trần Công Diêu
Ta có:
( )
( )
( )
( )
3 3 3
3 1 2
3
lim lim lim 4
3
12
x x x
xx
x
fx
x
x
→ → →
− + +
−
= = =
−
+−
và
( )
3fm=
.
Để hàm số liên tục trên tập xác định thì
( ) ( )
3
lim 3 4
x
f x f m
→
= =
.
Câu 2. Tính tổng:
( ) ( ) ( )
23
0,3 0,3 0,3 ... 0,3 ...
n
S = + + + + +
A.
3
7
. B.
5
7
. C.
11
7
. D.
7
3
.
Lời giải
Chọn A
Tác giả: Trần Công Diêu; Fb: Trần Công Diêu
Ta có dãy số
( ) ( ) ( ) ( )
23
0,3 ; 0,3 ; 0,3 ;...; 0,3 ;...
n
là dãy cp số nhân lùi vô hạn với số hạng đầu
tiên là
1
0,3u =
và công bi
0,3q =
1
0,3 3
1 1 0,3 7
u
S
q
= = =
−−
.
Câu 3. Cho phương trnh
5 4 2
7 3 2 0x x x− + + =
. Mnh đ no sau đây l đng ?
A. Phương trnh không c nghim thuc khong
( )
0;2
.
B. Phương trnh c t nht hai nghim thuc khong
( )
1;3−
.
C. Phương trnh không c nghim thuc khong
( )
1;1−
.
D. Phương trnh c đng mt nghim thuc khong
( )
1;2−
.
Lời giải
Tác giả:Nguyn Anh Tun ; Fb:Nguyn Ngc Minh Châu
Chọn B
Xét hm số
( )
5 4 2
7 3 2f x x x x= − + +
liên tục trên .
Ta c:
( )
13f − = −
;
( )
02f =
;
( )
11f =−
( ) ( )
1 . 0 0ff −
v
( ) ( )
0 . 1 0ff
. Do đ
phương trnh
5 4 2
7 3 2 0x x x− + + =
c t nht mt nghim thuc khong
( )
1;0−
v t nht mt
nghim thuc khong
( )
0;1
nên phương trnh c t nht hai nghim thuc khong
( )
1;3−
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 8 Mã đề 1881
Câu 4. Tm khng định đng:
A.
4
lim
x
x
→−
= −
. B.
3
lim
x
x
→−
= +
. C.
lim 0
x
x
q
→+
=
,
( )
1q
. D.
0
0
lim
xx
xx
→
=
.
Lời giải
Tác giả:Nguyn Anh Tun ; Fb:Nguyn Ngc Minh Châu
Chọn D
A sai v
4
lim
x
x
→−
= +
; B sai v
3
lim
x
x
→−
= −
; C sai v
lim 1
x
x
q
→+
khi
1q
v D đng.
Câu 5 . Biết
1
3
lim
1
x
xa
x
+
→−
+
=−
+
thì giá trị của
a
thỏa mãn
A.
3a −
. B.
3a −
. C.
3a
. D.
5a
.
Lời giải
Tác giả: Nguyn Tuyết Lê ; Fb: Nguyen Tuyet Le
Chọn C
Ta có
( )
1
lim 3 3
x
x a a
+
→−
+ = − +
;
( )
1
lim 1 0
x
x
+
→−
+=
;
10x +
với
1x −
.
Lại do
1
3
lim
1
x
xa
x
+
→−
+
=−
+
nên
30a− +
3a
.
Câu 6. Cho
2
8 1 4 3
lim 2
3
nn
ab
n
+ + −
=+
+
. Mnh đ đng l
A.
3ab=
. B.
33ab+ +
. C.
23ab+=
. D.
2ab+
.
Lời giải
Tác giả: Nguyn Tuyết Lê ; Fb: Nguyen Tuyet Le
Chọn B
Ta có
2
8 1 4 3
lim
3
nn
n
+ + −
+
2
14
83
lim
3
1
n
nn
n
n

+ + −


=

+


2
14
83
lim
3
1
nn
n
+ + −
=
+
2 2 3=−
.
Do đ
2a =
;
3b =−
.
Đáp án A, C, D sai.
Câu 7. Tìm h thức liên h giữa các số thực
, ab
để
(
)
22
lim 3 1 1n an n bn+ + − + − =
.
A.
2ab+=
. B.
1ab+=
. C.
2ab−=
. D.
1ab−=
.
Lời giải
Tác giả:Nguyn Thành Đô ; Fb: Thành Đô Nguyn
Chọn C
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 9 Mã đề 1881
Xét
(
)
( )
22
22
22
4
4
lim 3 1 lim lim
31
31
11
.
2
ab
a b n
n
n an n bn
ab
n an n bn
n n n n
ab
−+
−+
+ + − + − = =
+ + + + −
+ + + + −
−
=
Theo gi thiết:
1 2.
2
ab
ab
−
= − =
Câu 8. Cho tứ din đu
, ABCD M
l trung điểm của cạnh
AB
. Khi đ gc giữa hai vectơ
, AB CM
bằng:
A.
90
. B.
45
. C.
120
. D.
60
.
Lời giải
Tác giả:Nguyn Thành Đô ; Fb: Thành Đô Nguyn
Chọn A
Vì tam giác
ABC
đu nên:
( )
, 90 .AB CM AB CM AB CM⊥ ⊥ =
Câu 9. Chọn mnh đ đng trong các mnh đ sau:
Trong không gian
A. Ba véctơ đồng phng khi và chỉ khi ba véc tơ phi nằm trong cùng mt mặt phng.
B. Ba véctơ đồng phng khi và chỉ khi giá của ba véctơ đ song song với nhau .
C. Ba véctơ đồng phng khi và chỉ khi ba véctơ cùng hướng.
D. Ba véctơ đồng phng khi và chỉ khi giá của ba véctơ cùng song song với mt mặt phng
Lời giải
Tác giả: Nguyn Thành Trung ; Fb:Nguyn Thành Trung
Chọn D
Theo định nghĩa 3 véctơ gọi l đồng phng nếu các giá của chúng cùng song song với mt mặt
phng.
Câu 10. Cho hình chóp
.S ABC
có
( )
⊥SA ABC
và
⊥AB BC
. Gọi
H
là hình chiếu vuông góc của
A
lên
SB
khng định no sau đây l đng?
A.
⊥AH SC
. B.
⊥AH AC
. C.
⊥AH AB
. D.
( )
⊥AH S AC
.
Lời giải
Tác giả: Nguyn Thành Trung ; Fb:Nguyn Thành Trung
Chọn A
M
D
C
B
A
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 10 Mã đề 1881
Ta có
( )
⊥
⊥
⊥
BC AB
BC SAB
BC SA
Suy ra
( )
AH SB
AH SBC AH AC
AH BC
⊥
⊥ ⊥
⊥
.
Câu 11. Tính giới hạn của dãy số
( )
1 1 1
...
2 1 2 3 2 2 3 1 1
n
u
n n n n
= + + +
+ + + + +
A.
4
5
. B.
2
3
. C.
1
. D.
3
2
.
Lời giải
Tác giả:Phạm Văn Tun ; Fb: Phạm Tun
Chọn C
Ta có:
( )
( )
( )( )
( )
11
1 1 1 1
1 1 1
1 1 1 1
n n n n
nn
n n n n n n
n n n n n n n n
+ + + −
+−
= = = −
+ + + +
+ + + + + +
.
Áp dụng kết qu trên cho
n
u
ta được:
1 1 1 1 1 1 1
... 1
1 2 2 3 1 1
n
u
n n n
= − + − + + − = −
++
.
Khi đ
1
lim lim 1
1
n
u
n

=−

+

.
Mà
lim1 1=
và
11
.
10
lim lim lim 0
1
1 1 1
11
n
nn
n
n
nn
= = = =
+
++
. Vậy
lim 1
n
u =
.
Câu 12. Dãy số no sau đây c giới hạn bằng
0
?
A.
2
4nn−
. B.
2
3
1
nn
n
−
+
. C.
6
5
n



. D.
2
3
n

−


.
Lời giải
Tác giả:Phạm Văn Tun ; Fb:Phạm Tun
A
C
B
S
H
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 11 Mã đề 1881
Chọn D
Ta có
lim 0
n
n
q
→+
=
nếu
1q
. Do đ
2
lim 0
3
n
n→+

−=


.
Câu 13. Cho các khẳng định:
(I) Cho hàm số
( )
y f x=
liên tục trên
;ab
và
( ) ( )
.0f a f b
. Khi đ phương trnh
( )
0fx=
có ít nht mt nghim trên khong
( )
;ab
.
(II) Cho hàm số
( )
y f x=
liên tục trên
;ab
và
( ) ( )
.0f a f b
. Khi đ phương trnh
( )
0fx=
không có nghim trên khong
( )
;ab
.
Trong các khng định trên:
A. Chỉ (I) đúng. B. Cả (I), (II) đúng. C. Cả (I), (II) sai. D. Chỉ (II) đúng.
Lời giải
Chọn A
(I) Đng theo định lý 3 – SGK tr 138.
(II) Sai. Vì ví dụ như hm số
( )
2
1f x x=−
liên tục trên
2;2−
và
( ) ( )
2 . 2 9 0ff− =
nhưng
( )
0fx=
có nghim
( )
1,1 2;2− −
.
Câu 14. Cho hàm số
( )
fx
có đồ thị như hình vẽ
Chọn đáp án đúng
A. Hàm số
( )
fx
gián đoạn tại
1x =−
.
B. Hàm số
( )
fx
liên tục tại
1x =−
.
C. Hàm số
( )
fx
liên tục trên khoảng
( )
3;1−
.
D. Hàm số
( )
fx
liên tục trên .
Lời giải
Chọn A
Nhn vo đồ thị ta thy tại
1x =−
đồ thị hàm số bị gián đoạn.
Câu 15. TCho hình hộp
.ABCD A B C D
. Một đường thẳng
cắt các đường thẳng
,,AA BC C D
lần lượt
tại
,,M N P
sao cho
3NM NP=
. Tính
MA
k
MA
=
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 12 Mã đề 1881
A.
2
3
k =
. B.
2k =
. C.
3k =
. D.
2
3
k =
.
Lời giải
Tác giả: Trương Thanh Nhàn; Fb: Trương Thanh Nhàn.
Chọn D
Gi sử
,MA mAA
=
,NB nBC=
PC pD C
=
với
,,m n p
.
Ta có:
NB nBC NA AB nAD NA AB nAD= + = = − +
( )
1PC pD C PA AC pAB PA AC pAB PA AA p AB AD
= + = = − + = − + − −
NM NA MA mAA AB nAD
= − = − − +
NP NA MA mAA AB nAD
= − = − − +
( )
3 3 3 3 1NM NP mAA AB nAD AA pAB n AD

= − − + = − + +
(1)
Do
;AA
;AB
AD
l các vectơ không đồng phng nên
( )
( )
3
3
1
1 1 3
3
31
3
2
m
m
pp
nn
n
=−
−=
− = − =


=+
=−
Do đ
3 3 3
3
2 2 2
MA AA MA MA MA MA k
= − = = =
.
Câu 16. Cho
,uv
bất kì, chọn mệnh đề đúng?
M
P
N
D'
C'
B'
D
C
B
A'
A
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 13 Mã đề 1881
A.
( )
.
cos ,
.
uv
uv
uv
=
. B.
( )
. . .cos ,u v u v u v=
. C.
( )
. . .cos ,u v u v u v=
.D.
( )
.
cos ,
.
uv
uv
uv
=
.
Lời giải
Tác giả: Trương Thanh Nhàn; Fb: Trương Thanh Nhàn.
Chọn B
Dựa vo định nghĩa ta c ngay đáp án B đng.
Câu 17.
( )
2018 2019
lim 4 nn−−
bằng
A.
0
. B.
−
. C.
2019−
. D.
+
.
Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ
Chọn B
Ta có
( )
2018 2019 2019
2019
41
lim 4 lim . 1n n n
nn


− − = − −




.
Vì
2019
limn = +
và
2019
41
lim 1 1 0
nn

− − = −


nên
2019
2019
41
lim . 1n
nn


− − = −




.
Câu 18. Cho hình chóp tứ giác
.S ABCD
, c đáy
ABCD
là hình vuông cạnh
a
, các cạnh bên đu bằng
2a
. Góc giữa cạnh bên
SB
và mặt phng
( )
ABCD
bằng
A.
0
30
. B.
0
60
. C.
0
90
. D.
0
45
.
Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ
Chọn D
Gọi
O
l giao điểm của
AC
và
BD
. Tam giác
SAC
cân tại
S
và
O
l trung điểm của
AC
nên
SO AC⊥
. Tương tự ta có
SO BD⊥
.
( )
( )
,
SO AC
SO BD
SO ABCD
AC BD ABCD
AC BD O
⊥
⊥
⊥
=
.
O
D
A
C
B
S
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 14 Mã đề 1881
Suy ra
BO
là hình chiếu vuông góc của
BS
trên mặt phng
( )
ABCD
.
Do đ
( )
( )
( )
,,SB ABCD SB BO SBO==
. Ta có
2
22
BD a
BO ==
.
Tam giác
SBO
vuông tại
O
nên
0
2
1
2
cos 60
2
2
a
BO
SBO SBO
SB
a
= = = =
.
Câu 19. Rút gọn
2 4 6 2
1 sin sin sin ... sin ...
n
S x x x x= + + + + + +
với
sin 1x 
.
A.
2
cosSx=
. B.
2
tanSx=
. C.
2
1
1 sin
S
x
=
+
. D.
2
1 tanSx=+
.
Lời giải
Tác giả: Nguyn Đức Hoạch; Fb: Hoạch Nguyn
Chọn D
Ta có:
2
sin 1x
với mọi
sin 1x 
.
2 4 6 2
1 sin sin sin ... sin ...
n
S x x x x = + + + + + +
chính là tổng của cp số nhân lùi vô hạn với
công bi
2
sinqx=
và
1
1u =
.
2
1
22
11
tan 1
1 1 sin cos
u
Sx
q x x
= = = = +
−−
.
Câu 20.
lim 3 5 7 ... 2019
x
a
x x x x x x
b
→+


+ + + + − =


(với
a
,
b
nguyên dương nhỏ nht). Tính
ab+
.
A.
6
. B.
5
. C.
3
. D.
4
.
Lời giải
Chọn B
Ta có:
lim 3 5 7 ... 2019
x
x x x x x x
→+


+ + + + −


3 5 7 ... 2019
lim
3 5 7 ... 2019
x
x x x x x x
x x x x x x
→+


+ + + + −
=



+ + + + +

3 5 7 ... 2019
lim
3 5 7 ... 2019
x
x x x x
x x x x x x
→+


+ + +
=



+ + + + +

1009
1010
3
21
37
21
5 7 2019
3 ...
3
lim
2
3 5 7 2019
1 ... 1
x
xx
x
x x x
x
−
→+
−


+ + + +


==


+ + + + + +



.
3a=
,
2b =
5ab + =
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 15 Mã đề 1881
Câu 21. Tìm
a
để hàm số
2
32
2
()
2
52
xx
khi x
fx
x
ax a khi x
−+
=
−
+ −
liên tục trên R.
A. 1. B. 3. C. 0. D. 2.
Lời giải
Tác giả: Tạ Minh Trang; Fb: Minh Trang
Chọn D
Với
( )
;2x −
,
2
32
()
2
xx
fx
x
−+
=
−
liên tục trên
( )
;2−
.
Với
( )
2;x +
,
( ) 5f x ax a= + −
liên tục trên
( )
2;+
.
Với
2x =
, ta có
(2) 3 5fa=−
và
( )
22
lim ( ) lim 5 3 5
xx
f x ax a a
++
→→
= + − = −
;
( )( )
( )
2
2 2 2 2
12
32
lim ( ) lim lim lim 1 1
22
x x x x
xx
xx
f x x
xx
− − − −
→ → → →
−−
−+
= = = − =
−−
.
Hàm số
()fx
liên tục trên R
3 5 1 2aa − = =
.
Câu 22. Cho hàm số
11
0
()
1
0
2
x
khi x
x
fx
khi x
+−
=
=
. Chọn khng định đng?
A. Hàm số gián đoạn tại
0x =
. B. Hàm số liên tục trên R.
C. Hàm số liên tục trên
)
1;− +
. D. Hàm số liên tục trên
( )
3,2−
.
Lời giải
Tác giả: Tạ Minh Trang; Fb: Minh Trang
Chọn C
Với
( )
1;0 (0; )x − +
,
11
()
x
fx
x
+−
=
liên tục trên khong
( )
1;0 (0; )− +
.
Với
1
0, (0)
2
xf==
và
( )
0 0 0 0
1 1 1 1 1 1
lim ( ) lim lim lim
2
11
11
x x x x
xx
fx
x
x
xx
→ → → →
+ − + −
= = = =
++
++
.
Do đ hm số liên tục tại
0x =
.
Mặt khác
11
11
lim ( ) lim 1
xx
x
fx
x
++
→− →−
+−
==
và
( 1) 1f −=
. Suy ra hàm số liên tục phi tại
1−
.
Vậy hàm số liên tục trên
)
1;− +
.
Câu 23. Cho hình chóp
.S ABC
có
2SA SB SC AB AC a= = = = =
và
2BC a=
. Khi đ gc giữa hai
đường thng
AC
và
SB
bằng
A.
30
. B.
90
. C.
45
. D.
60
.
Lời giải
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 16 Mã đề 1881
Tác giả: Phạm Văn Ninh; Fb: Ninh Phạm Văn
Chọn D
Từ gi thiết ta có tam giác
SBC
vuông tại
S
.
Ta có
( )
.AC SB SB SC SA=−
..SB SC SB SA=−
.SB SA=−
2
2
a
=−
.
( )
.
cos ,
.
AC SB
AC SB
AC SB
=
1
2
=−
( )
, 120AC SB =
.
Vây góc giữa giữa hai đường thng
AC
và
SB
bằng
60
.
Câu 24. Cho hình chóp
.S ABCD
c đáy l hnh vuông
ABCD
và
SA
vuông góc với mặt phng đáy
( )
ABCD
. Mt mặt phng
( )
đi qua
A
và vuông góc với
SC
cắt hình chóp theo thiết din là:
A. hình thoi có mt góc có số đo bằng
60
. B. hình vuông.
C. hình bình hành. D. tứ giác c hai đường chéo vuông góc.
Lời giải
Tác giả: Phạm Văn Ninh; Fb: Ninh Phạm Văn
Chọn D
Gọi
O
l giao điểm của
AC
và
BD
. Từ
A
dựng
AC SC
⊥
, gọi
I AC SO
=
.
Vì
BD SA
BD SC
BD AC
⊥
⊥
⊥
, mà
( )
BD
,
( ) ( )
//SC BD

⊥
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 17 Mã đề 1881
Vậy
( )
cắt
( )
SBD
theo giao tuyến đi qua
I
và song song với
BD
cắt
SB
,
SD
lần lượt tại
B
,
D
thiết din của hình chóp cắt bởi
( )
là tứ giác
AB C D
.
Ta có:
( )
( )
//
BD SAC
B D SAC
BD B D
⊥

⊥

,
( )
AC SAC B D AC
⊥
thiết din có hai
đường chéo vuông góc.
Câu 25. Cho tứ din
ABCD
. Gọi
,,M N G
lần lượt l trung điểm của
,,AB CD MN
. Chọn khng định
đng:
A.
2GA GB GC GD MN+ + + =
. B.
( )
1
2
MN AD CB=+
.
C.
( )
1
2
MN AC BD=+
. D.
( )
1
2
MN AB CD=+
Lời giải
Tác giả: Phan Dung ; Fb: dungphan
Chọn C
Ta có:
( ) ( )
2
0 0 2 .
AC BD AM MN NC BM MN ND
AM BM NC ND MN
MN
+ = + + + + +
= + + + +
= + +
( )
1
2
MN AC BD = +
(đpcm).
(,MN
lần lượt l trung điểm của
,AB CD
nên
0, 0)AM BM NC ND+ = + =
.
Câu 26.
3
2
1
5 3 3 5 1
lim
1
x
xx
x m n
→
+ − +
=−
−
( với
,mn
là các số nguyên dương). Tnh
mn−
?
A. 15. B. 14. C. 12. D. 16.
Lời giải
Tác giả: Phan Dung ; Fb: dungphan
Chọn D
( ) ( )
3
33
2 2 2 2
1 1 1 1
5 3 2 3 2
5 3 3 5 3 2 3 2
lim lim lim lim
1 1 1 1
x x x x
xx
x x x x
x x x x
→ → → →
+ − − + −
+ − + + − + −
= = −
− − − −
.
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
3
2
2
1
2
33
1
2
1
33
2
2
1 1 1
51
5 3 2
) lim lim
1
1 5 3 2 5 3 4
55
lim
24
1 5 3 2 5 3 4
3 2 1 1 1
) lim lim lim
18
1 3 2 1 3 2
x
x
x
x x x
x
x
x
x x x
x x x
xx
x
x x x x
→
→
→
→ → →
−
+−
+=
−
− + + + +
==
+ + + + +
+ − −
+ = = =
−
− + + + + +
Nên suy ra:
24, 8 16m n m n= = − =
.
Câu 27 . Cho hình lập phương
.ABCD EFGH
. Hãy xác định góc giữa cặp véctơ
AC
và
DE
?
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 18 Mã đề 1881
A.
120
. B.
45
. C.
60
. D.
90
.
Lời giải
Tác giả: Phan Chí Dũng ; Fb: Phan Chí Dũng
Chọn A
Ta có góc giữa
AC
và
DE
bằng góc giữa
AC
và
CF
.
Dựng
CK AC=
suy ra góc giữa
AC
và
CF
bằng góc giữa
CK
và
CF
bằng góc
FCK
.
Xét tam giác
AFC
, ta có
AC AF FC==
suy ra tam giác
AFC
l tam giác đu, suy ra góc
60 120ACF FCK= =
.
Vậy góc giữa
AC
và
CF
bằng
120
hay góc giữa
AC
và
DE
bằng
120
.
Câu 28 .
3
5
lim
3
x
x
x
−
→
+
−
bằng
A.
15
2
−
. B.
−
. C.
1
. D.
+
.
Lời giải
Tác giả: Phan Chí Dũng ; Fb: Phan Chí Dũng
Chọn B
Ta có
( )
3
lim 3 0
x
x
−
→
−=
và
30x −
với
3x
.
( )
3
lim 5 3 5 8 0
x
x
−
→
+ = + =
. Suy ra
3
5
lim
3
x
x
x
−
→
+
=−
−
.
Câu 29. Cho tứ din đu
ABCD
cạnh
a
. Góc giữa
AB
và
CD
bằng:
A.
0
60 .
B.
0
30 .
C.
0
90 .
D.
0
45 .
Lời giải
Tác giả: Trần Thị Thủy ; Fb: Trần Thủy
Chọn C
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 19 Mã đề 1881
Gọi
M
l trung điểm của
CD
. Do các tam giác
ACD
và
BCD
l các tam giác đu nên ta có :
()
AM CD
CD ABM
BM CD
⊥
⊥
⊥
(1)
Do
()AB ABM
(2)
Từ (1) và (2) ta có
CD AB⊥
nên góc giữa hai đường thng
AB
và
CD
bằng
0
90
Câu 30. Tìm
m
để hàm số
2
20
()
10
x m khi x
fx
x x khi x
+
=
+ +
liên tục tại
0x =
A.
1
.
4
m =
B.
1.m =
C.
1
.
2
m =
D.
0.m =
Lời giải
Tác giả: Trần Thị Thủy ; Fb: Trần Thủy
Chọn C
Ta có
00
lim ( ) lim( 2 ) 2 ; (0) 1
xx
f x x m m f
−−
→→
= + = =
và
2
00
lim ( ) lim( 1) 1
xx
f x x x
++
→→
= + + =
Để hàm số liên tục tại
0x =
điu kin là:
00
1
lim ( ) lim ( ) (0) 2 1
2
xx
f x f x f m m
−+
→→
= = = =
Chọn đáp án C.
Câu 31 .
(
)
2
lim 3
x
x x x
→+
+−
bằng
A.
+
. B.
3
2
. C.
3
. D.
0
.
Lời giải
Tác giả: Mai Ngc Thi ; Fb: Mai Ngc Thi
Chọn B
(
)
2
lim 3
x
x x x
→+
+−
22
2
3
lim
3
x
xx
x
xx
→+
+−
=
++
2
3
lim
3
x
x
xx
→+
=
++
2
3
lim
3
11
x
x
x
x
→+
=

++


2
3
lim
3
11
x
x
→+
=
++
3
2
=
.
Câu 32. Tìm khng định sai trong các khẳng định sau :
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 20 Mã đề 1881
A.
G
là trọng tâm tam giác
ABC
0GA GB GC + + =
.
B.
I
l trung điểm của
AB
2MA MB MI + =
,
M
.
C.
G
là trọng tâm tam giác
ABC
3MA MB MC MG + + =
,
M
.
D.
. ' ' ' 'ABCD A B C D
là hình hp. Khi đ ta c :
'AB AD AA AC+ + =
.
Lời giải
Tác giả: Mai Ngc Thi ; Fb: Mai Ngc Thi
Chọn D
Ta có
. ' ' ' 'ABCD A B C D
là hình hp nên
ABCD
là hình bình hành nên :
AB AD AC+=
nên
'AB AD AA AC+ + =
là sai.
Câu 33.
2
3
lim( 4)
x
x
→
−
bằng:
A.
2
. B.
1
. C.
4−
. D
1−
.
Lời giải
Tác giả, Fb: Lê Tun Duy
Chọn D
Ta có :
( )
2
2
3
lim( 4) 3 4 1.
x
x
→
− = − = −
Câu 34. Cho lăng trụ tam giác
.ABC A B C
có
' , ,AA a AB b AC c= = =
.Hãy biểu diễn vectơ
BC
theo các vectơ
, , .a b c
A.
B C a b c
= + −
. B.
B C a b c
= − + −
. C.
B C a b c
= − +
D.
B C a b c
= − +
.
Lời giải
Tác giả, Fb: Lê Tun Duy
Chọn C
Ta có :
' AC ' ( A'A)B C AB AC A B

= − = − −
A'A AB AC a b c= − + = − − +
.
Vậy:
B C a b c
= − − +
Câu 35.
( )( )( ) ( )
0
1 1 2 1 3 ... 1 2019 1
lim
x
x x x x
x
→
+ + + + −
bằng
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 21 Mã đề 1881
A.
2018.2019
. B.
1009.2019
. C.
1010.2019
. D.
0
.
Lời giải
Tác giả: Bùi Bài Bình ; Fb: Bui Bai
Chọn C
Đặt
( ) ( )( ) ( )
1 1 2 1 2019 1f x x x x= + + + −
2019 2018 2
2019 2018 2 1
11a x a x a x a x= + + + + + −
2019 2018 2
2019 2018 2 1
a x a x a x a x= + + + +
.
Suy ra
( )
2018 2017
2019 2018 2 1
fx
a x a x a x a
x
= + + + +
.
Với
( )
1
2019 1 2019
1 2 3 2019 1010.2019
2
a
+
= + + + + = =
.
Vậy
( )
( )
2018 2017
2019 2018 2 1 1
00
lim lim 1010.2019
xx
fx
a x a x a x a a
x
→→
= + + + + = =
.
Câu 36. Biết hàm số
( ) ( )
2
2
khi 1
1
,
1
khi 1
2
x ax b
x
x
f x a b R
x
++
−
=
−=
liên tục tại
1x =
. Hãy tính
25S a b=+
A.
10S =
. B.
7S =
. C.
4S =
. D.
2S =
.
Lời giải
Tác giả: Bùi Bài Bình ; Fb: Bui Bai
Chọn C
Điu kin cần: Gi sử hàm số liên tục tại
1x =
.
Suy ra
( )
22
22
11
1
lim 1 lim
1 1 2
xx
x ax b x ax b
f
xx
→→
+ + + +
= = −
−−
.
Suy ra phương trnh
2
0x ax b+ + =
có nghim
1x =
10ab + + =
1ba = − −
.
Ta có:
( )
( )( )
( )( )
2
2
1 1 1 1
11
12
lim lim lim =lim
1 1 1 1 2
x x x x
x x a
x ax b x a a
fx
x x x x
→ → → →
− + +
+ + + + +
= = =
− − + +
.
Mà
( )
1
1
lim
2
x
fx
→
=−
Suy ra
21
3, 2
22
a
ab
+
= − = − =
.
Thử lại:
( )
( )( )
( )( )
( )
2
2
1 1 1 1
12
3 2 2 1
lim lim lim lim 1
1 1 1 1 2
x x x x
xx
x x x
f x f
x x x x
→ → → →
−−
− + −
= = = = − =
− − + +
.
Vậy
3a =−
,
2b =
và
2 5 6 10 4S a b= + = − + =
.
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 22 Mã đề 1881
Câu 37.
2
1
32
lim
1
x
xx
x
→
−+
−
bằng
A.
1−
. B.
2−
C. 2. D. 1.
Lời giải
Tác giả: Quỳnh Thụy Trang; Fb: XuKa
Chọn A
2
1 1 1
3 2 ( 1)( 2)
lim lim lim( 2) 1
11
x x x
x x x x
x
xx
→ → →
− + − −
= = − = −
−−
.
Câu 38. Cho
()fx
liên tục trên
1;5−
thỏa mãn
( 1) 1f −=
,
(5) 6f =
. Phương trnh no sau đây luôn c
nghim trong khong
( 1;5)−
?
A.
( ) 8fx=
. B.
( ) 3fx=
. C.
( ) 5 0fx+=
. D.
( ) 1fx=
.
Lời giải
Tác giả: Quỳnh Thụy Trang ; Fb: XuKa
Chọn B
Gọi
( ) ( )
3g x f x=−
Ta có
( ) ( )
1 1 3 2 0gf− = − − = −
( ) ( )
5 5 3 3 0gf= − =
( ) ( )
1 . 5 0gg −
( )
0gx=
luôn có nghim trong khong
( )
1;5−
( )
3fx=
luôn có nghim trong khong
( )
1;5−
Câu 39. Giá trị của
(
)
2
lim 4 5 1 2n n n+ + −
bằng :
A.
−
. B.
5
2
. C.
+
. D.
5
4
.
Lời giải
Tác giả: Nguyn Thy Linh ; Fb: Nguyn Thy Linh
Chọn D
(
)
(
)
(
)
22
2
22
4 5 1 2 . 4 5 1 2
51
lim 4 5 1 2 lim lim
4 5 1 2 4 5 1 2
n n n n n n
n
n n n
n n n n n n
+ + − + + +
+
+ + − = =
+ + + + + +
2
1
5
5
lim
4
51
42
n
nn
+
==
+ + +
.
Câu 40.
( )
24
lim 5 3 2019
x
xx
→−
−−
bằng
A.
−
. B.
3−
. C.
2019−
. D.
+
.
Lời giải
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 23 Mã đề 1881
Tác giả: Nguyn Thy Linh ; Fb: Nguyn Thy Linh
Chọn A
( )
2 4 4
42
53
lim 5 3 2019 lim 2019
xx
x x x
xx
→− →−


− − = − − =−




.
Câu 41. Cho hình chóp
.S ABCD
c đáy
ABCD
là hình thoi tâm
O
. Biết
,SA SC SB SD==
. Khng
định no sau đây sai?
A.
( )
SO ABCD⊥
B.
( )
AC SBD⊥
C.
( )
BD SAC⊥
D.
( )
AB SAD⊥
Lời giải
Tác giả: Phạm Ngc Hưng; Fb: Hưng Phạm Ngc
Chọn D
Khng định sai là
( )
AB SAD⊥
.
Câu 42. Cho hình chóp
.S ABC
, c đáy
ABC
l tam giác đu cạnh
a
. Gọi
O
l tâm đường tròn ngoại
tiếp tam giác
ABC
. Biết
SO
vuông góc với đáy
( )
ABC
và
2SO a=
. Gọi
M
l điểm thuc
đường cao
AH
của tam giác
ABC
. Xét mặt phng
( )
P
đi qua
M
và vuông góc với
AH
. Đặt
3
,
3
a
AM x x=
. Xác định vị tr điểm
M
để thiết din của hình chóp cắt bởi mặt phng
( )
P
có din tích lớn nht. Khi đ tỷ số
AM
AH
bằng
A.
4
5
AM
AH
=
B.
5
6
AM
AH
=
C.
3
4
AM
AH
=
D.
2
3
AM
AH
=
Lời giải
Tác giả: Phạm Ngc Hưng; Fb: Hưng Phạm Ngc
Chọn C
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 24 Mã đề 1881
Trong mặt phng
( )
ABC
kẻ đường thng qua
M
và song song với
BC
cắt
,AB AC
lần lượt
tại
,EF
. Trong mặt phng
( )
SAH
kể đường thng qua
M
và song song với
SO
, cắt
SH
tại
I
. Trong mặt phng
( )
SBC
kẻ đường thng đi qua
I
và song song với
BC
cắt
,SC SB
lần
lượt tại
,PQ
. Khi đ thiết din cần tìm là hình thang
EFPQ
.
Ta có
2
2 2 2
39
4
33
aa
SA SB SC SO AO a= = = + = + =
,
2
2
3 7 3
4
66
aa
SH a

= + =



.
3
. 4 3
2
MI MH SO a
MI MH x
SO HO HO

= = = −



.
23
.
3
EF AM BC x
EF AM
BC AH AH
= = =
.
73
7
2
HI MH SH a
HI MH x
SH HO HO

= = = −



.
3
. 2 3
3
PQ SI BC a
PQ SI x
BC SH SH

= = = −



.
Do đ
( )
( )( )
2
4 3 3 6 4 3
.
3
2 3 4
EFPQ
x a a x
PQ EF MI
a
S
−−
+
= =
.
2
3
maxS
4
EFPQ
a
=
khi
33
4 3 3 6 4 3
8
a
x a a x x− = − =
.
Vậy
33
3
8
4
3
2
a
AM
AH
a
==
.
Q
P
F
E
O
B
A
C
S
H
M
I
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 25 Mã đề 1881
Câu 43. [Mc đ 2]
0
5 3 3
lim
x
xa
x
bc
→
+−
=
(với
,,abc
). Tnh
a b c−+
.
A. 0. B. 6. C. 8. D. 4.
Lời giải
Tác giả: Phạm Chí Dũng ; Fb: Phạm Chí Dũng
Chọn B
Ta c:
0
5 3 3
lim
x
x
x
→
+−
( )
0
5 3 3
lim
5 3 3
x
x
xx
→
+−
=
++
0
5
lim
5 3 3
x
x
→
=
++
5
23
=
.
Vậy
5a =
,
2b =
,
3c =
. Suy ra:
6a b c− + =
.
Câu 44. [Mc đ 2]
( )
3
lim 2018 2 5
x
xx
→−
− + +
bằng
A.
+
. B. 0. C.
−
. D.
2018−
.
Lời giải
Tác giả: Phạm Chí Dũng ; Fb: Phạm Chí Dũng
Chọn D
Ta c:
( )
3
lim 2018 2 5
x
xx
→−
− + +
3
23
25
lim 2018
x
x
xx
→−

= − + +


.
M
3
lim
x
x
→−
= −
;
23
25
lim 2018 2018
x
xx
→−

− + + = −


.
Vậy
( )
3
lim 2018 2 5
x
xx
→−
− + + = +
.
Câu 45. Hàm số
( )
2
43
2
−+
=
−
xx
fx
x
.không liên tục tại
A.
3=x
. B.
2=x
. C.
1=x
. D.
0=x
.
Lời giải
Tác giả: Diệp Tuân; Fb: Tuân Diệp
Chọn B
Hàm số
( )
fx
c xác định
\2D =
.
Do
2xD=
nên hàm số
( )
fx
không liên tục tại
2=x
.
Câu 46.
13
lim
25
→−
−
+
x
x
x
.bằng
A.
3
2
−
. B.
1
5
. C.
1
2
. D.
3
5
−
.
Lời giải
Tác giả: Diệp Tuân; Fb: Tuân diệp
Chọn B
Ta có
1
3
1 3 3
lim lim .
5
2 5 2
2
→− →−
−
−
= = −
+
+
xx
x
x
x
x
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 26 Mã đề 1881
Câu 47. Giá trị của
2
23
lim
32
n
nn
+
−+
bằng:
A.
1
. B.
2
3
. C.
+
. D.
0
.
Lời giải
Tác giả: Hà Lê; Fb: Ha Le
Chọn D
2
2
2
23
2 3 0
lim lim 0
12
3 2 3
3
n
nn
nn
nn
+
+
= = =
−+
−+
.
Câu 48. Cho hai đường thng phân bit
a
,
b
v điểm
O
không thuc mặt phng
( )
P
. Mnh đ nào
sau đây l sai ?
A. Nếu hai đường thng
a
và
b
cùng vuông góc với mặt phng
( )
P
thì chúng song song với
nhau.
B. Nếu
//ab
và
a
vuông góc với mặt phng
( )
P
thì
b
cũng vuông gc với mặt phng
( )
P
.
C. Có duy nht mt đường thng
d
đi qua điểm
O
và song song với mặt phng
( )
P
.
D. Có duy nht mt đường thng
d
đi qua điểm
O
và vuông góc với mặt phng
( )
P
.
Lời giải
Tác giả: Hà Lê; Fb: Ha Le
Chọn C
Mnh đ
A
,
B
,
D
đng (theo các tnh cht đã biết).
Mnh đ
C
sai vì qua mt điểm nằm ngoài mt mặt phng có vô số đường thng song song với
mặt phng đ.
Câu 49.
2
10 30
lim
5.30 4.20
nn
nn
+
+
−
bằng
A.
+
. B.
−
. C.
900
. D.
180
.
Lời giải
Tác giả: Đặng Ân ; Fb:Đặng Ân
Chọn D
2
10 30
lim
5.30 4.20
nn
nn
+
+
−
10 900.30
lim
5.30 4.20
nn
nn
+
=
−
1
900
3
lim
2
5 4.
3
n
n

+


=

−


180=
.
Câu 50. Cho hình chóp
.S ABCD
c đáy
ABCD
là hình vuông cạnh
a
,
2SA a=
và
SA
vuông góc
với mặt phng đáy
( )
ABCD
. Gọi
là góc giữa
SB
và mặt phng
( )
SAC
. Tính
tan
.
A.
1
tan
5
=
. B.
1
tan
3
=
. C.
tan 2
=
. D.
1
tan
2
=
.
Lời giải
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC Trang 27 Mã đề 1881
Tác giả: Đặng Ân ; Fb:Đặng Ân
Chọn A
Gọi
O
l giao điểm hai đường chéo của hình vuông
ABCD
.
( )
BO AC
BO SAC
BO SA
⊥
⊥
⊥
SO
là hình chiếu của
SB
lên mặt phng
( )
SAC
( )
;SB SO
=
BSO=
(do tam giác
SBO
vuông tại
O
nên
BSO
là góc nhọn).
Xét tam giác
SBO
có
tan
BO
BSO
SO
=
22
BO
SA AO
=
+
2
2
2
2
2
2
a
a
a
=
+
1
5
=
.
| 1/32
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
GIẢI CHI TIẾT ĐỀ GIỮA HỌC KỲ II
MÔN TOÁN – KHỐI 11 - 2018 - 2019
TRƯỜNG THPT VIỆT NAM - BA LAN x − 3  khi x  3
Câu 1. Tìm m để hàm số f ( x) =  x +1 − 2
liên tục trên tập xác định.  m khi x = 3  A. m = 2 . B. m = 4 . C. m = 0 . D. m = 1. 2 3 n Câu 2.
Tính tổng: S = 0,3 + (0,3) + (0,3) +...+ (0,3) +... 3 5 11 7 A. . B. . C. . D. . 7 7 7 3 Câu 3. Cho phương trình 5 4 2
x − 7x + 3x + 2 = 0 . Mệnh đề nào sau đây là đúng ?
A. Phương trình không có nghiệm thuộc khoảng (0; 2) .
B. Phương trình có ít nhất hai nghiệm thuộc khoảng ( 1 − ;3) .
C. Phương trình không có nghiệm thuộc khoảng (−1; ) 1 .
D. Phương trình có đúng một nghiệm thuộc khoảng (−1; 2) . Câu 4.
Tìm khẳng định đúng: A. 4 lim x = − . B. 3 lim x = + . C. lim x q = 0 , (q  ) 1 .
D. lim x = x0 . x→− x→− x→+ x→x0 3x + a Câu 5. Biết lim
= −  thì giá trị của a thỏa mãn + x 1 →− x +1 A. a  3 − . B. a  3 − . C. a  3 . D. a  5 . 2 8n +1 + 4 − 3n Câu 6. Cho lim
= a 2 + b . Mệnh đề đúng là n + 3
A. a = 3b .
B. a + b + 3  3 .
C. 2a + b = 3 .
D. a + b  2 . Câu 7.
Tìm hệ thức liên hệ giữa các số thực a, b để ( 2 2 lim
n + an + 3 − n + bn −1) =1.
A. a + b = 2 .
B. a + b = 1.
C. a − b = 2 .
D. a − b = 1. Câu 8.
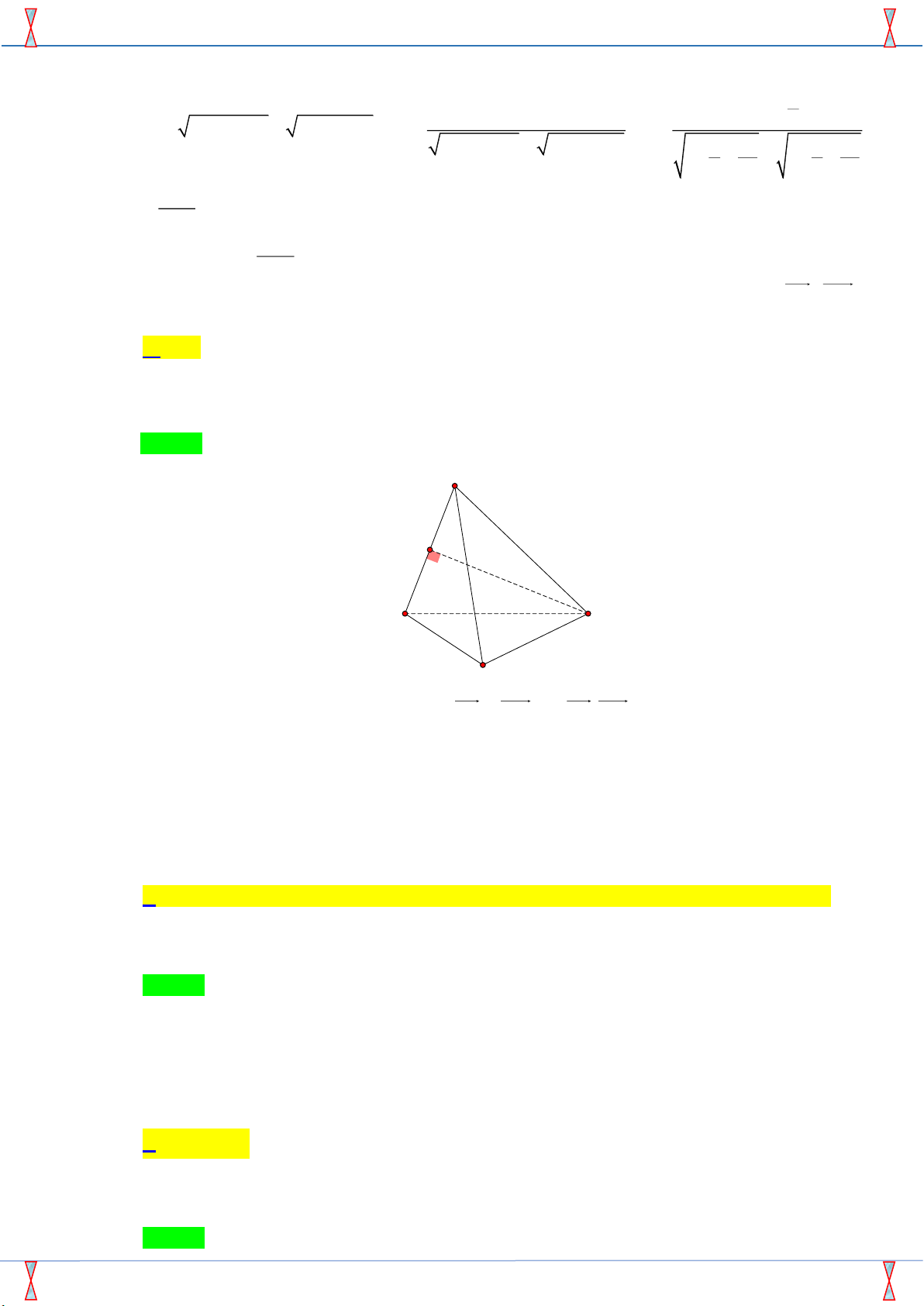
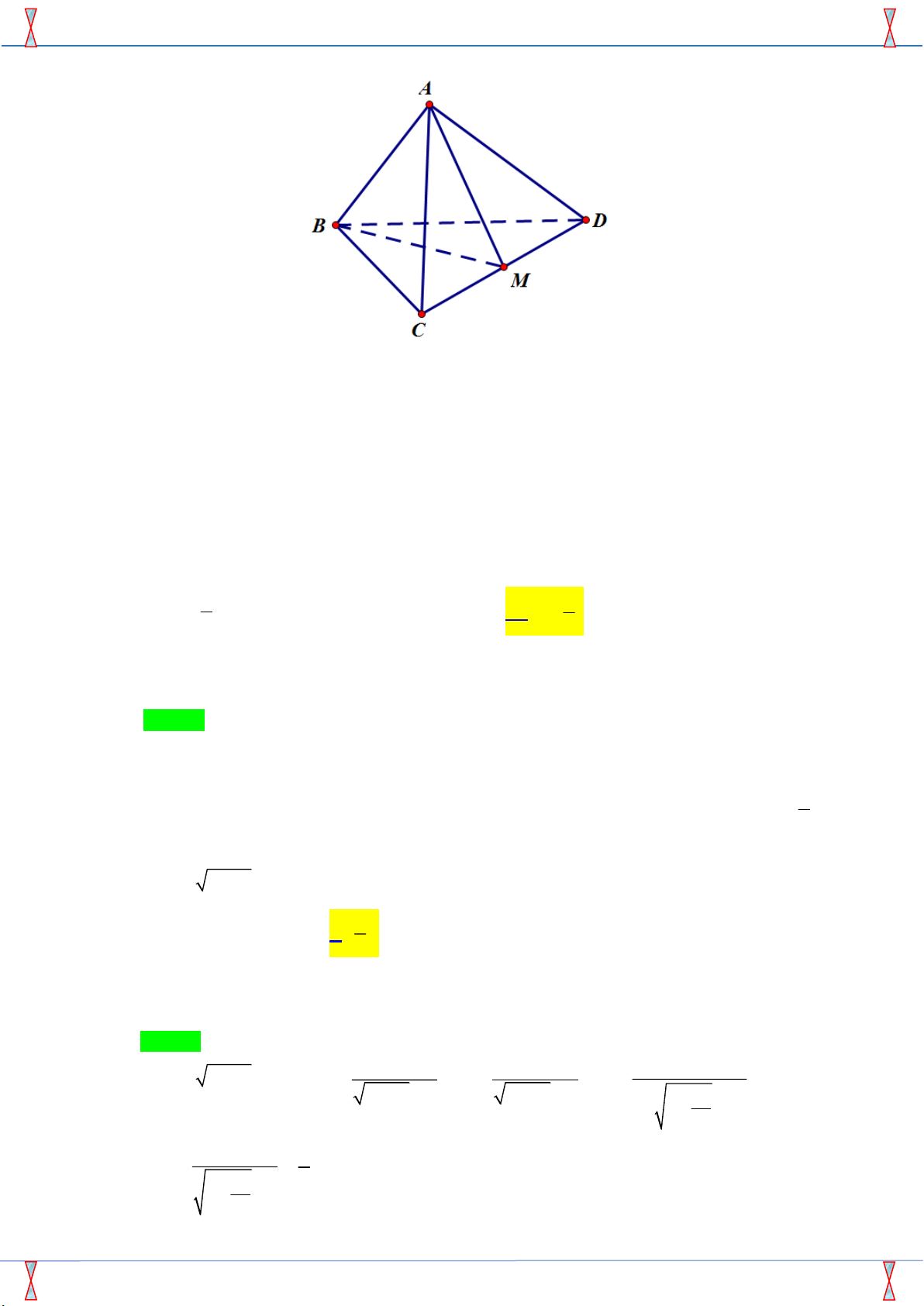
Cho tứ diện đều ABCD, M là trung điểm của cạnh AB . Khi đó góc giữa hai vectơ A , B CM bằng: A. 90 . B. 45 . C. 120 . D. 60 . Câu 9.
Chọn mệnh đề đúng trong các mệnh đề sau: Trong không gian
A. Ba véctơ đồng phẳng khi và chỉ khi ba véc tơ phải nằm trong cùng một mặt phẳng.
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 1 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
B. Ba véctơ đồng phẳng khi và chỉ khi giá của ba véctơ đó song song với nhau .
C. Ba véctơ đồng phẳng khi và chỉ khi ba véctơ cùng hướng.
D. Ba véctơ đồng phẳng khi và chỉ khi giá của ba véctơ cùng song song với một mặt phẳng
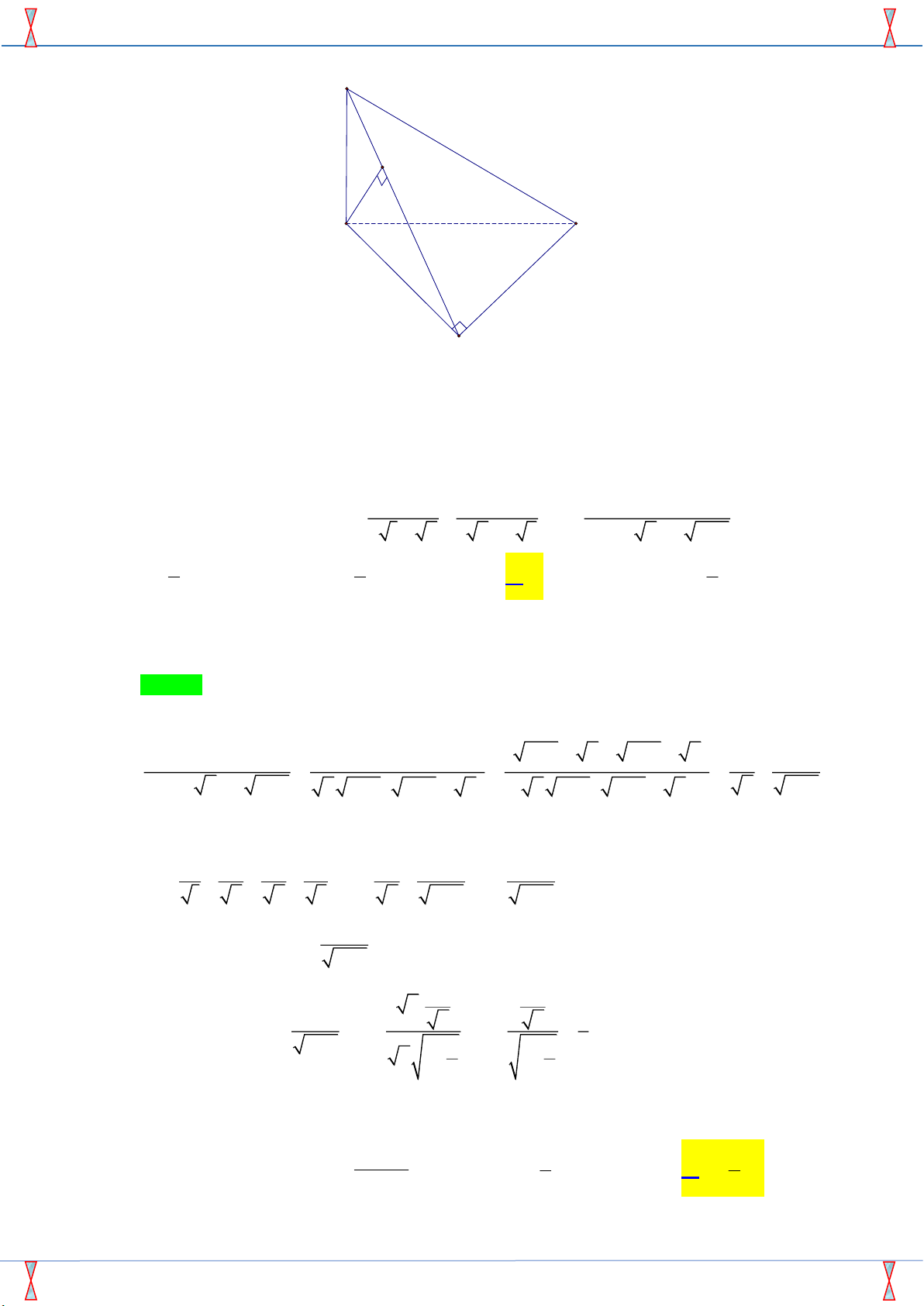
Câu 10. Cho hình chóp S.ABC có SA ⊥ ( ABC ) và AB ⊥ BC . Gọi H là hình chiếu vuông góc của A
lên SB khẳng định nào sau đây là đúng?
A. AH ⊥ SC .
B. AH ⊥ AC .
C. AH ⊥ AB .
D. AH ⊥ ( SAC ) . 1 1 1
Câu 11. Tính giới hạn của dãy số u = + +...+ n 2 1 + 2 3 2 + 2 3 (n+ ) 1 n + n n +1 4 2 3 A. . B. . C. 1. D. . 5 3 2
Câu 12. Dãy số nào sau đây có giới hạn bằng 0 ? 2 n n n − 3n  6   2  A. 2 n − 4n . B.   . D. −   . n + . C. 1  5   3 
Câu 13. Cho các khẳng định:
(I) Cho hàm số y = f ( x) liên tục trên a;b và f (a). f (b)  0 . Khi đó phương trình
f ( x) = 0 có ít nhất một nghiệm trên khoảng ( ; a b) .
(II) Cho hàm số y = f ( x) liên tục trên a;b và f (a). f (b)  0 . Khi đó phương trình
f ( x) = 0 không có nghiệm trên khoảng ( ; a b) .
Trong các khẳng định trên: A. Chỉ (I) đúng.
B. Cả (I), (II) đúng. C. Cả (I), (II) sai. D. Chỉ (II) đúng.
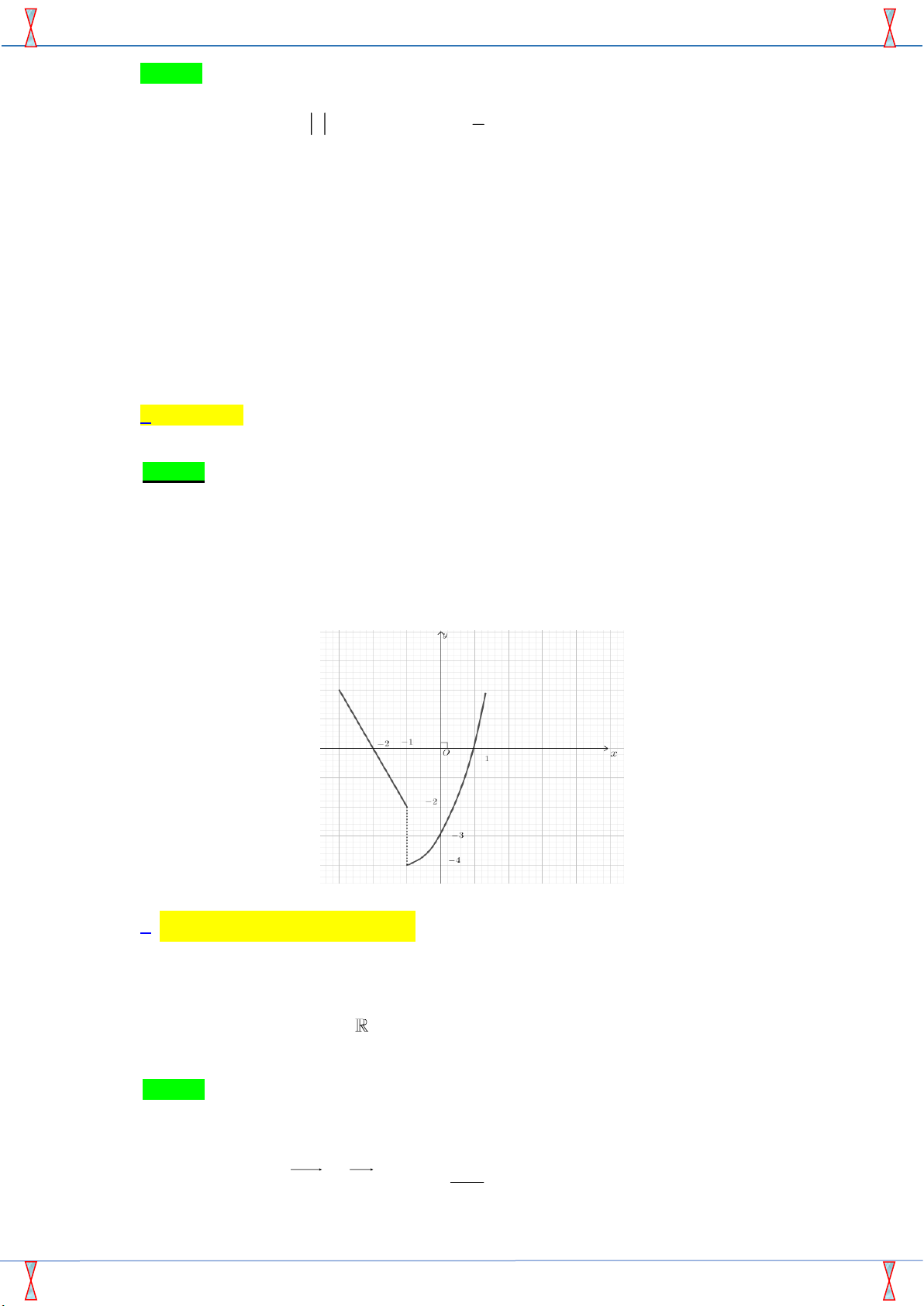
Câu 14. Cho hàm số f ( x) có đồ thị như hình vẽ Chọn đáp án đúng
A. Hàm số f ( x) gián đoạn tại x = 1 − .
B. Hàm số f ( x) liên tục tại x = 1 − .
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 2 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
C. Hàm số f ( x) liên tục trên khoảng (−3; ) 1 .
D. Hàm số f ( x) liên tục trên .
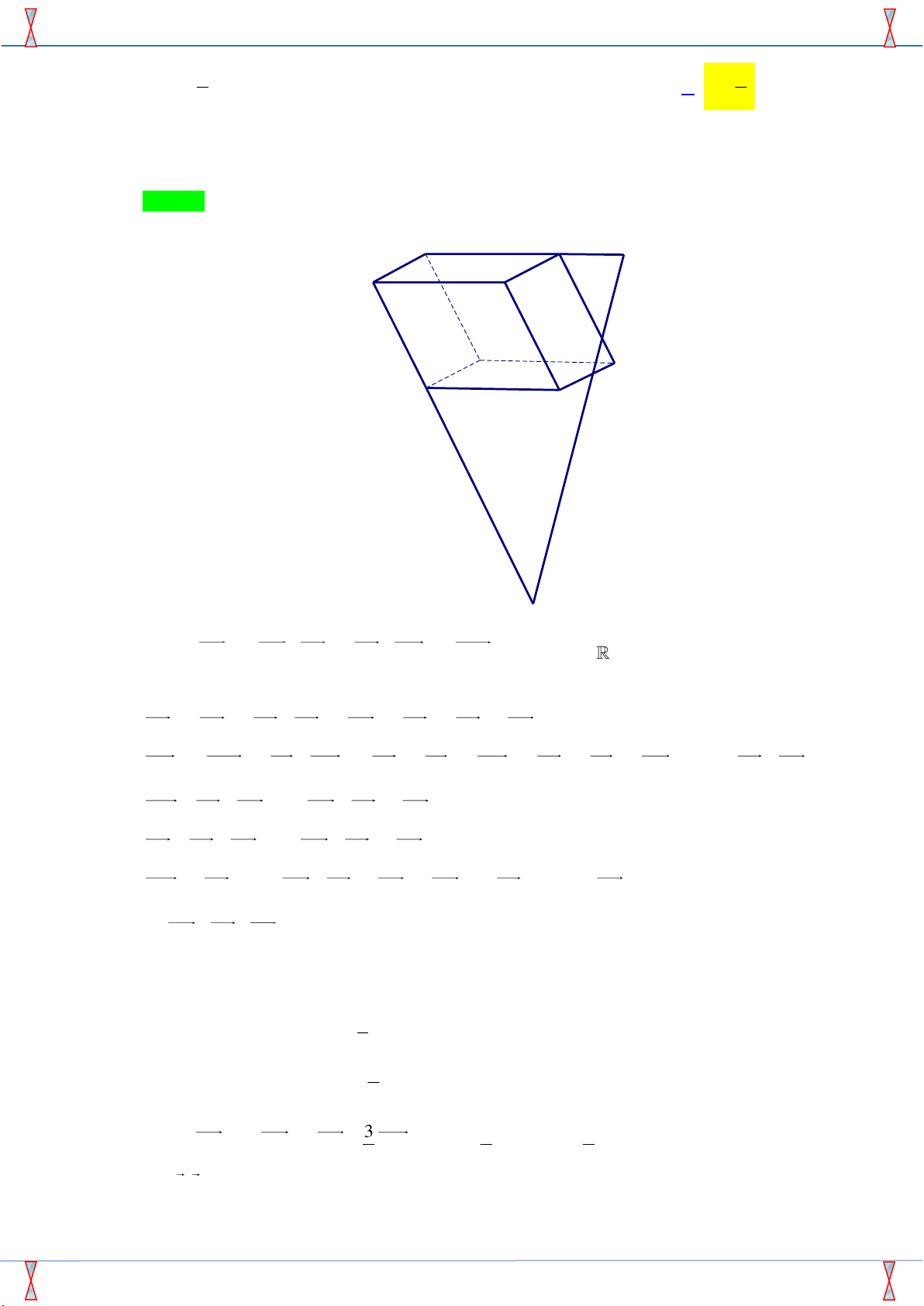
Câu 15. TCho hình hộp ABC . D A BCD
  . Một đường thẳng  cắt các đường thẳng AA , BC,C D   lần lượ MA
t tại M , N , P sao cho NM = 3NP . Tính k = MA . 2 2 A. k = . B. k = 2 . C. k = 3. D. k = . 3 3
Câu 16. Cho u, v bất kì, chọn mệnh đề đúng? u v u v A. (u v) . cos , = . B. .
u v = u . v .cos (u,v) . C. . u v = .
u v .cos (u,v).D. (u v) . cos , = . . u v u . v Câu 17. ( 2018 2019 lim 4 − n − n ) bằng A. 0 . B. − . C. 2019 − . D. + .
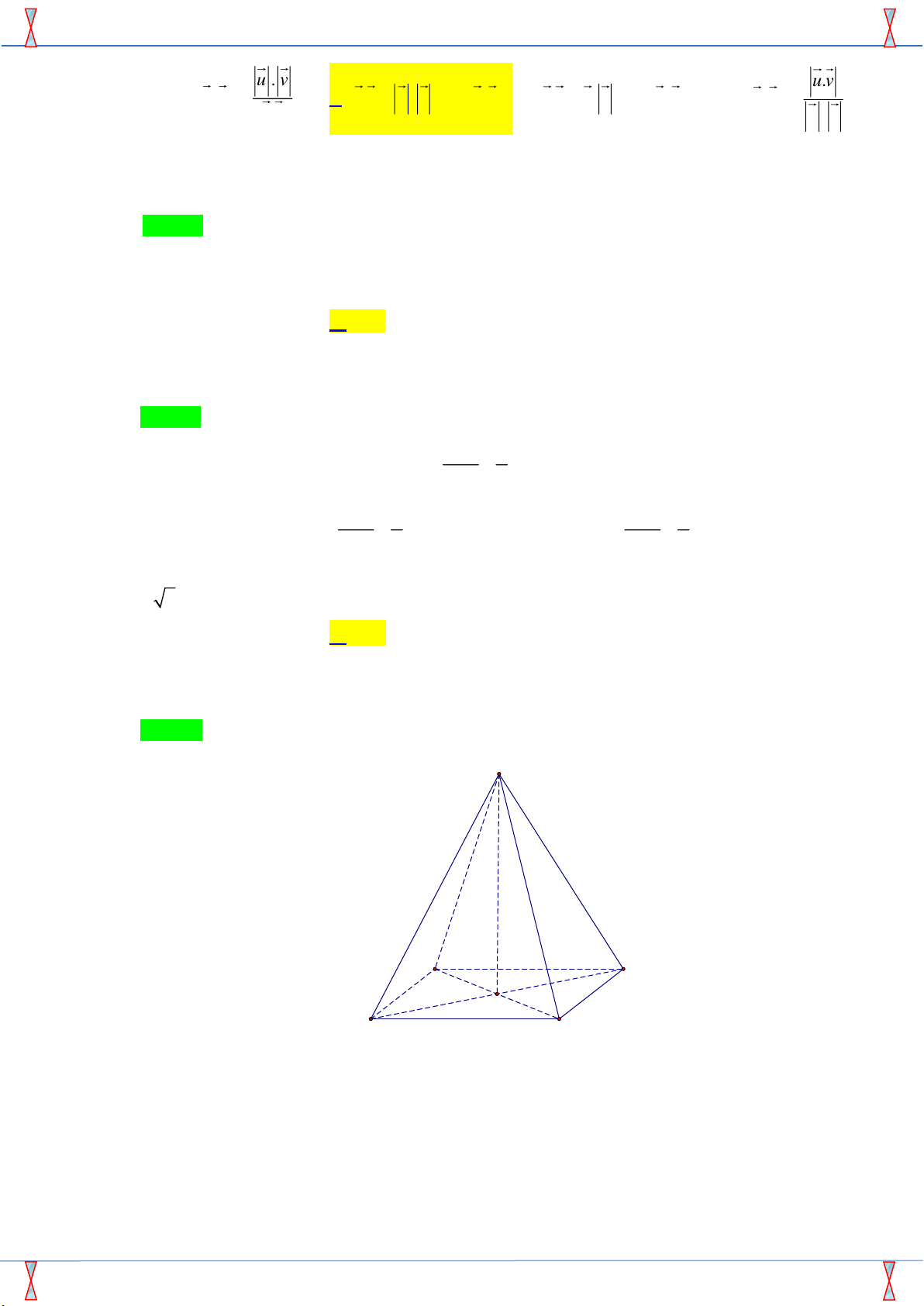
Câu 18. Cho hình chóp tứ giác S.ABCD , có đáy ABCD là hình vuông cạnh a , các cạnh bên đều bằng
a 2 . Góc giữa cạnh bên SB và mặt phẳng ( ABCD) bằng A. 0 30 . B. 0 60 . C. 0 90 . D. 0 45 . Câu 19. Rút gọn 2 4 6 2 = 1+ sin + sin + sin + ...+ sin n S x x x
x + ... với sin x  1  . 1 A. 2 S = cos x . B. 2 S = tan x . C. S = S = + x . 2 1+ . D. 2 1 tan sin x   a
Câu 20. lim  x + 3x + 5x + 7x + ... 2019x − x  =
(với a , b nguyên dương nhỏ nhất). Tính x→+   b   a + b . A. 6 . B. 5 . C. 3 . D. 4 . 2  x − 3x + 2  khi x  2
Câu 21. Tìm a để hàm số f (x) =  x − 2 liên tục trên R.
 ax + a −5 khi x  2 A. 1. B. 3. C. 0. D. 2.  x +1 −1  khi x  0  x
Câu 22. Cho hàm số f (x) = 
. Chọn khẳng định đúng? 1  khi x = 0  2
A. Hàm số gián đoạn tại x = 0 .
B. Hàm số liên tục trên R.
C. Hàm số liên tục trên  1 − ;+).
D. Hàm số liên tục trên (−3, 2) .
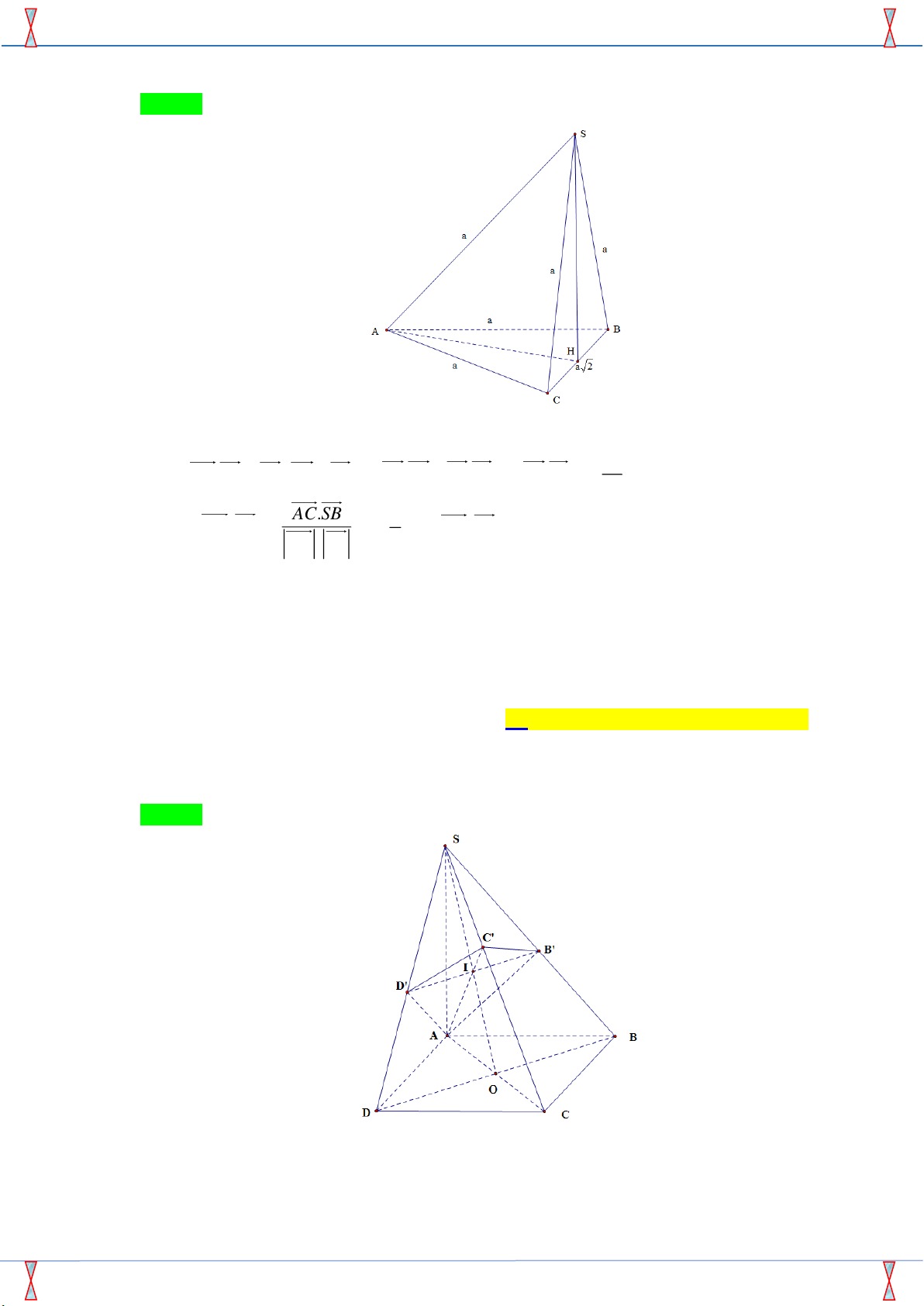
Câu 23. Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a 2 và BC = 2a . Khi đó góc giữa hai
đường thẳng AC và SB bằng
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 3 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 A. 30 . B. 90 . C. 45 . D. 60 .
Câu 24. Cho hình chóp S.ABCD có đáy là hình vuông ABCD và SA vuông góc với mặt phẳng đáy
( ABCD) . Một mặt phẳng ( ) đi qua A và vuông góc với SC cắt hình chóp theo thiết diện là:
A. hình thoi có một góc có số đo bằng 60 . B. hình vuông. C. hình bình hành.
D. tứ giác có hai đường chéo vuông góc.
Câu 25. Cho tứ diện ABCD . Gọi M , N ,G lần lượt là trung điểm của AB, CD, MN . Chọn khẳng định đúng: 1
A. GA + GB + GC + GD = 2MN . B. MN = (AD+CB). 2 1 1 C. MN = (AC +BD). D. MN = (AB+CD) 2 2
3 5x + 3 − x + 3 5 1 Câu 26. lim = − ( với ,
m n là các số nguyên dương). Tính m − n ? 2 x 1 → x −1 m n A. 15. B. 14. C. 12. D. 16.
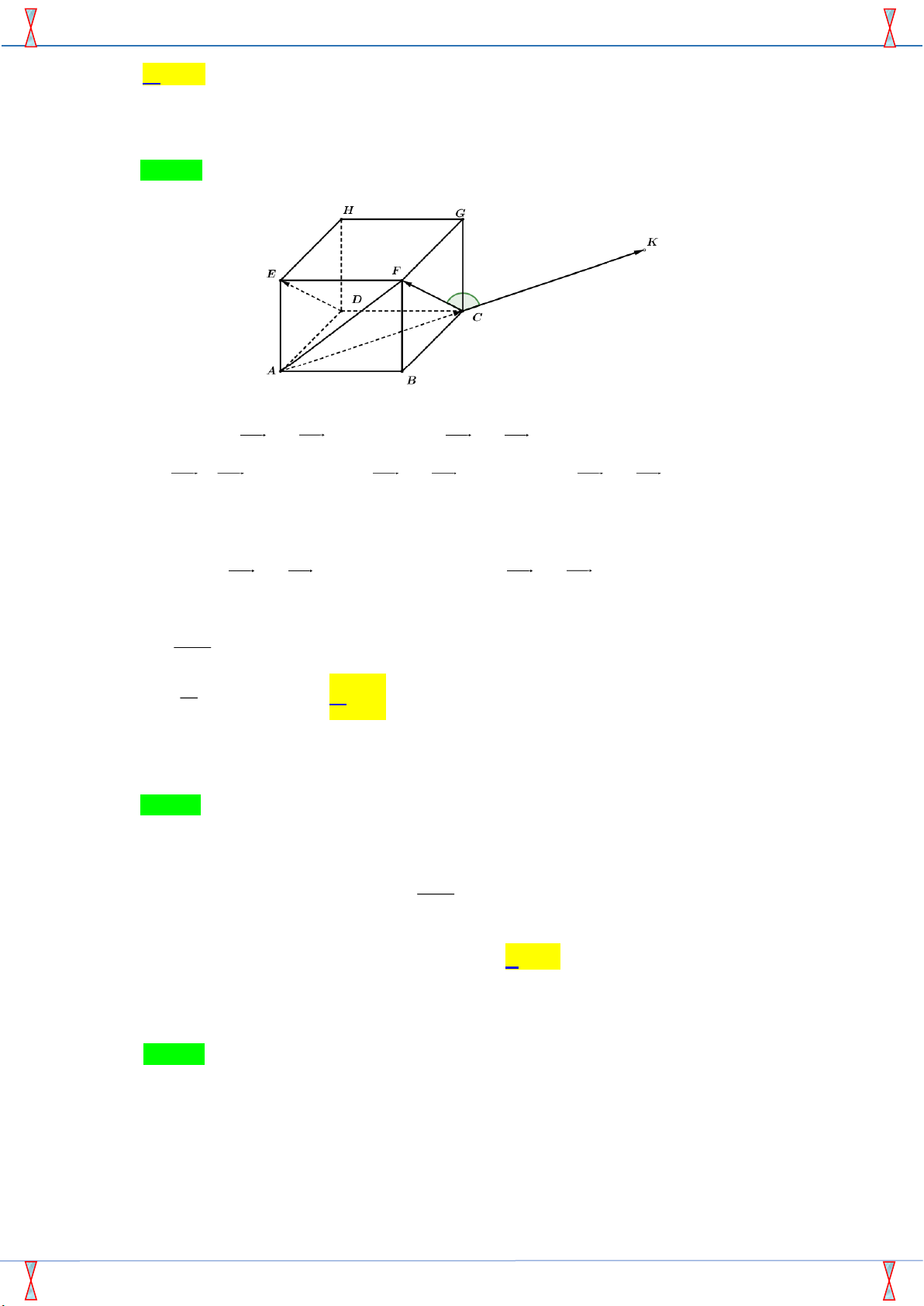
Câu 27. Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp véctơ AC và DE ? A. 120 . B. 45 . C. 60 . D. 90 . x + 5 Câu 28. lim bằng − x 3 → x − 3 15 A. − . B. − . C. 1. D. + . 2
Câu 29. Cho tứ diện đều ABCD cạnh a . Góc giữa AB và CD bằng: A. 0 60 . B. 0 30 . C. 0 90 . D. 0 45 . x + 2m khi x  0
Câu 30. Tìm m để hàm số f (x) =  liên tục tại x = 0 2
x + x +1 khi x  0 1 1 A. m = . B. m = 1. C. m = . D. m = 0. 4 2 Câu 31. x + − bằng →+ ( 2 lim x 3 x x ) 3 A. + . B. . C. 3 . D. 0 . 2
Câu 32. Tìm khẳng định sai trong các khẳng định sau :
A. G là trọng tâm tam giác ABC GA + GB + GC = 0 .
B. I là trung điểm của AB MA + MB = 2MI , M  .
C. G là trọng tâm tam giác ABC MA + MB + MC = 3MG , M  . D. ABC . D '
A B' C' D' là hình hộp. Khi đó ta có : AB + AD + A ' A = AC . Câu 33. 2 lim (x − 4) bằng: x→ 3
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 4 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 A. 2 . B. 1. C. 4 − . D −1.
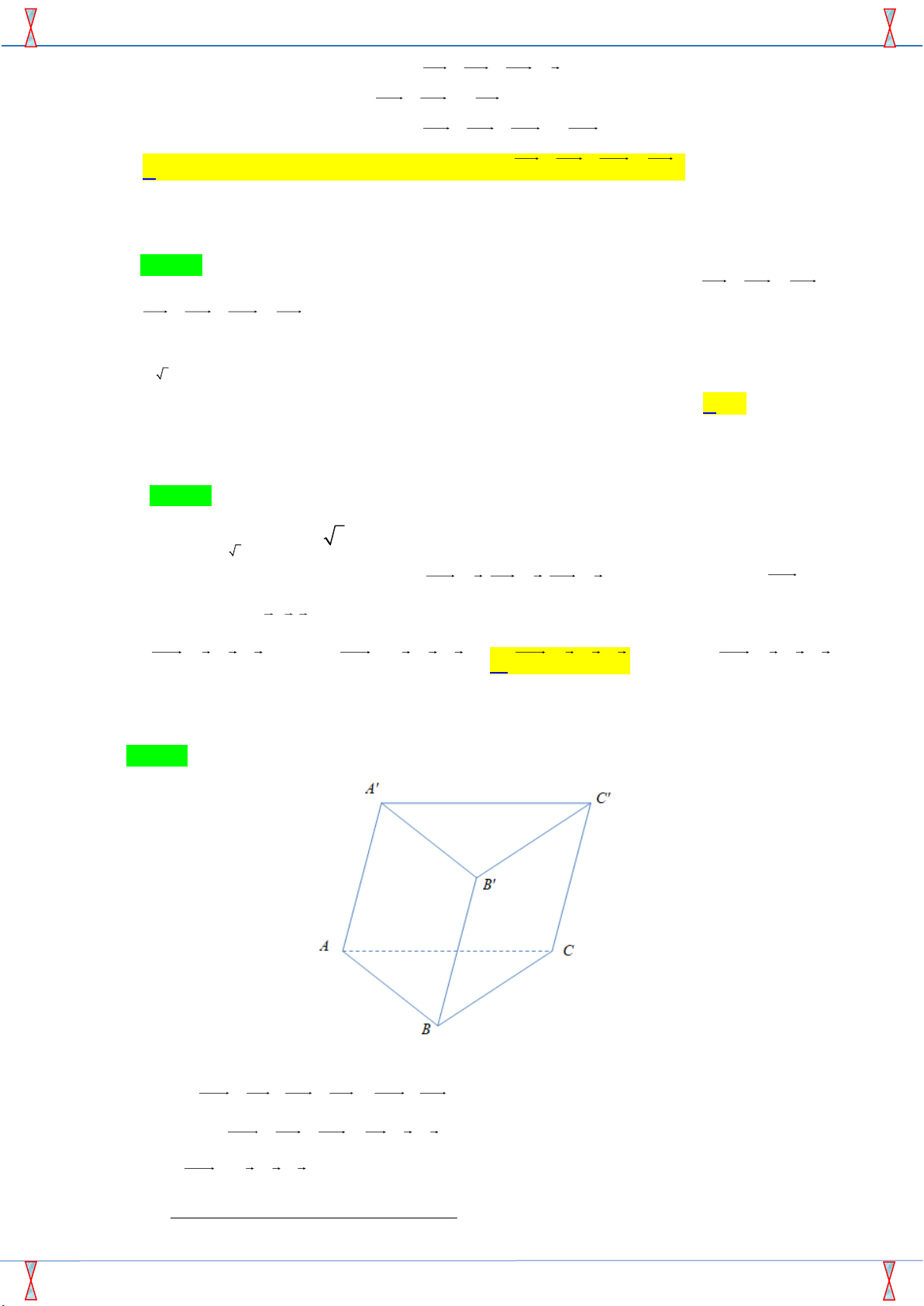
Câu 34. Cho lăng trụ tam giác AB . C A BC  có AA' = , a AB = ,
b AC = c .Hãy biểu diễn vectơ B C  theo các vectơ , a , b . c A. B C
 = a + b − c B. B C
 = −a + b − c . C. B C
 = a − b + c D. B C
 = a − b + c .
(1+ x)(1+ 2x)(1+3x)...(1+ 2019x)−1 Câu 35. lim bằng x→0 x A. 2018.2019 . B. 1009.2019 . C. 1010.2019 . D. 0 . 2
x + ax + b khi x 1  2  −
Câu 36. Biết hàm số f ( x) x 1 = 
(a,bR) liên tục tại x =1. Hãy tính S = 2a + 5b 1 − khi x =1  2 A. S = 10 . B. S = 7 . C. S = 4 . D. S = 2 . 2 x − 3x + 2 Câu 37. lim bằng x 1 → x −1 A. −1. B. 2 − C. 2. D. 1.
Câu 38. Cho f (x) liên tục trên −1;5 thỏa mãn f ( 1
− ) =1, f (5) = 6 . Phương trình nào sau đây luôn có
nghiệm trong khoảng (−1;5) ?
A. f (x) = 8 .
B. f (x) = 3 .
C. f (x) + 5 = 0 .
D. f (x) = 1 . Câu 39. Giá trị của ( 2 lim
4n + 5n +1 − 2n) bằng : 5 5 A. − . B. . C. + . D. . 2 4 Câu 40. ( 2 4
lim 5 − 3x − 2019x ) bằng x →− A. − . B. − 3 . C. − 2019 . D. + .
Câu 41. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O . Biết SA = SC, SB = SD . Khẳng
định nào sau đây sai?
A. SO ⊥ ( ABCD)
B. AC ⊥ ( SBD) C. BD ⊥ (SAC )
D. AB ⊥ (SAD)
Câu 42. Cho hình chóp S.ABC , có đáy ABC là tam giác đều cạnh a . Gọi O là tâm đường tròn ngoại
tiếp tam giác ABC . Biết SO vuông góc với đáy ( ABC ) và SO = 2a . Gọi M là điểm thuộc
đường cao AH của tam giác ABC . Xét mặt phẳng (P) đi qua M và vuông góc với AH . Đặt a 3
AM = x, x
. Xác định vị trí điểm M để thiết diện của hình chóp cắt bởi mặt phẳng (P) 3 AM
có diện tích lớn nhất. Khi đó tỷ số bằng AH
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 5 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 AM 4 AM 5 AM 3 AM 2 A. = B. = C. = D. = AH 5 AH 6 AH 4 AH 3 5x + 3 − 3 a
Câu 43. [Mức độ 2] lim =
(với a, b, c
). Tính a − b + c . x→0 x b c A. 0. B. 6. C. 8. D. 4. Câu 44. ( 3 lim 2
− 018x + 2x + 5) bằng x→− A. + . B. 0. C. − . D. 2018 − . x − x +
Câu 45. Hàm số f ( x) 2 4 3 = .không liên tục tại x − 2 A. x = 3 . B. x = 2 . C. x = 1 . D. x = 0 . 1− 3x Câu 46. lim .bằng
x→− 2x + 5 3 1 1 3 A. − . B. . C. . D. − . 2 5 2 5 2 + 3n
Câu 47. Giá trị của lim 2
3n − n + bằng: 2 2 A. 1. B. . C. + . D. 0 . 3
Câu 48. Cho hai đường thẳng phân biệt a , b và điểm O không thuộc mặt phẳng ( P) . Mệnh đề nào sau đây là sai ?
A. Nếu hai đường thẳng a và b cùng vuông góc với mặt phẳng ( P) thì chúng song song với nhau.
B. Nếu a / / b và a vuông góc với mặt phẳng ( P) thì b cũng vuông góc với mặt phẳng ( P) .
C. Có duy nhất một đường thẳng d đi qua điểm O và song song với mặt phẳng ( P) .
D. Có duy nhất một đường thẳng d đi qua điểm O và vuông góc với mặt phẳng ( P) . n n+2 10 + 30 Câu 49. lim bằng 5.30n − 4.20n A. + . B. − . C. 900 . D. 180 .
Câu 50. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA = a 2 và SA vuông góc
với mặt phẳng đáy ( ABCD) . Gọi  là góc giữa SB và mặt phẳng ( SAC ) . Tính tan . 1 1 1 A. tan  = . B. tan  = . C. tan = 2 . D. tan = . 5 3 2
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 6 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
GIẢI CHI TIẾT ĐỀ GIỮA HỌC KỲ II
MÔN TOÁN – KHỐI 11 - 2018 - 2019
TRƯỜNG THPT VIỆT NAM - BA LAN x − 3  khi x  3 Câu 1.
Tìm m để hàm số f ( x) =  x +1 − 2
liên tục trên tập xác định.  m khi x = 3  A. m = 2 . B. m = 4 . C. m = 0 . D. m = 1. Lời giải Chọn B
Tác giả: Trần Công Diêu; Fb: Trần Công Diêu − + + x − (x 3)( x 1 2 3 )
Ta có: lim f ( x) = lim = lim
= 4 và f (3) = m . x→3 x→3 x→3 x +1 − 2 (x −3)
Để hàm số liên tục trên tập xác định thì lim f (x) = f (3)  m = 4 . x 3 → 2 3 n Câu 2.
Tính tổng: S = 0,3 + (0,3) + (0,3) +...+ (0,3) +... 3 5 11 7 A. . B. . C. . D. . 7 7 7 3 Lời giải Chọn A
Tác giả: Trần Công Diêu; Fb: Trần Công Diêu 2 3 n
Ta có dãy số (0,3);(0,3) ;(0,3) ;...;(0,3) ;... là dãy cấp số nhân lùi vô hạn với số hạng đầu
tiên là u = 0,3 và công bội q = 0, 3 1 u 0,3 3 1  S = = = . 1− q 1− 0,3 7 Câu 3. Cho phương trình 5 4 2
x − 7x + 3x + 2 = 0 . Mệnh đề nào sau đây là đúng ?
A. Phương trình không có nghiệm thuộc khoảng (0; 2) .
B. Phương trình có ít nhất hai nghiệm thuộc khoảng ( 1 − ;3) .
C. Phương trình không có nghiệm thuộc khoảng (−1; ) 1 .
D. Phương trình có đúng một nghiệm thuộc khoảng (−1; 2) . Lời giải
Tác giả:Nguyễn Anh Tuấn ; Fb:Nguyễn Ngọc Minh Châu Chọn B
Xét hàm số f ( x) 5 4 2
= x − 7x + 3x + 2 liên tục trên . Ta có: f (− )
1 = −3 ; f (0) = 2 ; f ( ) 1 = −1  f (− )
1 . f (0)  0 và f (0). f ( ) 1  0 . Do đó phương trình 5 4 2
x − 7x + 3x + 2 = 0 có ít nhất một nghiệm thuộc khoảng (−1;0) và ít nhất một
nghiệm thuộc khoảng (0; )
1 nên phương trình có ít nhất hai nghiệm thuộc khoảng ( 1 − ;3) .
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 7 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 Câu 4.
Tìm khẳng định đúng: A. 4 lim x = − . B. 3 lim x = + . C. lim x q = 0 , (q  ) 1 .
D. lim x = x . 0 x→− x→− x→+ x→x0 Lời giải
Tác giả:Nguyễn Anh Tuấn ; Fb:Nguyễn Ngọc Minh Châu Chọn D A sai vì 4
lim x = + ; B sai vì 3
lim x = − ; C sai vì lim x
q  1 khi q  1 và D đúng. x→− x→− x→+ 3x + a Câu 5 . Biết lim
= −  thì giá trị của a thỏa mãn + x 1 →− x +1 A. a  3 − . B. a  3 − . C. a  3 . D. a  5 . Lời giải
Tác giả: Nguyễn Tuyết Lê ; Fb: Nguyen Tuyet Le Chọn C
Ta có lim (3x + a) = 3
− + a ; lim (x + )
1 = 0 ; x +1  0 với x   1 − . + + x 1 →− x 1 →− 3x + a Lại do lim = −  nên 3
− + a  0  a  3 . + x 1 →− x +1 2 8n +1 + 4 − 3n Câu 6. Cho lim = a 2 + b n + . Mệnh đề đúng là 3
A. a = 3b .
B. a + b + 3  3 .
C. 2a + b = 3 .
D. a + b  2 . Lời giải
Tác giả: Nguyễn Tuyết Lê ; Fb: Nguyen Tuyet Le Chọn B  1 4  n  8 + + − 3 1 4 + + − 2 2 8 3 8n +1 + 4 − 3n n n   2 n n Ta có lim = lim = lim = 2 2 − 3. n + 3  3  3 n 1+   1+  n n
Do đó a = 2 ; b = 3 − . Đáp án A, C, D sai. Câu 7.
Tìm hệ thức liên hệ giữa các số thực a, b để ( 2 2 lim
n + an + 3 − n + bn −1) =1.
A. a + b = 2 .
B. a + b = 1.
C. a − b = 2 .
D. a − b = 1. Lời giải
Tác giả:Nguyễn Thành Đô ; Fb: Thành Đô Nguyễn Chọn C
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 8 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 Xét 4 a − b + a − b n + lim ( 4 2 2 + + 3 − + −1) ( ) = lim = lim n n an n bn 2 2
n + an + 3 + n + bn −1 a 3 b 1 1+ + + 1+ − 2 2 n n n n a − b = . 2 a − b Theo giả thiết:
=1  a − b = 2. 2 Câu 8.
Cho tứ diện đều ABCD, M là trung điểm của cạnh AB . Khi đó góc giữa hai vectơ A , B CM bằng: A. 90 . B. 45 . C. 120 . D. 60 . Lời giải
Tác giả:Nguyễn Thành Đô ; Fb: Thành Đô Nguyễn Chọn A A M C B D
Vì tam giác ABC đều nên: AB ⊥ CM AB ⊥ CM  ( A , B CM ) = 90 .  Câu 9.
Chọn mệnh đề đúng trong các mệnh đề sau: Trong không gian
A. Ba véctơ đồng phẳng khi và chỉ khi ba véc tơ phải nằm trong cùng một mặt phẳng.
B. Ba véctơ đồng phẳng khi và chỉ khi giá của ba véctơ đó song song với nhau .
C. Ba véctơ đồng phẳng khi và chỉ khi ba véctơ cùng hướng.
D. Ba véctơ đồng phẳng khi và chỉ khi giá của ba véctơ cùng song song với một mặt phẳng Lời giải
Tác giả: Nguyễn Thành Trung ; Fb:Nguyễn Thành Trung Chọn D
Theo định nghĩa 3 véctơ gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.
Câu 10. Cho hình chóp S.ABC có SA ⊥ ( ABC ) và AB ⊥ BC . Gọi H là hình chiếu vuông góc của A
lên SB khẳng định nào sau đây là đúng?
A. AH ⊥ SC .
B. AH ⊥ AC .
C. AH ⊥ AB .
D. AH ⊥ ( SAC ) . Lời giải
Tác giả: Nguyễn Thành Trung ; Fb:Nguyễn Thành Trung Chọn A
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 9 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 S H A C BBC ⊥ AB Ta có   BC ⊥ (SAB) BC ⊥ SAAH ⊥ SB Suy ra 
AH ⊥ (SBC)  AH ⊥ AC . AH ⊥ BC 1 1 1
Câu 11. Tính giới hạn của dãy số u = + +...+ n 2 1 + 2 3 2 + 2 3 (n+ ) 1 n + n n +1 4 2 3 A. . B. . C. 1. D. . 5 3 2 Lời giải
Tác giả:Phạm Văn Tuấn ; Fb: Phạm Tuấn Chọn C Ta có: + −
( n+1+ n)( n+1− 1 1 n n n ) 1 1 = = = − ( . n + ) 1 n + n n +1
n n +1 ( n +1 + n )
n n +1 ( n +1 + n ) n n +1
Áp dụng kết quả trên cho u ta được: n 1 1 1 1 1 1 1 u = − + − +...+ − =1− . n 1 2 2 3 n n +1 n +1   Khi đó 1 lim u = lim 1− . n    n +1  1 1 n. 1 n n 0 Mà lim1 = 1 và lim = lim = lim = = 0 . Vậy limu =1. n n +1 1 1 1 n 1+ 1+ n n
Câu 12. Dãy số nào sau đây có giới hạn bằng 0 ? 2 n n n − 3n  6   2  A. 2 n − 4n . B. . C.   . D. −   . n +1  5   3  Lời giải
Tác giả:Phạm Văn Tuấn ; Fb:Phạm Tuấn
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 10 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 Chọn D n   Ta có lim n
q = 0 nếu q  1 . Do đó 2 lim − = 0   . n→+ n→+  3  Câu 13. Cho các khẳng định:
(I) Cho hàm số y = f ( x) liên tục trên a;b và f (a). f (b)  0 . Khi đó phương trình
f ( x) = 0 có ít nhất một nghiệm trên khoảng ( ; a b) .
(II) Cho hàm số y = f ( x) liên tục trên a;b và f (a). f (b)  0 . Khi đó phương trình
f ( x) = 0 không có nghiệm trên khoảng ( ; a b) .
Trong các khẳng định trên: A. Chỉ (I) đúng.
B. Cả (I), (II) đúng. C. Cả (I), (II) sai. D. Chỉ (II) đúng. Lời giải Chọn A
(I) Đúng theo định lý 3 – SGK tr 138.
(II) Sai. Vì ví dụ như hàm số f ( x) 2
= x −1 liên tục trên −2;2 và f (−2). f (2) = 9  0 nhưng
f ( x) = 0 có nghiệm −1,1 ( 2 − ;2) . Câu 14.
Cho hàm số f ( x) có đồ thị như hình vẽ Chọn đáp án đúng
A. Hàm số f ( x) gián đoạn tại x = 1 − .
B. Hàm số f ( x) liên tục tại x = 1 − .
C. Hàm số f ( x) liên tục trên khoảng (−3; ) 1 .
D. Hàm số f ( x) liên tục trên . Lời giải Chọn A
Nhìn vào đồ thị ta thấy tại x = 1
− đồ thị hàm số bị gián đoạn. Câu 15. TCho hình hộp ABC . D A BCD
  . Một đường thẳng  cắt các đường thẳng AA , BC,C D   lần lượt MA
tại M , N , P sao cho NM = 3NP . Tính k = MA .
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 11 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 2 2 A. k = . B. k = 2 . C. k = 3. D. k = . 3 3 Lời giải
Tác giả: Trương Thanh Nhàn; Fb: Trương Thanh Nhàn. Chọn D C B N D A B' C' P A' D' M
Giả sử MA = mAA ,
NB = nBC, PC = pD C   với , m , n p  . Ta có:
NB = nBC NA + AB = n AD NA = − AB + n AD PC = pD C
   PA + AC = pAB PA = −AC + pAB PA = −AA + ( p − ) 1 AB − AD
NM = NA − MA = −m AA − AB + n AD
NP = NA − MA = −m AA − AB + n AD
NM = 3NP  −m AA − AB + n AD = 3AA − 3 p AB + 3(n + ) 1 AD (1) Do AA ;  ;
AB AD là các vectơ không đồng phẳng nên  m = 3 − −m = 3  ( )   1 1   1 − = 3
− p   p =   n = (n +  ) 3 3 1  3 n = −  2 Do đó 3 3 3 MA = 3
− AA  MA = MA  MA = MA  k = . 2 2 2 Câu 16.
Cho u, v bất kì, chọn mệnh đề đúng?
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 12 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 u v u v A. (u v) . cos , = . B. .
u v = u . v .cos (u,v) . C. . u v = .
u v .cos (u,v).D. (u v) . cos , = . . u v u . v Lời giải
Tác giả: Trương Thanh Nhàn; Fb: Trương Thanh Nhàn. Chọn B
Dựa vào định nghĩa ta có ngay đáp án B đúng. Câu 17. ( 2018 2019 lim 4 − n − n ) bằng A. 0 . B. − . C. 2019 − . D. + . Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ Chọn B   4 1  Ta có lim ( 2018 2019 4 − n − n ) 2019 = lim n . − −1    . 2019   n n   4 1    4 1  Vì 2019 lim n = + và lim − −1 = 1 −  0   nên 2019 lim n . − −1 = −    . 2019  n n  2019   n n 
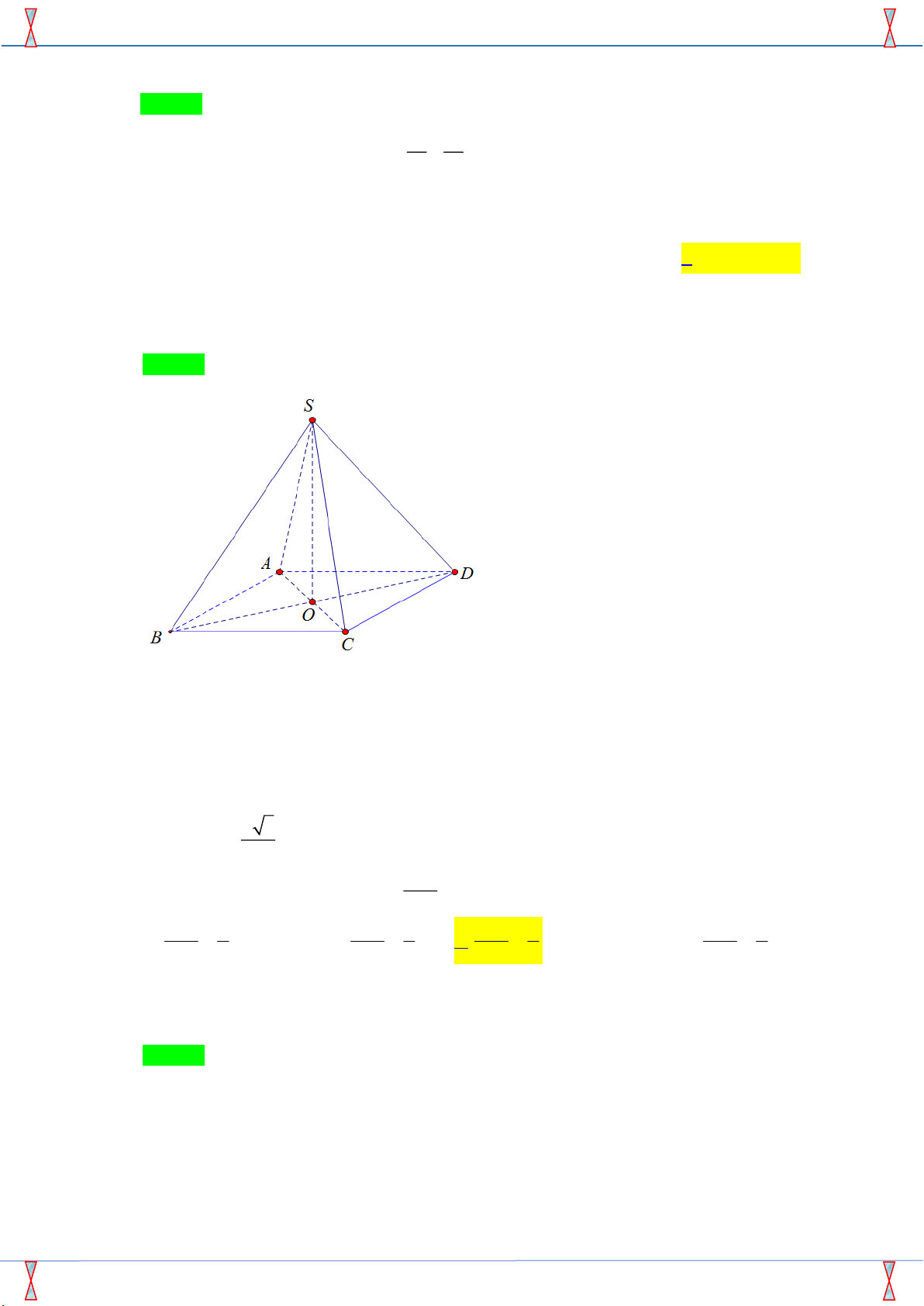
Câu 18. Cho hình chóp tứ giác S.ABCD , có đáy ABCD là hình vuông cạnh a , các cạnh bên đều bằng
a 2 . Góc giữa cạnh bên SB và mặt phẳng ( ABCD) bằng A. 0 30 . B. 0 60 . C. 0 90 . D. 0 45 . Lời giải
Tác giả: Vũ Danh Được; Fb: Danh Được Vũ Chọn D S A D O B C
Gọi O là giao điểm của AC và BD . Tam giác SAC cân tại S và O là trung điểm của AC
nên SO ⊥ AC . Tương tự ta có SO ⊥ BD . SO ⊥ ACSO ⊥ BD    ⊥ . AC BD  
( ABCD) SO ( ABCD) ,
AC BD = O
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 13 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Suy ra BO là hình chiếu vuông góc của BS trên mặt phẳng ( ABCD) . Do đó ( BD a 2 S ,
B ( ABCD)) = (S ,
B BO) = SBO . Ta có BO = = . 2 2 a 2 BO 1
Tam giác SBO vuông tại O nên 2 0 cos SBO = = =  SBO = 60 . SB a 2 2 Câu 19. Rút gọn 2 4 6 2 =1+ sin + sin + sin +...+ sin n S x x x
x + ... với sin x  1  . 1 A. 2 S = cos x . B. 2 S = tan x . C. S = S = + x . 2 1+ . D. 2 1 tan sin x Lời giải
Tác giả: Nguyễn Đức Hoạch; Fb: Hoạch Nguyễn Chọn D Ta có: 2
sin x  1 với mọi sin x  1  . 2 4 6 2  =1+ sin + sin + sin +...+ sin n S x x x
x + ... chính là tổng của cấp số nhân lùi vô hạn với công bội 2
q = sin x và u = 1. 1 u 1 1 1 2  S = = = = tan x +1. 2 2 1− q 1− sin x cos x   a
Câu 20. lim  x + 3x + 5x + 7x + ... 2019x − x  =
(với a , b nguyên dương nhỏ nhất). Tính x→+   b   a + b . A. 6 . B. 5 . C. 3 . D. 4 . Lời giải Chọn B  
Ta có: lim  x + 3x + 5x + 7x + ... 2019x − x x→+      
x + 3x + 5x + 7x +... 2019x − x  = lim   x→+  
x + 3x + 5x + 7x +... 2019x + x      
3x + 5x + 7x + ... 2019x  = lim   x→+  
x + 3x + 5x + 7x +... 2019x + x       5 7 2019   3 + + + ...+  1009 3 2 1 x xx −  3 = lim =   . x→+ 2  3 5 7 2019   1+ + + + ...+ +1 1010 3 7 2 1  x x x x −   
a = 3, b = 2  a +b = 5.
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 14 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 2  x − 3x + 2  khi x  2
Câu 21. Tìm a để hàm số f (x) =  x − 2 liên tục trên R.
 ax + a −5 khi x  2 A. 1. B. 3. C. 0. D. 2. Lời giải
Tác giả: Tạ Minh Trang; Fb: Minh Trang Chọn D 2 x − 3x + 2 Với x  ( ;
− 2) , f (x) = ; − 2 . x − liên tục trên ( ) 2
Với x  (2; +) , f (x) = ax + a − 5 liên tục trên (2; +) .
Với x = 2 , ta có f (2) = 3a − 5 và
lim f (x) = lim (ax + a − 5) = 3a − 5; + + x→2 x→2 2 x − 3x + 2
(x − )1(x −2) lim f (x) = lim = lim = lim (x − ) 1 = 1 − − − − x→2 x→2 − x→2 − . x→2 x 2 x 2
Hàm số f (x) liên tục trên R  3a − 5 = 1  a = 2 .  x +1 −1  khi x  0 
Câu 22. Cho hàm số ( ) x f x = 
. Chọn khẳng định đúng? 1  khi x = 0  2
A. Hàm số gián đoạn tại x = 0 .
B. Hàm số liên tục trên R.
C. Hàm số liên tục trên  1 − ;+) .
D. Hàm số liên tục trên (−3, 2) . Lời giải
Tác giả: Tạ Minh Trang; Fb: Minh Trang Chọn C x +1 −1
Với x  (−1;0)  (0; +) , f (x) =
liên tục trên khoảng (−1;0)  (0; +) . x 1 x +1 −1 x +1−1 1 1
Với x = 0, f (0) =
và lim f (x) = lim = lim = lim = . 2 x→0 x→0 x→0 x
x ( x +1 + ) x→0 1 x +1 +1 2
Do đó hàm số liên tục tại x = 0 . x +1 −1
Mặt khác lim f (x) = lim =1 và f ( 1
− ) =1. Suy ra hàm số liên tục phải tại −1. + + x→ 1 − x→ 1 − x
Vậy hàm số liên tục trên  1 − ;+) .
Câu 23. Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a 2 và BC = 2a . Khi đó góc giữa hai
đường thẳng AC và SB bằng A. 30 . B. 90 . C. 45 . D. 60 . Lời giải
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 15 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Tác giả: Phạm Văn Ninh; Fb: Ninh Phạm Văn Chọn D
Từ giả thiết ta có tam giác SBC vuông tại S . 2 a Ta có A .
C SB = SB (SC − SA) = S . B SC − S . B SA = −S . B SA = − . 2  ( 1 AC SB) AC.SB cos , = = −
 ( AC, SB) =120 . AC . SB 2
Vây góc giữa giữa hai đường thẳng AC và SB bằng 60 .
Câu 24. Cho hình chóp S.ABCD có đáy là hình vuông ABCD và SA vuông góc với mặt phẳng đáy
( ABCD) . Một mặt phẳng ( ) đi qua A và vuông góc với SC cắt hình chóp theo thiết diện là:
A. hình thoi có một góc có số đo bằng 60 . B. hình vuông. C. hình bình hành.
D. tứ giác có hai đường chéo vuông góc. Lời giải
Tác giả: Phạm Văn Ninh; Fb: Ninh Phạm Văn Chọn D
Gọi O là giao điểm của AC và BD . Từ A dựng AC ⊥ SC , gọi I = AC  SO . BD ⊥ SA  Vì
  BD ⊥ SC , mà BD ( ) , SC ⊥ ( )  BD // ( ) . BD ⊥ AC
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 16 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Vậy ( ) cắt ( SBD) theo giao tuyến đi qua I và song song với BD cắt SB , SD lần lượt tại
B , D  thiết diện của hình chóp cắt bởi ( ) là tứ giác AB CD  .
BD ⊥ (SAC ) Ta có:   B D
  ⊥ (SAC) , AC  (SAC)  B D
  ⊥ AC  thiết diện có hai BD // B D    đường chéo vuông góc.
Câu 25. Cho tứ diện ABCD . Gọi M , N ,G lần lượt là trung điểm của AB, CD, MN . Chọn khẳng định đúng: 1
A. GA + GB + GC + GD = 2MN . B. MN = (AD+CB). 2 1 1 C. MN = (AC +BD). D. MN = (AB+CD) 2 2 Lời giải
Tác giả: Phan Dung ; Fb: dungphan Chọn C Ta có:
AC + BD = AM + MN + NC + BM + MN + ND
= ( AM + BM )+(NC + ND)+ 2MN = 0 + 0 + 2MN. 1
MN = ( AC + BD) (đpcm). 2
(M , N lần lượt là trung điểm của AB, CD nên AM + BM = 0, NC + ND = 0) .
3 5x + 3 − x + 3 5 1 Câu 26. lim = − ( với ,
m n là các số nguyên dương). Tính m − n ? 2 x 1 → x −1 m n A. 15. B. 14. C. 12. D. 16. Lời giải
Tác giả: Phan Dung ; Fb: dungphan Chọn D + − − + − x + − x + (3 3 5x 3 2) ( x 3 2 5 3 3 ) 3 5x + 3 − 2 x + 3 − 2 lim = lim = lim − lim 2 2 2 2 x 1 → x 1 → x 1 → x 1 x −1 x −1 x −1 → x − . 1 3 5x + 3 − 2 5( x − ) 1 +) lim =lim 2 → − 1 → x 1 x x
(x − )1( 5x+3)2 1 2 3 3 + 2 5x + 3 + 4) 5 5 = lim =
x→ (x + )( x+ )2 1 3 3 + x + + ) 24 1 5 3 2 5 3 4 x + 3 − 2 x −1 1 1 +) lim = lim = lim = 2 x 1 → x 1 x −1 → ( 2 x − )
1 ( x + 3 + 2) x 1 → (x + ) 1 ( x + 3 + 2) 8
Nên suy ra: m = 24, n = 8  m − n = 16 .
Câu 27 . Cho hình lập phương ABC .
D EFGH . Hãy xác định góc giữa cặp véctơ AC và DE ?
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 17 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 A. 120 . B. 45 . C. 60 . D. 90 . Lời giải
Tác giả: Phan Chí Dũng ; Fb: Phan Chí Dũng Chọn A
Ta có góc giữa AC và DE bằng góc giữa AC và CF .
Dựng CK = AC suy ra góc giữa AC và CF bằng góc giữa CK và CF bằng góc FCK .
Xét tam giác AFC , ta có AC = AF = FC suy ra tam giác AFC là tam giác đều, suy ra góc
ACF = 60  FCK = 120 .
Vậy góc giữa AC và CF bằng 120 hay góc giữa AC và DE bằng 120 . x + 5 Câu 28 . lim bằng − x 3 → x − 3 15 A. − . B. − . C. 1. D. + . 2 Lời giải
Tác giả: Phan Chí Dũng ; Fb: Phan Chí Dũng Chọn B
Ta có lim ( x − 3) = 0 và x − 3  0 với x   3. − x 3 → x + 5
lim ( x + 5) = 3 + 5 = 8  0 . Suy ra lim = − . − − x 3 → x 3 → x − 3
Câu 29. Cho tứ diện đều ABCD cạnh a . Góc giữa AB và CD bằng: A. 0 60 . B. 0 30 . C. 0 90 . D. 0 45 . Lời giải
Tác giả: Trần Thị Thủy ; Fb: Trần Thủy Chọn C
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 18 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Gọi M là trung điểm của CD . Do các tam giác ACD và BCD là các tam giác đều nên ta có : AM ⊥ CD
CD ⊥ (ABM ) (1) BM ⊥ CD
Do AB  ( ABM ) (2)
Từ (1) và (2) ta có CD ⊥ AB nên góc giữa hai đường thẳng AB và CD bằng 0 90 x + 2m khi x  0
Câu 30. Tìm m để hàm số f (x) =  liên tục tại x = 0 2
x + x +1 khi x  0 1 1 A. m = . B. m = 1. C. m = . D. m = 0. 4 2 Lời giải
Tác giả: Trần Thị Thủy ; Fb: Trần Thủy Chọn C
Ta có lim f (x) = lim (x + 2 )
m = 2m ; f (0) = 1 và 2
lim f (x) = lim (x + x +1) = 1 − − + + x→0 x→0 x 0 → x 0 → Để 1
hàm số liên tục tại x = 0 điều kiện là: lim f (x) = lim f (x) = f (0)  2m = 1  m = − + x→0 x→0 2 Chọn đáp án C. Câu 31 . x + − bằng →+ ( 2 lim x 3 x x ) 3 A. + . B. . C. 3 . D. 0 . 2 Lời giải
Tác giả: Mai Ngọc Thi ; Fb: Mai Ngọc Thi Chọn B 2 2 x + 3 − x 3x 3x x + − = lim x = lim = lim →+ ( 2 lim x 3 x x
) x→+ 2x+3+x x→+ 2x+3+x x→+  3  x  1 + + 1 2 x   3 = 3 lim = . x→+ 3 2 1 + + 1 2 x
Câu 32. Tìm khẳng định sai trong các khẳng định sau :
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 19 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
A. G là trọng tâm tam giác ABC GA + GB + GC = 0 .
B. I là trung điểm của AB MA + MB = 2MI , M .
C. G là trọng tâm tam giác ABC MA + MB + MC = 3MG , M  . D. ABC . D '
A B' C' D' là hình hộp. Khi đó ta có : AB + AD + A ' A = AC . Lời giải
Tác giả: Mai Ngọc Thi ; Fb: Mai Ngọc Thi Chọn D Ta có ABC . D '
A B' C' D' là hình hộp nên ABCD là hình bình hành nên : AB + AD = AC nên
AB + AD + A ' A = AC là sai. Câu 33. 2 lim (x − 4) bằng: x→ 3 A. 2 . B. 1. C. 4 − . D −1. Lời giải
Tác giả, Fb: Lê Tuấn Duy Chọn D
Ta có : lim (x − 4) = ( 3)2 2 − 4 = 1. − x→ 3
Câu 34. Cho lăng trụ tam giác AB . C A BC  có AA' = , a AB = ,
b AC = c .Hãy biểu diễn vectơ B C  theo các vectơ , a , b . c A. B C
 = a + b − c . B. B C
 = −a + b − c . C. B C
 = a − b + c D. B C
 = a − b + c . Lời giải
Tác giả, Fb: Lê Tuấn Duy Chọn C
Ta có : B 'C = AC − AB ' = AC − (A B  − A'A)
= A'A − AB + AC = −a − b + c . Vậy: B C
 = −a −b + c
(1+ x)(1+ 2x)(1+3x)...(1+ 2019x)−1 Câu 35. lim bằng x→0 x
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 20 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 A. 2018.2019 . B. 1009.2019 . C. 1010.2019 . D. 0 . Lời giải
Tác giả: Bùi Bài Bình ; Fb: Bui Bai Chọn C
Đặt f ( x) = (1+ x)(1+ 2x) (1+ 2019x) −1 2019 2018 2 = a x + a x
+ + a x + a x +1−1 2019 2018 2 1 2019 2018 2 = a x + a x + + a x + a x . 2019 2018 2 1 f ( x) Suy ra 2018 2017 = a x + a x + + a x + a . 2019 2018 2 1 x 2019(1+ 2019) Với a = 1+ 2 + 3 + + 2019 = =1010.2019 . 1 2 f ( x) Vậy lim = lim( 2018 2017 a x + a x
+ + a x + a = a =1010.2019 . 2019 2018 2 1 ) 1 x→0 x→0 x 2
x + ax + b khi x 1  2  −
Câu 36. Biết hàm số f ( x) x 1 = 
(a,bR) liên tục tại x =1. Hãy tính S = 2a + 5b 1 − khi x =1  2 A. S = 10 . B. S = 7 . C. S = 4 . D. S = 2 . Lời giải
Tác giả: Bùi Bài Bình ; Fb: Bui Bai Chọn C
Điều kiện cần: Giả sử hàm số liên tục tại x =1. 2 2
x + ax + b
x + ax + b 1 Suy ra lim = f 1  lim = − . 2 ( ) 2 x 1 → x 1 x −1 → x −1 2 Suy ra phương trình 2
x + ax + b = 0 có nghiệm x = 1
1+ a + b = 0  b = −a −1. Ta có: + + − + + + + + f ( x) 2 x ax b (x ) 1 ( x a ) 1 x 1 a 2 a lim = lim = lim = lim = . 2 x 1 → x 1 → x 1 x −1 → (x − ) 1 ( x + ) x 1 1 → x +1 2 1
Mà lim f ( x) = − x 1 → 2 2 + a 1 Suy ra = −  a = 3 − , b = 2 . 2 2 2 x − 3x + 2 x −1 x − 2 x − 2 1
Thử lại: lim f ( x) ( )( ) = lim = lim = lim = − = f 1 . 2 x 1 → x 1 → x 1 x −1 → ( x − ) 1 ( x + ) ( ) x 1 1 → x +1 2 Vậy a = 3
− , b = 2 và S = 2a +5b = 6 − +10 = 4 .
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 21 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 2 x − 3x + 2 Câu 37. lim bằng x 1 → x −1 A. −1. B. 2 − C. 2. D. 1. Lời giải
Tác giả: Quỳnh Thụy Trang; Fb: XuKa Chọn A 2 x − 3x + 2
(x −1)(x − 2) lim = lim = lim(x − 2) = 1 − . x 1 → x 1 → x 1 x −1 x −1 →
Câu 38. Cho f (x) liên tục trên −1;5 thỏa mãn f ( 1
− ) =1, f (5) = 6 . Phương trình nào sau đây luôn có
nghiệm trong khoảng (−1;5) ?
A. f (x) = 8 .
B. f (x) = 3 .
C. f (x) + 5 = 0 .
D. f (x) = 1 . Lời giải
Tác giả: Quỳnh Thụy Trang ; Fb: XuKa Chọn B
Gọi g ( x) = f ( x) − 3 Ta có g (− ) 1 = f (− ) 1 − 3 = 2 −  0
g (5) = f (5) − 3 = 3  0  g (− ) 1 .g (5)  0
g ( x) = 0 luôn có nghiệm trong khoảng ( 1 − ;5)
f ( x) = 3 luôn có nghiệm trong khoảng ( 1 − ;5)
Câu 39. Giá trị của ( 2 lim
4n + 5n +1 − 2n) bằng : 5 5 A. − . B. . C. + . D. . 2 4 Lời giải
Tác giả: Nguyễn Thùy Linh ; Fb: Nguyễn Thùy Linh Chọn D
n + n + − n
n + n + + n n +
lim ( 4n + 5n +1 − 2n) ( 2 4 5 1 2 ).( 2 4 5 1 2 5 1 2 ) = lim = lim 2 2
4n + 5n +1 + 2n
4n + 5n +1 + 2n 1 5 + 5 = lim n = . 5 1 4 4 + + + 2 2 n n Câu 40. ( 2 4
lim 5 − 3x − 2019x ) bằng x →− A. − . B. − 3 . C. − 2019 . D. + . Lời giải
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 22 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Tác giả: Nguyễn Thùy Linh ; Fb: Nguyễn Thùy Linh Chọn A    lim ( 5 3 2 4
5 − 3x − 2019x ) 4 = lim x − − 2019 = −    . 4 2 x →− x →−   x x 
Câu 41. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O . Biết SA = SC, SB = SD . Khẳng
định nào sau đây sai?
A. SO ⊥ ( ABCD)
B. AC ⊥ (SBD) C. BD ⊥ (SAC )
D. AB ⊥ (SAD) Lời giải
Tác giả: Phạm Ngọc Hưng; Fb: Hưng Phạm Ngọc Chọn D
Khẳng định sai là AB ⊥ (SAD) .
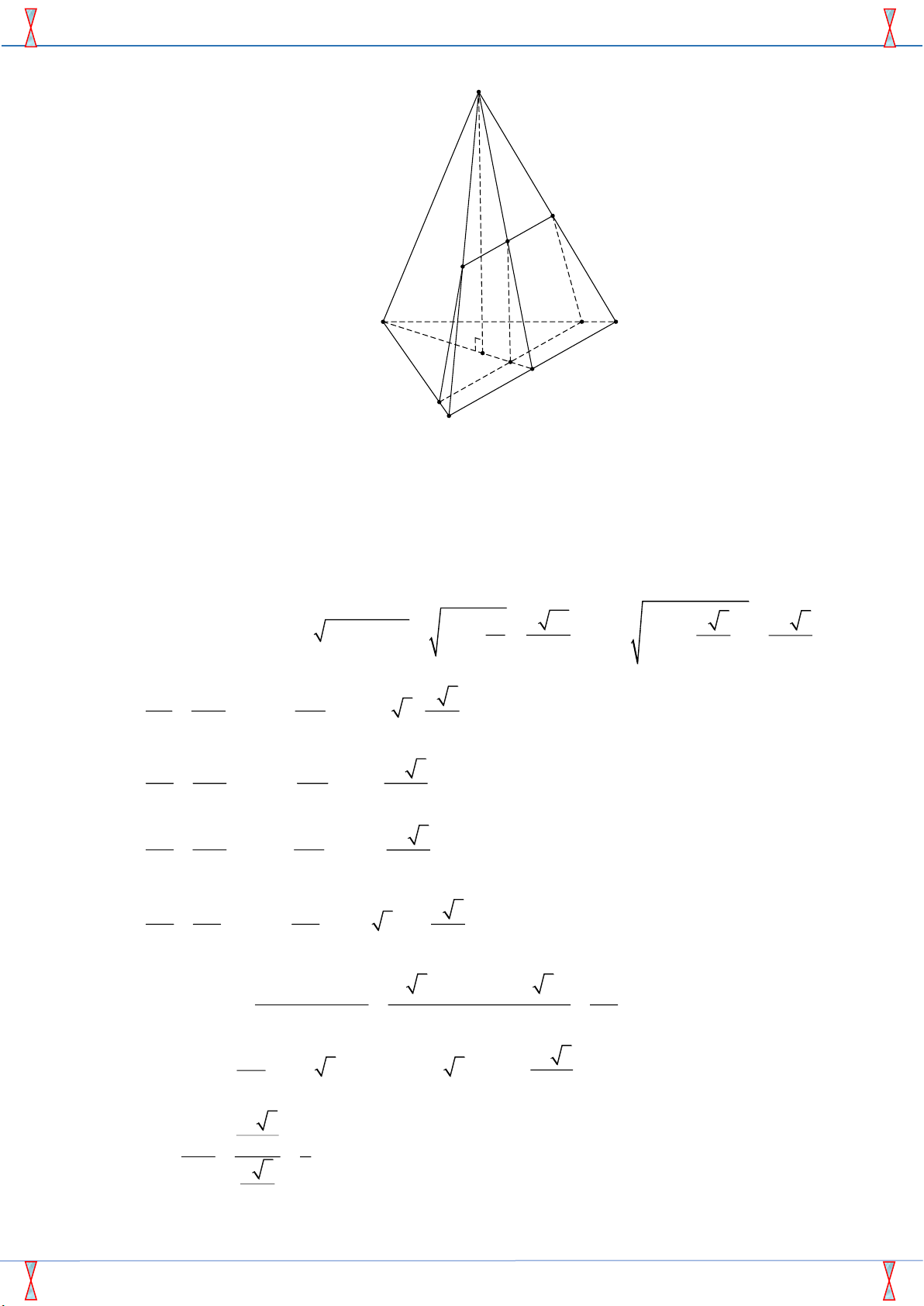
Câu 42. Cho hình chóp S.ABC , có đáy ABC là tam giác đều cạnh a . Gọi O là tâm đường tròn ngoại
tiếp tam giác ABC . Biết SO vuông góc với đáy ( ABC ) và SO = 2a . Gọi M là điểm thuộc
đường cao AH của tam giác ABC . Xét mặt phẳng (P) đi qua M và vuông góc với AH . Đặt a 3
AM = x, x
. Xác định vị trí điểm M để thiết diện của hình chóp cắt bởi mặt phẳng (P) 3 AM
có diện tích lớn nhất. Khi đó tỷ số bằng AH AM 4 AM 5 AM 3 AM 2 A. = B. = C. = D. = AH 5 AH 6 AH 4 AH 3 Lời giải
Tác giả: Phạm Ngọc Hưng; Fb: Hưng Phạm Ngọc Chọn C
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 23 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 S P I Q A C F O M H E B
Trong mặt phẳng ( ABC ) kẻ đường thẳng qua M và song song với BC cắt AB, AC lần lượt
tại E, F . Trong mặt phẳng ( SAH ) kể đường thẳng qua M và song song với SO , cắt SH tại
I . Trong mặt phẳng ( SBC ) kẻ đường thẳng đi qua I và song song với BC cắt SC, SB lần
lượt tại P,Q . Khi đó thiết diện cần tìm là hình thang EFPQ . 2 2 a a 39  a 3  7a 3 Ta có 2 2 2
SA = SB = SC = SO + AO = 4a + = , 2 SH = 4a +   = . 3 3   6 6   MI MH SOa 3  =  MI = .MH = 4 3  − x   . SO HO HO 2   EF AM BC 2x 3 =  EF = .AM = . BC AH AH 3 HI MH SH  7a 3  =  HI = MH =  − 7x   . SH HO HO 2   PQ SI BCa 3  =  PQ =
.SI = 2 3  x −    . BC SH SH 3   ( + )
( x− a)( a− x PQ EF MI ) 2 4 3 3 6 4 3 . Do đó 3a S = =  . EFPQ 2 3 4 2 3a 3a 3 maxS =
khi 4 3x − 3a = 6a − 4 3x x = . EFPQ 4 8 3a 3 AM 3 Vậy 8 = = . AH a 3 4 2
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 24 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 5x + 3 − 3 a
Câu 43. [Mức độ 2] lim =
(với a, b, c
). Tính a − b + c . x→0 x b c A. 0. B. 6. C. 8. D. 4. Lời giải
Tác giả: Phạm Chí Dũng ; Fb: Phạm Chí Dũng Chọn B 5x + 3 − 3 5x + 3 − 3 5 5 Ta có: lim = lim = lim = . x→0 x
x→0 x ( 5x + 3 + 3) x→0 5x + 3 + 3 2 3
Vậy a = 5 , b = 2 , c = 3. Suy ra: a − b + c = 6 .
Câu 44. [Mức độ 2] ( 3 lim 2
− 018x + 2x + 5) bằng x→− A. + . B. 0. C. − . D. 2018 − . Lời giải
Tác giả: Phạm Chí Dũng ; Fb: Phạm Chí Dũng Chọn D  2 5  Ta có: ( 3 lim 2
− 018x + 2x + 5) 3 = lim x 201 − 8 + +  . x→− 2 3 x→−  x x   2 5  Mà 3 lim x = − ; lim 201 − 8 + + = 201 − 8   . 2 3 x→− x→−  x x  Vậy ( 3 lim 2
− 018x + 2x + 5) = +. x→− x − x +
Câu 45. Hàm số f ( x) 2 4 3 = .không liên tục tại x − 2 A. x = 3. B. x = 2 . C. x = 1 . D. x = 0 . Lời giải
Tác giả: Diệp Tuân; Fb: Tuân Diệp Chọn B
Hàm số f ( x) có xác định D = \   2 .
Do x = 2 D nên hàm số f ( x) không liên tục tại x = 2 . 1− 3x Câu 46. lim .bằng
x→− 2x + 5 3 1 1 3 A. − . B. . C. . D. − . 2 5 2 5 Lời giải
Tác giả: Diệp Tuân; Fb: Tuân diệp Chọn B 1 −3 1− 3x 3 Ta có lim = lim x = − .
x→− 2x + 5 x→− 5 2 2 + x
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 25 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019 2 + 3n
Câu 47. Giá trị của lim 2
3n − n + bằng: 2 2 A. 1. B. . C. + . D. 0 . 3 Lời giải
Tác giả: Hà Lê; Fb: Ha Le Chọn D 2 3 + 2 2 + 3n 0 lim = lim n n = = 0 . 2 3n − n + 2 1 2 3 3 − + 2 n n
Câu 48. Cho hai đường thẳng phân biệt a , b và điểm O không thuộc mặt phẳng ( P) . Mệnh đề nào sau đây là sai ?
A. Nếu hai đường thẳng a và b cùng vuông góc với mặt phẳng ( P) thì chúng song song với nhau.
B. Nếu a / / b và a vuông góc với mặt phẳng ( P) thì b cũng vuông góc với mặt phẳng ( P) .
C. Có duy nhất một đường thẳng d đi qua điểm O và song song với mặt phẳng ( P) .
D. Có duy nhất một đường thẳng d đi qua điểm O và vuông góc với mặt phẳng ( P) . Lời giải
Tác giả: Hà Lê; Fb: Ha Le Chọn C
Mệnh đề A , B , D đúng (theo các tính chất đã biết).
Mệnh đề C sai vì qua một điểm nằm ngoài một mặt phẳng có vô số đường thẳng song song với mặt phẳng đó. n n+2 10 + 30 Câu 49. lim bằng 5.30n − 4.20n A. + . B. − . C. 900 . D. 180 . Lời giải
Tác giả: Đặng Ân ; Fb:Đặng Ân Chọn D n  1  + n n+2 900   10 + 30 10n + 900.30n  3  lim = lim = lim =180 . 5.30n − 4.20n 5.30n − 4.20n n  2  5 − 4.   3 
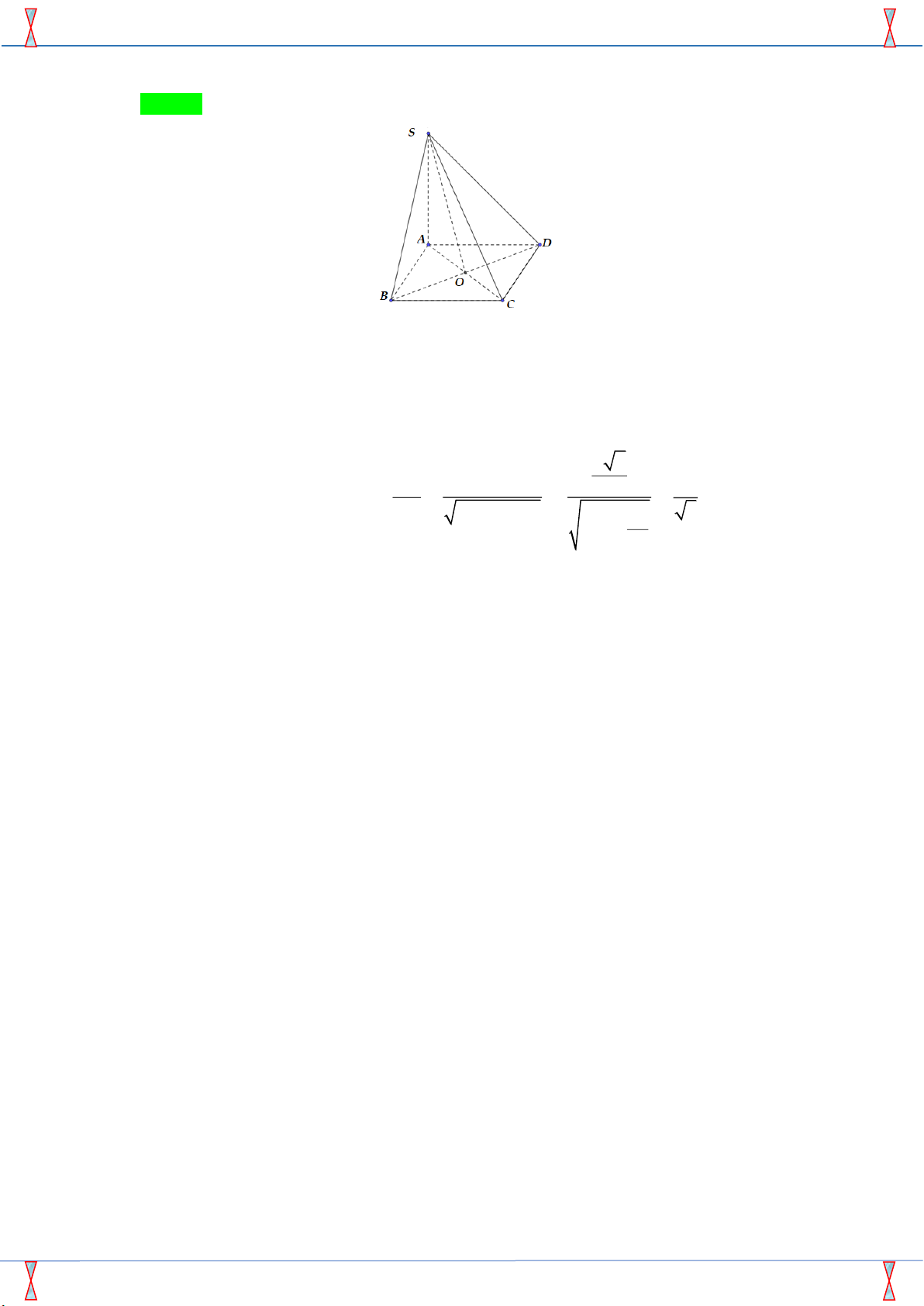
Câu 50. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA = a 2 và SA vuông góc
với mặt phẳng đáy ( ABCD) . Gọi  là góc giữa SB và mặt phẳng ( SAC ) . Tính tan . 1 1 1 A. tan  = . B. tan  = . C. tan = 2 . D. tan = . 5 3 2 Lời giải
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 26 Mã đề 1881
Sản phẩm của Group FB: STRONG TEAM TOÁN VD VDC
Đề Giữa HK2 Lớp 11- Việt Nam- Ba Lan 2019
Tác giả: Đặng Ân ; Fb:Đặng Ân Chọn A
Gọi O là giao điểm hai đường chéo của hình vuông ABCD .
BO⊥ACBO⊥(SAC)  SO là hình chiếu của SB lên mặt phẳng (SAC) BO ⊥ SA
 = (SB;SO) = BSO (do tam giác SBO vuông tại O nên BSO là góc nhọn). a 2 BO BO 1
Xét tam giác SBO có tan BSO = = 2 = = . SO 2 2 SA + AO 2 5 2 a 2a + 2
Chia sẻ bởi Quybacninh từ Gr FB: STRONG TEAM TOÁN VD-VDC
Trang 27 Mã đề 1881
Document Outline

  • [toanmath.com] - Đề kiểm tra giữa HK2 Toán 11 năm 2018 – 2019 trường Việt Nam – Ba Lan – Hà Nội
  • [STRONG TEAM TOÁN VD-VDC]-Đề kiểm tra giữa hk2 lớp 11 Việt Nam- Ba Lan 2018-2019