Đề kiểm tra giữa HK2 Toán 11 năm 2020 – 2021 trường THPT Thị xã Quảng Trị
Đề kiểm tra giữa HK2 Toán 11 năm học 2020 – 2021 trường THPT Thị xã Quảng Trị gồm 01 trang với 06 bài toán dạng tự luận, thời gian học sinh làm bài thi là 90 phút, đề thi có lời giải chi tiết và hướng dẫn chấm điểm.
Preview text:
SỞ GD-ĐT QUẢNG TRỊ ĐỀ KIỂM TRA GIỮA HỌC KỲ II
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ NĂM HỌC 2020 - 2021 Môn: Toán Lớp: 11 Đề KT chính thức
Thời gian làm bài: 90 phút, không kể thời gian giao đề (Đề có 01 trang) Mã đề: 01 u u 2
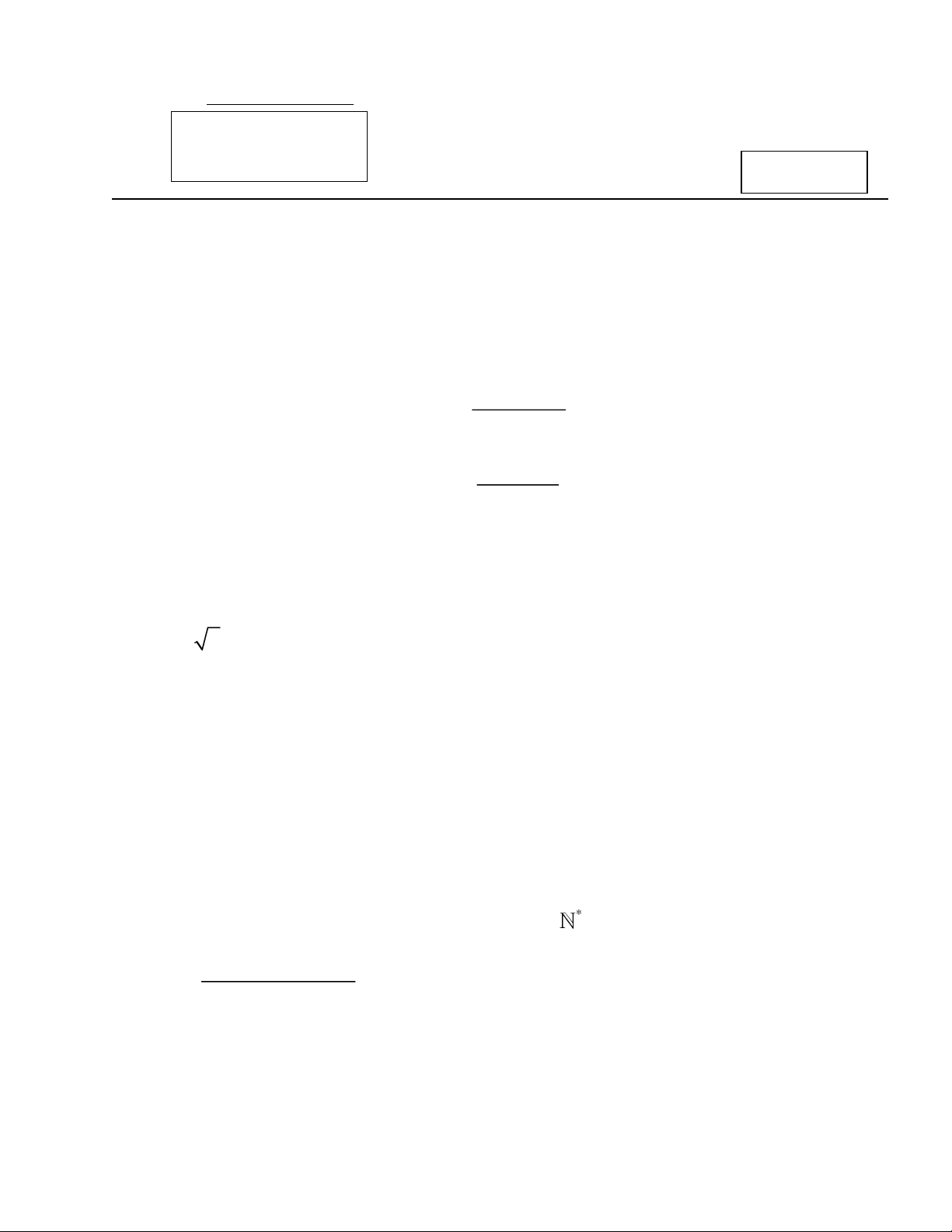
Câu 1 (2,0đ). Cho (un) là cấp số cộng có: 1 5 2u u 0 2 4
Tìm số hạng đầu u1 và công sai d của cấp số cộng đó. 2 2n n 1
Câu 2 (2,0đ). Tìm các giới hạn sau: a) lim 2 1 n 3n 3.4n b) lim 1 4n
Câu 3 (1,0đ). Tìm cấp số cộng gồm 3 số hạng, biết tổng của chúng bằng 21 và tích của chúng bằng 231.
Câu 4 (3,0đ). Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, tam giác SBD đều
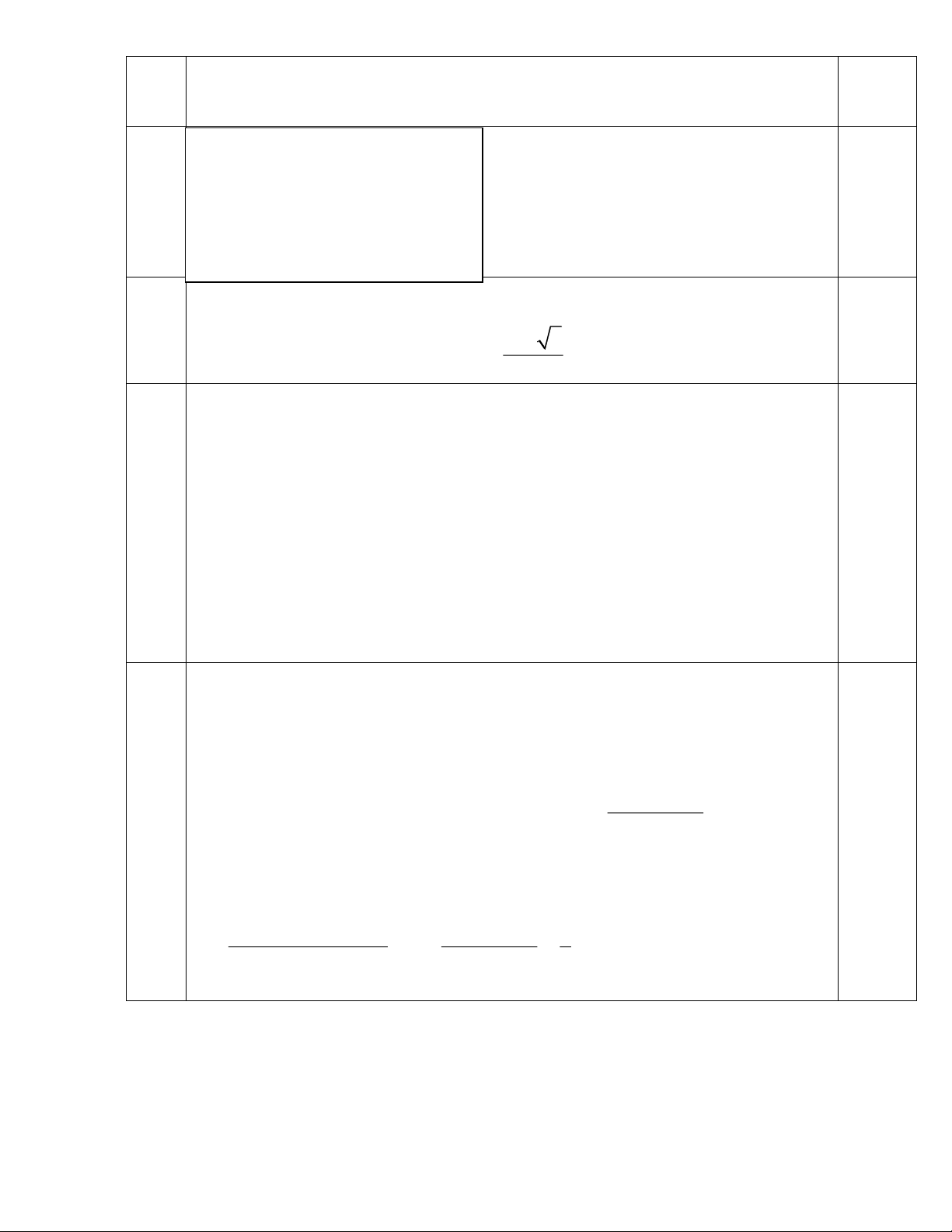
có cạnh a 2 . Gọi M, N, P lần lượt là trung điểm của AD, BC, SD.
a) Chứng minh rằng (MNP) / /(SAB).
b) Gọi G là trọng tâm tam giác BCD .Tìm thiết diện của hình chóp S.ABCD cắt bởi
mp( ) , biết mp( ) đi qua G và song song với (SBD).Tính diện tích của thiết diện.
Câu 5 (1,0đ). Một cấp số nhân gồm 3 số hạng có tổng bằng 26. Cũng theo thứ tự đó nếu
cộng thêm lần lượt 1; 7; 5 đơn vị vào 3 số hạng thì ta được số hạng thứ 1; 3; 5 của một cấp số
cộng. Tìm cấp số nhân đó.
u 1;u 2 0 1
Câu 6 (1,0đ). Cho (un) có: * u
2u u 5, n n 1 n n 1
2 4 6 ... 2n Tìm: lim un
-----------------HẾT---------------------
SỞ GD-ĐT QUẢNG TRỊ ĐỀ KIỂM TRA GIỮA HỌC KỲ II
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ NĂM HỌC 2020 - 2021 Môn: Toán Lớp: 11 Đề KT chính thức
Thời gian làm bài: 90 phút, không kể thời gian giao đề (Đề có 01 trang) Mã đề: 02 u u 8
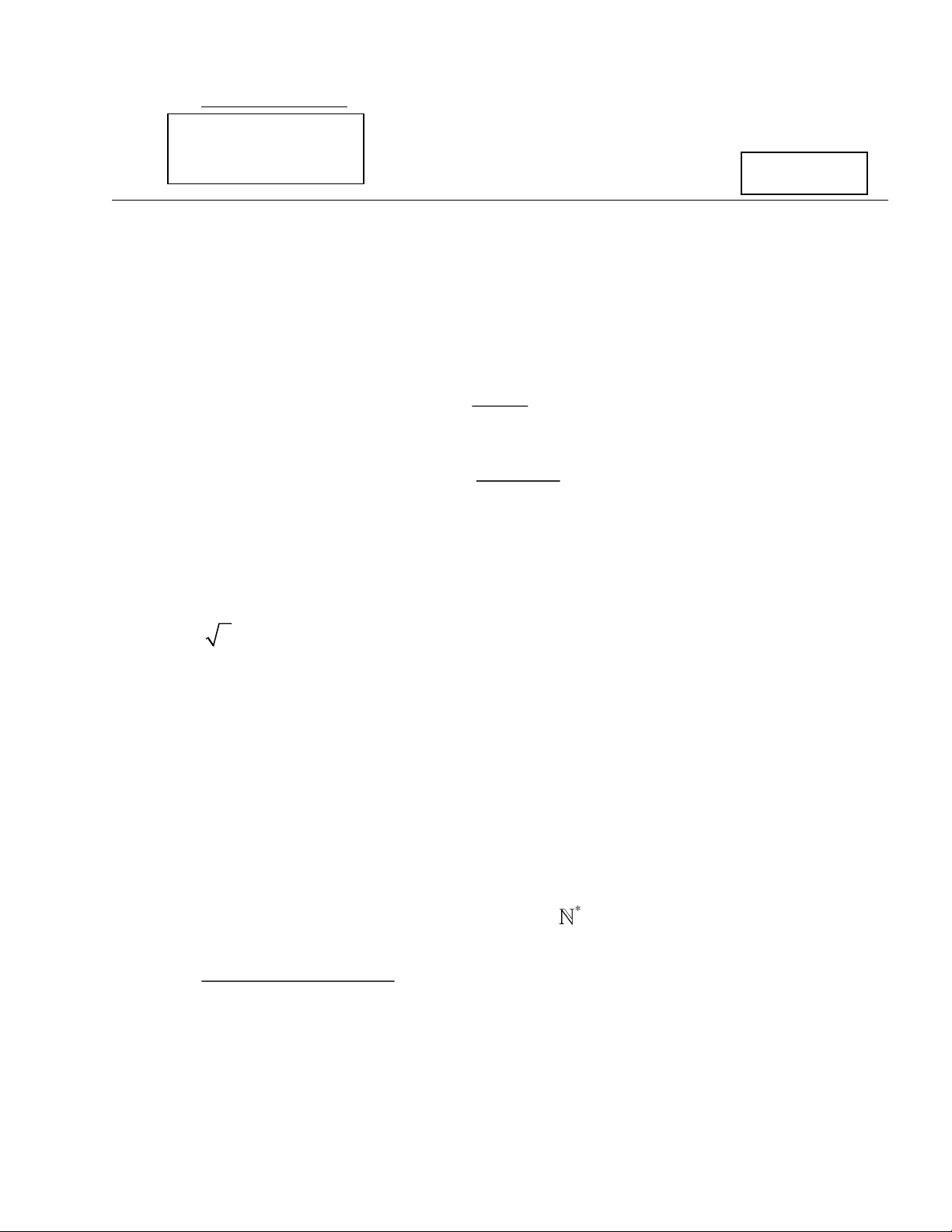
Câu 1 (2,0đ). Cho (un) là cấp số cộng có: 2 6 2u u 15 3 7
Tìm số hạng đầu u1 và công sai d của cấp số cộng đó. n 1
Câu 2 (2,0đ). Tìm các giới hạn sau: a) lim 5 2n 2n 4.5n b) lim 1 5n
Câu 3 (1,0đ). Tìm cấp số cộng gồm 4 số hạng, biết tổng của chúng bằng 10 và tổng các bình
phương của chúng bằng 70.
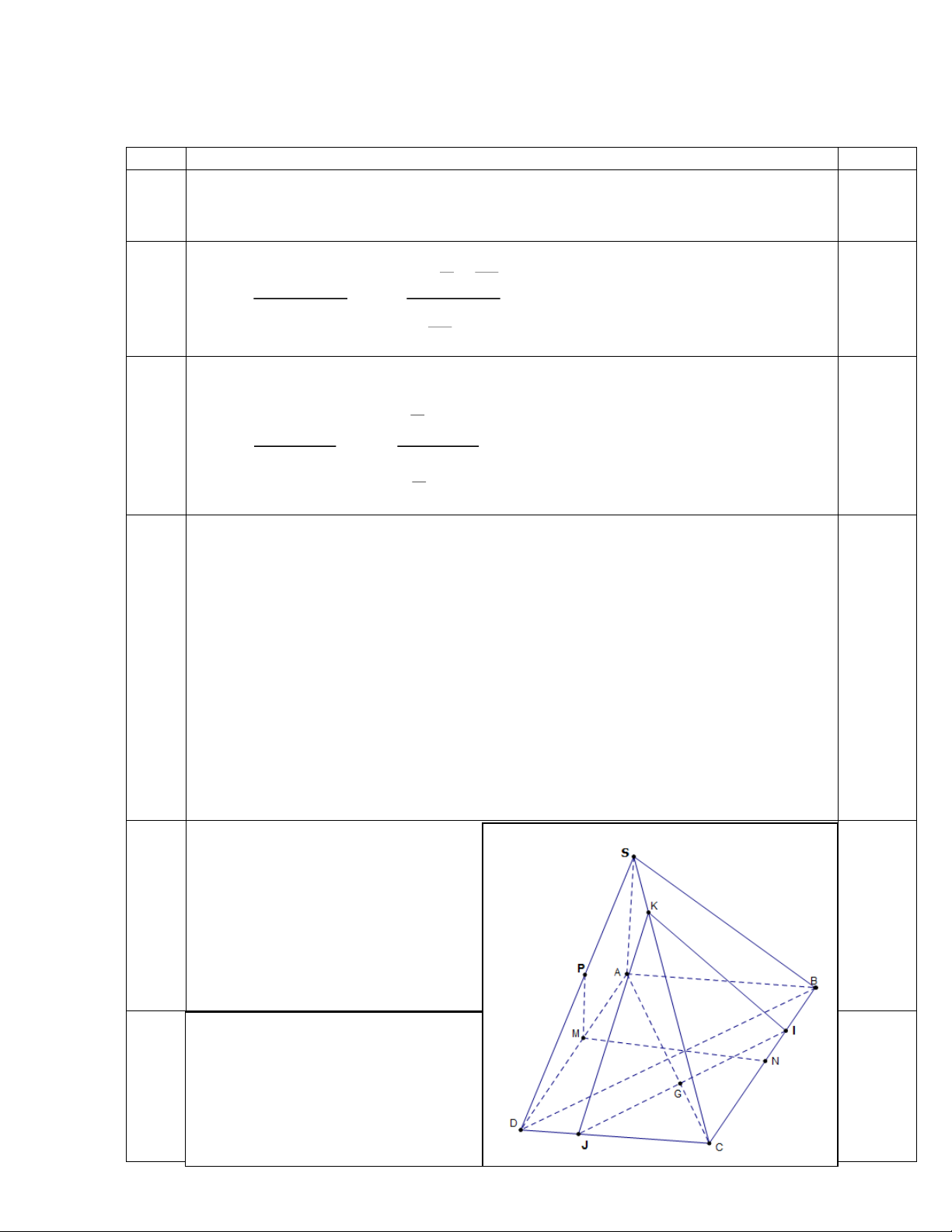
Câu 4 (3,0đ). Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, tam giác SAC đều
có cạnh 2a 2 . Gọi I, J, K lần lượt là trung điểm của SA, AD, BC.
a) Chứng minh rằng (IJK ) / /(SCD).
b) Gọi G là trọng tâm tam giác ABC .Tìm thiết diện của hình chóp S.ABCD cắt bởi
mp( ) , biết mp( ) đi qua G và song song với (SAC) .Tính diện tích của thiết diện.
Câu 5 (1,0đ). Một cấp số nhân gồm 3 số hạng có tổng bằng 21. Cũng theo thứ tự đó nếu cộng
thêm lần lượt 1; 7; 10 đơn vị vào 3 số hạng thì ta được số hạng thứ 1; 4; 7 của một cấp số
cộng. Tìm cấp số nhân đó.
u 1;u 2 0 1
Câu 6 (1,0đ). Cho (un) có: * u
2u u 3, n n 1 n n 1
1 3 5 ... 2n 1 Tìm: lim un
-----------------HẾT---------------------
ĐÁP ÁN KT GIỮA KỲ II NĂM HỌC 2020 - 2021 MÔN TOÁN KHỐI 11 MÃ ĐỀ 01 Câu Lời giải Điểm C1 u u 2
2u 4d 2 u 5 1 5 1 1 2.00đ 0.10đ 2u u 0 3u 5d 0 d 3 2 4 1 0.10đ C2.a 1 1 1.00đ 2 2 0.5đ 2 2n n 1 ) lim = lim n n a = -2 2 1 n 1 0.50đ 1 2 n C2.b 1.00đ n 3 3 3n 3.4n 4 0.5đ b) lim = lim 3 1 4n n 1 1 0.50đ 4 C3.
Gọi 3 số là a – d; a; a + d. Theo bài ra ra có 1.00đ 3 a 21 a 7 2 2
a(a d)(a d) 231
7(a d ) 231 0.25đ a 7 a 7 0.25đ 2 2 2 7(7 d ) 231 d 16
a 7 a 7 ; 0.25đ
d 4 d 4 0.25đ
Có 2 csc là 3;7;11 và 11; 7; 3. C4.a. MP / /SA 1.00đ
MP / /(SAB)(1) SA (SAB) 0.5đ MN / / AB
MN / /(SAB)(2) 0.25đ AB (SAB)
(1),(2) (MNP) / /(SAB) 0.25đ C4.b. 2.00đ 1.0 đ
Xác định đúng thiết diện là tam giác IKJ
C4.b. Chứng minh được tam giác IKJ đồng dạng với tam giác BSD theo tỉ số 2/3 0.5đ 2 a 3
Tính đúng diện tích tam giác IKJ bằng 0.5đ 9 C5.
Gọi 3 số hạng đó là u ;u ;u 1.00đ 1 2 3 1 u u2 3 u 26 2 u u u Theo giả thiết, ta có 1 3 2 u 2 1 u 2d 6 0.50đ 3 u 1 u 4d 4
u 18 u 2 Giải được 1 1 ; 0.25đ d 3 d 5
Tìm được 2 CSN là 18;2;6 và 2;6;18 0.25đ C6. 1.00đ Đặt v
là csc có số hạng đầu bằng 1 và công sai d = 5. 1 u 1 u (v ) n n n n 1 v 1 u 0 u 2 v u2 1 u 2 . 5n 3n 2 1 v 2 v ...v u 1 n n un . 2 0.5đ . n v un un 1 2 4 ... 2n 2 ( n n 1) 2 lim lim 2 n u 5n 3n 2 5 0.5đ
Ngoài cách giải mà đáp án nêu ra nếu học sinh có cách giải khác nếu đúng vẫn cho điểm tối đa. MÃ ĐỀ 02 Câu Lời giải Điểm C1 u u 8
2u 6d 8 2 6 1 2.00đ 0.10đ 2u u 15 3u 10d 15 3 7 1 0.10đ C2.a 1 1.00đ 1 n 1 1 0.5đ ) ) lim = lim n a a = 5 2n 5 2 0.50đ 2 n C2.b 1.00đ n 2 4 2n 4.5n 5 0.5đ b)b) lim = lim 4 1 5n n 1 1 0.50đ 5 C3.
Gọi 4 số là a – 3d; a-d; a + d; a+3d. Theo bài ra ra có: 1.00đ 5 4a 10 a 2 0.25đ
(a 3d)(a 3d)(a d)(a d) 70 2 2
4a 20d 70 5 0.25đ a 2 9 2 d 0.25đ 4 0.25đ 5 5 a a 2 2 ; 3 3 d d 2 2
Có 2 csc là -2;1;4;7 và 7; 4; 1; -2. C4.a. JI / /SD 1.00đ
JI / /(SCD)(1) S (SCD) 0.5đ JK / /CD
JK / /(SCD)(2) 0.25đ JK (SCD)
(1),(2) (IJK ) / /(SCD) 0.25đ C4.b. 2.00đ 1.0 đ
Xác định đúng thiết diện là tam giác MNP
C4.b. Chứng minh được tam giác MNP đồng dạng với tam giác SAC theo tỉ số 2/3 0.5đ 2 8a 3
Tính đúng diện tích tam giác MNP bằng 0.5đ 9 C5.
Gọi 3 số hạng đó là u ;u ;u 1.00đ 1 2 3 1 u u2 3 u 21 2 u u u Theo giả thiết, ta có 1 3 2 u 2 1 u 3d 6 0.50đ 3 u 1 u 6d 9
u 12 u 3 Giải được 1 1 ; 0.25đ
d 0 d 3
Tìm được 2 CSN là 12;6;3 và 3;6;12 0.25đ C6. 1.00đ Đặt v
là csc có số hạng đầu bằng 1 và công sai d = 5. 1 u 1 u (v ) n n n n 1 v 1 u 0 u 2 v u2 1 u 2 . 3n n 2 1 v 2 v ...v u 1 n n un . 2 0.5đ . n v un un 1
1 3 ... 2n 2 1 (n 1) 1 lim lim 2 u n 3n n 2 3 0.5đ
Ngoài cách giải mà đáp án nêu ra nếu học sinh có cách giải khác nếu đúng vẫn cho điểm tối đa.