Đề kiểm tra giữa học kỳ 2 Toán 11 năm 2018 – 2019 trường Nguyễn Chí Thanh – TP HCM

Giới thiệu đến thầy, cô và các em học sinh khối 11 nội dung đề kiểm tra giữa học kỳ 2 Toán 11 năm 2018 – 2019 trường Nguyễn Chí Thanh – thành phố Hồ Chí Minh, giúp các em có thêm đề thi ôn tập để chuẩn bị cho kỳ thi giữa HK2 Toán 11.

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 11

Môn: Toán 11

Thông tin:

4 trang 6 tháng trước

Tác giả:

Profile Kim Oanh
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM KIỂM TRA GIỮA HỌC KỲ II
TRƯỜNG THPT NGUYỄN CHÍ THANH Năm học: 2018 - 2019
Môn: TOÁN- Lớp 11
Thời gian: 60 phút (không kể thời gian phát đề)
Bài 1: (5,0 điểm) Tìm các giới hạn sau:
1)
x
x x
x x+
2
3
2
2 5 2
lim
2 4
→−
+ +
−
2)
2
2
2
5 3
lim
3 2
x
x
x x
→
− +
3)
2
2 5 3 1
lim
2 1
x
x x x
x
→−∞
− + + −
+
4)
(
)
2
lim 4 3 1 2
x
x x x
→+∞
− + − 5)
3
2
2 3 5
lim
3 2
x
x x
x x
→−∞
− +
− −
Bài 2: (1,0 điểm)
Cho hàm s
ố
(
)
2
2
f x x x
= − +
. Tìm a, b biết
x
f(x)
a lim
x
→−∞
= và
(
)
x
b lim f(x) ax
→−∞
= − .
Bài 3:(4,0 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA ⊥ (ABCD).
1) CMR: các tam giác SBC và SCD là các tam giác vuông.
2) Dựng AH là đường cao của tam giác SAD. Chứng minh:
AH SC
⊥
3) Gọi K là hình chiếu vuông góc của A lên SB. Chứng minh: (SAC) ⊥ (AHK).
4) Cho
2, , 3
SA a AB a AD a
= = =
. Tính góc hợp bởi SB và (SAC).
––––––––––––––––––––Hết–––––––––––––––––––
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM KIỂM TRA GIỮA HỌC KỲ II
TRƯỜNG THPT NGUYỄN CHÍ THANH Năm học: 2018 - 2019
Môn: TOÁN- Lớp 11
Thời gian: 60 phút (không kể thời gian phát đề)
Bài 1: (5,0 điểm) Tìm các giới hạn sau:
1)
x
x x
x x+
2
3
2
2 5 2
lim
2 4
→−
+ +
−
2)
2
2
2
5 3
lim
3 2
x
x
x x
→
− +
3)
2
2 5 3 1
lim
2 1
x
x x x
x
→−∞
− + + −
+
4)
(
)
2
lim 4 3 1 2
x
x x x
→+∞
− + − 5)
3
2
2 3 5
lim
3 2
x
x x
x x
→−∞
− +
− −
Bài 2: (1,0 điểm)
Cho hàm số
(
)
2
2
f x x x
= − +
. Tìm a, b biết
x
f(x)
a lim
x
→−∞
= và
(
)
x
b lim f(x) ax
→−∞
= − .
Bài 3:(4,0 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA ⊥ (ABCD).
5) CMR: các tam giác SBC và SCD là các tam giác vuông.
6) Dựng AH là đường cao của tam giác SAD. Chứng minh:
AH SC
⊥
7) Gọi K là hình chiếu vuông góc của A lên SB. Chứng minh: (SAC) ⊥ (AHK).
8) Cho
2, , 3
SA a AB a AD a
= = =
. Tính góc hợp bởi SB và (SAC).
––––––––––––––––––––Hết–––––––––––––––––––
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
ĐÁP ÁN ĐỀ KIỂM TRA GIỮA HỌC KÌ II – NĂM HỌC 2018 – 2019
MÔN TOÁN LỚP 11
Bài
Ý
NỘI DUNG
ĐIỂM
1
1)
x
x x
x x+
2
3
2
2 5 2
lim
2 4
→−
+ +
−
=
(
)
(
)
( )
( )
x
x x
x x x
2
2
2 2 1
lim
2 2 2
→−
+ +
+ − +
0,25+0,25
2
2
2 1
lim
2 2
x
x
x x
→−
+
=
− +
3
10
= −
0,25+0,25
2)
2
2
2
5 3
lim
3 2
x
x
x x
→
− +
=
( )
(
)
2
2
2 2
4
lim
3 2 5 3
x
x
x x x
→
−
− + + +
0,25
(
)
(
)
( )( )
(
)
2
2
2 2
lim
2 1 5 3
x
x x
x x x
→
− +
=
− − + +
0,25
( )
(
)
2
2
2
lim
1 5 3
x
x
x x
→
+
=
− + +
2
3
=
0,25+0,25
3)
2
2 5 3 1
lim
2 1
x
x x x
x
→−∞
− + + −
+
=
2
2 5
1 3 1
lim
2 1
x
x x
x x
x
→−∞
− − + + −
+
0,25
2
2 5 1
1 3
lim
1
2
x
x x x
x
→−∞
− − + + −
=
+
0,5
1
=
0,25
4)
(
)
2
lim 4 3 1 2
x
x x x
→+∞
− + − =
2 2
2
4 3 1 4
lim
4 3 1 2
x
x x x
x x x
→+∞
− + −
− + +
0,25
2
3 1
lim
3 1
4 2
x
x
x x
x x
→+∞
− +
=
− + +
0,25
2
1
3
lim
3 1
4 2
x
x
x x
→+∞
− +
=
− + +
3
4
= −
0,25+0,25
5)
3
2
2 3 5
lim
3 2
x
x x
x x
→−∞
− +
− −
=
2 3
2
3 5
2
lim .
3 1
2
x
x x
x
x x
→−∞
− +
− −
= +∞
0,5
Vì
2 3
2
lim
3 5
2
lim 1
3 1
2
x
x
x
x x
x x
→−∞
→−∞
= −∞
− +
= −
− −
0,5
2
2
2
1 2
1
2
lim lim
x x
x
x x
x x
a
x x
→−∞ →−∞
− − +
− +
= =
0,25
2
1 2
lim 1 1
x
x x
→−∞
= − − + = −
0,25
(
)
2
2
2
lim 2 lim
1 2
1
x x
x
b x x x
x x
x x
→−∞ →−∞
− +
= − + + =
− − + −
0,25
2
2
1
1
lim
2
1 2
1 1
x
x
x x
→−∞
− +
= =
− − + −
0,25
3
1)
(
)
( )
(
)
` . .
BC AB ABCD la h c n
BC SA SA ABCD
⊥
⊥ ⊥
0,25
(
)
BC SAB
BC SB
⇒ ⊥
⇒ ⊥
∆
SBC
⇒
vuông tại B
0,25
(
)
( )
(
)
` . .
CD AD ABCD la h c n
CD SA SA ABCD
⊥
⊥ ⊥
0,25
(
)
CD SAD
CD SD
⇒ ⊥
⇒ ⊥
∆
SCD
⇒
vuông tại D
0,25
2)
(
)
( )
CD SAD
CD AH
AH SAD
⊥
⇒ ⊥
⊂
0,25
( )
CD AH
AH SCD
AH SD
⊥
⇒ ⊥
⊥
0,5
AH SC
⇒ ⊥
0,25
3)
(
)
( )
BC SAB
BC AK
AK SAB
⊥
⇒ ⊥
⊂
0,25
( )
BC AK
AK SBC
AK SB
⊥
⇒ ⊥
⊥
0,25
( )
AK SC
SC AHK
AH SC
⇒ ⊥
⇒ ⊥
⊥
0,25
(
)
(
)
SAC AHK
⇒ ⊥
0,25
4)
Dựng
BI AC
⊥
tại I
(
)
(
)
BI SA SA ABCD
⊥ ⊥
(
)
BI SAC
⇒ ⊥
tại I
0,25
⇒
SI là hình chiếu của SB trên (SAC)
( )
(
)
(
)
, ,
SB SAC SB SI BSI
⇒ = =
0,25
2 2
3
SB SA AB a
= + =
2 2 2
1 1 1 3
2
a
BI
BI BA BC
= + ⇒ =
0,25
( )
(
)
0
1
sin , 30
2
BSI SB SAC BSI= ⇒ = =
0,25
A
D
B C
S
H
K
I
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM
KIỂM TRA GIỮA HỌC KỲ II
TRƯỜNG THPT NGUYỄN CHÍ THANH
Năm học: 2018 - 2019 Môn: TOÁN- Lớp 11
Thời gian: 60 phút (không kể thời gian phát đề)
Bài 1: (5,0 điểm) Tìm các giới hạn sau: 2x2 + 5x + 2 2 x + 5 − 3 2
x − 2x + 5 + 3x −1 1) lim 2) lim 3) lim x→− x3 2 − 2x+4 2
x→2 x − 3x + 2 x→−∞ 2x +1 3 2x − 3x + 5 4) − + − 5) lim →+∞ ( 2 lim 4x 3x 1 2x x ) 2
x→−∞ 3 − x − 2x f(x)
Bài 2: (1,0 điểm) Cho hàm số f (x) 2
= x − x + 2 . Tìm a, b biết a = lim và b = lim f(x) − ax . x ( ) x→−∞ x →−∞
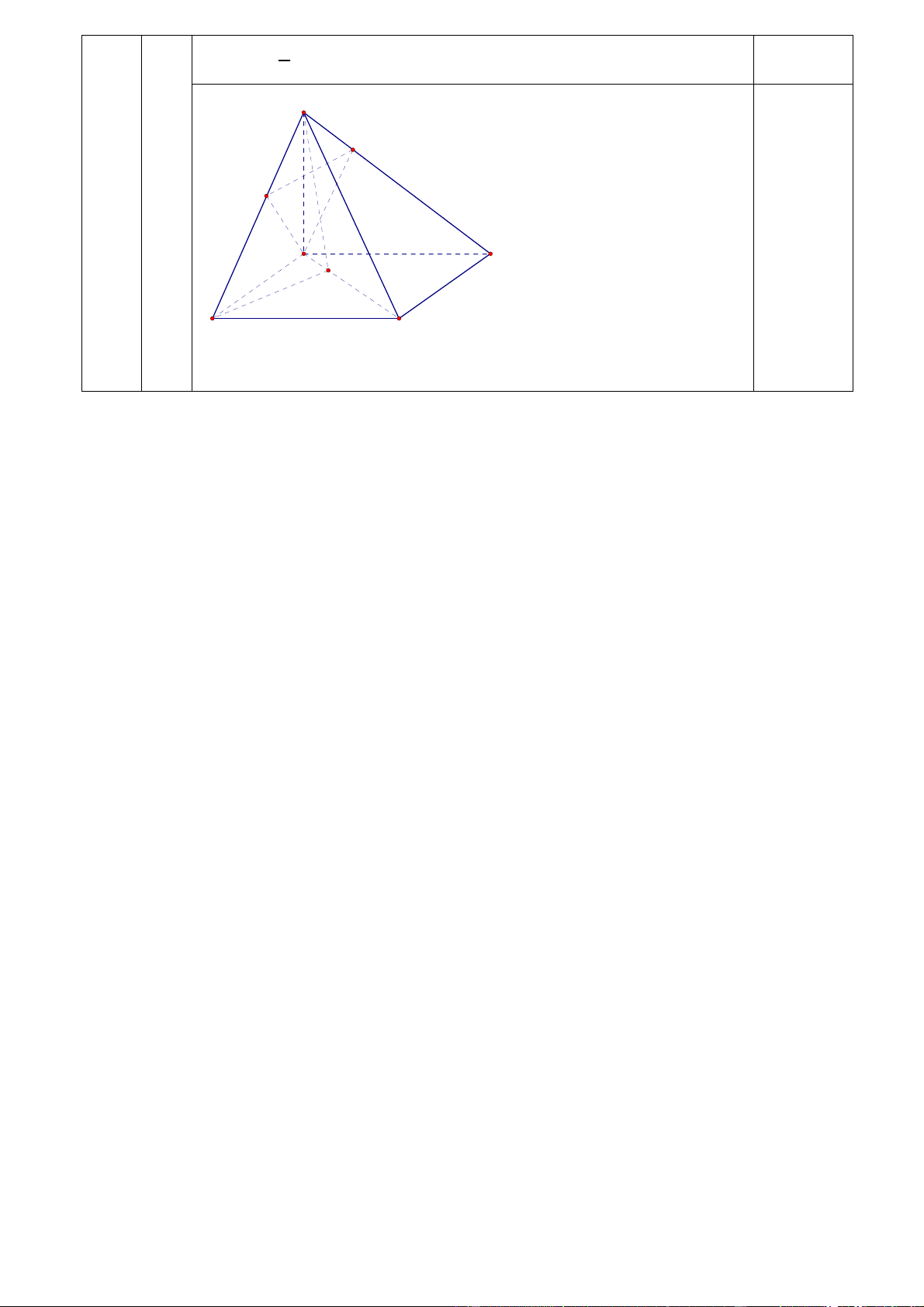
Bài 3:(4,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA ⊥ (ABCD).
1) CMR: các tam giác SBC và SCD là các tam giác vuông.
2) Dựng AH là đường cao của tam giác SAD. Chứng minh: AH ⊥ SC
3) Gọi K là hình chiếu vuông góc của A lên SB. Chứng minh: (SAC) ⊥ (AHK).
4) Cho SA = a 2, AB = a, AD = a 3 . Tính góc hợp bởi SB và (SAC).
––––––––––––––––––––Hết–––––––––––––––––––
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM
KIỂM TRA GIỮA HỌC KỲ II
TRƯỜNG THPT NGUYỄN CHÍ THANH
Năm học: 2018 - 2019 Môn: TOÁN- Lớp 11
Thời gian: 60 phút (không kể thời gian phát đề)
Bài 1: (5,0 điểm) Tìm các giới hạn sau: 2x2 + 5x + 2 2 x + 5 − 3 2
x − 2x + 5 + 3x −1 1) lim 2) lim 3) lim x→− x3 2 − 2x+4 2
x→2 x − 3x + 2 x→−∞ 2x +1 3 2x − 3x + 5 4) − + − 5) lim →+∞ ( 2 lim 4x 3x 1 2x x ) 2
x→−∞ 3 − x − 2x f(x)
Bài 2: (1,0 điểm) Cho hàm số f (x) 2
= x − x + 2 . Tìm a, b biết a = lim và b = lim f(x) − ax . x ( ) x→−∞ x →−∞
Bài 3:(4,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA ⊥ (ABCD).
5) CMR: các tam giác SBC và SCD là các tam giác vuông.
6) Dựng AH là đường cao của tam giác SAD. Chứng minh: AH ⊥ SC
7) Gọi K là hình chiếu vuông góc của A lên SB. Chứng minh: (SAC) ⊥ (AHK).
8) Cho SA = a 2, AB = a, AD = a 3 . Tính góc hợp bởi SB và (SAC).
––––––––––––––––––––Hết–––––––––––––––––––
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
ĐÁP ÁN ĐỀ KIỂM TRA GIỮA HỌC KÌ II – NĂM HỌC 2018 – 2019 MÔN TOÁN LỚP 11 Bài Ý NỘI DUNG ĐIỂM 1 1) 2x2 + 5x + 2 (x +2)(2x+ )1 lim = lim 0,25+0,25 x→− x3 2 − 2x+4 x→ 2
− (x + 2)(x2 −2x +2) 2x +1 3 = lim = − 2
x→−2 x − 2x + 2 10 0,25+0,25 2) 2 x + 5 − 3 2 x − 4 lim = lim 2 0,25
x→2 x − 3x + 2 x→2 ( 2 x −3x + 2)( 2 x + 5 + ) 3 (x −2)(x + 2) = lim x→2 0,25 ( x − 2)(x − ) 1 ( 2 x + 5 + ) 3 x + 2 2 = lim = x→2 ( 0,25+0,25 x − ) 1 ( 2 x + 5 + ) 3 3 3) 2 5 − − + + − 2 x 1 3x 1
x − 2x + 5 + 3x −1 2 x x 0,25 lim = lim x→−∞ 2x +1 x→−∞ 2x +1 2 5 1 − 1− + + 3− 2 x x x = lim 0,5 x→−∞ 1 2 + x = 1 0,25 4) 2 2 − + −
4x −3x +1− 4x = lim 0,25 →+∞ ( 2 lim 4x 3x 1 2x x ) x→+∞ 2
4x −3x +1 + 2x −3x +1 = lim x→+∞ 3 1 0,25 x 4 − + + 2x 2 x x 1 −3+ 3 0,25+0,25 = lim x = − x→+∞ 3 1 4 4 − + + 2 2 x x 5)  3 5    3 2− + 2x − 3x + 5   2 3   lim = lim . x x x    = +∞ 0,5 2  
x→−∞ 3 − x − 2x x→−∞  3 1   − − 2   2    x x   lim x = −∞ x→−∞  3 5  Vì 2 − +  2 3 0,5  lim x x  = −1 x→−∞ 3 1  − − 2 2  x x 2 1 2 − − + 2 x 1 2 x − x + 2 x x 0,25 a = lim = lim x→−∞ x x →−∞ x  1 2    = lim −  1− +  = −1 0,25 2   x→−∞  x x  −x + b = lim
x − x + + x = x→−∞ ( 2 2 2 ) lim x→−∞ 1 2 0,25 −x 1− + − x 2 x x 2 −1+ 1 = lim x = 0,25 x→−∞ 1 2 2 − 1− + −1 2 x x 3 1)
BC ⊥ AB( ABCD la` . h . c n) 0,25
BC ⊥ SA(SA ⊥ (ABCD)) 
⇒ BC ⊥ (SAB) ⇒ BC ⊥ SB 0,25
⇒ ∆SBC vuông tại B
CD ⊥ AD( ABCD la` . h . c n) 0,25
CD ⊥ SA(SA ⊥ (ABCD)) 
⇒ CD ⊥ (SAD) ⇒ CD ⊥ SD 0,25
⇒ ∆SCD vuông tại D 2)
CD ⊥ (SAD)⇒CD ⊥ AH 0,25
AH ⊂ (SAD) CD ⊥ AH
⇒ AH ⊥(SCD) 0,5 AH ⊥ SD   ⇒ AH ⊥ SC 0,25 3)
BC ⊥ (SAB)⇒ BC ⊥ AK 0,25
AK ⊂ (SAB) BC ⊥ AK
⇒ AK ⊥(SBC) 0,25 AK ⊥ SB  
⇒ AK ⊥ SC⇒ SC ⊥(AHK) 0,25 AH ⊥ SC 
⇒ (SAC) ⊥ (AHK ) 0,25 4)
Dựng BI ⊥ AC tại I
BI ⊥ SA (SA ⊥ (ABCD)) 0,25
⇒ BI ⊥ (SAC) tại I
⇒ SI là hình chiếu của SB trên (SAC) ⇒ SB (SAC) ( ) = (SB SI) , , = BSI 0,25 2 2
SB = SA + AB = a 3 1 1 1 a 3 0,25 = + ⇒ BI = 2 2 2 BI BA BC 2 1 sin BSI = ⇒ SB,(SAC) ( ) 0 = BSI = 30 0,25 2 S H K A D I B C