Đề kiểm tra Hình học 11 chương 3 (Quan hệ vuông góc) trường Đông Du – Đăk Lăk

Tài liệu gồm 12 trang với 3 đề kiểm tra 1 tiết Hình học 11 chương 3 của trường THCS – THPT Đông Du – Đăk Lawk. Mỗi đề có 10 câu trắc nghiệm và 1 bài tập tự luận có 4 ý nhỏ.

46 23 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

12 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐAKLAK
TRƯỜNG THCS – THPT ĐÔNG DU
KIỂM TRA ĐỊNH KÌ NĂM HỌC 2016-2017
TOÁN HÌNH HỌC 11 CHƯƠNG III
Thời gian: 45 phút
I PHẦN TRẮC NGHIỆM (5 điểm)
C©u 1 :
Hình chóp tứ giác S.ABCD có đáy ABCD là một hình vuông. Tất cả các cạnh bên và cạnh đáy của
hình chóp đều bằng a . Tích vô hướng là :
A.
B.
C.
D.
0
C©u 2 :
Trong các mệnh đề sau mệnh đề nào sai ?
A.
Cho hai vectơ không cùng phương và và một vectơ trong không gian. Khi đó đồng
phẳng khi và chỉ khi có cặp số m, n duy nhất sao cho .
B.
Ba vectơ đồng phẳng khi và chỉ khi ba vectơ đó cùng có giá thuộc một mặt phẳng.
C.
Ba vectơ đồng phẳng nếu có hai trong ba vectơ đó cùng phương.
D.
Ba vectơ đồng phẳng nếu có một trong ba vectơ đó bằng vectơ .
C©u 3 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I. Biết SA = SC; SB = SD. Trong các mệnh
đề sau, mệnh đề nào sai ?
A.
BD SC⊥
B.
AC SD
⊥
SB AD⊥
()
SI ABCD⊥
C©u 4 :
Cho hình chóp S.ABCD có tất cả các cạnh bên và cạnh đáy đều bằng nhau và ABCD là hình vuông.
Góc giữa đường thẳng SA và mặt phẳng đáy là góc giữa cặp đường thẳng nào?
A.
( )
,SA AB
B.
( )
,SA SC
C.
( )
,SA AC
D.
( )
,SA BD
C©u 5 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, SA vuông góc với mặt phẳng (ABCD).
Chọn khẳng định đúng:
A.
O là hình chiếu vuông góc của S lên mp (ABCD).
B.
A là chiếu vuông góc của C lên mp (SAB).
C.
Trung điểm của AD là chiếu vuông góc của C lên mp (SAD).
D.
O là hình chiếu vuông góc của B lên mp (SAC).
C©u 6 :
Cho hình chóp
S.ABCD
có đáy
ABCD
là hình vuông cạnh
a
, tâm O,
( )
SA ABCD⊥
và
6SA a=
.
Góc giữa đường thẳng SO và mặt phẳng (ABCD) gần bằng ?
A.
0
81
B.
0
74
0
63
0
55
C©u 7 :
Trong các mệnh đề sau, mệnh đề nào có thể SAI ?
A.
Trong không gian, hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song
với nhau.
B.
Trong mặt phẳng, hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song
song với nhau.
.SA SC
 
2
2
a
2
3
2
a
2
a
a
b
c
,,
abc

c ma nb= +

,,abc

,,abc

,,abc

0
2
C.
Trong không gian cho hai đường thẳng song song. Đường thẳng nào vuông góc với đường thẳng này
thì vuông góc với đường thẳng kia.
D.
Trong không gian, hai đường thẳng vuông góc với nhau thì có thể cắt nhau hoặc chéo nhau.
C©u 8 :
Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành. Trong các đẳng thức sau, đẳng thức nào
đúng ?
A.
B.
C.
D.
C©u 9 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a,
0
60BAD =
. SA vuông góc với
mặt phẳng (ABCD), SA=a. Khi đó góc giữa SD và mp (SAC)=?
A.
0
20 42'
≈
B.
0
69 17'≈
0
46 21'≈
0
30 15'≈
C©u 10 :
Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau. Trong các mệnh sau, mệnh đề nào
sai ?
A.
''AC B D⊥
B.
'AA BD⊥
''AB CD⊥
AC BD⊥
PHẦN II TỰ LUẬN (5 điểm)
Cho hình chóp S.ABCD co
SA
⊥
(ABCD), đa
y ABCD la
hı
nh vuông cạnh 2a.
( )
SA ABCD
⊥
,
23
SA a=
.
1 (2đ) Chứng minh các mặt bên của hình chóp là các tam giác vuông.
2.(1đ) Tính góc của SC và mặt phẳng
( )
SAB
.
3.(1đ). Gọi M là trung điểm của SC. Chứng minh
AM BD⊥
.
4. (1đ) Gọi I là trung điểm của AD, mặt phẳng (P) qua I và vuông góc với SD. Xác
định và tính thiết diện của hình chóp cắt bởi mặt phẳng (P).
Hết
SB SD SA SC+=+
   
SA SD SB SC+=+
   
AB AC AD+=
  
0
AB BC CD DA+++=
   
3
phiÕu soi - ®¸p ¸n (Dµnh cho gi¸m kh¶o)
PHÂN TRẮC NGHIỆM
01
{ | } )
02
{ ) } ~
03
{ | ) ~
04
{ | ) ~
05
{ | } )
06
{ ) } ~
07
) | } ~
08
) | } ~
09
) | } ~
10
{ ) } ~
PHẦN TỰ LUẬN
Câu
Đáp án
Điểm
1
2
Câu 2:
Ve
hı
nh
vì
( )
SA ABCD⊥
nên
;SA AB SA AD⊥⊥
,
;SAB SAD∆∆
vuông tại A.
0,5 đ
4
1
2
3
4
BC AB⊥
BC SA⊥
()
BC SAB
⇒⊥
,
BC SB⇒⊥
,
SBC∆
vuông tại B.
DC AD⊥
DC SA⊥
()DC SAD⇒⊥
,
DC SD⇒⊥
,
SDC∆
vuông tại D.
Tính góc của SC và mặt phẳng
(
)
SAB
.
Vì
( )
SA ABCD⊥
nên AC là hình chiếu vuông góc của SC lên mp (ABCD).
Góc của SC và (ABCD) là
SCA
Ta có
2 2; 2 3AC a SA a= =
,
0
3
tan 51
2
SA
SCA SCA
AC
==⇒≈
( )
;BD AC BD SA BD SAC⊥ ⊥⇒ ⊥
,
()AM SAC⊂
BD AM⇒⊥
Dựng được thiết diện IFGH
Tính đúng diện tích
2
3
; 2; .
24
93
.
2 16
a
IH a IF a GH
IF HG
S IH a
= = =
+
= =
0.75d
0.75d
0.5 đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐAKLAK
TRƯỜNG THCS – THPT ĐÔNG DU
KIỂM TRA ĐỊNH KÌ NĂM HỌC 2016-2017
TOÁN HÌNH HỌC 11 CHƯƠNG III
Thời gian: 45 phút
I PHẦN TRẮC NGHIỆM (5 điểm)
C©u 1 :
Trong các mệnh đề sau, mệnh đề nào có thể SAI ?
A.
Trong không gian, hai đường thẳng vuông góc với nhau thì có thể cắt nhau hoặc chéo nhau.
B.
Trong không gian, hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song
với nhau.
C.
Trong mặt phẳng, hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song
song với nhau.
D.
Trong không gian cho hai đường thẳng song song. Đường thẳng nào vuông góc với đường thẳng này
thì vuông góc với đường thẳng kia.
C©u 2 :
Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành. Trong các đẳng thức sau, đẳng thức nào
đúng ?
A.
B.
C.
D.
C©u 3 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a,
0
60BAD =
. SA vuông góc với
mặt phẳng (ABCD), SA=a. Khi đó góc giữa SD và mp (SAC)=?
A.
0
46 21'
≈
B.
0
30 15'≈
0
69 17'≈
0
20 42'≈
C©u 4 :
Trong các mệnh đề sau mệnh đề nào sai ?
A.
Ba vectơ đồng phẳng khi và chỉ khi ba vectơ đó cùng có giá thuộc một mặt phẳng.
B.
Ba vectơ đồng phẳng nếu có một trong ba vectơ đó bằng vectơ .
C.
Ba vectơ đồng phẳng nếu có hai trong ba vectơ đó cùng phương.
D.
Cho hai vectơ không cùng phương và và một vectơ trong không gian. Khi đó đồng
phẳng khi và chỉ khi có cặp số m, n duy nhất sao cho .
C©u 5 :
Cho hình chóp
S.ABCD
có đáy
ABCD
là hình vuông cạnh
a
, tâm O,
( )
SA ABCD
⊥
và
6SA a=
.
Góc giữa đường thẳng SO và mặt phẳng (ABCD) gần bằng ?
A.
0
81
B.
0
55
0
74
0
63
C©u 6 :
Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau. Trong các mệnh sau, mệnh đề nào
sai ?
A.
''AC B D⊥
B.
'AA BD⊥
''
AB CD⊥
AC BD⊥
SB SD SA SC+=+
   
SA SD SB SC+=+
   
AB AC AD+=
  
0AB BC CD DA+++=
   
,,abc

,,abc

0
,,
abc

a
b
c
,,abc

c ma nb= +

2
C©u 7 :
Cho hình chóp S.ABCD có tất cả các cạnh bên và cạnh đáy đều bằng nhau và ABCD là hình vuông.
Góc giữa đường thẳng SA và mặt phẳng đáy là góc giữa cặp đường thẳng nào?
A.
( )
,SA AB
B.
(
)
,SA SC
C.
( )
,SA AC
D.
( )
,SA BD
C©u 8 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I. Biết SA = SC; SB = SD. Trong các mệnh
đề sau, mệnh đề nào sai ?
A.
()SI ABCD⊥
B.
SB AD
⊥
BD SC
⊥
AC SD⊥
C©u 9 :
Hình chóp tứ giác S.ABCD có đáy ABCD là một hình vuông. Tất cả các cạnh bên và cạnh đáy của
hình chóp đều bằng a . Tích vô hướng là :
A.
0
B.
C.
D.
C©u 10 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, SA vuông góc với mặt phẳng (ABCD).
Chọn khẳng định đúng:
A.
Trung điểm của AD là chiếu vuông góc của C lên mp (SAD).
B.
O là hình chiếu vuông góc của S lên mp (ABCD).
C.
A là chiếu vuông góc của C lên mp (SAB).
D.
O là hình chiếu vuông góc của B lên mp (SAC).
II PHẦN TỰ LUÂN (5 điểm)
Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh a. Biết SA
⊥
(ABCD) và SA =a
6
.
1) (2đ) Chứng minh
( ); ( )BC SAB BD SAC⊥⊥
.
2) (1đ) Tính góc giữa SC và (ABCD).
3) (1đ) Gọi AM, AN lần lượt là đường cao của
∆
SAB và
∆
SAD. Chứng minh SC
⊥
MN.
4) (1đ) Gọi E là trung điểm của AB, mặt phẳng (P) qua E và vuông góc với SB.
Xác định và tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P).
HẾT
.SA SC
 
2
2
a
2
3
2
a
2
a
3
phiÕu soi - ®¸p ¸n (Dµnh cho gi¸m kh¶o)
PHẦN TRẮC NGHIỆM
01
{ ) } ~
02
) | } ~
03
{ | } )
04
) | } ~
05
{ | ) ~
06
{ ) } ~
07
{ | ) ~
08
{ ) } ~
09
) | } ~
10
{ | } )
PHẦN TỰ LUẬN
Nội dung
Điểm
4
1
*
()
()
()
()
()
BC AB SAB
SA ABCD
BC SA SAB
BC ABCD
AB SA A
BC SAB
⊥⊂
⊥
⇒ ⊥⊂
⊂
∩=
⇒⊥
*
()BD AC SAC⊥⊂
(gt)
()BD SC SAC
⊥⊂
( Định lý 3 đường vuông góc).
AC SC C∩=
()BD SAC⇒⊥
1,0đ
1,0đ
2
()
SA ABCD⊥
nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD)
(SC;(ABCD)) = (SC;AC) =
SCA
=
ϕ
.
0
6
tan 3 60
2
SA a
AC
a
ϕϕ
= = = ⇒=
0,5đ
0.5đ
3
;
SM SN
SAB SAD SM SN SB SD
SB SD
∆=∆⇒= =⇒ =
//MN BD⇒
( Định lý Ta –
lét)
Mà
() ()BD SAC MN SAC MN SC⊥ ⇒⊥ ⇒⊥
0,5đ
0,5đ
4
Dựng được thiết diện là EFGH.
2
42 13
;; .
14 14
27 42
.
2 392
EH a EF a GH a
FE HG
S EH a
= = =
+
= =
0,5đ
0,5đ
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐAKLAK
TRƯỜNG THCS – THPT ĐÔNG DU
KIỂM TRA ĐỊNH KÌ NĂM HỌC 2016-2017
TOÁN HÌNH HỌC 11 CHƯƠNG III
Thời gian: 45 phút
I PHẦN TRẮC NGHIỆM (5 điểm)
C©u 1 :
Hình chóp tứ giác S.ABCD có đáy ABCD là một hình vuông. Tất cả các cạnh bên và cạnh đáy của
hình chóp đều bằng a . Tích vô hướng là :
A.
B.
C.
D.
0
C©u 2 :
Trong các mệnh đề sau mệnh đề nào sai ?
A.
Cho hai vectơ không cùng phương và và một vectơ trong không gian. Khi đó đồng
phẳng khi và chỉ khi có cặp số m, n duy nhất sao cho .
B.
Ba vectơ đồng phẳng khi và chỉ khi ba vectơ đó cùng có giá thuộc một mặt phẳng.
C.
Ba vectơ đồng phẳng nếu có hai trong ba vectơ đó cùng phương.
D.
Ba vectơ đồng phẳng nếu có một trong ba vectơ đó bằng vectơ .
C©u 3 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I. Biết SA = SC; SB = SD. Trong các mệnh
đề sau, mệnh đề nào sai ?
A.
BD SC⊥
B.
AC SD
⊥
SB AD⊥
()
SI ABCD⊥
C©u 4 :
Cho hình chóp S.ABCD có tất cả các cạnh bên và cạnh đáy đều bằng nhau và ABCD là hình vuông.
Góc giữa đường thẳng SA và mặt phẳng đáy là góc giữa cặp đường thẳng nào?
A.
( )
,SA AB
B.
( )
,SA SC
C.
( )
,SA AC
D.
( )
,SA BD
C©u 5 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, SA vuông góc với mặt phẳng (ABCD).
Chọn khẳng định đúng:
A.
O là hình chiếu vuông góc của S lên mp (ABCD).
B.
A là chiếu vuông góc của C lên mp (SAB).
C.
Trung điểm của AD là chiếu vuông góc của C lên mp (SAD).
D.
O là hình chiếu vuông góc của B lên mp (SAC).
C©u 6 :
Cho hình chóp
S.ABCD
có đáy
ABCD
là hình vuông cạnh
a
, tâm O,
( )
SA ABCD⊥
và
6SA a=
.
Góc giữa đường thẳng SO và mặt phẳng (ABCD) gần bằng ?
A.
0
81
B.
0
74
0
63
0
55
C©u 7 :
Trong các mệnh đề sau, mệnh đề nào có thể SAI ?
A.
Trong không gian, hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song
với nhau.
B.
Trong mặt phẳng, hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song
song với nhau.
.SA SC
 
2
2
a
2
3
2
a
2
a
a
b
c
,,
abc

c ma nb= +

,,abc

,,abc

,,abc

0
2
C.
Trong không gian cho hai đường thẳng song song. Đường thẳng nào vuông góc với đường thẳng này
thì vuông góc với đường thẳng kia.
D.
Trong không gian, hai đường thẳng vuông góc với nhau thì có thể cắt nhau hoặc chéo nhau.
C©u 8 :
Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành. Trong các đẳng thức sau, đẳng thức nào
đúng ?
A.
B.
C.
D.
C©u 9 :
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a,
0
60BAD =
. SA vuông góc với
mặt phẳng (ABCD), SA=a. Khi đó góc giữa SD và mp (SAC)=?
A.
0
20 42'
≈
B.
0
69 17'≈
0
46 21'≈
0
30 15'≈
C©u 10 :
Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau. Trong các mệnh sau, mệnh đề nào
sai ?
A.
''AC B D⊥
B.
'AA BD⊥
''AB CD⊥
AC BD⊥
PHẦN II TỰ LUẬN (5 điểm)
Cho hình chóp S.ABCD co
SA
⊥
(ABCD), đa
y ABCD la
hı
nh vuông cạnh 2a.
( )
SA ABCD
⊥
,
23
SA a=
.
1 (2đ) Chứng minh các mặt bên của hình chóp là các tam giác vuông.
2.(1đ) Tính góc của SC và mặt phẳng
( )
SAB
.
3.(1đ). Gọi M là trung điểm của SC. Chứng minh
AM BD⊥
.
4. (1đ) Gọi I là trung điểm của AD, mặt phẳng (P) qua I và vuông góc với SD. Xác
định và tính thiết diện của hình chóp cắt bởi mặt phẳng (P).
Hết
SB SD SA SC+=+
   
SA SD SB SC+=+
   
AB AC AD+=
  
0
AB BC CD DA+++=
   
3
phiÕu soi - ®¸p ¸n (Dµnh cho gi¸m kh¶o)
PHÂN TRẮC NGHIỆM
01
{ | } )
02
{ ) } ~
03
{ | ) ~
04
{ | ) ~
05
{ | } )
06
{ ) } ~
07
) | } ~
08
) | } ~
09
) | } ~
10
{ ) } ~
PHẦN TỰ LUẬN
Câu
Đáp án
Điểm
1
2
Câu 2:
Ve
hı
nh
vì
( )
SA ABCD⊥
nên
;SA AB SA AD⊥⊥
,
;SAB SAD∆∆
vuông tại A.
0,5 đ
4
1
2
3
4
BC AB⊥
BC SA⊥
()
BC SAB
⇒⊥
,
BC SB⇒⊥
,
SBC∆
vuông tại B.
DC AD⊥
DC SA⊥
()DC SAD⇒⊥
,
DC SD⇒⊥
,
SDC∆
vuông tại D.
Tính góc của SC và mặt phẳng
(
)
SAB
.
Vì
( )
BC SAB⊥
nên SB là hình chiếu vuông góc của SC lên mp (SAB).
Góc của SC và (SBC) là
BSC
( )
;BD AC BD SA BD SAC⊥ ⊥⇒ ⊥
,
()AM SAC
⊂
BD AM⇒⊥
Dựng được thiết diện IFGH
Tính đúng diện tích
2
3
; 2; .
24
93
.
2 16
a
IH a IF a GH
IF HG
S IH a
= = =
+
= =
0.75d
0.75d
0.5 đ
0,5đ
0,5đ
0,5đ
0,5đ
0,5đ
| 1/12
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐAKLAK
KIỂM TRA ĐỊNH KÌ NĂM HỌC 2016-2017
TRƯỜNG THCS – THPT ĐÔNG DU
TOÁN HÌNH HỌC 11 CHƯƠNG III Thời gian: 45 phút
I PHẦN TRẮC NGHIỆM (5 điểm)
C©u 1 : Hình chóp tứ giác S.ABCD có đáy ABCD là một hình vuông. Tất cả các cạnh bên và cạnh đáy của  
hình chóp đều bằng a . Tích vô hướng SA. SC là : 2 a 2 a 3 A. 2 B. C. a D. 0 2 2
C©u 2 : Trong các mệnh đề sau mệnh đề nào sai ?      
Cho hai vectơ không cùng phương a và b và một vectơ c trong không gian. Khi đó a,b,c đồng A.   
phẳng khi và chỉ khi có cặp số m, n duy nhất sao cho c = ma + nb .   
B. Ba vectơ a ,b,c đồng phẳng khi và chỉ khi ba vectơ đó cùng có giá thuộc một mặt phẳng.   
C. Ba vectơ a ,b,c đồng phẳng nếu có hai trong ba vectơ đó cùng phương.    
D. Ba vectơ a ,b,c đồng phẳng nếu có một trong ba vectơ đó bằng vectơ 0 .
C©u 3 : Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I. Biết SA = SC; SB = SD. Trong các mệnh
đề sau, mệnh đề nào sai ?
A. BD ⊥ SC
B. AC ⊥ SD
C. SB ⊥ AD
D. SI ⊥ ( ABC ) D
C©u 4 : Cho hình chóp S.ABCD có tất cả các cạnh bên và cạnh đáy đều bằng nhau và ABCD là hình vuông.
Góc giữa đường thẳng SA và mặt phẳng đáy là góc giữa cặp đường thẳng nào? A. ( S , A AB) B. ( , SA SC ) C. ( S , A AC ) D. ( S , A BD)
C©u 5 : Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, SA vuông góc với mặt phẳng (ABCD).
Chọn khẳng định đúng:
A. O là hình chiếu vuông góc của S lên mp (ABCD).
B. A là chiếu vuông góc của C lên mp (SAB).
C. Trung điểm của AD là chiếu vuông góc của C lên mp (SAD).
D. O là hình chiếu vuông góc của B lên mp (SAC).
C©u 6 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tâm O, SA ⊥ (ABCD) và SA = a 6 .
Góc giữa đường thẳng SO và mặt phẳng (ABCD) gần bằng ? A. 0 81 B. 0 74 C. 0 63 D. 0 55
C©u 7 : Trong các mệnh đề sau, mệnh đề nào có thể SAI ?
A. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
B. Trong mặt phẳng, hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau. 1
C. Trong không gian cho hai đường thẳng song song. Đường thẳng nào vuông góc với đường thẳng này
thì vuông góc với đường thẳng kia.
D. Trong không gian, hai đường thẳng vuông góc với nhau thì có thể cắt nhau hoặc chéo nhau.
C©u 8 : Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành. Trong các đẳng thức sau, đẳng thức nào đúng ?
   
   
A. SB + SD = SA + SC
B. SA + SD = SB + SC
  
   
C. AB + AC = AD
D. AB + BC + CD + DA = 0
C©u 9 : Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a,  0
BAD = 60 . SA vuông góc với
mặt phẳng (ABCD), SA=a. Khi đó góc giữa SD và mp (SAC)=? A. 0 ≈ 20 42' B. 0 ≈ 69 17 ' C. 0 ≈ 46 21' D. 0 ≈ 30 15'
C©u 10 : Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau. Trong các mệnh sau, mệnh đề nào sai ?
A. AC ⊥ B ' D'
B. AA' ⊥ BD
C. AB ' ⊥ CD'
D. AC ⊥ BD
PHẦN II TỰ LUẬN (5 điểm)
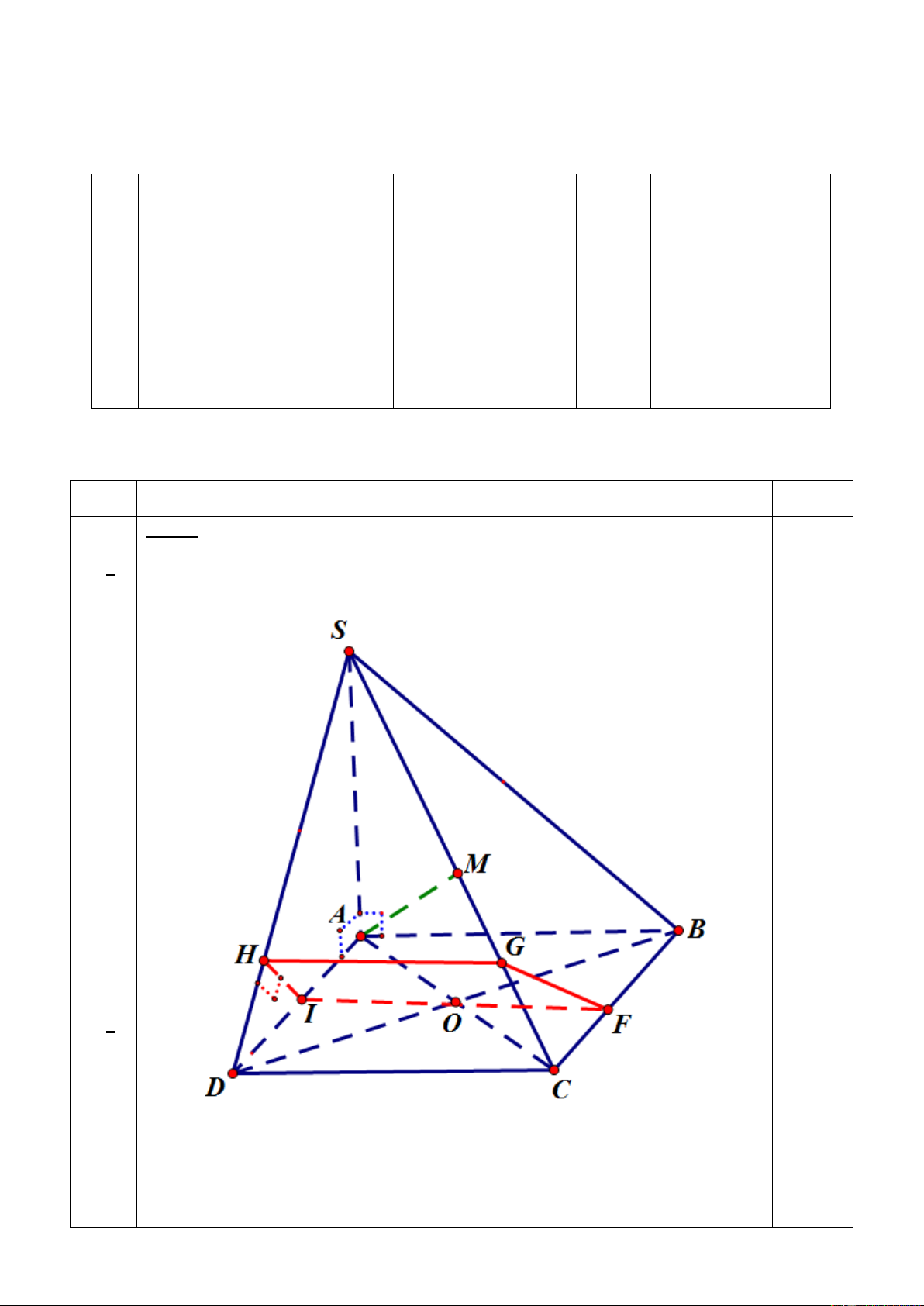
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hı̀nh vuông cạnh 2a.
SA ⊥ ( ABCD) , SA = 2a 3 .
1 (2đ) Chứng minh các mặt bên của hình chóp là các tam giác vuông.
2.(1đ) Tính góc của SC và mặt phẳng (SAB).
3.(1đ). Gọi M là trung điểm của SC. Chứng minh AM ⊥ BD .
4. (1đ) Gọi I là trung điểm của AD, mặt phẳng (P) qua I và vuông góc với SD. Xác
định và tính thiết diện của hình chóp cắt bởi mặt phẳng (P). Hết 2
phiÕu soi - ®¸p ¸n (Dµnh cho gi¸m kh¶o) PHÂN TRẮC NGHIỆM 01 { | } ) 02 { ) } ~ 03 { | ) ~ 04 { | ) ~ 05 { | } ) 06 { ) } ~ 07 ) | } ~ 08 ) | } ~ 09 ) | } ~ 10 { ) } ~ PHẦN TỰ LUẬN Câu Đáp án Điểm Câu 2: 1 Vẽ hı̀nh 2
vì SA ⊥ ( ABCD) nên SA ⊥ A ;
B SA ⊥ AD , S ∆ A ; B S
∆ AD vuông tại A. 0,5 đ 3 1 BC ⊥ AB BC ⊥ SA 0.75d
⇒ BC ⊥ (SAB) ,
⇒ BC ⊥ SB , S ∆ BC vuông tại B. DC ⊥ AD DC ⊥ SA ⇒ ⊥ 0.75d DC (SAD) , ∆
⇒ DC ⊥ SD , SDC vuông tại D. 2
Tính góc của SC và mặt phẳng (SAB) . 0.5 đ
Vì SA ⊥ ( ABCD) nên AC là hình chiếu vuông góc của SC lên mp (ABCD).
Góc của SC và (ABCD) là SCA SA 3 0,5đ = = ⇒ 
Ta có AC = 2a 2; SA = 2a 3 , 0 tan SCA SCA ≈ 51 AC 2 0,5đ
BD ⊥ AC; BD ⊥ SA ⇒ BD ⊥ (SAC ) , AM ⊂ (SAC) 3 0,5đ ⇒ ⊥ BD AM 0,5đ
Dựng được thiết diện IFGH Tính đúng diệ 4 n tích 3 a IH =
a; IF = 2a;GH = . 2 4 IF + HG 9 3 0,5đ 2 S = .IH = a 2 16 4
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐAKLAK
KIỂM TRA ĐỊNH KÌ NĂM HỌC 2016-2017
TRƯỜNG THCS – THPT ĐÔNG DU
TOÁN HÌNH HỌC 11 CHƯƠNG III Thời gian: 45 phút
I PHẦN TRẮC NGHIỆM (5 điểm)
C©u 1 : Trong các mệnh đề sau, mệnh đề nào có thể SAI ?
A. Trong không gian, hai đường thẳng vuông góc với nhau thì có thể cắt nhau hoặc chéo nhau.
B. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
C. Trong mặt phẳng, hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.
D. Trong không gian cho hai đường thẳng song song. Đường thẳng nào vuông góc với đường thẳng này
thì vuông góc với đường thẳng kia.
C©u 2 : Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành. Trong các đẳng thức sau, đẳng thức nào đúng ?
   
   
A. SB + SD = SA + SC
B. SA + SD = SB + SC
  
   
C. AB + AC = AD
D. AB + BC + CD + DA = 0
C©u 3 : Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a,  0
BAD = 60 . SA vuông góc với
mặt phẳng (ABCD), SA=a. Khi đó góc giữa SD và mp (SAC)=? A. 0 ≈ 46 21' B. 0 ≈ 30 15' C. 0 ≈ 69 17 ' D. 0 ≈ 20 42'
C©u 4 : Trong các mệnh đề sau mệnh đề nào sai ?   
A. Ba vectơ a ,b,c đồng phẳng khi và chỉ khi ba vectơ đó cùng có giá thuộc một mặt phẳng.    
B. Ba vectơ a ,b,c đồng phẳng nếu có một trong ba vectơ đó bằng vectơ 0 .   
C. Ba vectơ a ,b,c đồng phẳng nếu có hai trong ba vectơ đó cùng phương.      
Cho hai vectơ không cùng phương a và b và một vectơ c trong không gian. Khi đó a,b,c đồng D.   
phẳng khi và chỉ khi có cặp số m, n duy nhất sao cho c = ma + nb .
C©u 5 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tâm O, SA ⊥ (ABCD) và SA = a 6 .
Góc giữa đường thẳng SO và mặt phẳng (ABCD) gần bằng ? A. 0 81 B. 0 55 C. 0 74 D. 0 63
C©u 6 : Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau. Trong các mệnh sau, mệnh đề nào sai ?
A. AC ⊥ B ' D'
B. AA' ⊥ BD
C. AB ' ⊥ CD'
D. AC ⊥ BD 1
C©u 7 : Cho hình chóp S.ABCD có tất cả các cạnh bên và cạnh đáy đều bằng nhau và ABCD là hình vuông.
Góc giữa đường thẳng SA và mặt phẳng đáy là góc giữa cặp đường thẳng nào? A. ( S , A AB) B. ( , SA SC ) C. ( S , A AC ) D. ( S , A BD)
C©u 8 : Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I. Biết SA = SC; SB = SD. Trong các mệnh
đề sau, mệnh đề nào sai ?
A. SI ⊥ ( ABC ) D
B. SB ⊥ AD
C. BD ⊥ SC
D. AC ⊥ SD
C©u 9 : Hình chóp tứ giác S.ABCD có đáy ABCD là một hình vuông. Tất cả các cạnh bên và cạnh đáy của  
hình chóp đều bằng a . Tích vô hướng SA. SC là : 2 a 2 a 3 A. 0 B. C. 2 D. a 2 2
C©u 10 : Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, SA vuông góc với mặt phẳng (ABCD).
Chọn khẳng định đúng:
A. Trung điểm của AD là chiếu vuông góc của C lên mp (SAD).
B. O là hình chiếu vuông góc của S lên mp (ABCD).
C. A là chiếu vuông góc của C lên mp (SAB).
D. O là hình chiếu vuông góc của B lên mp (SAC).
II PHẦN TỰ LUÂN (5 điểm)
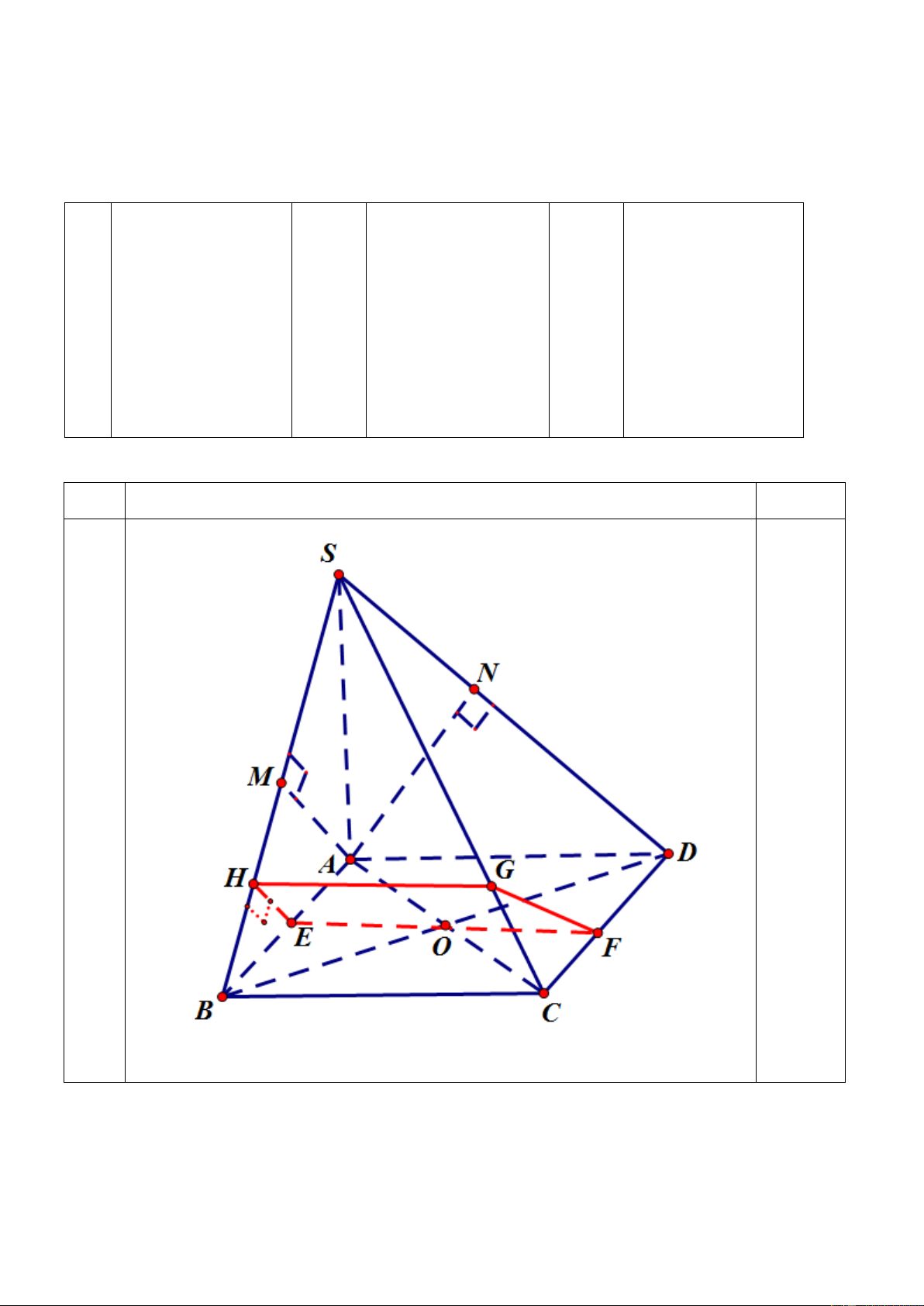
Cho hình chóp S.ABCD có đáy là hình vuông tâm O cạnh a. Biết SA ⊥ (ABCD) và SA =a 6 .
1) (2đ) Chứng minh BC ⊥ (SAB); BD ⊥ (SAC) .
2) (1đ) Tính góc giữa SC và (ABCD).
3) (1đ) Gọi AM, AN lần lượt là đường cao của ∆ SAB và ∆ SAD. Chứng minh SC ⊥ MN.
4) (1đ) Gọi E là trung điểm của AB, mặt phẳng (P) qua E và vuông góc với SB.
Xác định và tính diện tích thiết diện của hình chóp cắt bởi mặt phẳng (P). HẾT 2
phiÕu soi - ®¸p ¸n (Dµnh cho gi¸m kh¶o) PHẦN TRẮC NGHIỆM 01 { ) } ~ 02 ) | } ~ 03 { | } ) 04 ) | } ~ 05 { | ) ~ 06 { ) } ~ 07 { | ) ~ 08 { ) } ~ 09 ) | } ~ 10 { | } ) PHẦN TỰ LUẬN Nội dung Điểm 3 1
BC ⊥ AB ⊂ (SAB)
SA ⊥ ( ABCD) 
 ⇒ BC ⊥ SA ⊂ (SAB)
* BC ⊂ ( ABCD)
AB ∩ SA = A ⇒ BC ⊥ (SAB) 1,0đ
* BD ⊥ AC ⊂ (SAC) (gt)
BD ⊥ SC ⊂ (SAC) ( Định lý 3 đường vuông góc). 1,0đ
AC ∩ SC = C
⇒ BD ⊥ (SAC) 2
SA ⊥ ( ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD) 0,5đ 
(SC;(ABCD)) = (SC;AC) = SCA = ϕ . SA a 6 0 tan ϕ = = = 3 ⇒ ϕ = 60 0.5đ AC a 2 3 SM SN 0,5đ SA ∆ B = SA
∆ D ⇒ SM = SN; SB = SD ⇒ =
⇒ MN // BD ( Định lý Ta – SB SD lét) 0,5đ
Mà BD ⊥ (SAC) ⇒ MN ⊥ (SAC) ⇒ MN ⊥ SC 4
Dựng được thiết diện là EFGH. 0,5đ 42 13 EH = ; a EF = ; a GH = . a 14 14 0,5đ FE + HG 27 42 2 S = .EH = a 2 392 4
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐAKLAK
KIỂM TRA ĐỊNH KÌ NĂM HỌC 2016-2017
TRƯỜNG THCS – THPT ĐÔNG DU
TOÁN HÌNH HỌC 11 CHƯƠNG III Thời gian: 45 phút
I PHẦN TRẮC NGHIỆM (5 điểm)
C©u 1 : Hình chóp tứ giác S.ABCD có đáy ABCD là một hình vuông. Tất cả các cạnh bên và cạnh đáy của  
hình chóp đều bằng a . Tích vô hướng SA. SC là : 2 a 2 a 3 A. 2 B. C. a D. 0 2 2
C©u 2 : Trong các mệnh đề sau mệnh đề nào sai ?      
Cho hai vectơ không cùng phương a và b và một vectơ c trong không gian. Khi đó a,b,c đồng A.   
phẳng khi và chỉ khi có cặp số m, n duy nhất sao cho c = ma + nb .   
B. Ba vectơ a ,b,c đồng phẳng khi và chỉ khi ba vectơ đó cùng có giá thuộc một mặt phẳng.   
C. Ba vectơ a ,b,c đồng phẳng nếu có hai trong ba vectơ đó cùng phương.    
D. Ba vectơ a ,b,c đồng phẳng nếu có một trong ba vectơ đó bằng vectơ 0 .
C©u 3 : Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I. Biết SA = SC; SB = SD. Trong các mệnh
đề sau, mệnh đề nào sai ?
A. BD ⊥ SC
B. AC ⊥ SD
C. SB ⊥ AD
D. SI ⊥ ( ABC ) D
C©u 4 : Cho hình chóp S.ABCD có tất cả các cạnh bên và cạnh đáy đều bằng nhau và ABCD là hình vuông.
Góc giữa đường thẳng SA và mặt phẳng đáy là góc giữa cặp đường thẳng nào? A. ( S , A AB) B. ( , SA SC ) C. ( S , A AC ) D. ( S , A BD)
C©u 5 : Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, SA vuông góc với mặt phẳng (ABCD).
Chọn khẳng định đúng:
A. O là hình chiếu vuông góc của S lên mp (ABCD).
B. A là chiếu vuông góc của C lên mp (SAB).
C. Trung điểm của AD là chiếu vuông góc của C lên mp (SAD).
D. O là hình chiếu vuông góc của B lên mp (SAC).
C©u 6 : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tâm O, SA ⊥ (ABCD) và SA = a 6 .
Góc giữa đường thẳng SO và mặt phẳng (ABCD) gần bằng ? A. 0 81 B. 0 74 C. 0 63 D. 0 55
C©u 7 : Trong các mệnh đề sau, mệnh đề nào có thể SAI ?
A. Trong không gian, hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.
B. Trong mặt phẳng, hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau. 1
C. Trong không gian cho hai đường thẳng song song. Đường thẳng nào vuông góc với đường thẳng này
thì vuông góc với đường thẳng kia.
D. Trong không gian, hai đường thẳng vuông góc với nhau thì có thể cắt nhau hoặc chéo nhau.
C©u 8 : Cho hình chóp S.ABCD, có đáy ABCD là hình bình hành. Trong các đẳng thức sau, đẳng thức nào đúng ?
   
   
A. SB + SD = SA + SC
B. SA + SD = SB + SC
  
   
C. AB + AC = AD
D. AB + BC + CD + DA = 0
C©u 9 : Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a,  0
BAD = 60 . SA vuông góc với
mặt phẳng (ABCD), SA=a. Khi đó góc giữa SD và mp (SAC)=? A. 0 ≈ 20 42' B. 0 ≈ 69 17 ' C. 0 ≈ 46 21' D. 0 ≈ 30 15'
C©u 10 : Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau. Trong các mệnh sau, mệnh đề nào sai ?
A. AC ⊥ B ' D'
B. AA' ⊥ BD
C. AB ' ⊥ CD'
D. AC ⊥ BD
PHẦN II TỰ LUẬN (5 điểm)
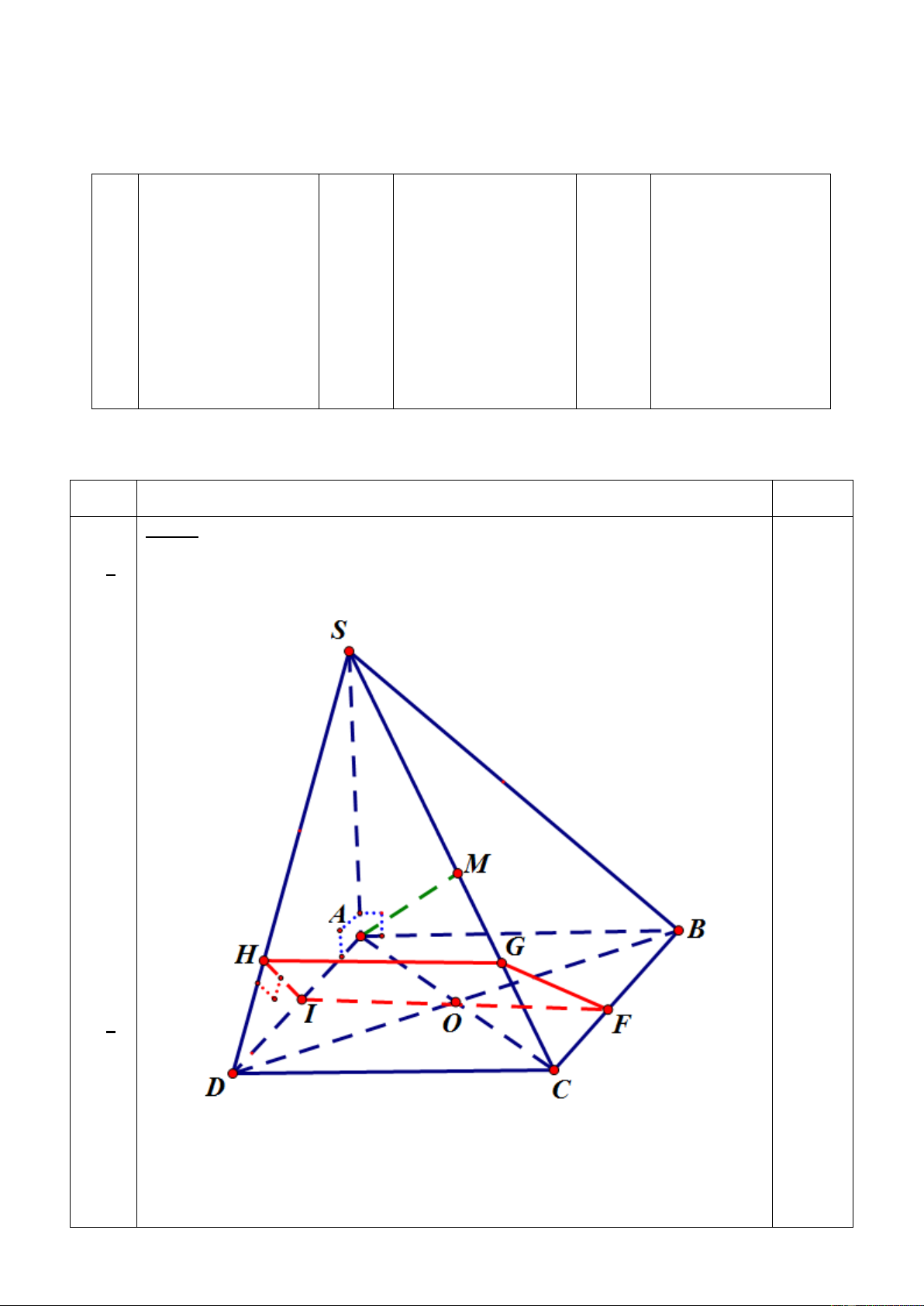
Cho hình chóp S.ABCD có SA ⊥ (ABCD), đáy ABCD là hı̀nh vuông cạnh 2a.
SA ⊥ ( ABCD) , SA = 2a 3 .
1 (2đ) Chứng minh các mặt bên của hình chóp là các tam giác vuông.
2.(1đ) Tính góc của SC và mặt phẳng (SAB).
3.(1đ). Gọi M là trung điểm của SC. Chứng minh AM ⊥ BD .
4. (1đ) Gọi I là trung điểm của AD, mặt phẳng (P) qua I và vuông góc với SD. Xác
định và tính thiết diện của hình chóp cắt bởi mặt phẳng (P). Hết 2
phiÕu soi - ®¸p ¸n (Dµnh cho gi¸m kh¶o) PHÂN TRẮC NGHIỆM 01 { | } ) 02 { ) } ~ 03 { | ) ~ 04 { | ) ~ 05 { | } ) 06 { ) } ~ 07 ) | } ~ 08 ) | } ~ 09 ) | } ~ 10 { ) } ~ PHẦN TỰ LUẬN Câu Đáp án Điểm Câu 2: 1 Vẽ hı̀nh 2
vì SA ⊥ ( ABCD) nên SA ⊥ A ;
B SA ⊥ AD , S ∆ A ; B S
∆ AD vuông tại A. 0,5 đ 3 1 BC ⊥ AB BC ⊥ SA 0.75d
⇒ BC ⊥ (SAB) ,
⇒ BC ⊥ SB , S ∆ BC vuông tại B. DC ⊥ AD DC ⊥ SA ⇒ ⊥ 0.75d DC (SAD) , ∆
⇒ DC ⊥ SD , SDC vuông tại D. 2
Tính góc của SC và mặt phẳng (SAB) . 0.5 đ
Vì BC ⊥ (SAB) nên SB là hình chiếu vuông góc của SC lên mp (SAB).
Góc của SC và (SBC) là BSC 0,5đ 0,5đ 3 0,5đ
BD ⊥ AC; BD ⊥ SA ⇒ BD ⊥ (SAC ) , AM ⊂ (SAC) 0,5đ ⇒ BD ⊥ AM 4
Dựng được thiết diện IFGH Tính đúng diệ n tích 3 a IH =
a; IF = 2a;GH = . 0,5đ 2 4 IF + HG 9 3 2 S = .IH = a 2 16 4
Document Outline

  • De kiem tra chuong 3 50 TL 50 TN hay va kho de 2
  • De KT chuong 3 HH 11 50 TN 50 TL
  • De KT Hinh hoc 11 chuong 3 50 TN 50 TL de 2