Đề kiểm tra HK1 Toán 11 năm 2019 – 2020 trường THPT Thị xã Quảng Trị

SỞ GD-ĐT QUẢNG TRỊ ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2019-2020
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ Môn: Toán - Lớp: 11
Thời gian làm bài: 90 phút, không kể thời gian giao đề Đề KT chính thức (Đề có 01 trang) Mã đề: 01
Câu 1 (2,5 điểm). Giải các phương trình sau:
a) 2𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 − 1 = 0
b) 3𝑠𝑠𝑠𝑠𝑠𝑠2𝑠𝑠 − 4𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 + 𝑠𝑠𝑠𝑠𝑠𝑠2𝑠𝑠 = 0
c) 𝑠𝑠𝑠𝑠𝑠𝑠3 �𝑠𝑠 + 𝜋𝜋� = √2𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 4
Câu 2 (1,5 điểm)
a) Tìm hệ số 𝑠𝑠6 trong khai triển (2𝑠𝑠 + 1)8 thành đa thức.
b) Tìm số tự nhiên 𝑠𝑠 > 5 trong khai triển (𝑠𝑠 + 1)𝑛𝑛 thành đa thức biến 𝑠𝑠, có hệ số 𝑠𝑠6 bằng 4 lần 2 hệ số 𝑠𝑠4.
Câu 3 (2,0 điểm). Một hộp có chứa 7 viên bi xanh được đánh số từ 1 đến 7 và 5 viên bi đỏ được đánh
số từ 8 đến 12. Chọn ngẫu nhiên hai viên bi.
a) Tính xác suất để chọn được 2 viên bi cùng màu.
b) Tính xác suất để chọn được hai viên bi khác màu và tổng 2 số ghi trên hai viên bi là số chẵn.
Câu 4 (2,0 điểm). Trong mặt phẳng (Oxy) cho điểm A( 2;-1) và đường tròn (C) có tâm I(1;-2) bán kính R=3.
a) Tìm tọa độ điểm 𝐴𝐴′ là ảnh của điểm A qua phép tịnh tiến 𝑇𝑇→ với → (3; −2) 𝑢𝑢 𝑢𝑢
b) Viết phương trình đường tròn ( C’) là ảnh của đường tròn ( C) qua phép đồng dạng có được bằng
cách thực hiện liên tiếp phép đối xứng trục Ox và phép vị tự tâm O tỉ số 𝑘𝑘 = −3.
Câu 5 (2,0 điểm) . Cho hình chóp 𝑆𝑆. 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 có đáy 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 là hình bình hành. Gọi M, N lần lượt trung
điểm 𝐴𝐴𝐴𝐴 và 𝑆𝑆𝐴𝐴 .
a) Tìm giao tuyến (𝑆𝑆𝐴𝐴𝐴𝐴) ⋂(𝑆𝑆𝐴𝐴𝐴𝐴)𝑣𝑣à (𝑆𝑆𝐴𝐴𝐴𝐴) ⋂(𝑆𝑆𝐴𝐴𝐴𝐴). 𝐴𝐴𝐴𝐴
b) Tìm giao điểm I của 𝐴𝐴𝐴𝐴 với mặt phẳng (𝑆𝑆𝐴𝐴𝑆𝑆)và tính 𝐴𝐴𝐴𝐴
----------------- HẾT -----------------
Học sinh không được sử dụng tài liệu. CBCT không giải thích gì thêm.
Họ và tên học sinh: …………………………………… Lớp: …………. Số báo danh: ………….
Chữ ký của CBCT: ……………………………………
SỞ GD-ĐT QUẢNG TRỊ ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2019-2020
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ Môn: Toán - Lớp: 11
Thời gian làm bài: 90 phút, không kể thời gian giao đề Đề KT chính thức (Đề có 01 trang) Mã đề: 02
Câu 1 (2,5 điểm). Giải các phương trình sau:
a) 2𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 − √3 = 0
b) 𝑠𝑠𝑠𝑠𝑠𝑠2𝑠𝑠 − 3𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 + 2𝑠𝑠𝑠𝑠𝑠𝑠2𝑠𝑠 = 0
c) √2𝑠𝑠𝑠𝑠𝑠𝑠3 �𝑠𝑠 − 𝜋𝜋� = 2𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 4
Câu 2 (1,5 điểm)
a) Tìm hệ số 𝑠𝑠7 trong khai triển (3𝑠𝑠 + 1)11 thành đa thức.
b) Tìm số tự nhiên 𝑠𝑠 > 5 trong khai triển (𝑠𝑠 + 1)𝑛𝑛 thành đa thức biến 𝑠𝑠, có hệ số 𝑠𝑠7 bằng 9 lần 3 hệ số 𝑠𝑠5.
Câu 3 (2,0 điểm). Một hộp có chứa 9 viên bi xanh được đánh số từ 1 đến 9 và 5 viên bi đỏ được đánh
số từ 10 đến 14. Chọn ngẫu nhiên hai viên bi.
a) Tính xác suất để chọn được 2 viên bi cùng màu.
b) Tính xác suất để chọn được hai viên bi khác màu và tổng 2 số ghi trên hai viên bi là số lẻ.
Câu 4 (2,0 điểm). Trong mặt phẳng (Oxy) cho điểm A( -2;3) và đường tròn (C) có tâm I(3;-1) bán kính R=4.
a) Tìm tọa độ điểm 𝐴𝐴′ là ảnh của điểm A qua phép tịnh tiến 𝑇𝑇→ với → (4; −1) 𝑢𝑢 𝑢𝑢
b) Viết phương trình đường tròn ( C’) là ảnh của đường tròn ( C) qua phép đồng dạng có được bằng
cách thực hiện liên tiếp phép đối xứng trục Oy và phép vị tự tâm O tỉ số 𝑘𝑘 = −2.
Câu 5 (2,0 điểm). Cho hình chóp 𝑆𝑆. 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 có đáy 𝐴𝐴𝐴𝐴𝐴𝐴𝐴𝐴 là hình bình hành. Gọi M, N lần lượt trung
điểm 𝑆𝑆𝐴𝐴 và 𝐴𝐴𝐴𝐴 .
a) Tìm giao tuyến (𝑆𝑆𝐴𝐴𝐴𝐴) ⋂(𝑆𝑆𝐴𝐴𝐴𝐴)𝑣𝑣à (𝑆𝑆𝐴𝐴𝐴𝐴) ⋂(𝑆𝑆𝐴𝐴𝐴𝐴). 𝐴𝐴𝐴𝐴
b) Tìm giao điểm I của 𝐴𝐴𝑆𝑆 với mặt phẳng (𝑆𝑆𝐴𝐴𝐴𝐴)và tính 𝐴𝐴𝐴𝐴
----------------- HẾT -----------------
Học sinh không được sử dụng tài liệu. CBCT không giải thích gì thêm.
Họ và tên học sinh: …………………………………… Lớp: …………. Số báo danh: ………….
Chữ ký của CBCT: ……………………………………
HƯỚNG DẪN ĐÁP ÁN MÔN TOÁN LỚP 11 NĂM HỌC 2019-2020 : Mã đề 01 Câu 1 Đáp án Điểm a 𝜋𝜋 𝑠𝑠 = 0.5 1 điểm 1 6 + 𝑘𝑘2𝜋𝜋
2𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 − 1 = 0 ⇔ 𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 = 2 ⇔ � 5𝜋𝜋 (𝑘𝑘𝑘𝑘𝑘𝑘) 0.5
𝑠𝑠 = 6 + 𝑘𝑘2𝜋𝜋 b
Nhận xét : 𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 = 0 không thỏa mãn phương trình: vì 3𝑠𝑠𝑠𝑠𝑠𝑠2𝑠𝑠 = 0 . 0.25 1 điểm
𝑡𝑡𝑡𝑡𝑠𝑠𝑠𝑠 = 1 0.25
𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 ≠ 0 ptth: 3𝑡𝑡𝑡𝑡𝑠𝑠2𝑠𝑠 − 4𝑡𝑡𝑡𝑡𝑠𝑠𝑠𝑠 + 1 = 0 ⇔ �𝑡𝑡𝑡𝑡𝑠𝑠𝑠𝑠 = 13 0.25
𝑠𝑠 = 𝜋𝜋 + 𝑘𝑘𝜋𝜋 0.25 ⇔ � 4 (𝑘𝑘𝑘𝑘𝑘𝑘)
𝑠𝑠 = 𝑡𝑡𝑎𝑎𝑠𝑠𝑡𝑡𝑡𝑡𝑠𝑠 1 + 𝑘𝑘𝜋𝜋 3 1.c Đặ
t 𝑡𝑡 = 𝑠𝑠 + 𝜋𝜋 ptth:𝑠𝑠𝑠𝑠𝑠𝑠3𝑡𝑡 = √2𝑠𝑠𝑠𝑠𝑠𝑠(𝑡𝑡 − 𝜋𝜋) ⇔ 𝑠𝑠𝑠𝑠𝑠𝑠3𝑡𝑡 = 𝑠𝑠𝑠𝑠𝑠𝑠𝑡𝑡 − 𝑠𝑠𝑠𝑠𝑠𝑠𝑡𝑡 (*) 4 4
Nhận xét: 𝑠𝑠𝑠𝑠𝑠𝑠𝑡𝑡 = 0 không thỏa mãn pt vì 𝑠𝑠𝑠𝑠𝑠𝑠𝑡𝑡 = 0 0.5
điểm 𝑠𝑠𝑠𝑠𝑠𝑠𝑡𝑡 ≠ 0 pt(*) ⇔ 1 = 1 − 𝑐𝑐𝑐𝑐𝑠𝑠𝑡𝑡 ⇔ 𝑠𝑠𝑠𝑠𝑡𝑡3𝑡𝑡 − 𝑠𝑠𝑠𝑠𝑡𝑡2𝑡𝑡 + 𝑠𝑠𝑠𝑠𝑡𝑡𝑡𝑡 = 0 ⇔ 𝑠𝑠𝑠𝑠𝑡𝑡𝑡𝑡 = 0
𝑠𝑠𝑠𝑠𝑛𝑛2𝑡𝑡
𝑠𝑠𝑠𝑠𝑛𝑛3𝑡𝑡 0.25
⇔ 𝑡𝑡 = 𝜋𝜋 + 𝑘𝑘𝜋𝜋 ⇒ 𝑠𝑠 = 𝜋𝜋 + 𝑘𝑘𝜋𝜋. 0.25 2 4 Câu 2 a 8 0.5 Ta có 8 k 8−k 8
( 2x +1) = ∑C 2 −k x 1 điểm 8 k =0 0.25 0.25
Ycbt 8 − 𝑘𝑘 = 6 ⇒ 𝑘𝑘 = 2 vậy hệ số 𝑠𝑠6 trong khai triển 2 6 C 2 = 1792 8 b 1 n n k 1 Ta có n−k k (
+ x ) = ∑C ( ) x 2 n k = 2 0 1 0.25 n− 1 Ycbt 6 6 4 n−4 C ( ) = 4C ( ) 6 4
⇔ C = C ⇔ n − 6 = 4 ⇔ n = 10. n 2 n 2 n n 0.25 Câu 3 a 2 Ω = C = 66 0.25 12
1 điểm Gọi A biến cố chọn được hai viên bi cùng màu 2 2
Ω = C + C = 31 A 7 5 0.5 31 P( A ) = 0.25 66 b 2 Ω = C = 66 12
1 điểm Gọi B biến cố “ chọn 2 viên bi khác màu và tổng số ghi trên hai bi là số chẵn 0.25 ” 0.5 17 0.25 1 1 1 1
Ω = C C + C C = 17. P( B ) = B 4 2 3 3 vậy 66 Câu 4 a.  = +  = + 0.5 = x' x a x' 2 3  ⇒  ⇒ A'( 5; 3 − )
1 điểm T ( A ) A'( x'; y') u
thì y' = y + b y' = 1 − − 2 0.5 b. Đ 0.25
𝑐𝑐𝑜𝑜(𝐴𝐴) = (𝐴𝐴1) ⇒ Đ𝑐𝑐𝑜𝑜(𝐼𝐼) = 𝐼𝐼1(𝑠𝑠′; 𝑦𝑦′) ⇒ �𝑠𝑠′ = 1
𝑦𝑦′ = 2 ⇒ (𝐴𝐴1) �
𝑇𝑇â𝑚𝑚𝐼𝐼1(1; 2)
𝐴𝐴á𝑠𝑠 𝑘𝑘í𝑠𝑠ℎ 𝑅𝑅1 = 𝑅𝑅 = 3 0.25
𝑉𝑉(𝑠𝑠; −3)(𝐴𝐴1) = (𝐴𝐴′) ⇒ 𝑉𝑉(𝑠𝑠; −3)(𝐼𝐼1) = 𝐼𝐼1(𝑠𝑠′; 𝑦𝑦′) ⇒ �𝑠𝑠′ = −3 𝑦𝑦′ = −6 ⇒ (𝐴𝐴 0.25
1) �𝑇𝑇â𝑚𝑚: 𝐼𝐼′(−3; −6)
𝐴𝐴𝑘𝑘 ∶ 𝑅𝑅′ = 9 0.25
Phương trình (C’)(𝑠𝑠 + 3)2 + (𝑦𝑦 + 6)2 = 81 Câu 5
a. S ∈( SAC )  ⇒ S ∈( SBD 
S điểm chung thứ nhất. 0.25
1 điểm Gọi O là giao điểm AC và BD nên O là điểm chung của hai mặt phẳng.
( SAC ) ∩ ( SBD ) = SO 0.25 Vậy
( SAD ) ∩ ( SBC ) = ? S ∈( SAD ) 0.25  ⇒ S ∈( SBC ) S điểm chung 2 mp. Ta có AD / / BC   0.25
AD ⊂ ( SAD ) ⇒ ( SAD )∩( SBD ) = d 
BC ⊂ ( SBD )
Đường thẳng d đi qua S và d song song với AD. 0.5
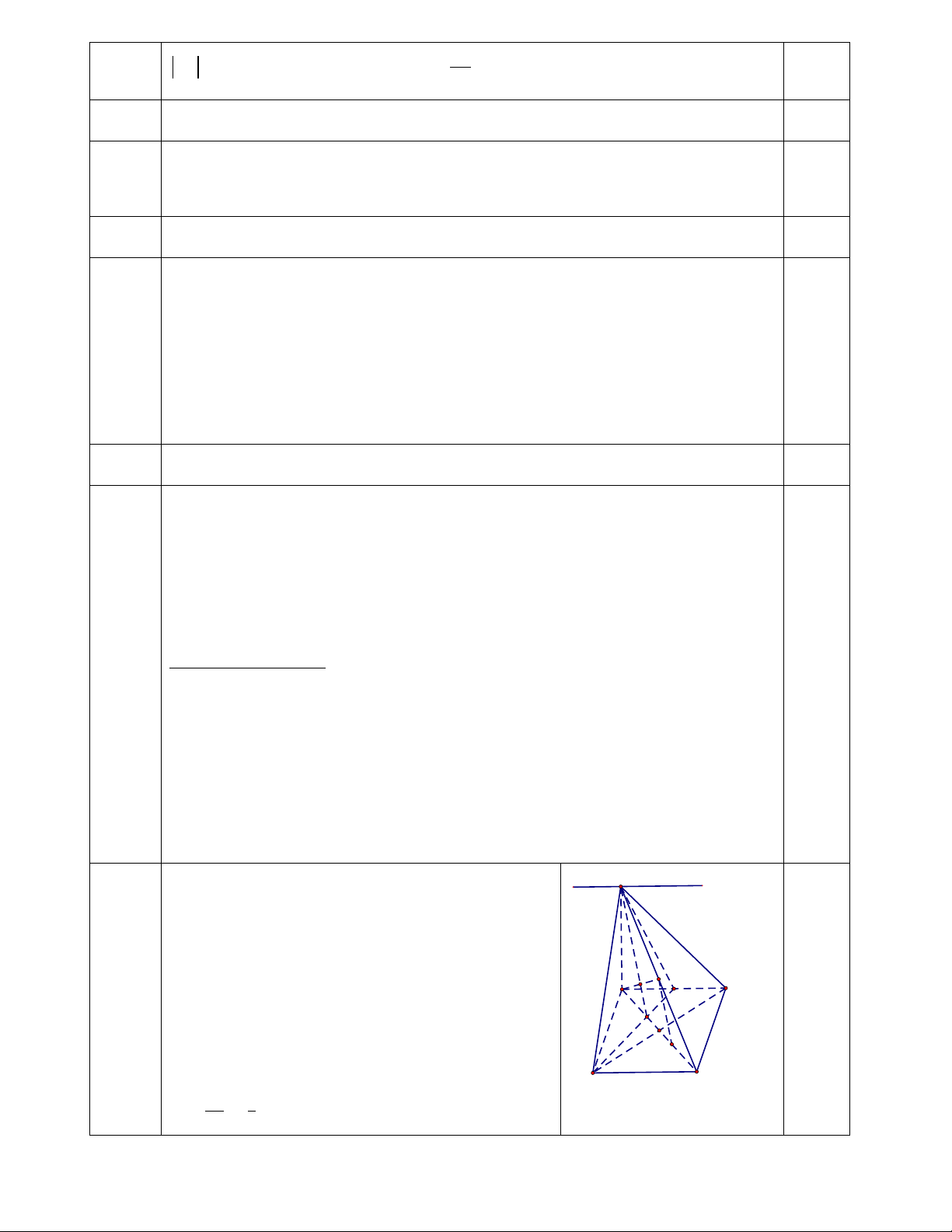
Gọi G giao điểm AC và AM, suy ra G là trọng tâm S điểm tam giác ABD.
Gọi I là giao điểm AN và SG.
Ta có 𝐼𝐼 ∈ 𝐴𝐴𝐴𝐴 𝑣𝑣à 𝐼𝐼 ∈ 𝑆𝑆𝑆𝑆 N ⊂ 0.25
( SAM ) ⇒ I = AN ∩ ( SAM ) A I D M
Gọi E là trung điểm GC . Ta có NE là đường trung G bình tam giác SGC. O E
Tương tự IG là đường trung bình tam giác ANE B C Vậy 𝐴𝐴𝐴𝐴 = 1 0.25 𝐴𝐴𝐴𝐴 2
HƯỚNG DẪN ĐÁP ÁN MÔN TOÁN LỚP 11 NĂM HỌC 2019-2020 : Mã đề 02 Câu 1 Đáp án Điểm a 𝜋𝜋 𝑠𝑠 = 0.5 1 điểm √3 6 + 𝑘𝑘2𝜋𝜋
2𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 − √3 = 0 ⇔ 𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 = 2 ⇔ � −𝜋𝜋 (𝑘𝑘𝑘𝑘𝑘𝑘) 0.5
𝑠𝑠 = 6 + 𝑘𝑘2𝜋𝜋 b
Nhận xét : 𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 = 0 không thỏa mãn phương trình: vì 𝑠𝑠𝑠𝑠𝑠𝑠2𝑠𝑠 = 0 . 0.25 1 điểm 0.25
𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 ≠ 0 ptth: 𝑡𝑡𝑡𝑡𝑠𝑠2𝑠𝑠 − 3𝑡𝑡𝑡𝑡𝑠𝑠𝑠𝑠 + 2 = 0 ⇔ �𝑡𝑡𝑡𝑡𝑠𝑠𝑠𝑠 = 1
𝑡𝑡𝑡𝑡𝑠𝑠𝑠𝑠 = 2 0.25 ⇔ �
𝑠𝑠 = 𝜋𝜋 + 𝑘𝑘𝜋𝜋 4 (𝑘𝑘𝑘𝑘𝑘𝑘) 0.25
𝑠𝑠 = 𝑡𝑡𝑎𝑎𝑠𝑠𝑡𝑡𝑡𝑡𝑠𝑠2 + 𝑘𝑘𝜋𝜋 1.c
Đặt 𝑡𝑡 = 𝑠𝑠 − 𝜋𝜋
ptth:𝑠𝑠𝑠𝑠𝑠𝑠3𝑡𝑡 = √2𝑠𝑠𝑠𝑠𝑠𝑠(𝑡𝑡 + 𝜋𝜋) ⇔ 𝑠𝑠𝑠𝑠𝑠𝑠3𝑡𝑡 = 𝑠𝑠𝑠𝑠𝑠𝑠𝑡𝑡 + 𝑠𝑠𝑠𝑠𝑠𝑠𝑡𝑡 (*) 4 4
Nhận xét: 𝑠𝑠𝑠𝑠𝑠𝑠𝑡𝑡 = 0 không thỏa mãn pt vì 𝑠𝑠𝑠𝑠𝑠𝑠𝑡𝑡 = 0 0.5
điểm 𝑠𝑠𝑠𝑠𝑠𝑠𝑡𝑡 ≠ 0 pt(*) ⇔ 1 = 1 + 𝑐𝑐𝑐𝑐𝑠𝑠𝑡𝑡 ⇔ 𝑠𝑠𝑠𝑠𝑡𝑡3𝑡𝑡 + 𝑠𝑠𝑠𝑠𝑡𝑡2𝑡𝑡 + 𝑠𝑠𝑠𝑠𝑡𝑡𝑡𝑡 = 0 ⇔ 𝑠𝑠𝑠𝑠𝑡𝑡𝑡𝑡 = 0
𝑠𝑠𝑠𝑠𝑛𝑛2𝑡𝑡
𝑠𝑠𝑠𝑠𝑛𝑛3𝑡𝑡 0.25
⇔ 𝑡𝑡 = 𝜋𝜋 + 𝑘𝑘𝜋𝜋 ⇒ 𝑠𝑠 = 3𝜋𝜋 + 𝑘𝑘𝜋𝜋. 0.25 2 4 Câu 2 a 11 0.5 Ta có 11 k 11−k 11
( 3x +1) = ∑C 3 −k x 1 điểm 11 k =0 0.25
Ycbt 11 − 𝑘𝑘 = 7 ⇒ 𝑘𝑘 = 4 vậy hệ số 𝑠𝑠6 trong khai triển 4 7
C 3 = 721710. 11 0.25 b 1 n n k 1 Ta có n−k k (
+ x ) = ∑C ( ) x 3 n k = 3 0 1 0.25 n− 1 Ycbt 7 7 5 n−5 C ( ) = 9C ( ) 7 5
⇔ C = C ⇔ n − 7 = 5 ⇔ n = 12. n 3 n 3 n n 0.25 Câu 3 a 2 Ω = C = 91 0.25 14
1 điểm Gọi A biến cố chọn được hai viên bi cùng màu 2 2
Ω = C + C = 46 A 9 5 0.5 46 P( A ) = 0.25 91 b 2 Ω = C = 91 14 1 điểm 0.25
Gọi B biến cố “ chọn 2 viên bi khác màu và tổng số ghi trên hai bi là số lẻ” 0.5 1 1 1 1
Ω = C C + C C = 23. 0.25 B 5 3 4 2 23 P( B ) = 91 Câu 4 a.  = +  = 0.5 = x' x a x' 2  ⇒ 
⇒ A'( 2;2 )
1 điểm T ( A ) A'( x'; y') u
thì y' = y + b y' = 2 0.5 b. Đ 0.25
𝑐𝑐𝑜𝑜(𝐴𝐴) = (𝐴𝐴1) ⇒ Đ𝑐𝑐𝑜𝑜(𝐼𝐼) = 𝐼𝐼1(𝑠𝑠′; 𝑦𝑦′) ⇒ �𝑠𝑠′ = −3
𝑦𝑦′ = −1 ⇒ (𝐴𝐴1) � 𝑇𝑇â𝑚𝑚𝐼𝐼1(−3; −1)
𝐴𝐴á𝑠𝑠 𝑘𝑘í𝑠𝑠ℎ 𝑅𝑅1 = 𝑅𝑅 = 4 0.25
𝑉𝑉(𝑂𝑂; −2)(𝐴𝐴1) = (𝐴𝐴′) ⇒ 𝑉𝑉(𝑂𝑂; −2)(𝐼𝐼1) = 𝐼𝐼1(𝑠𝑠′; 𝑦𝑦′) ⇒ �𝑠𝑠′ = 6 𝑦𝑦′ = 2 ⇒ (𝐴𝐴 0.25
1) �𝑇𝑇â𝑚𝑚: 𝐼𝐼′(6; 2)
𝐴𝐴𝑘𝑘 ∶ 𝑅𝑅′ = 8 0.25
Phương trình (C’)(𝑠𝑠 − 6)2 + (𝑦𝑦 − 2)2 = 64 Câu 5 a. S ∈( SAC )  ⇒
1 điểm S ∈( SBD  S điểm chung thứ nhất. 0.25
Gọi O là giao điểm AC và BD nên O là điểm chung của hai mặt phẳng.
( SAC ) ∩ ( SBD ) = SO 0.25 Vậy
( SAB ) ∩ ( SCD ) = ? AB / / CD  0.25 S ∈( SAB )    ⇒
AB ⊂ ( SAB )  ⇒ ( SAB )∩( SCD ) = d S ∈( SCD ) S điểm chung 2 mp. Ta có 
CD ⊂ ( SCD ) 0.25
Đường thẳng d đi qua S và d song song với AB. b.
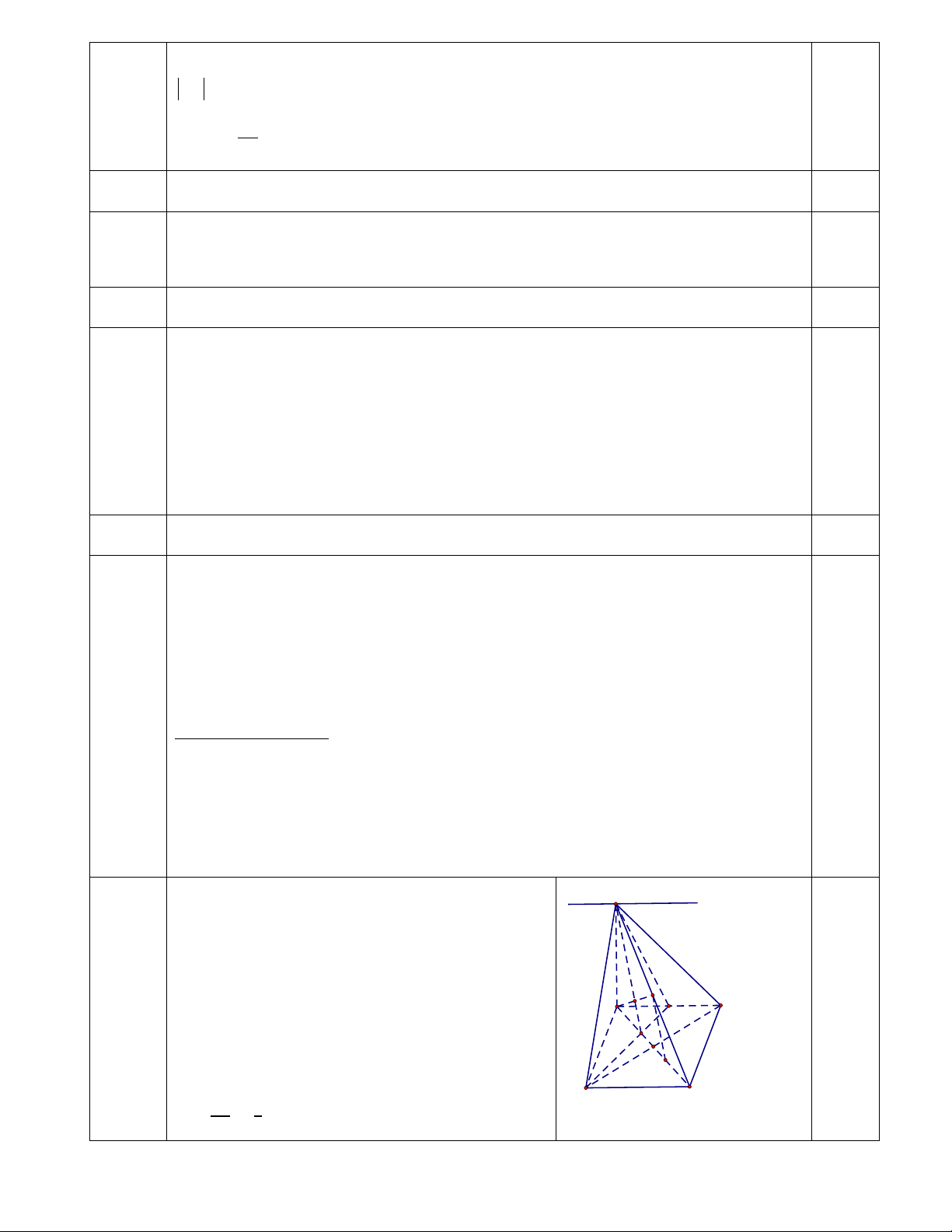
Gọi G giao điểm AC và DN, suy ra G là trọng S tâm tam giác ABD. 0.5
điểm Gọi I là giao điểm AM và SG.
Ta có 𝐼𝐼 ∈ 𝐴𝐴𝑆𝑆 𝑣𝑣à 𝐼𝐼 ∈ 𝑆𝑆𝑆𝑆 ⊂ M 0.25
( SDN ) ⇒ I = AM ∩ ( SDN ) A I B N
Gọi E là trung điểm GC . Ta có ME là đường G trung bình tam giác SGC. O E
Tương tự IG là đường trung bình tam giác AME. D C Vậy 𝐴𝐴𝐴𝐴 = 1 0.25 𝐴𝐴𝐴𝐴 2
Document Outline

• de_11-2019-2020_2ab06526f0