Đề kiểm tra theo bài học ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
Tài liệu gồm 90 trang, tuyển tập các đề kiểm tra theo bài học chủ đề ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số môn Toán 12. Các đề kiểm tra được biên soạn theo định dạng trắc nghiệm mới nhất, với cấu trúc gồm 03 phần: Câu trắc nghiệm nhiều phương án lựa chọn; Câu trắc nghiệm đúng hoặc sai; Câu trắc nghiệm trả lời ngắn. Thời gian làm bài kiểm tra là 90 phút. Đề kiểm tra có đáp án và hướng dẫn giải chi tiết. Mời bạn đọc đón xem!
Chủ đề: Chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số 375 tài liệu
Môn: Toán 12 3.9 K tài liệu
Tác giả:
Preview text:
BÀI 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ VÀ CỰC TRỊ
Môn Toán – Khối 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề). ĐỀ SỐ 1
Họ, tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lớp: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1.
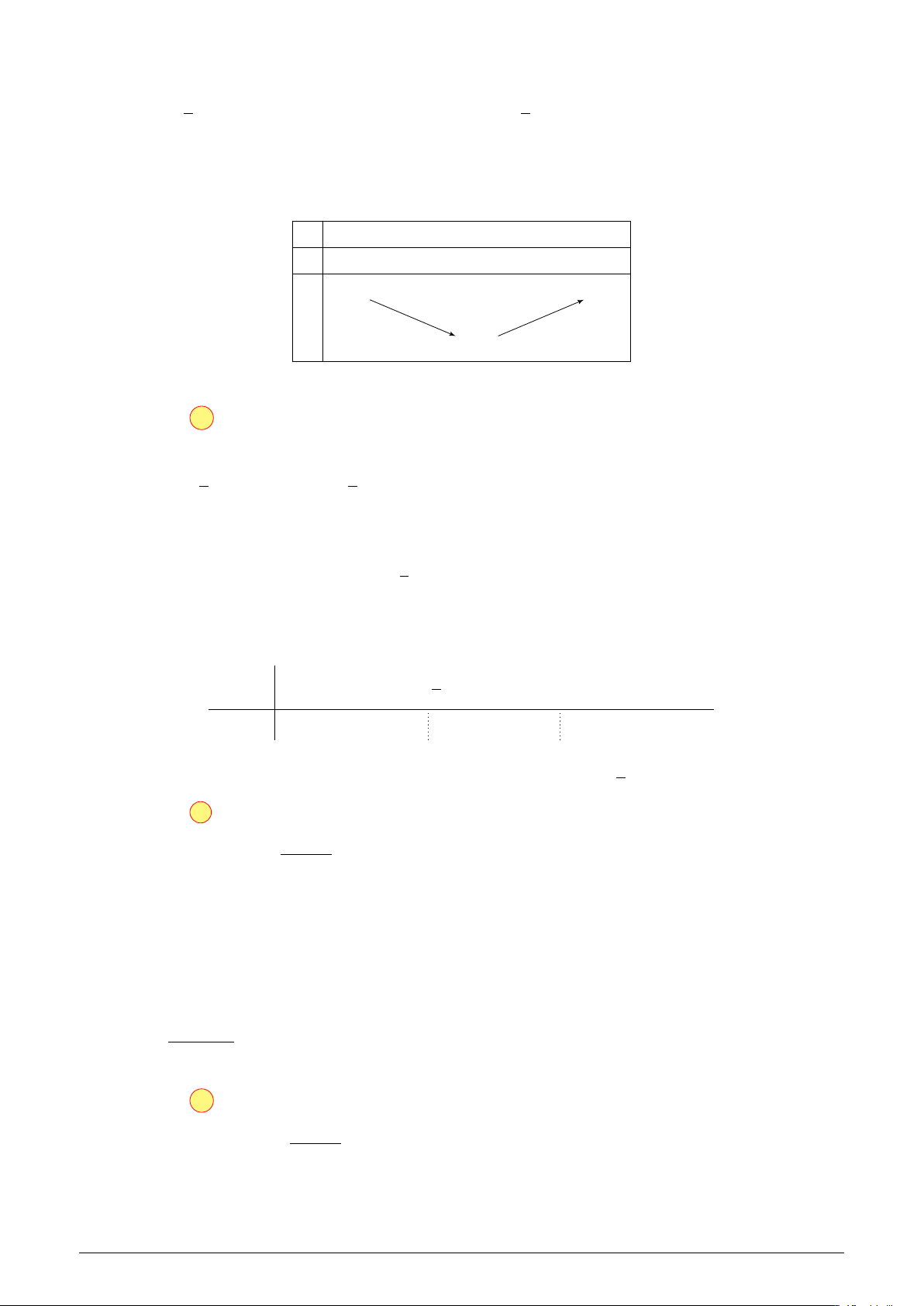
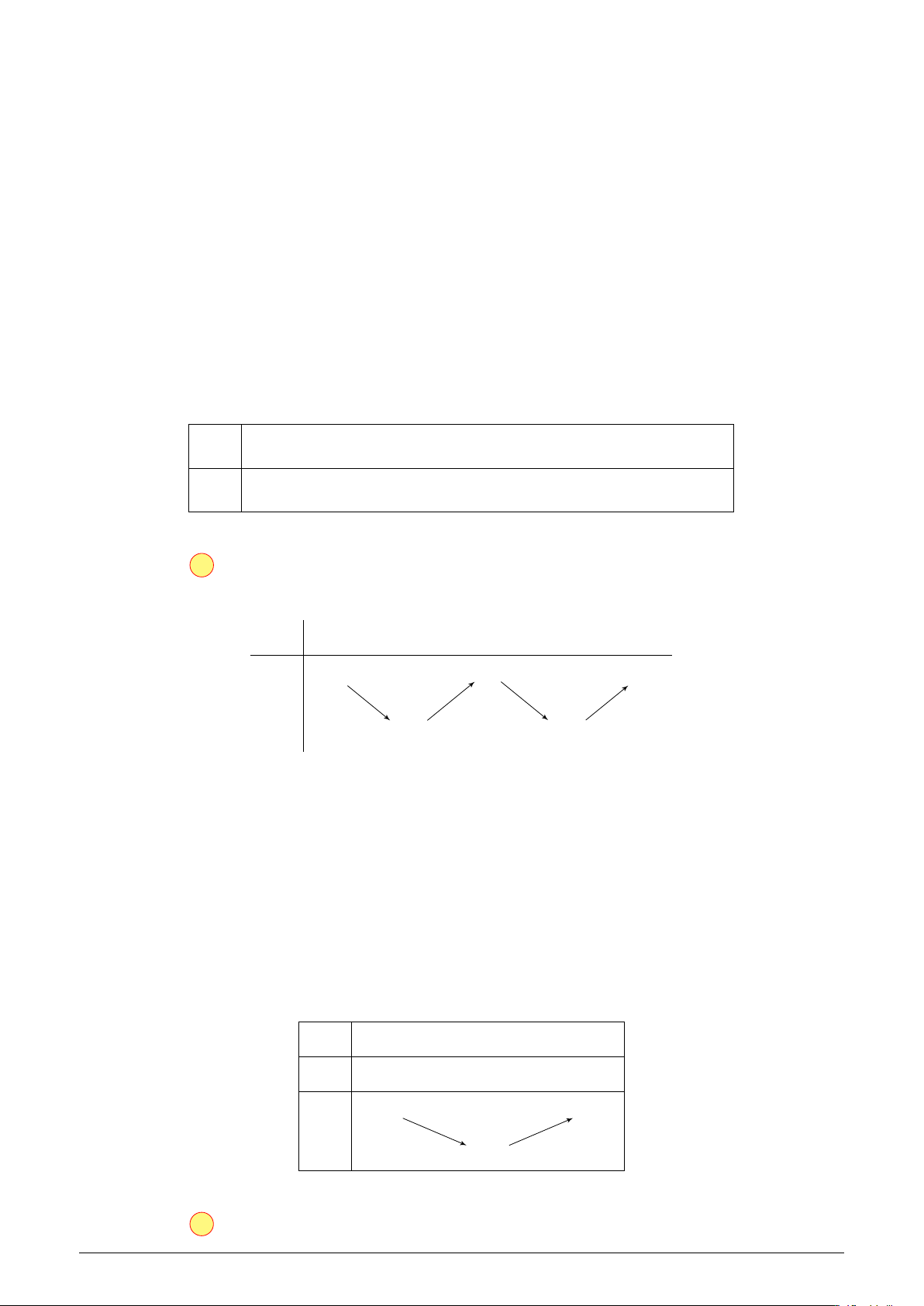
Cho hàm số f (x) có bảng biến thiên như MDD-122
hình bên. Hàm số đã cho đồng biến trên x −∞ −1 0 1 +∞ khoảng nào dưới đây? y0 + 0 − 0 + 0 − A. (0; 1). B. (2; +∞). 4 4 C. (1; +∞). D. (−1; 1). y −∞ 1 −∞
Câu 2. Cho hàm số y = f (x) xác định trên R\{2}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: x −∞ 2 +∞ f 0(x) − − 1 +∞ f (x) −∞ 1
Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số nghịch biến với mọi x 6= 2.
B. Hàm số nghịch biến trên tập R\{2}.
C. Hàm số nghịch biến trên mỗi khảng (−∞; 2) và (2; +∞).
D. Hàm số đồng biến trên mỗi khảng (−∞; 2) và (2; +∞). Câu 3.
Cho hàm số y = f (x) xác định trên R và có bảng x −∞ 10 12 +∞
biến thiên như hình vẽ bên. Hàm số y = f (x) y0 + 0 − 0 + đạt cực đại tại −∞ A. x = 10. B. x = 8. −3 y C. x = 12. D. x = 17. −∞ 3
Câu 4. Hàm số y = x3 − 3x2 + 2 nghịch biến trên khoảng nào trong các khoảng sau đây? A. (2; +∞). B. (−∞; 0). C. (−∞; +∞). D. (0; 2).
Câu 5. Trong các hàm số sau, hàm số nào đồng biến trên (−∞; +∞)? x + 1 x − 1 A. y = . B. y = −x3 − 3x. C. y = x3 + x. D. y = . x + 3 x − 2
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 1
Câu 6. Hỏi hàm số y = x4 − 2x2 + 3 đồng biến trên khoảng nào? A. R.
B. (−∞; −1) và (0; 1).
C. (−1; 0) và (1; +∞).
D. (−1; 0) và (0; 1).
Câu 7. Hàm số y = x4 − 2 nghịch biến trên khoảng nào dưới đây? 1 1 A. −∞; . B. (0; +∞). C. ; +∞ . D. (−∞; 0). 2 2
Câu 8. Hàm số y = −x4 + 2x3 − 2x − 1 nghịch biến trên khoảng nào sau đây? 1 1 A. −∞; − . B. − ; +∞ . C. (−∞; +∞). D. (−∞; 1). 2 2 2x + 5
Câu 9. Cho hàm số y =
. Tìm mệnh đề đúng trong các mệnh đề sau x − 2
A. Hàm số nghịch biến trên khoảng (−∞; 3).
B. Hàm số nghịch biến trên (−∞; −2) ∪ (−2; +∞).
C. Hàm số nghịch biến trên R \ {2}.
D. Hàm số nghịch biến trên các khoảng (−∞; 2) và (2; +∞). 2x + 1
Câu 10. Cho hàm số y = . Mệnh đề đúng là x + 1
A. Hàm số đồng biến trên các khoảng (−∞; −1) và (−1; +∞), nghịch biến trên (−1; 1).
B. Hàm số đồng biến trên tập R.
C. Hàm số đồng biến trên các khoảng (−∞; −1) và (−1; +∞).
D. Hàm số nghịch biến trên các khoảng (−∞; −1) và (−1; +∞).
Câu 11. Trong 8 phút kể từ khi xuất phát, độ cao h (tính bằng mét) của khinh khí cầu vào tời
điểm t phút được cho bởi công thức h(t) = 6t3 − 81t2 + 324t. Hỏi độ cao của khinh khí cầu
giảm trong khoảng thời gian nào?
A. Từ phút thứ 2 đến phút thứ 6.
B. Từ phút thứ 3 đến phút thứ 6.
C. Từ phút thứ 4 đến phút thứ 8.
D. Từ phút thứ 6 đến phút thứ 8. Câu 12. ax + b
Đường cong ở hình bên là đồ thị hàm số y = , với a, b, c, d y cx + d
là các số thực. Mệnh đề nào dưới đây là đúng?
A. y0 < 0, ∀x 6= 1.
B. y0 < 0, ∀x 6= 2.
C. y0 > 0, ∀x 6= 2.
D. y0 > 0, ∀x 6= 1. 2 O x 1
Câu 13. Tìm giá trị cực tiểu yCT của hàm số y = −x3 + 3x − 4. A. yCT = −1. B. yCT = −2. C. yCT = 1. D. yCT = −6.
Câu 14. Cho hàm số y = 7x3 + 9x2 − 3x − 4. Khẳng định nào sau đây là sai? 1
A. Giá trị cực đại y = 1.
B. Hàm số đạt cực tiểu tại x = . 7 1
C. Giá trị cực tiểu y = .
D. Hàm số đạt cực đại tại x = −1. 7
Câu 15. Gọi A, B là hai điểm cực trị của đồ thị hàm số y = x3 − 3x2 + 4. Tính diện tích S của
tam giác OAB với O là gốc tọa độ.√ A. S = 8. B. S = 3. C. S = 2. D. S = 4.
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 2
Câu 16. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số y = x3 − 3x2 + 4 bằng √ √ A. 2 2. B. 2 5. C. 4. D. 2.
Câu 17. Đồ thị của hàm số y = x3 − 3x2 − 9x + 1 có hai điểm cực trị A và B. Điểm nào dưới
đây thuộc đường thẳng AB? A. N(1; −10). B. Q(−1; 10). C. M(0; −1). D. P(1; 0).
Câu 18. Cho hàm số y = f (x) có tập xác định [−8; 8]\{2} và có bảng biến thiên như hình bên
dưới. Khẳng định nào sau đây là khẳng định đúng? x −8 −1 2 4 8 y0 + 0 + + 0 − +∞ 3 y 1 −2 −∞ −∞
A. Điểm cực tiểu của đồ thị là (−8; −2).
B. Hàm số đồng biến trên khoảng (−8; 2).
C. Hàm số đạt cực trị tại x = −1.
D. Hàm số đồng biến trên khoảng (−1; 4). Câu 19.
Cho hàm số có đồ thị như hình bên. Khẳng định nào sai? 3 y 3 3 −
A. Hàm số có một cực tiểu tại x =
và đạt cực đại tại x = 0. 4 4 4 x O 113 −1
B. Giá trị cực đại y = −1 và giá trị cực tiểu y = − . 32 3
C. Hàm số có một cực tiểu tại x = − . 4 3
D. Hàm số có một cực đại tại x = − . 4 113 − 32
Câu 20. Cho hàm số y = f (x) liên tục trên R và có f 0(x) = x3(x − 2019)2(x − 2020). Tìm số
cực trị của hàm số y = f (x). A. 4. B. 3. C. 1. D. 2. Câu 21.
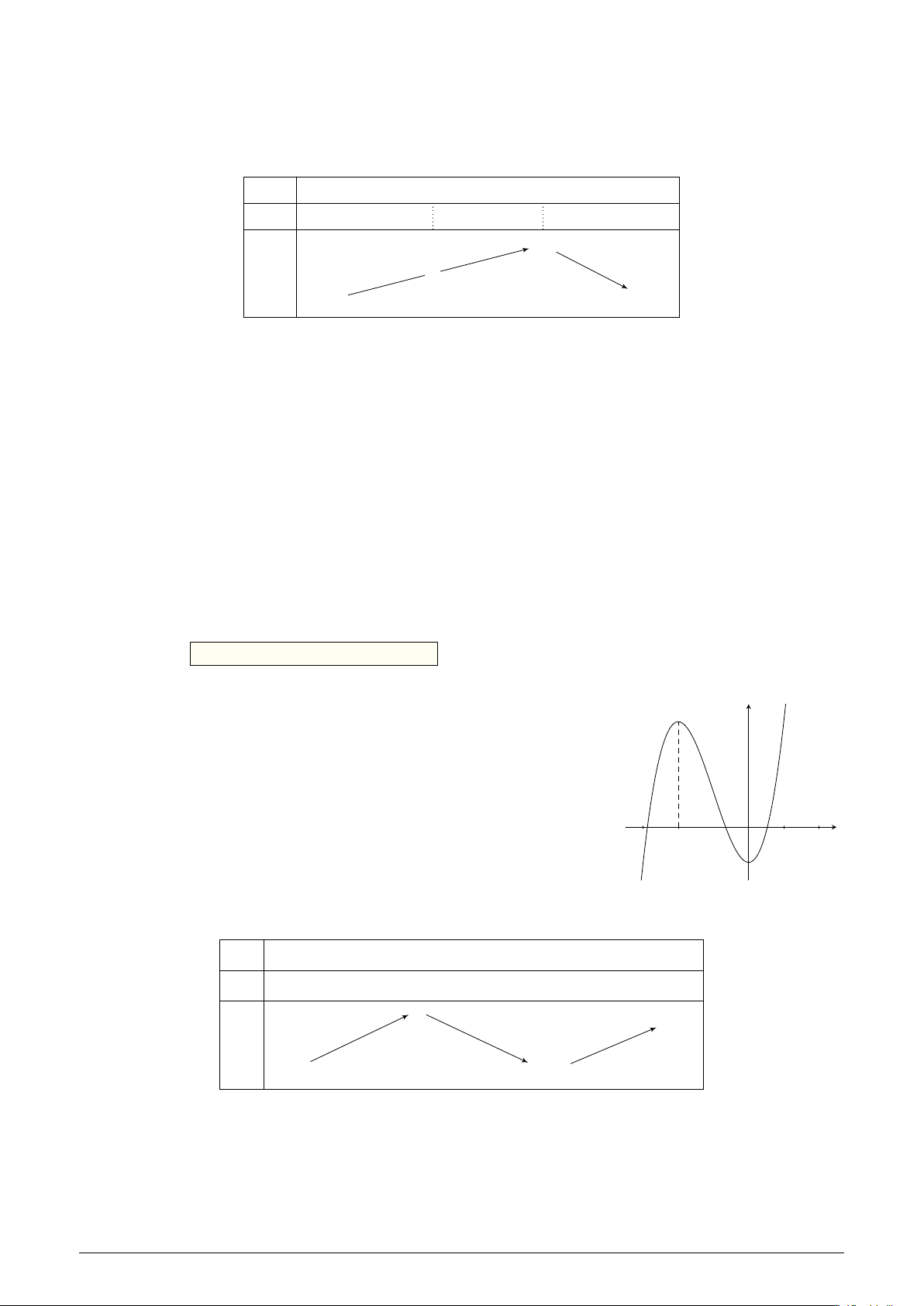
Cho hàm số f (x) có đạo hàm trên R là hàm số f 0(x). Biết đồ thị của y
hàm số f 0(x) được cho như hình vẽ. Hàm số y = f (x) nghịch biến trên khoảng nào sau đây? A. (−∞; −3). B. (0; 1). C. (−3; −2). D. (−∞; −1). O − x 3 −2 1 Câu 22.
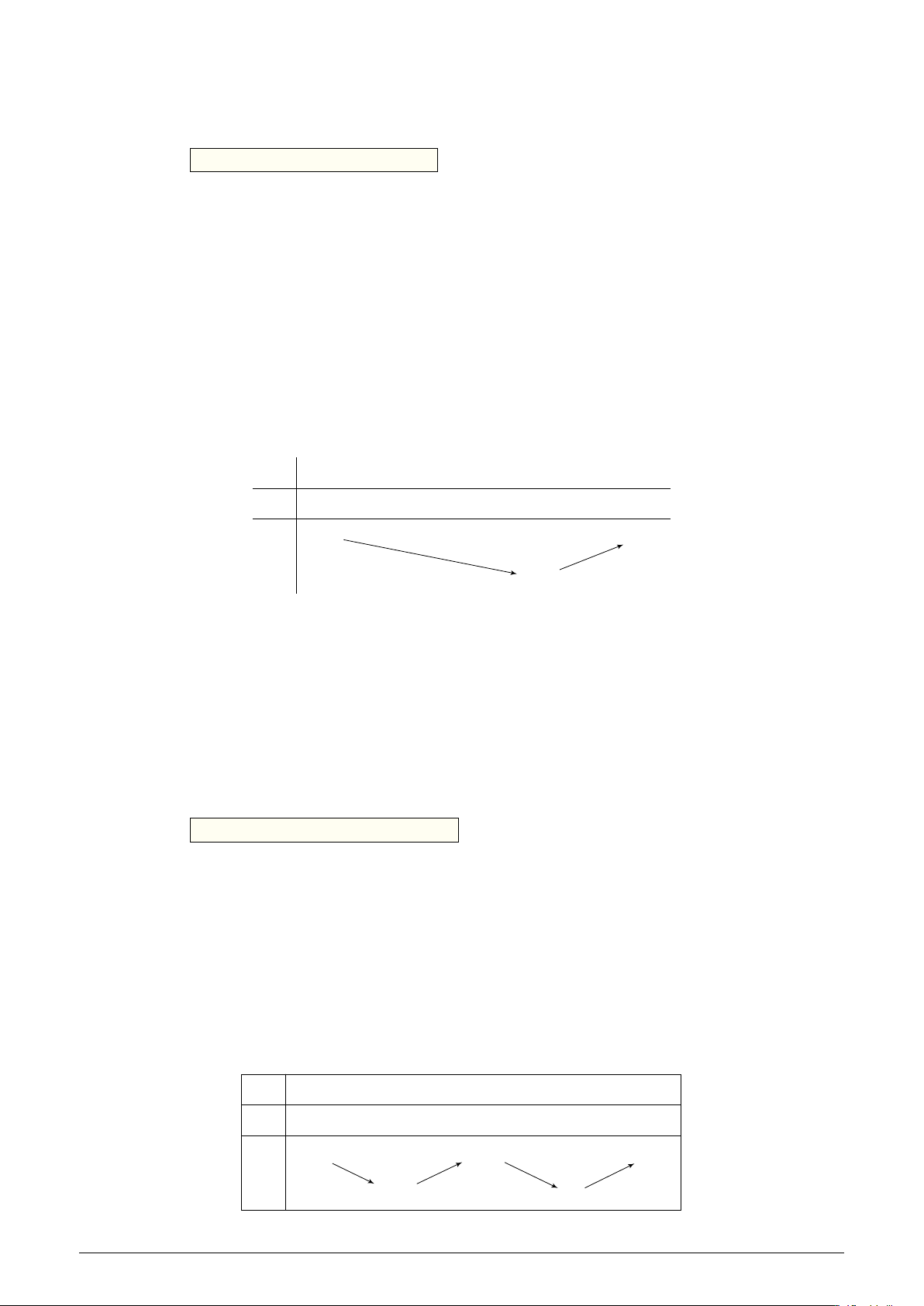
Cho hàm đa thức bậc năm y = f (x). Đồ thị hàm số y = f 0(x) như y
hình vẽ. Hàm số y = f (x) có bao nhiêu điểm cực tiểu? A. 4. B. 2. O 1 3 C. 3. D. 1. x
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 3 1 Câu 23. Hàm số y =
x3 + (m + 1)x2 − (m + 1)x + 1 đồng biến trên tập xác định của nó khi 3 và chỉ khi A. −2 < m < 1. B. −2 ≤ m ≤ −1.
C. −2 < m < −1. D. −1 ≤ m ≤ 2. 1
Câu 24. Tìm tất cả các giá trị thực của tham số m để hàm số y = − x3 − mx2 + (2m − 3)x − 3
m + 2 nghịch biến trên R. A. m ≤ −3, m ≥ 1. B. −3 < m < 1. C. −3 ≤ m ≤ 1. D. m ≤ 1.
Câu 25. Cho hàm số f (x) = x3 − 3(m + 1)x2 + 3m(m + 2)x. Có bao nhiêu giá trị nguyên của
tham số thực m để hàm số nghịch biến trên khoảng (0; 1)? A. 0. B. 1. C. 2. D. Vô số. x + m2
Câu 26. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = đồng biến trên x + 4
từng khoảng xác định của nó? A. 5. B. 1. C. 3. D. 2. x + 2 − m
Câu 27. Tìm tất cả các giá trị thực của tham số m để hàm số y = nghịch biến trên x + 1
các khoảng mà nó xác định? A. m < −3. B. m ≤ 1. C. m < 1. D. m ≤ −3. x − 1
Câu 28. (TN.2017-2018). Tìm tất cả các giá trị thực của tham số m để hàm số y = nghịch x − m
biến trên khoảng (−∞; 2). A. m > 1. B. m ≥ 1. C. m > 2. D. m ≥ 2.
Câu 29. Tìm tất cả các giá trị thực của m để hàm số y = x3 − 3x2 + (m + 1)x + 2 có hai điểm cực trị. A. m < 2. B. m ≤ 2. C. m > 2. D. m < −4.
Câu 30. Cho hàm số y = 2x3 + 3(m − 1)x2 + 6(m − 2)x − 18. Tập hợp tất cả các giá trị của
tham số m để hàm số có hai điểm cực trị thuộc khoảng (−5; 5) là
A. (−∞; −3) ∪ (7; +∞). B. (−3; +∞) \ {3}. C. (−∞; 7) \ {3}. D. (−3; 7) \ {3}.
Câu 31. Cho hàm số y = (m + 1)x4 − mx2 + 3. Tìm tất cả các giá trị thực của tham số m để
hàm số có ba điểm cực trị.
A. m ∈ (−∞; −1) ∪ [0; +∞). B. m ∈ (−1; 0).
C. m ∈ (−∞; −1] ∪ [0; +∞).
D. m ∈ (−∞; −1) ∪ (0; +∞).
Câu 32. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x4 + 2 m2 − m − 6 x2 +
m − 1 có 3 điểm cực trị? A. 5. B. 4. C. 3. D. 6.
Câu 33. Cho hàm số f (x) có đạo hàm trên R và có dấu của f 0(x) như sau x −∞ −1 1 2 3 +∞ f 0(x) + 0 − 0 − 0 + 0 −
Hàm số y = f (2 − 3x) nghịch biến trên khoảng 1 1 1 1 1 A. − ; 0 . B. 0; . C. − ; . D. − ; 0 . 4 4 3 3 2
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 4
Câu 34. Cho hàm số y = f (x) liên tục và có đạo hàm trên R. Hàm số y = f 0(x) có đồ thị như hình bên dưới. y y = f 0(x) 2 x O 1 2
Hàm số g(x) = f 1 + 2x − x2 đồng biến trên khoảng nào dưới đây? A. (1; 2). B. (0; 1). C. (−∞; 1). D. (1; +∞).
Câu 35. (TN.2019). Cho hàm số f (x), bảng biến thiên của hàm số f 0(x) như hình vẽ bên dưới x −∞ −1 0 1 +∞ +∞ 2 +∞ f 0(x) −3 −1
Số điểm cực trị của hàm số y = f (x2 + 2x) là A. 3. B. 9. C. 5. D. 7.
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số y = f (x) có bảng biến thiên như sau x −∞ 0 1 +∞ y0 + 0 + 0 − 2 y 0 −∞ −∞
Xét tính đúng sai của các khẳng định sau:
a) Hàm số đồng biến trên (−∞; 2).
b) Hàm số nghịch biến trên (1; +∞).
c) Hàm số có hai điểm cực trị.
d) Hàm số đạt cực đại tại x = 1. Câu 2.
Cho hàm số y = f (x) có đồ thì như hình vẽ bên. Xét tính đúng y
sai của các khẳng định sau:
a) Hàm số đã cho nghịch biến trên khoảng (−2, 0).
b) Hàm số đã cho đồng biến trên khoảng (−1; +∞).
c) Hàm số đã cho đồng biến trên khoảng (2; +∞). O x
d) Hàm số đạt cực tiểu tại x = −1. −3 −2 1 2 −1
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 5
Câu 3. Cho hàm số y = f (x) xác định trên R và có đạo hàm f 0(x) = 3x3 − 3x2, ∀x ∈ R. Xét
tính đúng sai của các khẳng định sau:
a) Hàm số đồng biến trên khoảng (1; +∞).
b) Hàm số nghịch biến trên khoảng (−1; 1).
c) Đồ thị hàm số có hai điểm cực trị.
d) Đồ thị hàm số có một điểm cực tiểu.
Câu 4. Cho hàm số y = f (x) = x4 − 2x2 − 3. Xét tính đúng sai của các khẳng định sau:
a) Hàm số đã cho đạt cực đại tại x = 0.
b) Hàm số đã cho đạt cực tiểu tại x = −3.
c) Hàm số đã cho có giá trị cực đại và cực tiểu lần lượt là −4, −3.
d) Đồ thị hàm số g(x) = f (x) + 3 có điểm cực đại là (0; 0) .
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Câu 1. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số y = −x3 + 3x + 2 bằng bao nhiêu?
(kết quả làm tròn đến hàng phần trăm) KQ:
Câu 2. Cho hàm số y = x4 − 8x2 + 10 có đồ thị (C). Gọi A, B, C là ba điểm cực trị của đồ thị
(C). Tính diện tích S của tam giác ABC. KQ:
Câu 3. Đồ thị hàm số y = x3 − 3x2 + 2ax + b có điểm cực tiểu A(2; −2). Khi đó a + b bằng bao nhiêu? KQ:
Câu 4. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = −x3 − (m − 1)x2 + 3mx + 1
nghịch biến trên R? KQ: −x + 6
Câu 5. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = đồng biến trên x + m (10; +∞)? KQ:
Câu 6. Tìm giá trị thực của tham số m để đồ thị hàm số y = −x3 + 3mx + 1 có hai điểm cực
trị A, B sao cho tam giác OAB vuông tại O, với O là gốc tọa độ. KQ: —HẾT—
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 6
BÀI 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ VÀ CỰC TRỊ
Môn Toán – Khối 12
Thời gian làm bài: 90 phút (không kể thời gian phát đề). ĐỀ SỐ 1
Họ, tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lớp: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một phương án. Câu 1.
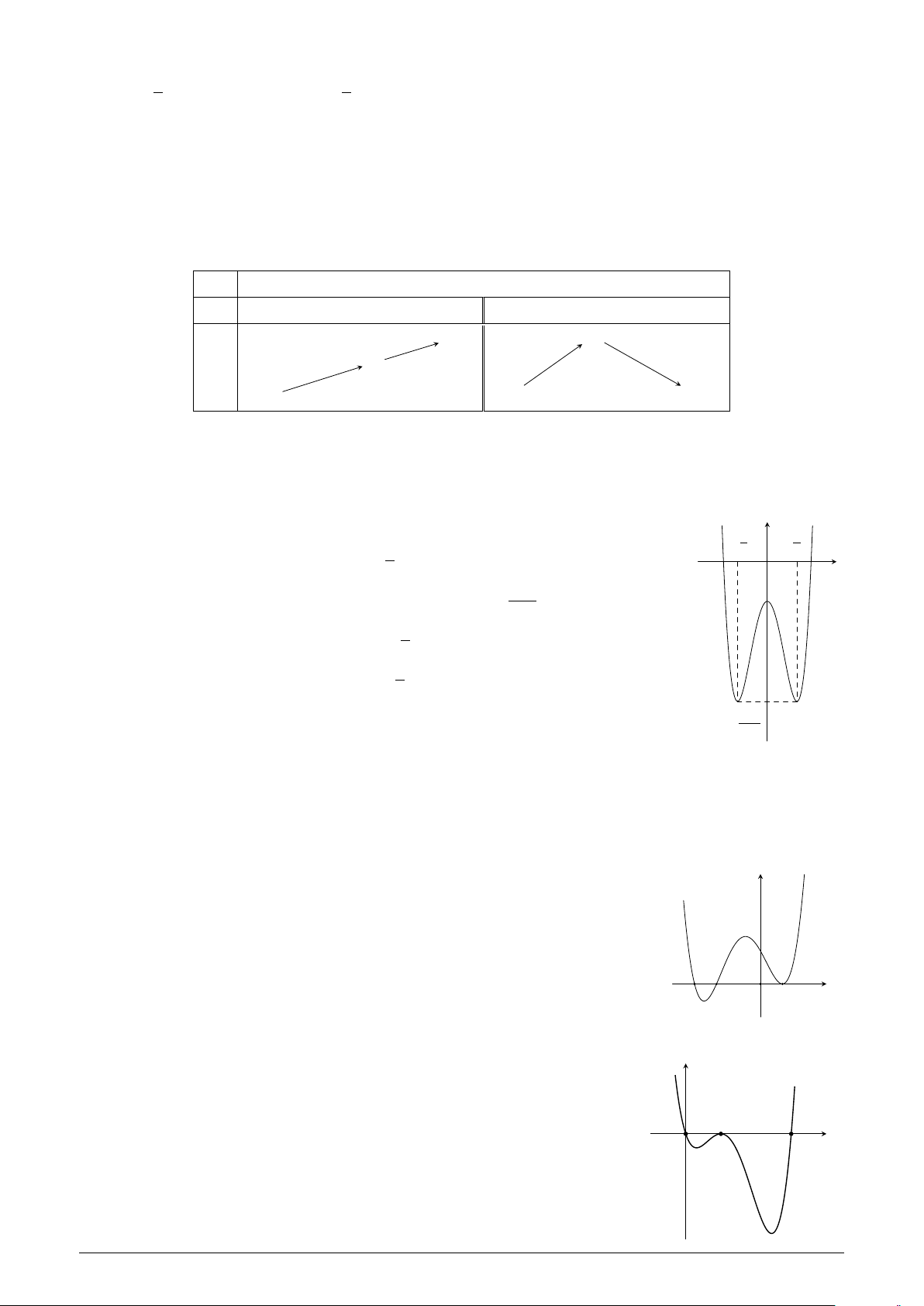
Cho hàm số f (x) có bảng biến thiên như MDD-122
hình bên. Hàm số đã cho đồng biến trên x −∞ −1 0 1 +∞ khoảng nào dưới đây? y0 + 0 − 0 + 0 − A. (0; 1). B. (2; +∞). 4 4 C. (1; +∞). D. (−1; 1). y −∞ 1 −∞ Lời giải.
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trong (0; 1).
Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 2. Cho hàm số y = f (x) xác định trên R\{2}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: x −∞ 2 +∞ f 0(x) − − 1 +∞ f (x) −∞ 1
Trong các khẳng định sau, khẳng định nào đúng?
A. Hàm số nghịch biến với mọi x 6= 2.
B. Hàm số nghịch biến trên tập R\{2}.
C. Hàm số nghịch biến trên mỗi khảng (−∞; 2) và (2; +∞).
D. Hàm số đồng biến trên mỗi khảng (−∞; 2) và (2; +∞). Lời giải.
Từ bảng biến thiên, ta thấy y0 < 0 ∀x 6= 2.
Suy ra, hàm số nghịch biến trên mỗi khoảng xác định.
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 3.
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 1
Cho hàm số y = f (x) xác định trên R và có bảng x −∞ 10 12 +∞
biến thiên như hình vẽ bên. Hàm số y = f (x) y0 + 0 − 0 + đạt cực đại tại −∞ A. x = 10. B. x = 8. −3 y C. x = 12. D. x = 17. −∞ 3 Lời giải.
Dựa vào bảng biến thiên ta thấy hàm số đạt cực đại tại x = 10.
Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 4. Hàm số y = x3 − 3x2 + 2 nghịch biến trên khoảng nào trong các khoảng sau đây? A. (2; +∞). B. (−∞; 0). C. (−∞; +∞). D. (0; 2). Lời giải.
Hàm số có tập xác định D = R. "x = 0
y0 = 3x2 − 6x, y0 = 0 ⇔ x = 2.
Với x = 0, y = 2; với x = 2, y = −2. Ta có bảng biến thiên sau x −∞ 0 2 +∞ y0 + 0 − 0 + 2 +∞ y −∞ −2
Từ đó ta được hàm số nghịch biến trên (0; 2).
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 5. Trong các hàm số sau, hàm số nào đồng biến trên (−∞; +∞)? x + 1 x − 1 A. y = . B. y = −x3 − 3x. C. y = x3 + x. D. y = . x + 3 x − 2 Lời giải. x + 1 x − 1 • Hai hàm số y = và y =
không xác định trên R nên loại. x + 3 x − 2
• Hàm số y = x3 + x có đạo hàm y0 = 3x2 + 1 > 0 với mọi x ∈ R nên đồng biến trên R.
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 6. Hỏi hàm số y = x4 − 2x2 + 3 đồng biến trên khoảng nào? A. R.
B. (−∞; −1) và (0; 1).
C. (−1; 0) và (1; +∞).
D. (−1; 0) và (0; 1). Lời giải. "x = 0
Ta có y0 = 4x3 − 4x ⇒ y0 = 0 ⇔ x = ±1. Bảng xét dấu x −∞ −1 0 1 +∞ y0 − 0 + 0 − 0 +
Từ bảng xét dấu ta thấy hàm số đồng biến trên khoảng (−1; 0) và (1; +∞).
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 2
Câu 7. Hàm số y = x4 − 2 nghịch biến trên khoảng nào dưới đây? 1 1 A. −∞; . B. (0; +∞). C. ; +∞ . D. (−∞; 0). 2 2 Lời giải.
Ta có y0 = 4x3. Cho y0 = 0 ⇔ x = 0. Bảng biến thiên x −∞ 0 +∞ y0 − 0 + +∞ +∞ y −2
Dựa vào bảng biến thiên suy ra hàm số nghịch biến trên khoảng (−∞; 0).
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 8. Hàm số y = −x4 + 2x3 − 2x − 1 nghịch biến trên khoảng nào sau đây? 1 1 A. −∞; − . B. − ; +∞ . C. (−∞; +∞). D. (−∞; 1). 2 2 Lời giải.
Tập xác định của hàm số là D = R. 1 x = −
y0 = −4x3 + 6x2 − 2, y0 = 0 ⇔ 2 . x = 1 Bảng xét dấu f 0(x) 1 x −∞ − 1 +∞ 2 f 0(x) + 0 − 0 − 1
Từ bảng xét dấu f 0(x) suy ra hàm số nghịch biến trên khoảng − ; +∞ . 2
Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2x + 5
Câu 9. Cho hàm số y =
. Tìm mệnh đề đúng trong các mệnh đề sau x − 2
A. Hàm số nghịch biến trên khoảng (−∞; 3).
B. Hàm số nghịch biến trên (−∞; −2) ∪ (−2; +∞).
C. Hàm số nghịch biến trên R \ {2}.
D. Hàm số nghịch biến trên các khoảng (−∞; 2) và (2; +∞). Lời giải. TXĐ: D = R \ {2}. −9 Ta có y0 = < 0, với ∀x ∈ D. (x − 2)2
Suy ra hàm số nghịch biến trên các khoảng (−∞; 2) và (2; +∞).
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2x + 1
Câu 10. Cho hàm số y = . Mệnh đề đúng là x + 1
A. Hàm số đồng biến trên các khoảng (−∞; −1) và (−1; +∞), nghịch biến trên (−1; 1).
B. Hàm số đồng biến trên tập R.
C. Hàm số đồng biến trên các khoảng (−∞; −1) và (−1; +∞).
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 3
D. Hàm số nghịch biến trên các khoảng (−∞; −1) và (−1; +∞). Lời giải. 1 Ta có y0 = > 0,
∀x ∈ (−∞; −1) ∪ (−1; +∞). (x + 1)2
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 11. Trong 8 phút kể từ khi xuất phát, độ cao h (tính bằng mét) của khinh khí cầu vào tời
điểm t phút được cho bởi công thức h(t) = 6t3 − 81t2 + 324t. Hỏi độ cao của khinh khí cầu
giảm trong khoảng thời gian nào?
A. Từ phút thứ 2 đến phút thứ 6.
B. Từ phút thứ 3 đến phút thứ 6.
C. Từ phút thứ 4 đến phút thứ 8.
D. Từ phút thứ 6 đến phút thứ 8. Lời giải.
Ta có h0(t) = 18t2 − 162t + 324; "t = 3
h0(t) = 0 ⇔ 18t2 − 162t + 324 = 0 ⇔ Bảng biến thiên: t = 6. t 0 3 6 8 h0(t) + 0 − 0 + 480 405 h(t) 324 0
Dựa vào bảng biến thiên ta thấy khinh khí cầu giảm dần độ cao trong khoảng thời gian từ
phút thứ 3 đến phút thứ 6.
Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 12. ax + b
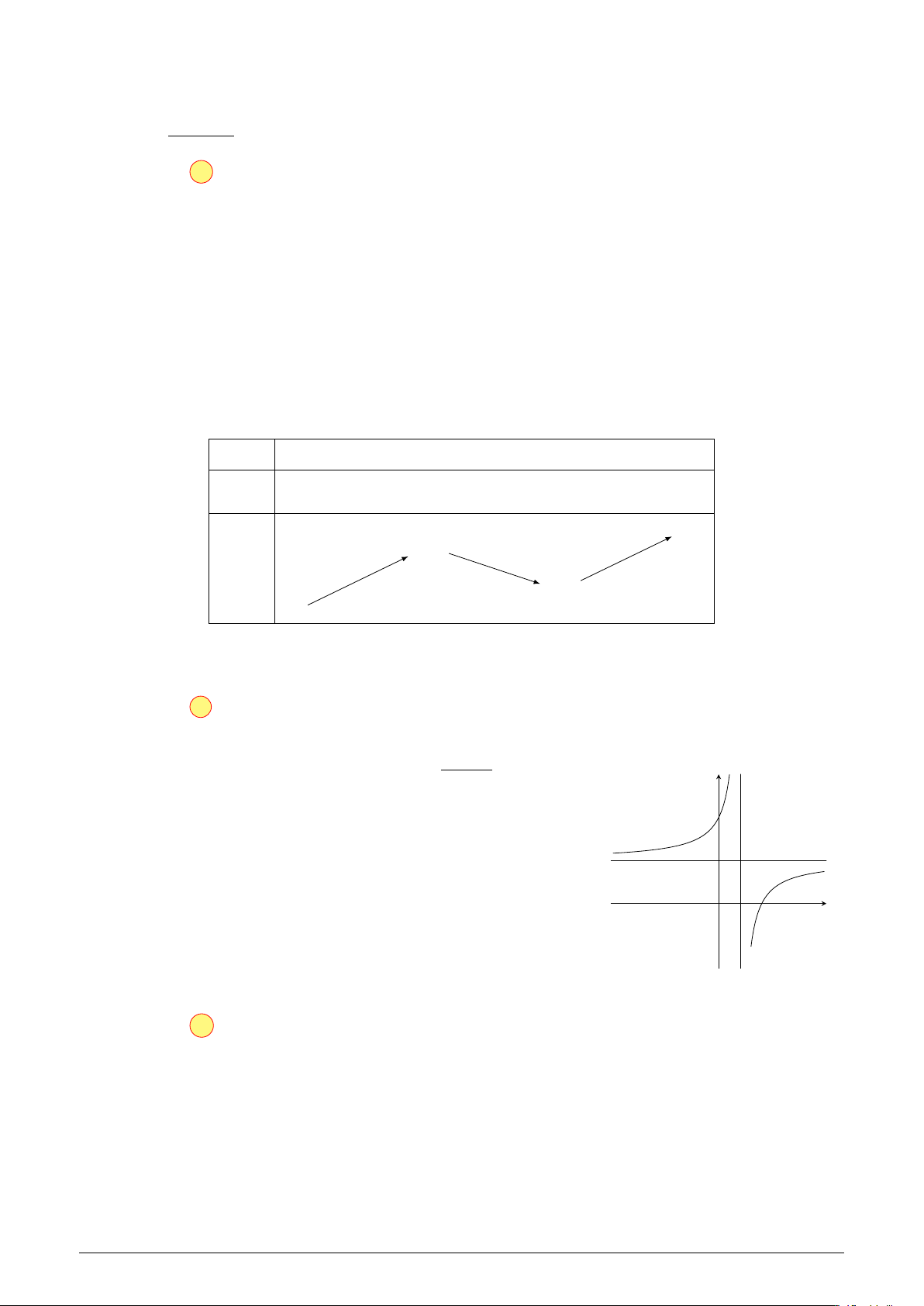
Đường cong ở hình bên là đồ thị hàm số y = , với a, b, c, d y cx + d
là các số thực. Mệnh đề nào dưới đây là đúng?
A. y0 < 0, ∀x 6= 1.
B. y0 < 0, ∀x 6= 2.
C. y0 > 0, ∀x 6= 2.
D. y0 > 0, ∀x 6= 1. 2 O x 1 Lời giải.
Từ đồ thị ta thấy hàm số tăng trên mỗi khoảng (−∞; 1) và (1; +∞) nên y0 > 0, ∀x 6= 1.
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 13. Tìm giá trị cực tiểu yCT của hàm số y = −x3 + 3x − 4. A. yCT = −1. B. yCT = −2. C. yCT = 1. D. yCT = −6. Lời giải.
Tập xác định: D = R. Ta có: y0 = −3x2 + 3. y0 = 0 ⇔ x = ±1. Bảng biến thiên
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 4 x −∞ −1 1 +∞ y0 − 0 + 0 − +∞ −2 y −6 −∞
Vậy yCĐ = y(1) = −2; yCT = y (−1) = −6.
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 14. Cho hàm số y = 7x3 + 9x2 − 3x − 4. Khẳng định nào sau đây là sai? 1
A. Giá trị cực đại y = 1.
B. Hàm số đạt cực tiểu tại x = . 7 1
C. Giá trị cực tiểu y = .
D. Hàm số đạt cực đại tại x = −1. 7 Lời giải. Tập xác định R. y0 = 21x2 + 18x − 3. 1
y0 = 0 ⇔ x = −1 hoặc x = . 7
Do đó, hàm số đạt cực đại tại x = −1, yCĐ = 1. 1 207
Hàm số đạt cực tiểu tại x = , y . 7 CT = − 49
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 15. Gọi A, B là hai điểm cực trị của đồ thị hàm số y = x3 − 3x2 + 4. Tính diện tích S của
tam giác OAB với O là gốc tọa độ.√ A. S = 8. B. S = 3. C. S = 2. D. S = 4. Lời giải.
Ta có y0 = 3x2 − 6x và y0 = 0 ⇔ x = 0 hoặc x = 2.
Do đó hai điểm cực trị của đồ thị hàm số là A(0; 4), B(2; 0). 1
Diện tích tam giác vuông OAB là SOAB = OA · OB = 4. 2
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 16. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số y = x3 − 3x2 + 4 bằng √ √ A. 2 2. B. 2 5. C. 4. D. 2. Lời giải. "x = 0 ⇒ y = 4
Ta có y0 = 3x2 − 6x, y0 = 0 ⇒ x = 2 ⇒ y = 0.
Suy ra hai điểm cực trị của đồ thị hàm số là A(0; 4), B(2; 0). √
Do đó AB = p22 + (−4)2 = 2 5.
Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 17. Đồ thị của hàm số y = x3 − 3x2 − 9x + 1 có hai điểm cực trị A và B. Điểm nào dưới
đây thuộc đường thẳng AB? A. N(1; −10). B. Q(−1; 10). C. M(0; −1). D. P(1; 0). Lời giải. "x = −1
y0 = 3x2 − 6x − 9; y0 = 0 ⇔ x = 3.
Với x = −1 ⇒ y = 6; x = 3 ⇒ y = −26.
Gọi A(−1; 6), B(3; −26) là hai điểm cực trị của đồ thị hàm số.
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 5 x + 1 y − 6
⇒ phương trình đường thẳng AB : = hay AB : 8x + y + 2 = 0. 4 −32
Ta có 8 · 1 + (−10) + 2 = 0 nên N ∈ AB.
Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 18. Cho hàm số y = f (x) có tập xác định [−8; 8]\{2} và có bảng biến thiên như hình bên
dưới. Khẳng định nào sau đây là khẳng định đúng? x −8 −1 2 4 8 y0 + 0 + + 0 − +∞ 3 y 1 −2 −∞ −∞
A. Điểm cực tiểu của đồ thị là (−8; −2).
B. Hàm số đồng biến trên khoảng (−8; 2).
C. Hàm số đạt cực trị tại x = −1.
D. Hàm số đồng biến trên khoảng (−1; 4). Lời giải.
Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 19.
Cho hàm số có đồ thị như hình bên. Khẳng định nào sai? 3 y 3 3 −
A. Hàm số có một cực tiểu tại x =
và đạt cực đại tại x = 0. 4 4 4 x O 113 −1
B. Giá trị cực đại y = −1 và giá trị cực tiểu y = − . 32 3
C. Hàm số có một cực tiểu tại x = − . 4 3
D. Hàm số có một cực đại tại x = − . 4 113 − 32 Lời giải.
Dựa vào đồ thị ta thấy, hàm số đạt cực đại tại x = 0, yCĐ = −1. 3 3 113
Hàm số đạt cực tiểu tại x = − và x = , y . 4 4 CT = − 32
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 20. Cho hàm số y = f (x) liên tục trên R và có f 0(x) = x3(x − 2019)2(x − 2020). Tìm số
cực trị của hàm số y = f (x). A. 4. B. 3. C. 1. D. 2. Lời giải. x = 0
Ta có f 0(x) = 0 ⇔ x = 2019 x = 2020.
Bảng xét dấu của đạo hàm x −∞ 0 2019 2020 +∞ f 0(x) + 0 − 0 − 0 +
Từ bảng xét dấu suy ra hàm số có đúng 2 cực trị.
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 6 Câu 21.
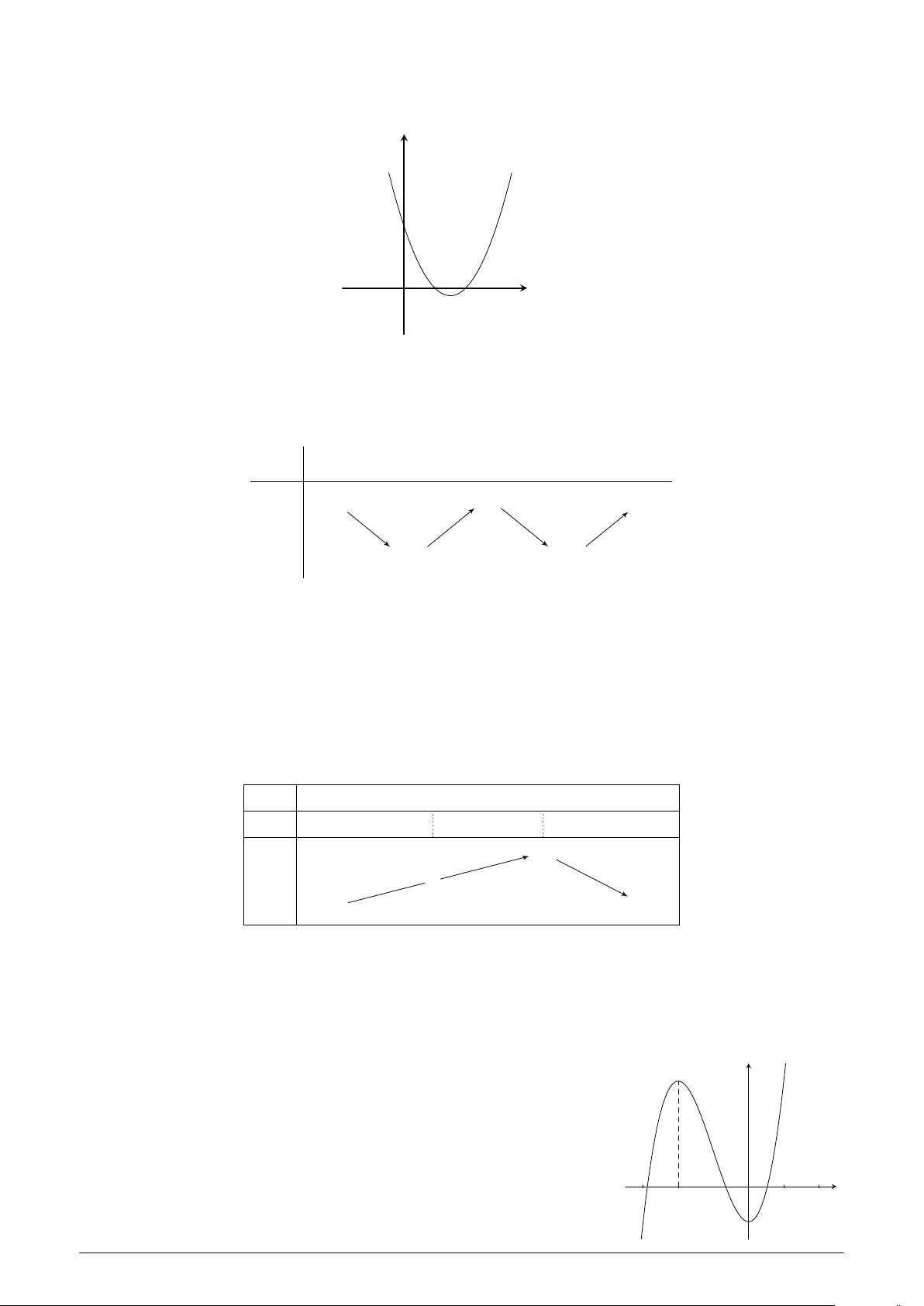
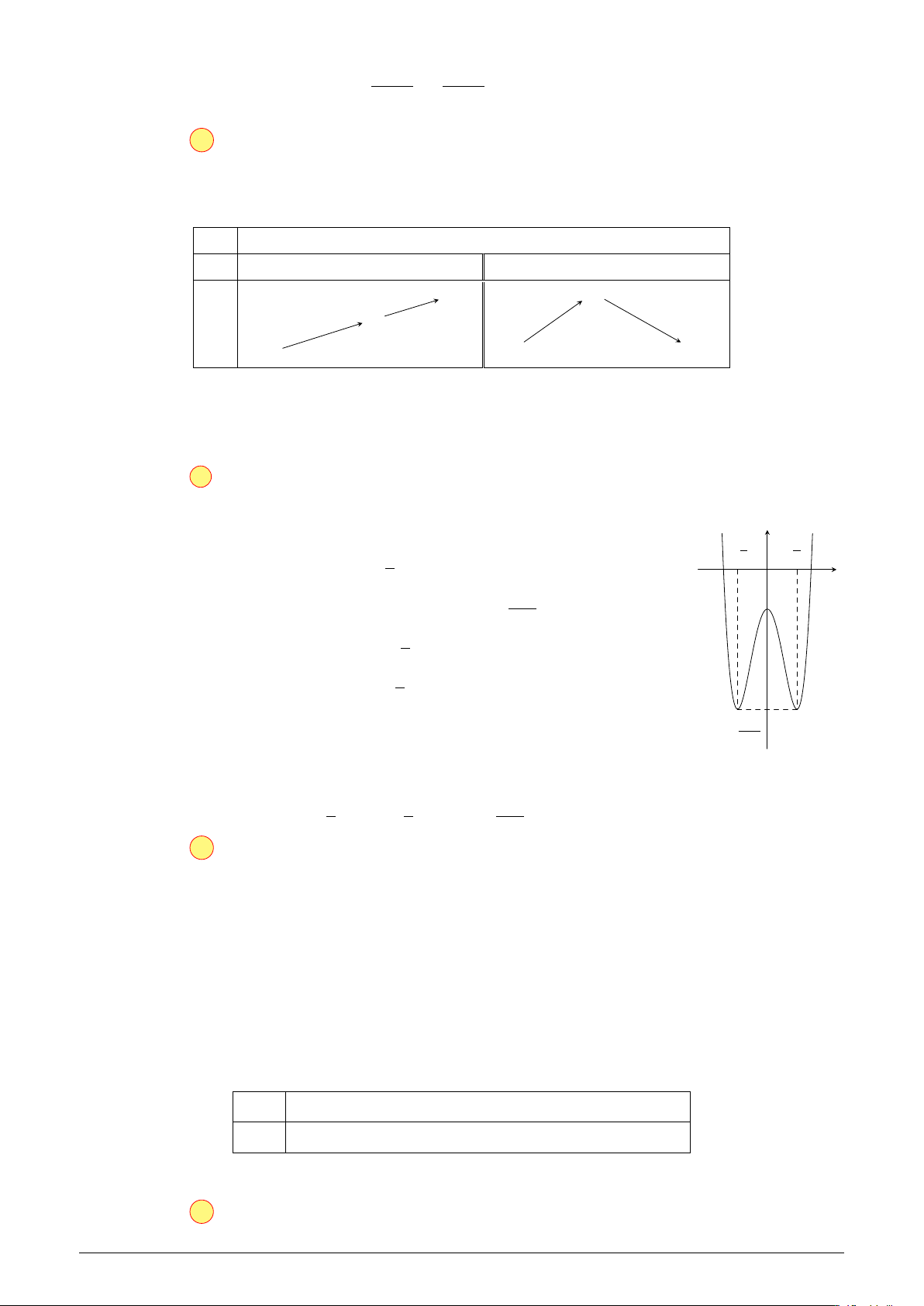
Cho hàm số f (x) có đạo hàm trên R là hàm số f 0(x). Biết đồ thị của y
hàm số f 0(x) được cho như hình vẽ. Hàm số y = f (x) nghịch biến trên khoảng nào sau đây? A. (−∞; −3). B. (0; 1). C. (−3; −2). D. (−∞; −1). O − x 3 −2 1 Lời giải.
Ta có f 0(x) < 0 ⇔ x ∈ (−3; −2) nên hàm số nghịch biến trên (−3; −2).
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 22.
Cho hàm đa thức bậc năm y = f (x). Đồ thị hàm số y = f 0(x) như y
hình vẽ. Hàm số y = f (x) có bao nhiêu điểm cực tiểu? A. 4. B. 2. O 1 3 C. 3. D. 1. x Lời giải.
Từ đồ thị, ta có bảng biến thiên x −∞ 0 1 3 +∞ y0 + 0 − 0 − 0 + y
Từ bảng biến thiên, ta thấy hàm số có 1 điểm cực tiểu.
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 Câu 23. Hàm số y =
x3 + (m + 1)x2 − (m + 1)x + 1 đồng biến trên tập xác định của nó khi 3 và chỉ khi A. −2 < m < 1. B. −2 ≤ m ≤ −1.
C. −2 < m < −1. D. −1 ≤ m ≤ 2. Lời giải. Tập xác định R.
Ta có y0 = x2 + 2(m + 1)x − (m + 1).
Hàm số đồng biến trên tập xác định của nó khi y0 ≥ 0 với mọi x ∈ R
hay y0 = x2 + 2(m + 1)x − (m + 1) ≥ 0(1) với mọi x ∈ R.
Ta có ∆0 = (m + 1) · (m + 2) khi đó (1) ⇔ ∆0 ≤ 0 ⇔ (m + 1) · (m + 2) ≤ 0 ⇔ −2 ≤ m ≤ −1. Vậy −2 ≤ m ≤ −1.
Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
Câu 24. Tìm tất cả các giá trị thực của tham số m để hàm số y = − x3 − mx2 + (2m − 3)x − 3
m + 2 nghịch biến trên R. A. m ≤ −3, m ≥ 1. B. −3 < m < 1. C. −3 ≤ m ≤ 1. D. m ≤ 1. Lời giải.
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 7
Ta có y0 = −x2 − 2mx + (2m − 3).
Hàm số nghịch biến trên R khi y0 ≤ 0 ( a = −1 < 0 ⇔ ∆0 ≤ 0 ⇔ m2 + 2m − 3 ≤ 0 ⇔ − 3 ≤ m ≤ 1.
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 25. Cho hàm số f (x) = x3 − 3(m + 1)x2 + 3m(m + 2)x. Có bao nhiêu giá trị nguyên của
tham số thực m để hàm số nghịch biến trên khoảng (0; 1)? A. 0. B. 1. C. 2. D. Vô số. Lời giải. "x = m
Đạo hàm: f 0(x) = 3 x2 − 2(m + 1)x + m(m + 2); y0 = 0 ⇔ x = m + 2. Bảng biến thiên x −∞ m m + 2 +∞ y0 + 0 − 0 + f (m) +∞ y −∞ f (m + 2) (m ≤ 0
Dựa vào BBT, ta có YCBT ⇔ (0; 1) ⊂ [m; m + 2] ⇔ ⇔ −1 ≤ m ≤ 0. m + 2 ≥ 1
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x + m2
Câu 26. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = đồng biến trên x + 4
từng khoảng xác định của nó? A. 5. B. 1. C. 3. D. 2. Lời giải. 4 − m2 Ta có y0 = . (x + 4)2
Để hàm số đồng biến trên các khoảng xác định thì 4 − m2 > 0 ⇔ −2 < m < 2.
Vậy có 3 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . x + 2 − m
Câu 27. Tìm tất cả các giá trị thực của tham số m để hàm số y = nghịch biến trên x + 1
các khoảng mà nó xác định? A. m < −3. B. m ≤ 1. C. m < 1. D. m ≤ −3. Lời giải.
Tập xác định D = R\ {−1} . m − 1 Có y0 = . (x + 1)2 m − 1
Hàm số nghịch bến trên mỗi khoảng của tập xác định ⇔
< 0, ∀x ∈ D ⇔ m < 1. (x + 1)2
Chọn đáp án C . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 8 x − 1
Câu 28. (TN.2017-2018). Tìm tất cả các giá trị thực của tham số m để hàm số y = nghịch x − m
biến trên khoảng (−∞; 2). A. m > 1. B. m ≥ 1. C. m > 2. D. m ≥ 2. Lời giải. −m + 1 Đạo hàm: y0 =
. Với −m + 1 < 0 ⇔ m > 1 thì y0 < 0, ∀x 6= m ⇒ hàm số đã cho (x − m)2
nghịch biến trên từng khoảng (−∞; m) và (m; +∞). YCBT ⇔ (−∞; 2) ⊂ (−∞; m) ⇔ m ≥ 2: (thỏa mãn).
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 29. Tìm tất cả các giá trị thực của m để hàm số y = x3 − 3x2 + (m + 1)x + 2 có hai điểm cực trị. A. m < 2. B. m ≤ 2. C. m > 2. D. m < −4. Lời giải.
y0 = 3x2 − 6x + m + 1, ∆0 = 6 − 3m.
Để hàm số có hai điểm cực trị thì y0 = 0 phải có hai nghiệm phân biệt tức là ∆0 > 0 ⇔ m < 2.
Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 30. Cho hàm số y = 2x3 + 3(m − 1)x2 + 6(m − 2)x − 18. Tập hợp tất cả các giá trị của
tham số m để hàm số có hai điểm cực trị thuộc khoảng (−5; 5) là
A. (−∞; −3) ∪ (7; +∞). B. (−3; +∞) \ {3}. C. (−∞; 7) \ {3}. D. (−3; 7) \ {3}. Lời giải.
y0 = 6x2 + 6(m − 1)x + 6(m − 2). "x1 = −1 ∈ (−5; 5)
y0 = 0 ⇔ x2 + (m − 1)x + (m − 2) = 0 ⇔ x2 = −m + 2. ( − ( m + 2 6= −1 m 6= 3
Hàm số có hai điểm cực trị thuộc khoảng (−5; 5) ⇔ ⇔ − 5 < −m + 2 < 5 − 3 < m < 7.
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 31. Cho hàm số y = (m + 1)x4 − mx2 + 3. Tìm tất cả các giá trị thực của tham số m để
hàm số có ba điểm cực trị.
A. m ∈ (−∞; −1) ∪ [0; +∞). B. m ∈ (−1; 0).
C. m ∈ (−∞; −1] ∪ [0; +∞).
D. m ∈ (−∞; −1) ∪ (0; +∞). Lời giải.
y0 = 4(m + 1)x3 − 2mx = 2x[2(m + 1)x2 − m] "x = 0
y0 = 0 ⇔ 2(m + 1)x2 − m = 0 (∗)
Hàm số có ba điểm cực trị khi phương trình (∗) có hai nghiệm phân biệt khác 0 " m m < −1 ⇔ > 0 ⇔ m + 1 m > 0.
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 32. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x4 + 2 m2 − m − 6 x2 +
m − 1 có 3 điểm cực trị? A. 5. B. 4. C. 3. D. 6. Lời giải.
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 9
Ta có y0 = 4x3 + 4(m2 − m − 6)x, ∀x ∈ R.
y0 = 0 ⇔ x = 0 hoặc x2 = −m2 + m + 6.
Hàm số đã cho có 3 điểm cực trị khi và chỉ khi phương trình x2 = −m2 + m + 6 có 2 nghiệm
phân biệt đôi một khác 0 ⇔ −m2 + m + 6 > 0 ⇔ −2 < m < 3.
Do m là số nguyên nên m ∈ {−1, 0, 1, 2}.
Chọn đáp án B . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 33. Cho hàm số f (x) có đạo hàm trên R và có dấu của f 0(x) như sau x −∞ −1 1 2 3 +∞ f 0(x) + 0 − 0 − 0 + 0 −
Hàm số y = f (2 − 3x) nghịch biến trên khoảng 1 1 1 1 1 A. − ; 0 . B. 0; . C. − ; . D. − ; 0 . 4 4 3 3 2 Lời giải. Đặt g(x) = f (2 − 3x).
Ta có g0(x) = −3 f 0(2 − 3x). 1 x = − 3 x = 0 Ta thấy g0(x) = 0 ⇔ . Ta có bảng biến thiên 1 x = 3 x = 1 1 1 x −∞ − 0 1 +∞ 3 3 g0(x) + 0 − 0 + 0 + 0 − 1
Từ bảng biến thiên, ta thấy hàm số g(x) nghịch biến trên − ; 0 . 4
Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 34. Cho hàm số y = f (x) liên tục và có đạo hàm trên R. Hàm số y = f 0(x) có đồ thị như hình bên dưới. y y = f 0(x) 2 x O 1 2
Hàm số g(x) = f 1 + 2x − x2 đồng biến trên khoảng nào dưới đây? A. (1; 2). B. (0; 1). C. (−∞; 1). D. (1; +∞). Lời giải.
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 10
Ta có g0(x) = (2 − 2x) f 0 1 + 2x − x2. g0(x) = 0 2 − 2x = 0 ⇔ f0 1 + 2x − x2 = 0 x = 1 ⇔ 1 + 2x − x2 = 1 1 + 2x − x2 = 2 x = 1 ⇔ x = 0 x = 2. Bảng xét dấu của g0(x). x −∞ 0 1 2 +∞ g0(x) + 0 − 0 + 0 −
Từ bảng biến thiên ta thấy, hàm số g(x) đồng biến trên (−∞; 0); (1; 2).
Chọn đáp án A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 35. (TN.2019). Cho hàm số f (x), bảng biến thiên của hàm số f 0(x) như hình vẽ bên dưới x −∞ −1 0 1 +∞ +∞ 2 +∞ f 0(x) −3 −1
Số điểm cực trị của hàm số y = f (x2 + 2x) là A. 3. B. 9. C. 5. D. 7. Lời giải. 2x + 2 = 0 x2 + 2x = a, a < −1
Ta có y0 = (2x + 2) f 0 x2 + 2x = 0 ⇔ x2 + 2x = b, − 1 < b < 0 x2 + 2x = c, 0 < c < 1 x2 + 2x = d, d > 1.
Xét hàm số g(x) = x2 + 2x xác định trên R, có y0 = 2x + 2, ta có bảng biến thiên như hình vẽ. x −∞ −1 +∞ g0(x) − 0 + +∞ +∞ g(x) −1
Dựa vào bảng biến thiên ta được y0 = 0 có 7 nghiệm đơn nên hàm số đã cho có 7 điểm cực trị.
Chọn đáp án D . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 11
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số y = f (x) có bảng biến thiên như sau x −∞ 0 1 +∞ y0 + 0 + 0 − 2 y 0 −∞ −∞
Xét tính đúng sai của các khẳng định sau:
a) Hàm số đồng biến trên (−∞; 2).
b) Hàm số nghịch biến trên (1; +∞).
c) Hàm số có hai điểm cực trị.
d) Hàm số đạt cực đại tại x = 1. Lời giải.
Quan sát bảng biến thiên, ta có các kết quả sau:
a) Hàm số đồng biến trên (−∞; 1) nên khẳng định hàm số đồng biến trên (−∞; 2) là sai.
b) Hàm số nghịch biến trên (1; +∞).
c) Hàm số có đúng 1 điểm cực trị là x = 1.
d) Hàm số có đạt cực đại tại x = 1.
Chọn đáp án a sai b đúng c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . Câu 2.
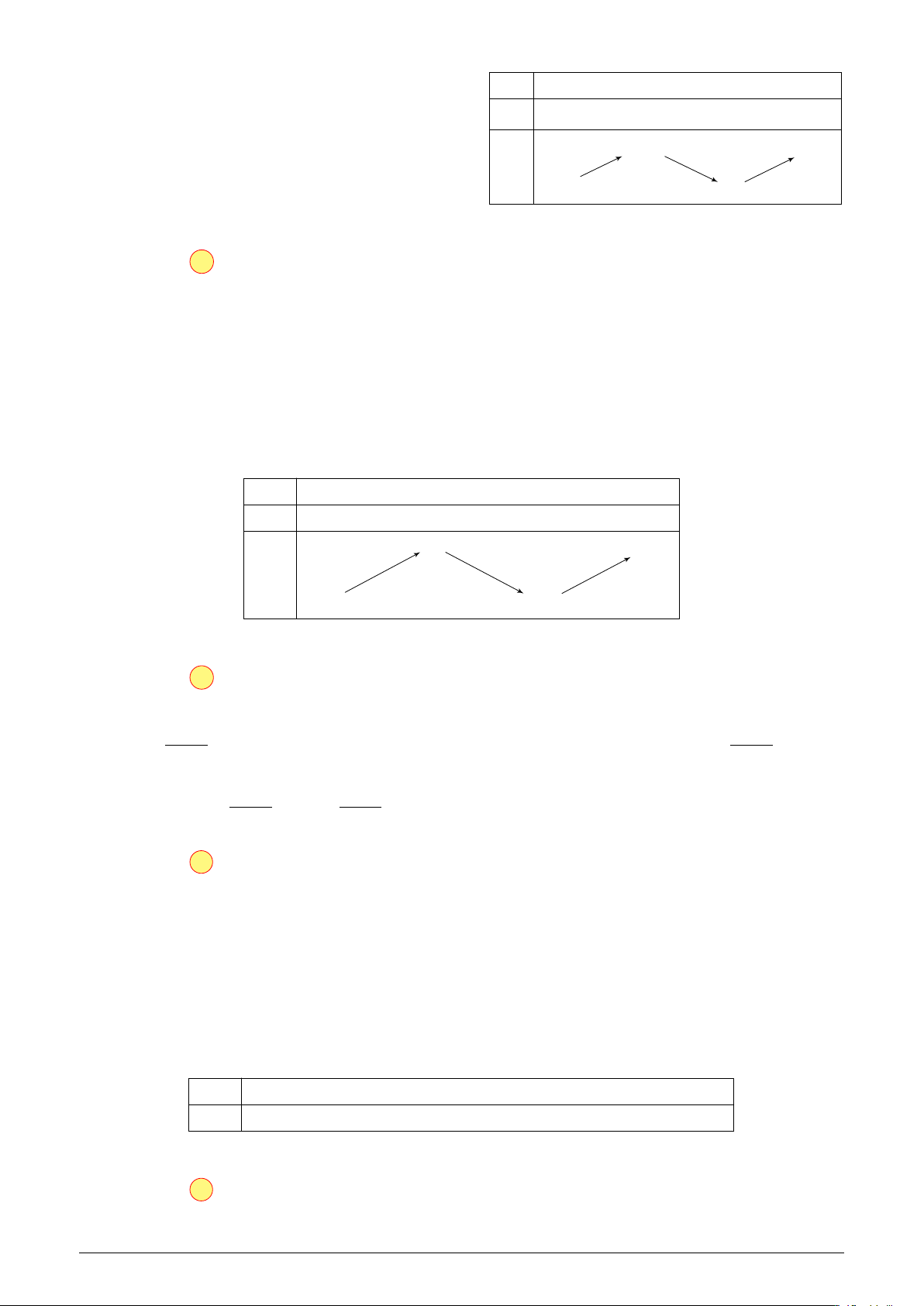
Cho hàm số y = f (x) có đồ thì như hình vẽ bên. Xét tính đúng y
sai của các khẳng định sau:
a) Hàm số đã cho nghịch biến trên khoảng (−2, 0).
b) Hàm số đã cho đồng biến trên khoảng (−1; +∞).
c) Hàm số đã cho đồng biến trên khoảng (2; +∞). O x
d) Hàm số đạt cực tiểu tại x = −1. −3 −2 1 2 −1 Lời giải.
Nếu không quen nhìn đồ thị, ta có thể từ đồ thị thiết lập lại bảng biến thiên như sau: x −∞ −2 0 +∞ y0 + 0 − 0 + +∞ y −∞ −1 Suy ra
a) Hàm số nghịch biến trên khoảng (−2, 0).
b) Hàm số đồng biến trên khoảng (0; +∞) nên khẳng định đồng biến trên khoảng (−1; +∞) là sai.
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 12
c) Hàm số đồng biến trên khoảng (0; +∞) nên nên hàm số đồng biến trên khoảng (2; +∞).
d) Hàm số đạt cực tiểu tại x = 0 (chú ý y = −1 gọi là giá trị cực tiểu).
Chọn đáp án a đúng b sai c đúng d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 3. Cho hàm số y = f (x) xác định trên R và có đạo hàm f 0(x) = 3x3 − 3x2, ∀x ∈ R. Xét
tính đúng sai của các khẳng định sau:
a) Hàm số đồng biến trên khoảng (1; +∞).
b) Hàm số nghịch biến trên khoảng (−1; 1).
c) Đồ thị hàm số có hai điểm cực trị.
d) Đồ thị hàm số có một điểm cực tiểu. Lời giải. "x = 0
Ta có: y0 = 0 ⇔ 3x3 − 3x2 = 0 ⇔ x = 1. Bảng biến thiên: x −∞ 0 1 +∞ y0 − 0 − 0 + +∞ +∞ y CT Suy ra
a) Hàm số đồng biến trên khoảng (1; +∞).
b) Hàm số nghịch biến trên khoảng (−∞; 1) nên nghịch biến trên (−1; 1).
c) Hàm số có đúng một điểm cực trị.
d) Hàm số có đúng một điểm cực tiểu x = 1.
Chọn đáp án a đúng b đúng c sai d đúng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 4. Cho hàm số y = f (x) = x4 − 2x2 − 3. Xét tính đúng sai của các khẳng định sau:
a) Hàm số đã cho đạt cực đại tại x = 0.
b) Hàm số đã cho đạt cực tiểu tại x = −3.
c) Hàm số đã cho có giá trị cực đại và cực tiểu lần lượt là −4, −3.
d) Đồ thị hàm số g(x) = f (x) + 3 có điểm cực đại là (0; 0) . Lời giải.
Ta có y0 = 4x3 − 4x. Giải y0 = 0 ta được x = −1, x = 0, x = 1. Bảng biến thiên x −∞ −1 0 1 +∞ y0 − 0 + 0 − 0 + −∞ −3 +∞ y −9 1
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 13
a) Dựa vào bảng biến thiên ta thấy hàm số đạt cực đại tại x = 0
b) Dựa vào bảng biến thiên ta thấy hàm số đạt cực tiểu tại x = −3
c) Dựa vào bảng biến thiên ta thấy hàm số giá trị cực đại và cực tiểu lần lượt là −4, −3
d) Dựa vào bảng biến thiên ta thấy hàm số g(x) = f (x) + 3 có được bằng cách tịnh tiến đồ
thị y = f (x) lên trên 3 đơn vị. Suy ra đồ thị hàm số g(x) = f (x) + 3 có điểm cực đại là (0; 0).
Chọn đáp án a đúng b sai c sai d sai . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Câu 1. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số y = −x3 + 3x + 2 bằng bao nhiêu?
(kết quả làm tròn đến hàng phần trăm) Lời giải.
? Tập xác định D = R. ? Đạo hàm y0 = −3x2 + 3. "x = −1 ⇒ y = 0 ? y0 = 0 ⇔ x = 1 ⇒ y = 4 ? Bảng biến thiên x −∞ −1 1 +∞ y0 − 0 + 0 − +∞ 4 y 0 −∞
? Hàm số đạt cực đại tại x = 1, yCĐ = 4, suy ra A(1; 4).
? Hàm số đạt cực tiểu tại x = −1, yCT = 0, suy ra B(−1; 0).
? Khoảng cách giữa hai điểm cực trị của đồ thị hàm số là AB = p(1 + 1)2 + (4 − 0)2 = √ 2 5 ≈ 4,47.
Đáp án: 4,47 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
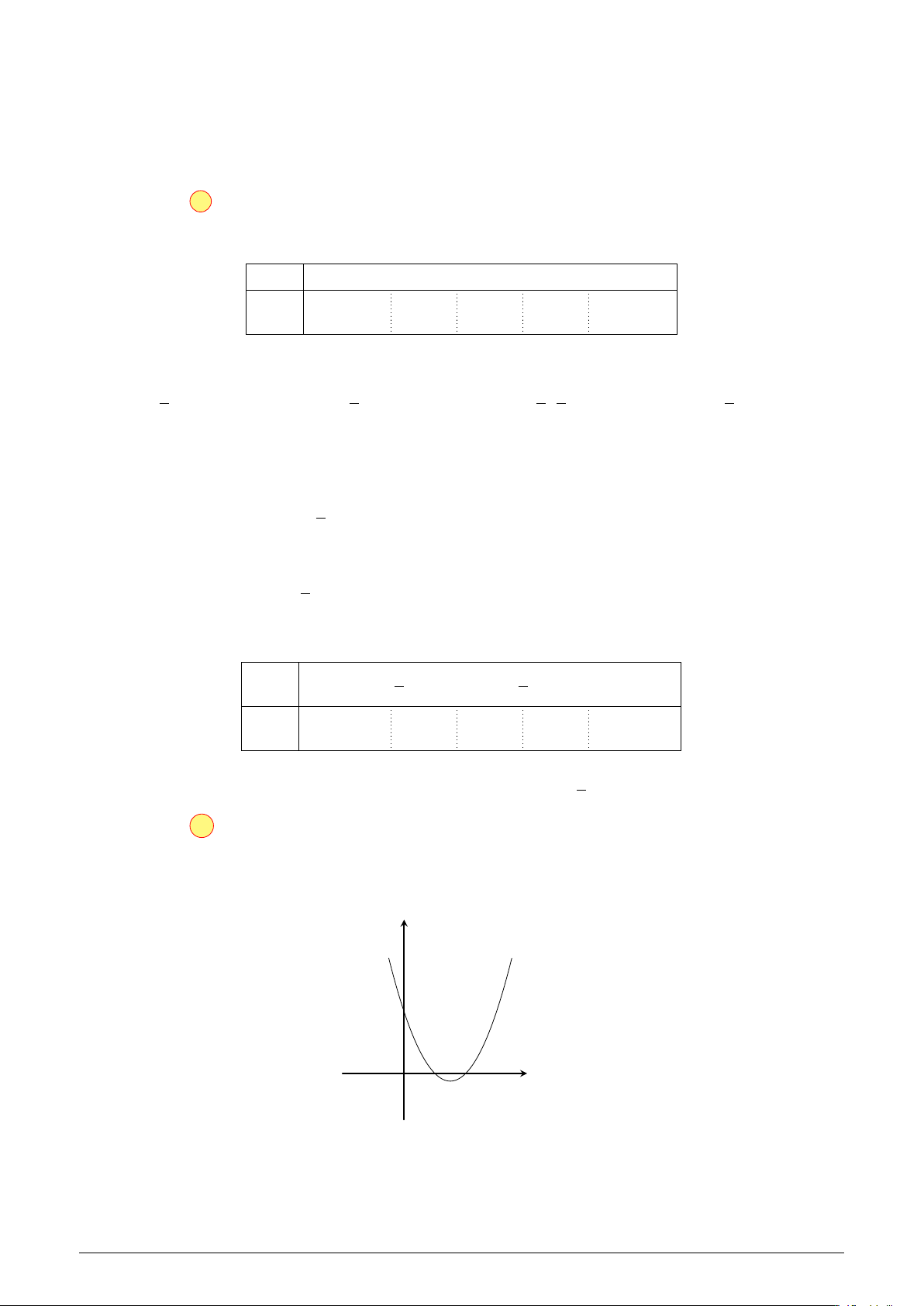
Câu 2. Cho hàm số y = x4 − 8x2 + 10 có đồ thị (C). Gọi A, B, C là ba điểm cực trị của đồ thị
(C). Tính diện tích S của tam giác ABC. Lời giải. "x = 0
Ta có y0 = 4x3 − 16x, y0 = 0 ⇔ . x = ±2
Tọa độ 3 điểm cực trị của đồ thị hàm số là A(0; 10), B(−2; −6), C(2; −6).
Gọi H là trung điểm BC ⇒ H(0; −6).
Theo tính chất của hàm trùng phương nên tam giác ABC cân tại A. 1 1
Do đó SABC = AH · BC = 16 · 4 = 32. 2 2
Đáp án: 32 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Chương I. Ứng dụng đạo hàm để khảo sát hàm số Trang 14