Đề KT Toán 11 giữa học kỳ 2 năm học 2020-2021 (có đáp án)

SỞ GIÁO DỤC & ĐÀO TẠO
ĐỀ KIỂM TRA GIỮA HỌC KỲ II
MÔN: TOÁN KHỐI 11 NĂM HỌC 2020-2021 MÃ ĐỀ: 001
Thời gian làm bài: 60 phút;
(21 câu trắc nghiệm)
(Thí sinh không được sử dụng tài liệu)
Họ, tên thí sinh:..................................................................... SBD: .............................
I. PHẦN TRẮC NGHIỆM (7 điểm): ì x - 2 ï khi x ¹ 4 ï Câu 1: Cho hàm số x - 4 f (x) = í
. Khẳng định nào sau đây đúng? 1 ï khi x = 4 ïî4
A. Hàm số liên tục tại mọi điểm trên tập xác định nhưng gián đoạn tại x = 4 .
B. Hàm số liên tục tại x = 4 .
C. Hàm số không liên tục tại x = 4 .
D. Hàm số liên tục trên ! . +
Câu 2: Tính giới hạn 3 2x lim . x® 2- - x + 2 A. 3 2 . B. . C. +¥ . D. -¥ . 2
Câu 3: Mệnh đề nào sau đây là đúng?
A. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
C. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.
D. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
Câu 4: Mệnh đề nào sau đây là đúng? 3 - 3 1 2 - n A. lim = . B. lim = +¥ . C. lim = -¥ . D. lim( 2 - n + ) 1 = -¥ . 2 - n +1 2 n 2 3n
Câu 5: Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ . Mặt phẳng ( AB D
¢ ¢) song song với mặt phẳng nào trong các
mặt phẳng sau đây? A. (BCA¢). B. (BC D ¢ ).
C. ( A¢C C ¢ ). D. (BDA¢) .
Câu 6: Cho hình hộp ABC .
D A' B 'C ' D ' . Chọn khẳng định đúng. !!!" !!!" !!!" !!!!" !!!" !!!" !!!" !!!"
A. BA + BC + BB¢ = BC ' .
B. BA + BC + BB¢ = BD . !!!" !!!" !!!" !!!!" !!!" !!!" !!!" !!!"
C. BA + BC + BB¢ = BD '.
D. BA + BC + BB¢ = BA'
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, tam giác SAD vuông tại A và ∑ 0
ASD = 50 . Tính số đo của góc tạo bởi hai đường thẳng BC và . SD A. 0 50 . B. 0 20 . C. 0 30 . D. 0 40 .
Câu 8: Cho một đường thẳng a song song với mặt phẳng (P) . Có bao nhiêu mặt phẳng chứa a
và song song với (P) ? A. vô số. B. 0 . C. 2 . D. 1. Trang 1 2 x +1
Câu 9: Cho hàm số f (x) =
. Khi đó hàm số y = f (x) liên tục trên các khoảng nào sau 2 x + 5x + 6 đây? A. ( ; -¥ 2 - ). B. ( ;3 -¥ ) . C. ( 2; - +¥). D. ( 3; - 2). æ 1 1 1 1
Câu 10: Tìm giá trị đúng của ö S = 2 + + +!+ +! . ç n ÷ è 2 4 8 2 ø 1 A. 2 +1. B. 2 . C. 2 . D. . 2 2
ìx - 3 khi x ³ 2
Câu 11: Cho hàm số f (x) = í
. Chọn kết quả đúng của lim f (x).
îx -1 khi x < 2 x®2 A. 1. B. Không tồn tại. C. 1 - . D. 0 . 3x +1 -1 a a Câu 12: Biết lim
= , trong đó a , b là các số nguyên dương và phân số tối giản. x®0 x b b
Tính giá trị biểu thức 2 2
P = a + b . A. P = 40 . B. P = 5. C. P = 0 . D. P = 13. 4 2n - 2n + 2 lim bằng Câu 13: 4 4n + 2n + 5 1 2 A. 0 . B. . C. . D. +¥ . 2 11
Câu 14: Giả sử ta có lim f (x) = a và lim g (x) = b . Trong các mệnh đề sau, mệnh đề nào sai? x®+¥ x®+¥ f ( x) A. a lim = . B. lim é f
ë ( x).g ( x)ù = . a b . û
x®+¥ g ( x) b x®+¥ C. lim é f
ë ( x) - g ( x)ù = a - b .
D. lim é f x + g x ù = a + b . û ë ( ) ( )û x®+¥ x®+¥
Câu 15: Trong các công thức sau, công thức nào đúng ? ! ! ! ! ! ! ! ! ! ! ! ! A. . u v |
= u | . v .cos (u,v). B. .
u v = u.v .cos (u,v). ! ! ! ! ! ! ! ! ! ! ! ! C. . u v |
= u | . v .sin (u,v) . D. .
u v = u.v .sin (u,v). 2 n + Câu 16: Giới hạn 7 3 n a 3 a lim =
(với a,b là các số nguyên dương và là phân số tối 2(3n + 2) b b
giản). Tính T = a + b . A. T = 21. B. T = 7 . C. T = 9 . D. T = 13 . !!!"
Câu 17: Cho hình lập phương A .
BCD A'B'C'D' . Khi đó, vectơ bằng vectơ AB là vectơ nào dưới đây? !!!!!" !!!" !!!" !!!!!"
A. D'C' . B. BA. C. CD .
D. B' A' . x +1
Câu 18: Tìm giới hạn A = lim . 2 x 2 ®- x + x + 4 1 A. -¥ . B. 1. C. - . D. +¥ . 6
Câu 19: Phát biểu nào sau đây là sai ?
A. limu = c ( u = c là hằng số ). B. lim n q = 0 ( q > ) 1 . n n 1 C. lim = 1 0 . D. lim = 0 (k > ) 1 . n k n Trang 2 3x - 2 Câu 20: Cho lim
= a là một số thực. Khi đó giá trị của 2 a bằng x®+¥ x + 3 A. 1 B. 9 C. 3 D. 4 2 ì x -1 ï ne·u x ¹ 1
Câu 21: Giá trị của m sao cho hàm số f (x) = í x -1
liên tục tại điểm x = 1 là 3
ïî x -m ne·u x =1 A. 1 - . B. 5. C. 5 - . D. 1.
II. PHẦN TỰ LUẬN (3 điểm): ì2x + a khi x £ 2 ï
Bài 1: Cho hàm số f (x) = í x - 2
. Tìm tất cả các giá trị của tham số a để hàm khi x > 2 ïî x -1-1
số liên tục tại x = 2 . 2n - 3
Bài 2: Tính giới hạn sau: lim . 3n + 5
Bài 3: Cho tứ diện ABCD có AB = AC = AD = BC = BD = a và CD = a 3 . Gọi I là trung
điểm BD . Tính số đo góc giữa hai đường thẳng AI và BC .
---------------------------------------------------------- HẾT ----------
SỞ GIÁO DỤC & ĐÀO TẠO
ĐỀ KIỂM TRA GIỮA HỌC KỲ II
MÔN: TOÁN KHỐI 11 NĂM HỌC 2020-2021 MÃ ĐỀ: 002
Thời gian làm bài: 60 phút;
(21 câu trắc nghiệm)
(Thí sinh không được sử dụng tài liệu)
Họ, tên thí sinh:..................................................................... SBD: .............................
I. PHẦN TRẮC NGHIỆM (7 điểm): 4 3n - 2n + 2 Câu 1: lim bằng 4 9n + 2n + 5 2 1 1 A. . B. 0 . C. . D. . 5 3 2 5x +1 -1 a a Câu 2: Biết lim
= , trong đó a , b là các số nguyên dương và phân số tối giản. x®0 x b b
Tính giá trị biểu thức 2 2
P = a + b . A. P = 26 . B. P = 6 . C. P = 0 . D. P = 29 . 2
ìx +1 khi x ³ 3
Câu 3: Cho hàm số f ( x) = í
. Chọn kết quả đúng của lim f ( x).
îx +1 khi x < 3 x®3 A. 1 - . B. Không tồn tại. C. 1. D. 0 .
Câu 4: Mệnh đề nào sau đây là đúng? - - A. 4 n 1 5 5 lim = -¥ . B. lim = -¥ . C. lim = . D. lim(5n - ) 1 = +¥ . 2 3n n 7 - n +1 7 Trang 3 2 ì x - 4 ï ne·u x ¹ 2
Câu 5: Giá trị của m sao cho hàm số f ( x) = í x - 2
liên tục tại điểm x = 2 là
ïîx + m ne·u x = 2 A. 2 . B. 1 - . C. 5 - . D. 1.
Câu 6: Cho một điểm M không thuộc mặt phẳng (P) . Có bao nhiêu mặt phẳng chứa M và song
song với (P) ? A. 2 . B. vô số. C. 1. D. 0 . 2x -1 Câu 7: Cho lim
= a là một số thực. Khi đó giá trị của 2 a bằng x®+¥ x + 4 A. 1 B. 2 C. 3 D. 4
Câu 8: Mệnh đề nào sau đây là đúng?
A. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.
C. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.
D. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.
Câu 9: Phát biểu nào sau đây là sai ? 1 A. lim n q = 0 ( q < ) 1 . B. lim = 0 . n 1 C. lim = +¥ (k > ) 1 .
D. limu = c ( u = c là hằng số ). k n n n ì x - 3 ï khi x ¹ 9 ï Câu 10: Cho hàm số x - 9 f (x) = í
. Khẳng định nào sau đây đúng? 1 ï khi x = 9 ïî9
A. Hàm số liên tục tại mọi điểm trên tập xác định.
B. Hàm số gián đoạn tại x = 9 .
C. Hàm số liên tục tại x = 9 .
D. Hàm số liên tục trên ! . 5 + 2x
Câu 11: Tính giới hạn lim . x 2- ®- x + 2 A. 3 2 . B. -¥ . C. . D. +¥ . 2
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, tam giác SAD vuông tại A và ∑ 0
ASD = 20 . Tính số đo của góc tạo bởi hai đường thẳng BC và . SD A. 0 60 . B. 0 70 . C. 0 50 . D. 0 20 . !!!!!"
Câu 13: Cho hình hộp chữ nhật A .
BCD A'B'C'D' . Khi đó, vectơ bằng vectơ D'C' là vectơ nào dưới đây? !!!" !!!" !!!" !!!!!" A. BA. B. CD . C. AB .
D. B' A' . æ 1 1 1 1
Câu 14: Tìm giá trị đúng của ö S = 2 + + +!+ +! . ç n ÷ è 3 9 27 3 ø A. 1 3 . B. . C. 1. D. 2 . 3
Câu 15: Trong các công thức sau, công thức nào đúng ? Trang 4 ! ! ! ! ! ! ! ! ! ! ! ! A. .
u v = u.v .cos (u,v). B. . u v |
= u | . v .sin (u,v) . ! ! ! ! ! ! ! ! ! ! ! ! C. .
u v = u.v .sin (u,v). D. . u v |
= u | . v .cos (u,v).
Câu 16: Giả sử ta có lim f (x) = a và lim g (x) = b . Trong các mệnh đề sau, mệnh đề nào sai? x®+¥ x®+¥ A. lim é f
ë ( x) - g ( x)ù = a - b .
B. lim é f x .g x ù = . a b . û ë ( ) ( )û x®+¥ x®+¥ f ( x) C. a lim é f
ë ( x) + g ( x)ù = a + b . D. lim = . û x®+¥
x®+¥ g ( x) b
Câu 17: Cho hình hộp ABC . D A¢B C ¢ D
¢ ¢ . Mặt phẳng (BC D
¢ ) song song với mặt phẳng nào trong
các mặt phẳng sau đây?
A. ( A¢C C ¢ ). B. ( AB D ¢ ¢) . C. (BDA¢) . D. (BCA¢). x +
Câu 18: Tìm giới hạn 1 A = lim . 2
x®2 x + x + 4 A. 3 . B. 0 . C. 1. D. +¥ . 10
Câu 19: Cho hình hộp ABC .
D A' B 'C ' D ' . Chọn khẳng định đúng. !!!" !!!" !!!" !!!!" !!!" !!!" !!!" !!!"
A. AB + AA' + AD = AD ' .
B. AB + AA' + AD = AC . !!!" !!!" !!!" !!!!" !!!" !!!" !!!" !!!!"
C. AB + AA' + AD = AB '
D. AB + AA' + AD = AC '. 2 n + Câu 20: Giới hạn 9 5 n a 5 a lim =
(với a,b là các số nguyên dương và là phân số tối 4(2n + ) 1 b b
giản). Tính T = a + b . A. T = 17 . B. T = 21. C. T = 13 . D. T = 11. 2 x + 5
Câu 21: Cho hàm số f (x) =
. Khi đó hàm số y = f (x) liên tục trên các khoảng nào sau 2 x - 6x + 5 đây? A. ( ) ;1 -¥ . B. ( ;5 -¥ ) . C. (0;+¥). D. ( 1; - 5).
II. PHẦN TỰ LUẬN (3 điểm): 3 ì x + a khi x £ 3 ï
Bài 1: Cho hàm số f (x) = í x - 3
. Tìm tất cả các giá trị của tham số a để hàm số khi x > 3 ïî x +1-2
liên tục tại x = 3. 5n - 3
Bài 2: Tính giới hạn sau: lim . 2n + 7
Bài 3: Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a và BC = a 3 . Gọi I là trung
điểm AB . Tính góc giữa hai đường thẳng SI và AC .
---------------------------------------------------------- HẾT ---------- Trang 5 ĐÁP ÁN
I. PHẦN TRẮC NGHIỆM: Mã đề Câu Đáp án Mã đề Câu Đáp án 001 1 B 002 1 C 001 2 C 002 2 D 001 3 A 002 3 B 001 4 D 002 4 D 001 5 B 002 5 A 001 6 C 002 6 C 001 7 D 002 7 B 001 8 D 002 8 A 001 9 C 002 9 C 001 10 B 002 10 B 001 11 A 002 11 B 001 12 D 002 12 B 001 13 B 002 13 C 001 14 A 002 14 C 001 15 A 002 15 D 001 16 D 002 16 D 001 17 A 002 17 B 001 18 C 002 18 A 001 19 B 002 19 D 001 20 C 002 20 A 001 21 D 002 21 A Mã đề Câu Đáp án Mã đề Câu Đáp án 003 1 B 004 1 C 003 2 D 004 2 D 003 3 D 004 3 B 003 4 A 004 4 D 003 5 D 004 5 C 003 6 B 004 6 C 003 7 A 004 7 B 003 8 B 004 8 B 003 9 B 004 9 A 003 10 C 004 10 A 003 11 D 004 11 A 003 12 C 004 12 B 003 13 B 004 13 C 003 14 D 004 14 C 003 15 A 004 15 D 003 16 C 004 16 A 003 17 C 004 17 D 003 18 C 004 18 B 003 19 C 004 19 D 003 20 C 004 20 C 003 21 A 004 21 B Mã đề Câu Đáp án Mã đề Câu Đáp án Trang 6 005 1 A 006 1 D 005 2 B 006 2 B 005 3 D 006 3 A 005 4 D 006 4 B 005 5 B 006 5 A 005 6 C 006 6 B 005 7 B 006 7 C 005 8 B 006 8 D 005 9 D 006 9 D 005 10 A 006 10 C 005 11 C 006 11 A 005 12 A 006 12 D 005 13 A 006 13 A 005 14 B 006 14 C 005 15 C 006 15 B 005 16 B 006 16 C 005 17 D 006 17 A 005 18 C 006 18 B 005 19 D 006 19 D 005 20 C 006 20 C 005 21 B 006 21 A Mã đề Câu Đáp án Mã đề Câu Đáp án 007 1 C 008 1 A 007 2 B 008 2 B 007 3 C 008 3 D 007 4 B 008 4 C 007 5 D 008 5 C 007 6 C 008 6 B 007 7 B 008 7 B 007 8 D 008 8 B 007 9 A 008 9 A 007 10 A 008 10 A 007 11 B 008 11 B 007 12 B 008 12 D 007 13 C 008 13 D 007 14 D 008 14 D 007 15 A 008 15 C 007 16 A 008 16 D 007 17 B 008 17 C 007 18 B 008 18 A 007 19 C 008 19 C 007 20 D 008 20 C 007 21 D 008 21 A Trang 7 Mã đề Câu Đáp án Mã đề Câu Đáp án 009 1 C 010 1 B 009 2 C 010 2 C 009 3 D 010 3 A 009 4 B 010 4 B 009 5 A 010 5 D 009 6 D 010 6 C 009 7 A 010 7 C 009 8 A 010 8 C 009 9 B 010 9 A 009 10 A 010 10 C 009 11 C 010 11 A 009 12 D 010 12 B 009 13 D 010 13 A 009 14 B 010 14 D 009 15 B 010 15 D 009 16 A 010 16 D 009 17 D 010 17 D 009 18 A 010 18 A 009 19 B 010 19 B 009 20 C 010 20 C 009 21 C 010 21 B
II. TỰ LUẬN: ĐỀ LẺ ì2x + a khi x £ 2 ï
Bài 1: Cho hàm số f ( x) = í x - 2
. Tìm tất cả các giá trị của tham số a để hàm số liên khi x > 2 ïî x -1-1 tục tại x = 2 . 2n - 3
Bài 2: Tính giới hạn sau: lim . 3n + 5
Bài 3: Cho tứ diện ABCD có AB = AC = AD = BC = BD = a và CD = a 3 . Gọi I là trung điểm BD .
Tính số đo góc giữa hai đường thẳng AI và BC . ----------- HẾT ---------- Nội dung Điểm ì2x + a khi x £ 2 ï
Bài 1: Cho hàm số f ( x) = í x - 2
. Tìm tất cả các giá trị của tham số a khi x > 2 ïî x -1-1
để hàm số liên tục tại x = 2 .
f (2) = 4 + a 0,25
lim f (x) = 4 + a 0,25 x 2- ® 0,25 x - 2
(x - 2)( x -1 +1) lim f (x) = lim = lim + + + 2 2 x®2 x®2 x®2 x -1 -1 ( x -1) -1 = lim ( x -1 +1) = 2 0,25 x 2+ ® Trang 8
Hàm số liên tục tại x = 2 Û 4 + a = 2 Û a = 2 - 0,25 2n - 3
Bài 2: Tính giới hạn sau: lim . 3n + 5 3 2 2n 3 - - lim = lim n 0,5 3n + 5 5 3+ n 2 0,25 = 3
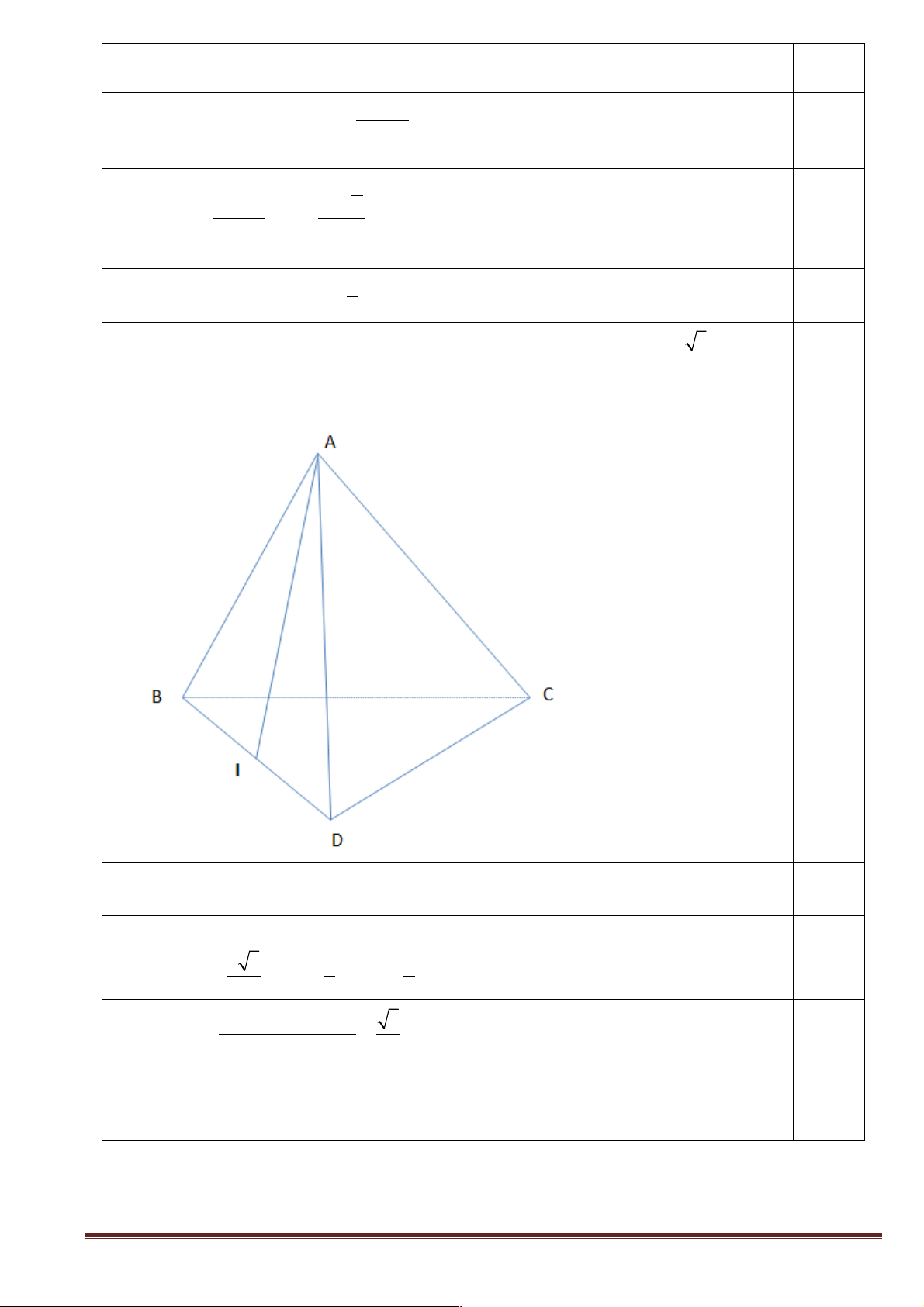
Bài 3: Cho tứ diện ABCD có AB = AC = AD = BC = BD = a và CD = a 3 . Gọi I là
trung điểm BD . Tính số đo góc giữa hai đường thẳng AI và BC . HÌNH VẼ
Gọi M là trung điểm CD. Góc giữa hai đường thẳng AI và BC là góc giữa AI và IM 0,25 Tính 0,25 a 3 a a AI = ; IM = ; AM = 2 2 2 2 2 2 0,25 ∑
AI + IM - AM 3 cos AIM = = 2AI.IM 2
Góc giữa hai đường thẳng AI và BC là góc giữa AI và IM 0,25 bằng 0 30
Học sinh giải cách khác đúng giáo viên căn cứ theo biểu điểm để chấm Trang 9 II. TỰ LUẬN: ĐỀ CHẴN 3 ì x + a khi x £ 3 ï
Bài 1: Cho hàm số f ( x) = í x - 3
. Tìm tất cả các giá trị của tham số a để hàm số liên khi x > 3 ïî x +1-2 tục tại x = 3. 5n - 3
Bài 2: Tính giới hạn sau: lim . 2n + 7
Bài 3: Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a và BC = a 3 . Gọi I là trung điểm AB .
Tính góc giữa hai đường thẳng SI và AC . PHẦN TỰ LUẬN Nội dung Điểm 3 ì x + a khi x £ 3 ï
Bài 1: Cho hàm số f ( x) = í x - 3
. Tìm tất cả các giá trị của tham số a để khi x > 3 ïî x +1-2
hàm số liên tục tại x = 3.
f (3) = 9 + a 0,25
lim f (x) = 9 + a 0,25 x 3- ® 0,25 x - 3
(x - 3)( x +1 + 2) lim f (x) = lim = lim + + + 2 2 x®3 x®3 x®3 x +1 - 2 ( x +1) - 2 = lim( x +1 + 2) = 4 0,25 x 3+ ®
Hàm số liên tục tại x = 3 Û 9 + a = 4 Û a = 5 - 0,25 5n - 3
Bài 2: Tính giới hạn sau: lim . 2n + 7 3 0,5 5 5n 3 - - lim = lim n 2n + 7 7 2 + n 5 0,25 = 2
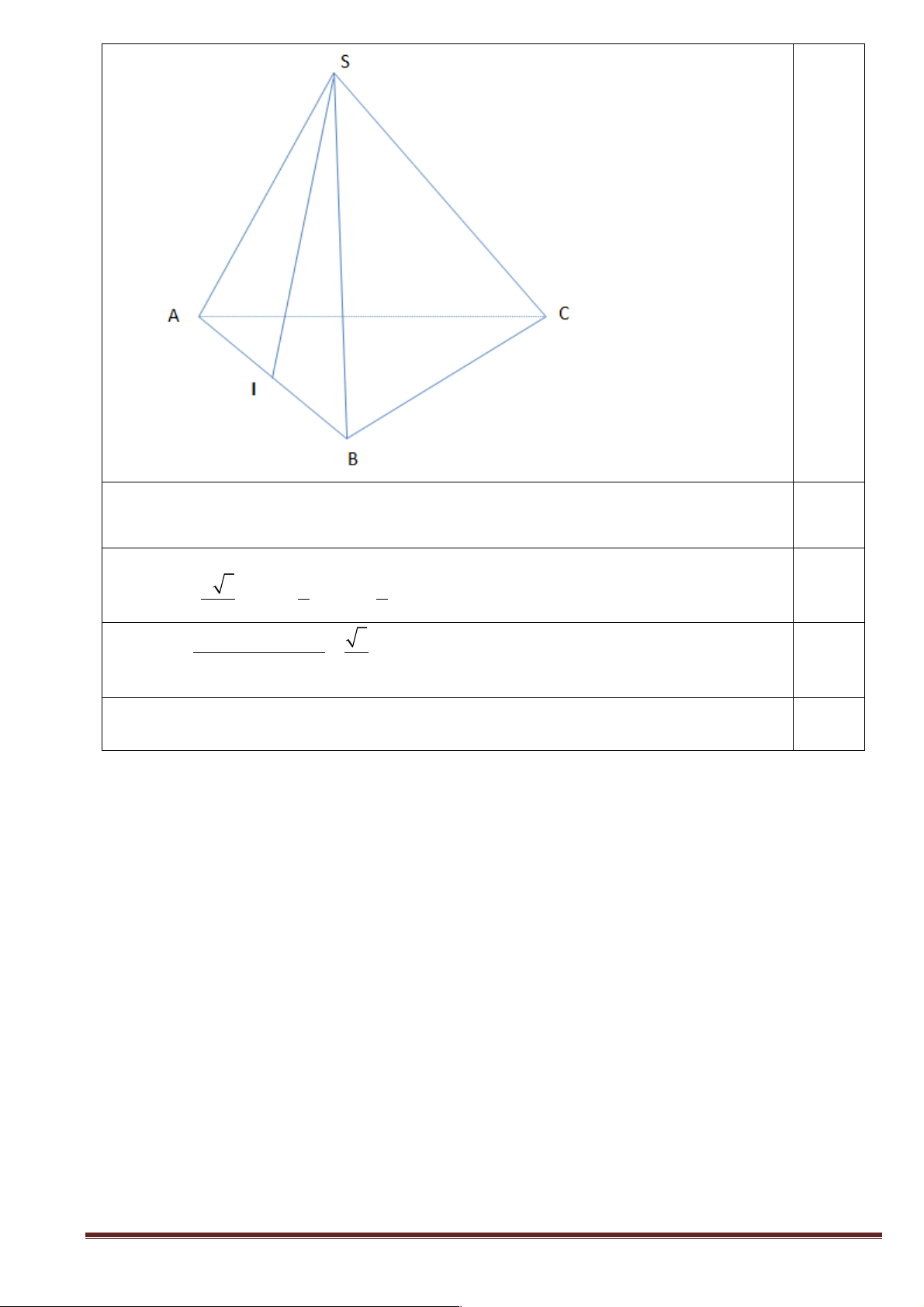
Bài 3: Cho hình chóp S.ABC có SA = SB = SC = AB = AC = a và BC = a 3 . Gọi I là
trung điểm AB . Tính góc giữa hai đường thẳng SI và AC . HÌNH VẼ 0,25 Trang 10
Gọi M là trung điểm BC. Góc giữa SI và AC là góc giữa SI và IM 0,25 Tính 0,25 a 3 a a SI =
; IM = ; SM = 2 2 2 2 2 2 0,25 ∑
SI + IM - SM 3 cos SIM = = 2SI.IM 2
Góc giữa hai đường thẳng SI và AC bằng 0 ˆ SIM = 30 Trang 11