Đề Olympic Toán 11 năm 2020 – 2021 liên cụm trường THPT – Hà Nội

SỞ GD&ĐT HÀ NỘI
ĐỀ THI OLYMPIC NĂM HỌC 2020 – 2021
LIÊN CỤM TRƯỜNG THPT MÔN TOÁN LỚP 11
THANH XUÂN – CẦU GIẤY
Thời gian làm bài: 150 phút MÊ LINH – SÓC SƠN
( Đề thi gồm 01 trang ) ĐÔNG ANH
___________________________________
Bài I ( 4 điểm).   
1) Giải phương trình sin x  3 sin x   1   .  2 
2) Cho tam giác ABC cân tại A . Gọi AH là đường cao xuất phát từ đỉnh A . Biết độ dài các
đoạn thẳng BC, AH , AB theo thứ tự tạo thành một cấp số nhân. Tìm công bội của cấp số nhân đó.
Bài II ( 4 điểm). Trong hộp có 25 tấm thẻ giống nhau được đánh số theo thứ tự từ 1 đến 25 . Rút
ngẫu nhiên ba tấm thẻ từ trong hộp.
1) Có bao nhiêu cách để rút được ít nhất hai tấm thẻ mang số lẻ?
2) Tính xác suất để trong ba số ghi trên ba tấm thẻ rút được không có hai số nào là hai số tự nhiên liên tiếp.
Bài III ( 3 điểm). Tìm số hạng không chứa x trong khai triển nhị thức Niutơn của biểu thức n  1  P  2x  
với x  0 biết rằng n là số nguyên dương thỏa mãn: 2 2 3A  5C  0 . 2  n 1  n  2x  u   2 1 
Bài IV ( 3 điểm). Cho dãy số u : 2
. Xét dãy số v với 2
v  u 1 n   *  . n  n   u  2 n n n u   n 1   3
1) Chứng minh rằng: Dãy số v là một cấp số nhân. n 
2) Tìm công thức số hạng tổng quát của dãy số u . n 
3) Chứng minh rằng: u  u  ...  u  n 1 với mọi số nguyên dương n . 1 2 n
Bài V ( 6 điểm). Cho hình hộp ABC . D AB C  D
  . Gọi G là trọng tâm của tam giác AB C   và I
là trung điểm của đoạn thẳng C D
  . Trên các đoạn thẳng AC và DC lần lượt lấy các điểm E, F 2 1 sao cho AE  AC, DF  DC . 3 3
1) Chứng minh rằng:  AC G
  //  ADI  và EF // BD .
2) Gọi   là mặt phẳng thay đổi và luôn đi qua trung điểm Q của đoạn thẳng AG . Mặt phẳng
  cắt các tia AA , AB , AC lần lượt tại các điểm M , N, P ( không trùng với điểm A ).
AA AB AC
Tìm giá trị lớn nhất của biểu thức T  . . . AM AN AP ------- Hết -------
Họ và tên thí sinh:..................................................................... Số báo danh:.................................... 1/1
HƯỚNG DẪN CHẤM BÀI THI OLYMPIC LIÊN CỤM TRƯỜNG THPT
NĂM HỌC 2020 - 2021 - MÔN TOÁN LỚP 11 *** Bài I. ( 4.0 điểm) Câu Nội dung Điểm    sin x  3 sin x 
1  sin x  3 cos x 1   1.0  2  1 3 1   1    1  sin x  cos x   sin .
x cos  sin .cos x   sin x   1   1.0 2 2 2 3 3 2  3  2 (3.0 điểm)      x    k2 x    k2  3 6  6     . 5   1.0 x    k2 x   k2  3 6  2 Giả sử: AH
AB  a . Khi đó ta có: sin B 
 AH  AB.sin B  a sin B . AB 0.25 BH cos B   BH  A .
B cos B  a cos B  BC  2BH  2 . a cos B ( A  BC cân) AB 2
BC, AH , AB là cấp số nhân 2 2 2 2
 BC.AB  AH  2a .cos B  a .sin B 0.25 (1.0 điểm) cos B  1   2 L 2  
 cos B  2cos B 1  0   0.25 cos B  1   2 AB 1 1 1 1 Khi đó, công bội q      2  2 2 . 0.25 2 AH sin B 1 cos B 2 2   2 2 Bài II. ( 4.0 điểm) Câu Nội dung Điểm
Từ 1 đến 25 có 13 số lẻ, 12 số chẵn. 0.75 1
TH1: Bốc 2 tấm thẻ mang số lẻ, 1 tấm mang số chẵn  Có 2 1 C .C  936 cách 13 12 0.75
(3.0 điểm) TH2: Bốc 3 thẻ mang số lẻ từ 13 thẻ  Có 3 C  286 cách 13 0.75
Vậy có 936  286  1222 cách bốc được ít nhất 2 thẻ mang số lẻ. 0.75
Bốc 3 thẻ ngẫu nhiên từ 25 thẻ  n 3  C  2300 . 0.25 25
A:"Bốc được 3 thẻ ghi 3 số trong đó không có 2 số nào là hai số tự nhiên liên tiếp "
Gọi 3 số tự nhiên bốc được là a; ;
b c với 1  a  b  c  25 . Do không có 2 số nào là 0.25 2
hai số tự nhiên liên tiếp nên 1  a  b 1 c  2  23 .
(1.0 điểm) Mỗi cách chọn bộ 3 số a; ;bc thỏa mãn đề bài tương ứng với một cách chọn bộ 3 số 0.25
tự nhiên phân biệt a;b 1;c  2 từ tập 1;2;...;22;2  3  n A 3  C 1771. 23 n A 77
Xác suất để xảy ra biến cố A là: P  A     . 0.25 n  100 1/4 Bài III. ( 3.0 điểm) Nội dung Điểm ĐK: n  *  ,n  3. n 1 ! n! 0.5 2 2   3A  5C  0  3.  5.  0 n 1  n (n 1 2)! 2!.n  2! n n  n   3.n   1 n  2  1 12 T/m 2    5.
 0  n 13n 12  0   . 1.0 2 n  1  L (3.0 điểm) 12 12  1  k k  1 k  2x    1  C . 2x .  1 k k k  C .2  k.  k x  1.0 2      12 12  2    12 2 12 3 12 12  2x  k0  2x  k0
Số hạng không chứa x  12  3k  0  k  4 0.5
 Số hạng cần tìm:  4 4 4 1 .C .2  7920 . 12 Bài IV. ( 3.0 điểm) Câu Nội dung Điểm Dễ thấy: u  0 n  *. n 0.75 1 2 2 2 u  2 u  2 u  2 1 n 2 n 2 n 2 u   u   u 1  1  u 1  u  n n n n  2 1 1 1 1 1 n  (1.5 điểm) 3 3 3 3 1  1 v
 v n   *  dãy v là cấp số nhân với công bội q  . n  0.75 n 1  3 n 3 1 n 1 1   
Dãy v là cấp số nhân với q  và 2 v  u 1  1 nên v  . 0.5 n  1 1 n   2 3  3  (1.0 điểm) n 1  n 1  1   1  2   u 1   u  1 . 0.5 n      3 n   3 
Áp dụng bđt Bunhiacopxki ta có: u  u  ... u     u  u   u n 2 1 1 ... 1 2 2 2 ... 1 2 1 2 n   u  u ... u  n u  u   u . n 2  2 2 2 ... 1 2 1 2 n  0.25 0 1 n 1  3  1   1   1  3  1  Mà 2 2 2 u  u  ...  u  1 1 ... 1  n  . 1         . (0.5 điểm) 1 2 n  3   3   3  2  3n   3  1 
Do đó u  u  ... u  n n    n n   n  n   n  n 2 1   n   2 2 1  2 2 1 1 2  2  3  0.25
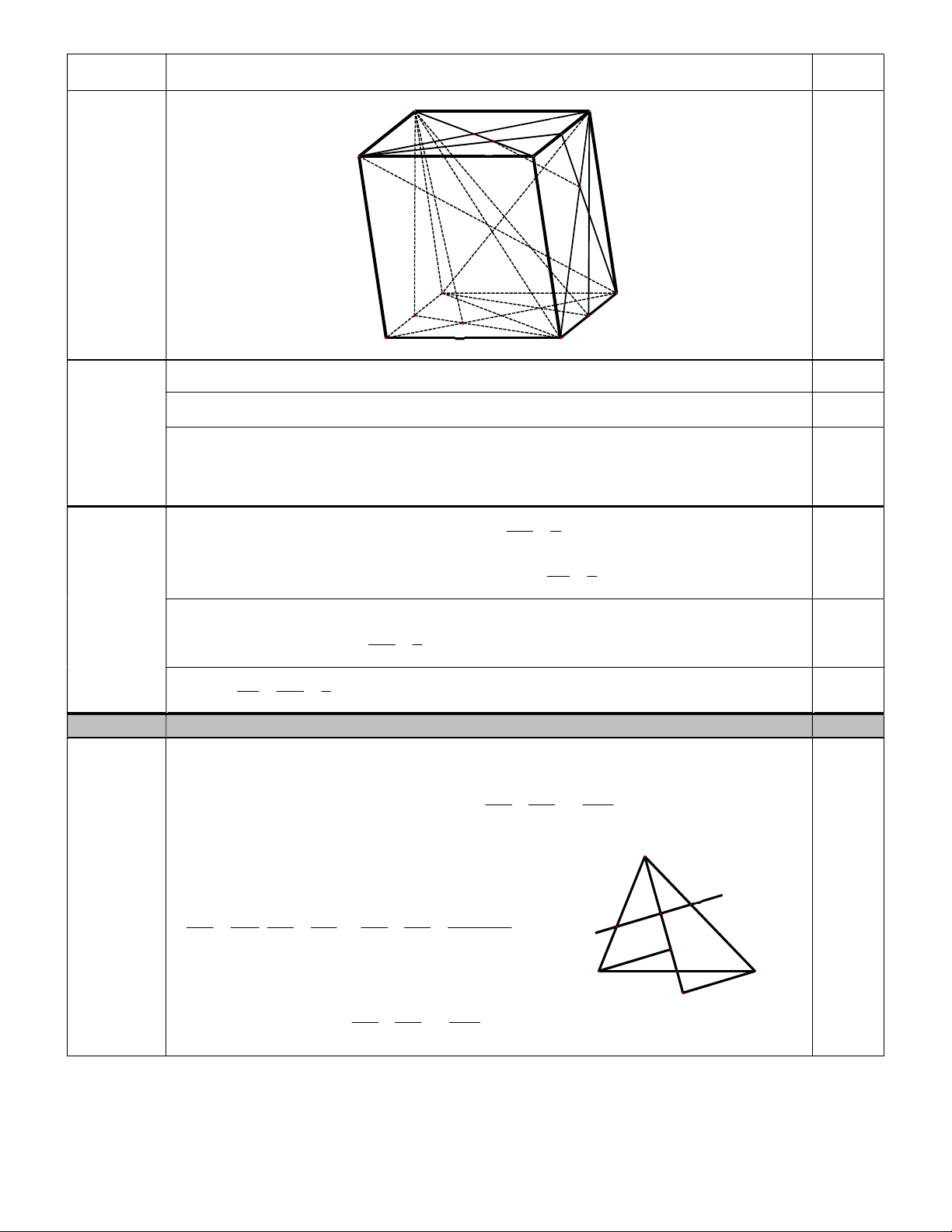
 u  u ... u  n 1. 1 2 n 2/4 Bài V. ( 6.0 điểm) Câu Nội dung Điểm A D O J E B C F Hình vẽ A' D' K I G B' C' C G   A B
   K  K là trung điểm của AB  AIC K
 là hình bình hành  A I //C K  1.0 1
ADIK là hình bình hành  AD//IK, AD  IK   DI //AK 0.5 (Ý 1) AI // C K  , DI // AK  (2.5 điểm)   AC G  :C K
  AK  K    AC G   //  A D  I  . 1.0
 ADI : AI  DI  I  CE 2
AC  BD  O  O là trung điểm của AC 
  E là trọng tâm BCD 0.5 CO 3  JE 1
nếu BE  CD  J thì J là trung điểm CD và  . 0.5 1 JB 3 (Ý 2)
Chứng minh tương tự: F là trọng tâm C  DD 0.5 (2.5 điểm)  JF 1 D , F, J thẳng hàng và  JD 3 0.5 JE JF 1 B  DD :    EF / /BD . 0.5 JB JD 3 (Cách 1) Chứng minh: 
ABC , trung tuyến AM . Giả sử đường thẳng d cắt các tia AB AC AM
AB, AC, AM lần lượt ở D, E, F . Khi đó:   2 (*). AD AE AF
. Vẽ BH ,CI song song với d với H, I  AM . A 2
. Theo định lý Ta let ta có: E (1.0 điểm) AB AH AC AI AB AC AH  AI F  ,     D AD AF AE AF AD AE AF H . Mà B  HM  C
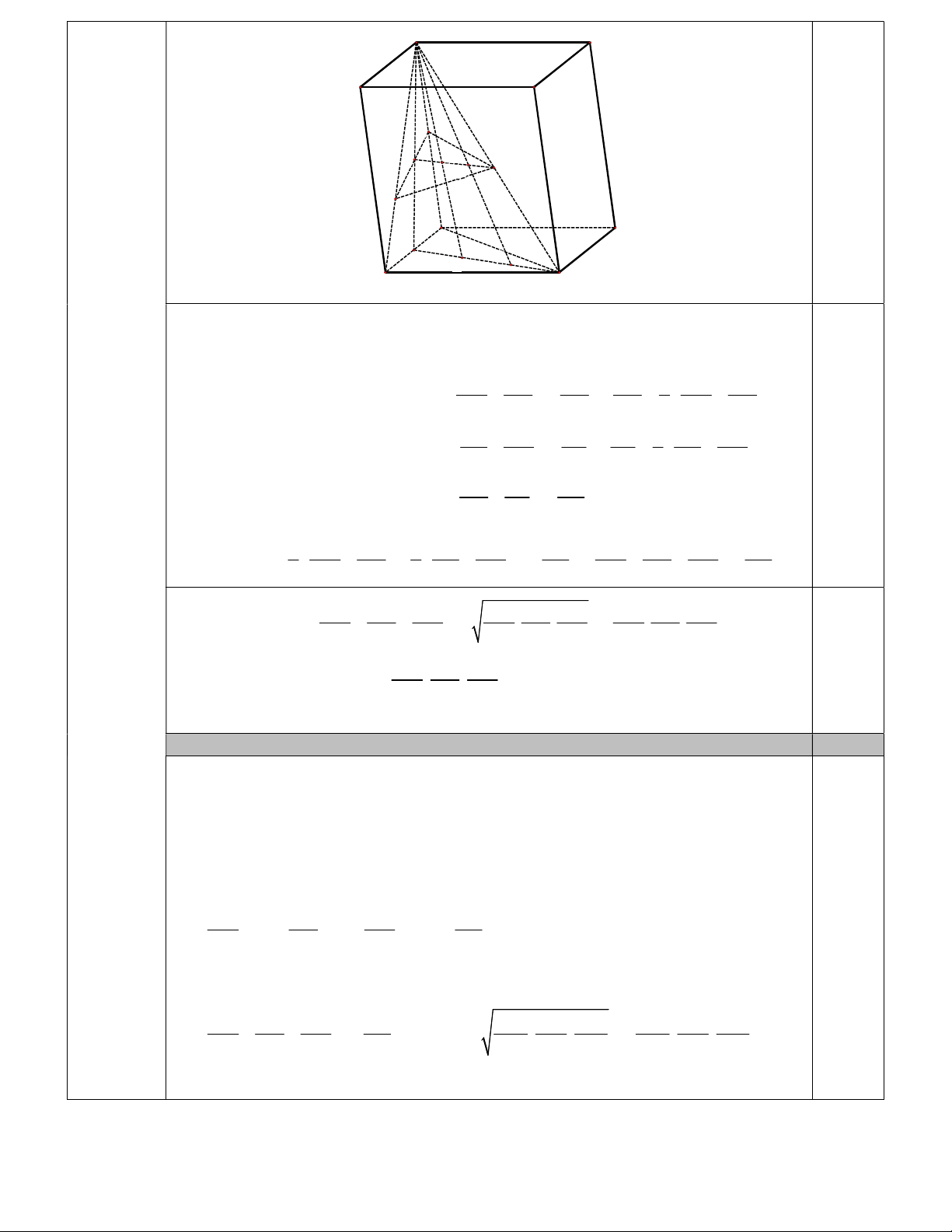
 IM g.c.g  MH  MI B M C AB AC AM I  AH  AI  2AM    2 . 0.25 AD AE AF 3/4 A D B C M Q H P R N A' D' K L G B' C' MN  AK  H  ; P ; Q H thẳng hàng.
Gọi L là trung điểm của C G  và AL  PH  R .      Áp dụng (*): AA AB AK AK AA AB  A
 AB , trung tuyến AK : 1   2      (1) AM AN AH AH 2  AM AN  AG AC AL AL 1  AG AC  Áp dụng (*): A
 GC , trung tuyến AL :   2      (2) 0.5 AQ AP AR AR 2  AQ AP  Áp dụng (*): AK AL AG A  KL, trung tuyến AG :   2 (3) AH AR AQ 1  AA AB  1  AG AC  AG AA AB AC AG Từ (1),(2),(3):     2     3  6     2  AM AN  2  AQ AP  AQ AM AN AP AQ          Áp dụng bđt Côsi: AA AB AC AA AB AC AA AB AC 3    3. . .  . .  8 . AM AN AP AM AN AP AM AN AP AA AB AC 0.25
Vậy giá trị lớn nhất của T  . .
bằng 8 khi M , N, P lần lượt là trung AM AN AP
điểm của AA , AB , AC    //  A B  C   . (Cách 2) . Chứng minh: Nếu ,
A B,C,G đồng phẳng thì với mọi điểm O bất kỳ, ta có     OG  .
x OA  y.OB  z.OC với x  y  z  1. 0.25
   
. Ta có: G là trọng tâm của A  B C
  nên AA  AB  AC  3AG . AA  AB  AC  AG   .AM  .AN  .AP  3. .AQ . 0.25 AM AN AP AQ    
. Vì M , N, P,Q đồng phẳng nên AQ  .
x AM  y AN  z AP với x  y  z  1 AA AB AC AG AA AB AC AA AB AC 3     3.  6  6  3 . .  . .  8 . 0.25 AM AN AP AQ AM AN AP AM AN AP
. Vậy GTLN của T bằng 8 khi   //  A B  C   . 0.25
Ghi chú: Thí sinh có lời giải theo phương pháp khác, nếu đúng vẫn cho điểm tối đa (GK tự chia điểm thành phần). 4/4
Document Outline

• 1. De Olympic cụm - Mon Toan - Lớp 11 nam 2021
• 1. Dap an Olympic cụm - Mon Toan - Lớp 11 nam 2021