Đề ôn tập Toán 11 HK2 năm 2022 (có đáp án)

Đề ôn tập Toán 11 HK2 năm 2022 có đáp án (Đề 1) được soạn dưới dạng file PDF gồm 5 trang giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Các bạn xem và tải về ở dưới.

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu chung Toán 11

Môn: Toán 11

Thông tin:

5 trang 9 tháng trước

Tác giả:

Profile Thùy Dương (H)
Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
(Đề có 02 trang)
ĐỀ KIỂM TRA CUỐI HỌC KỲ II
Môn: Toán - Lớp 11
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
I. TRẮC NGHIỆM (3,0 điểm)
Chọn phương án trả lời đúng cho các câu hỏi sau:
Câu 1. Nếu thì bằng bao nhiêu?
A. . B. . C. . D. .
Câu 2. Tính đạo hàm của hàm số sau .
A. . B. . C. . D. .
Câu 3. Cho hàm số . Khẳng định nào dưới đây đúng?
A. . B. .
C. . D. .
Câu 4. Tìm để hàm số liên tục tại điểm .
A. . B. . C. . D. .
Câu 5. Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ
bằng 1 là
A. . B. 5. C. 4. D. .
Câu 6. Một chất điểm chuyển động thẳng xác định bởi công thức , tính bằng
giây, tính bằng . Tính gia tốc của chất điểm khi vận tốc đạt .
A. . B. . C. . D. 11.
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết rằng
Khẳng định nào sau đây đúng?
A. . B. . C. . D.
Câu 8. Hàm số có đạo hàm là
A. B. C. D.
Câu 9. Cho hình chóp có các cạnh bên và cạnh đáy đều bằng . Gọi là trung
điểm . Mặt phẳng vuông góc với mặt phẳng nào dưới đây?
A. . B. . C. . D. .
( )
0
lim 5
®
=
x
fx
( )
0
lim 3 4
®
-
éù
ëû
x
xfx
17-
1-
1
20-
2
2
'
(2)
=
-
y
x
2
11
'
(2)
-
=
-
y
x
2
5
'
(2)
-
=
-
y
x
2
10
'
(2)
=
-
y
x
2
() 2 4 5fx x x=-+
lim ( )
x
fx
®-¥
=-¥
lim ( )
x
fx
®-¥
=+¥
lim ( ) 2
x
fx
®-¥
=
lim ( ) 2
x
fx
®-¥
=-
m
( )
2
1
1
1
21
ì
-
¹
ï
=
-
í
ï
+=
î
x
khi x
fx
x
m khi x
0
1x =
3=m
0=m
4=m
1=m
32
41yx x=- +
5-
4-
( )
2
83vt t t=+
t
( )
vt
( )
/ms
11
( )
/ms
20
14
2
,.SA SC SB SD==
CD AD^
()CD SBD^
()AB SAC^
()SO A BCD^
2
cos 3yx=
'6sin6.yx=
'2cos3.yx=
' 3sin 6 .yx=-
' 3sin 3 .yx=-
.S ABCD
a
M
SA
( )
MBD
( )
SBC
( )
SAC
( )
SBD
( )
ABCD
Trang 2
Câu 10. Cho hàm số , là tham số. Biết rằng tồn
tại giá trị sao cho , . Khi đó thuộc khoảng nào sau đây?
A. . B. . C. . D. .
Câu 11. Cho hình chóp có đáy là hình vuông cạnh ,
Khoảng cách từ điểm đến mặt phẳng bằng
A. . B.
. C.
. D.
.
Câu 12. Cho ( là phân số tối giản; là số nguyên). Tính
tổng .
A. . B. . C. . D. .
II. TỰ LUẬN (7,0 điểm)
Câu 13. (3,0 điểm)
1) Tính các giới hạn sau:
a) . b)
.
2) Tính đạo hàm của các hàm số sau:
a) với . b) .
Câu 14. (1,0 điểm) Cho hàm số
có đồ thị là . Viết phương trình tiếp tuyến
của tại điểm có tung độ bằng .
Câu 15. (2,5 điểm) Cho hình chóp có đáy là hình vuông tâm , cạnh .
Mặt bên là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
lần lượt là trung điểm của .
a) Chứng minh rằng và .
b) Gọi là góc giữa đường thẳng và mặt phẳng . Tính .
c) Tính khoảng cách từ đến .
Câu 16. (0,5 điểm) Cho hàm số có đồ thị là . Biết cắt
trục hoành tại 3 điểm phân biệt có hoành độ . Tính giá trị biểu thức
.
===== HẾT =====
( ) ( ) ( )
32
1
2232022
3
=-- --+fx x m x m x
m
0
m
( )
0fx
¢
³
x"Î!
0
m
( )
0;2
( )
3; 1--
( )
3; 6
( )
4; 2--
.S ABCD
ABCD
2a
()SA ABCD^
D
()SAC
2a
a
22
3
a
2
2
a
2
3
2
1
235
lim
32
x
xx x a
xx b
®
æö
++- +
=
ç÷
ç÷
-+
èø
a
b
,ab
22
Pa b=+
5P =
3P =
2P =
2P =-
2
3
712
lim
3
x
xx
x
®
-+
-
(
)
22
lim 1
x
xx x
®+¥
+- +
4
2yx x=+
0x >
2 cos 3yxx=+
3
31yx x=-+
( )
C
( )
C
3
.S ABCD
ABCD
O
a
( )
SAB
,HK
,AB BC
( )
SH ABCD^
( ) ( )
SAD SAB^
j
SC
( )
ABCD
tan
j
K
( )
SAD
( )
32
() 0fx ax bx cx da=+++ ¹
( )
C
( )
C
123
,,xxx
( ) ( ) ( )
123
111
'''
D
fx fx fx
=++
Trang 3
I. TRẮC NGHIỆM (3,0 điểm)
Câu
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
Đáp
án
D
A
B
B
A
B
D
C
B
A
A
A
II. TỰ LUẬN (7,0 điểm)
Câu
Ý
Nội dung
Điểm
13
1
1) Tính các giới hạn sau:
1,5
điểm
a)
0,75
b)
0,75
2
2) Tính đạo hàm của các hàm số sau:
1,5
điểm
a)
0,75
b) .
0,75
14
Cho hàm số
có đồ thị là . Viết phương trình tiếp tuyến
của tại điểm có tung độ bằng
1,0
điểm
Ta có: .
0,25
Gọi là tiếp điểm
Với
0,25
. Phương trình tiếp tuyến:
. Phương trình tiếp tuyến: .
0,5
15
Cho hình chóp có đáy là hình vuông tâm , cạnh .
Mặt bên là tam giác đều và nằm trong mặt phẳng vuông góc với
đáy. Gọi lần lượt là trung điểm của .
2,5
điểm
( )( )
( )
2
33 3
34
712
lim lim lim 4 1
33
xx x
xx
xx
x
xx
®® ®
--
-+
==-=-
--
(
)
22
22
2
1
1
11
lim 1 lim lim
2
11
1
11
xxx
x
x
xx x
xx x
xx
®+¥ ®+¥ ®+¥
-
-
+- + = = =
++ +
++ +
43
1
2'4yx x y x
x
=+ Þ= +
2 cos 3 ' 2 sin 3yxxy x=+Þ=-+
3
31yx x=-+
( )
C
( )
C
3
2
33yx
¢
=-
( )
00
;Mx y
3
000 00
3320 2,1yxx xx=Û - -=Û = =-
•
0
1(1)0xy
¢
=- Þ - =
3y =
•
0
2(2)9xy
¢
=Þ =
9( 2) 3 9 15yx x=-+=-
.S ABCD
ABCD
O
a
( )
SAB
,HK
,AB BC
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM
ĐỀ KIỂM TRA CUỐI HỌC KỲ II
Môn: Toán - Lớp 11
(Hướng dẫn chấm có 03 trang)
Trang 4
a) Chứng minh rằng và .
b) Gọi là góc giữa đường thẳng và mặt phẳng . Tính
.
c) Tính khoảng cách từ đến .
a)
Theo Vì là tam giác đều và là trung điểm của
Vì theo giao tuyến nên .
0,5
Ta có .
Mà , suy ra
0,5
b)
Có nên HC là hình chiếu của SC trên .
Do đó .
Xét D là tam giác đều cạnh a và SH là đường cao nên .
Tứ giác là hình vuông cạnh nên
Vậy .
0,5
0,25
0,25
c)
Vì
Trong mp kẻ
Có
Do đó .
0,25
Xét tam giác SHA có HE là đường cao nên
0,25
( )
SH ABCD^
( ) ( )
SAD SAB^
j
SC
( )
ABCD
tan
j
K
( )
SAD
SABD
H
AB SH ABÞ^
( ) ( )
SAB ABCD^
AB
( )
SH ABCD^
( )
SH ABCD SH AD^Þ^
AB AD^
( ) ( ) ( )
AD SAB SAD SAB^Þ ^
( )
SH ABCD^
( )
ABCD
( )
( )
∑
( )
∑
∑
,,SC ABCD SC HC SCH
j
===
SAB
3
2
a
SH =
ABCD
a
22
5
2
a
HC BC BH=+=
15
tan
5
SH
HC
j
==
( ) ( )
( )
( )
( )
( )
( )
// // , , 2 ,BC AD BC SAD d K SAD d B SAD d H SADÞÞ ==
( )
SAB
( )
HE SA E SA^Î
( ) ( )
SAD SAB^
( )
HE SADÞ^
( )
( )
( )
( )
,,2dH SAD HE dK SAD HE=Þ =
22
.3
4
SH HA a
HE
SH HA
==
+
Trang 5
Vậy .
16
Cho hàm số có đồ thị là . Biết cắt
trục hoành tại 3 điểm phân biệt có hoành độ . Tính giá trị biểu
thức .
0,5
Điểm
Vì cắt trục hoành tại 3 điểm phân biệt có hoành độ .
.
Suy ra .
Do đó
Vậy
0,25
0,25
( )
( )
3
,2
2
a
dK SAD HE==
( )
32
() 0fx ax bx cx da=+++ ¹
( )
C
( )
C
123
,,xxx
( ) ( ) ( )
123
111
'''
D
fx fx fx
=++
( )
C
123
,,xxx
( )( )( )
123
()fx ax x x x x xÞ=- - -
( ) ( )( ) ( )( ) ( )( )
23 13 12
'fx axx xx axx xx axx xx=- -+- -+- -
( ) ( )( )
( ) ( )( )
( ) ( )( )
11213
22123
33132
'
'
'
fx ax x x x
fx ax x x x
fx ax x x x
=- -
=- -
=- -
( ) ( ) ( )
( )( ) ( )( ) ( )( )
123
1213 2123 3132
111
'''
111
0
D
fx fx fx
ax x x x ax x x x ax x x x
=++
=++=
-- -- --
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA CUỐI HỌC KỲ II Môn: Toán - Lớp 11 (Đề có 02 trang)
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
I. TRẮC NGHIỆM (3,0 điểm)
Chọn phương án trả lời đúng cho các câu hỏi sau:
Câu 1. Nếu lim f (x) = 5 thì lim é3x - 4 ë
f ( x)ù bằng bao nhiêu? û x®0 x®0 A. 17 - . B. 1 - . C. 1. D. 20 - . 3 - x + 4
Câu 2. Tính đạo hàm của hàm số sau y = . x - 2 - - A. 2 11 5 10 y ' = . B. y ' = . C. y ' = . D. y ' = . 2 (x - 2) 2 (x - 2) 2 (x - 2) 2 (x - 2) Câu 3. Cho hàm số 2
f (x) = 2x - 4x + 5 . Khẳng định nào dưới đây đúng?
A. lim f (x) = -¥.
B. lim f (x) = +¥. x®-¥ x®-¥
C. lim f (x) = 2. D. lim f ( ) x = 2 - . x®-¥ x®-¥ 2 ì x -1 ï khi x ¹ 1
Câu 4. Tìm m để hàm số f (x) = í x -1
liên tục tại điểm x = . 1 0 ïîm+ 2 khi x = 1 A. m = 3 . B. m = 0 . C. m = 4 . D. m = 1.
Câu 5. Hệ số góc của tiếp tuyến với đồ thị hàm số 3 2
y = x - 4x +
1 tại điểm có hoành độ bằng 1 là A. 5 - . B. 5. C. 4. D. 4 - .
Câu 6. Một chất điểm chuyển động thẳng xác định bởi công thức v(t) 2
= 8t + 3t , t tính bằng
giây, v(t) tính bằng(m / s). Tính gia tốc của chất điểm khi vận tốc đạt 11 (m / s). A. 20 . B.14. C. 2 . D. 11.
Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết rằng
SA = SC, SB = .
SD Khẳng định nào sau đây đúng?
A. CD ^ AD .
B. CD ^ (SBD).
C. AB ^ (SAC).
D. SO ^ (ABCD) Câu 8. Hàm số 2
y = cos 3x có đạo hàm là
A. y ' = 6sin 6 . x
B. y ' = 2cos3x . C. y ' = 3 - sin 6 .x D. y ' = 3 - sin3 .x
Câu 9. Cho hình chóp S.ABCD có các cạnh bên và cạnh đáy đều bằng a . Gọi M là trung
điểm SA. Mặt phẳng (MBD) vuông góc với mặt phẳng nào dưới đây? A. (SBC). B. (SAC). C. (SBD).
D. ( ABCD). Trang 1
Câu 10. Cho hàm số f (x) 1 3 = x - (m - 2) 2
x - (2m - 3) x + 2022, m là tham số. Biết rằng tồn 3
tại giá trị m sao cho f ¢(x) ³ 0, x
" Î ! . Khi đó m thuộc khoảng nào sau đây? 0 0 A. (0;2). B. ( 3; - - ) 1 . C. (3;6). D. ( 4; - - 2).
Câu 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a , SA ^ (ABCD)
Khoảng cách từ điểm D đến mặt phẳng (SAC) bằng 2a 2 a 2 A. a 2. B. a . C. . D. . 3 2 2 æ 3 ö a Câu 12. Cho
x + x + 2 - 3x + 5 a lim ç ÷ =
( là phân số tối giản; a, b là số nguyên). Tính 2 x 1 ® ç x - 3x + 2 ÷ b è ø b tổng 2 2
P = a + b .
A. P = 5.
B. P = 3. C. P = 2 . D. P = 2 - .
II. TỰ LUẬN (7,0 điểm)
Câu 13. (3,0 điểm)
1) Tính các giới hạn sau: 2 x - 7x +12 a) lim . b) x 3 ® x - 3 2 2 lim
x + x - x +1 . x®+¥ ( )
2) Tính đạo hàm của các hàm số sau: a) 4
y = x + 2 x với x > 0 .
b) y = 2cos x + 3x.
Câu 14. (1,0 điểm) Cho hàm số 3
y = x - 3x +
1 có đồ thị là (C). Viết phương trình tiếp tuyến
của (C) tại điểm có tung độ bằng 3.
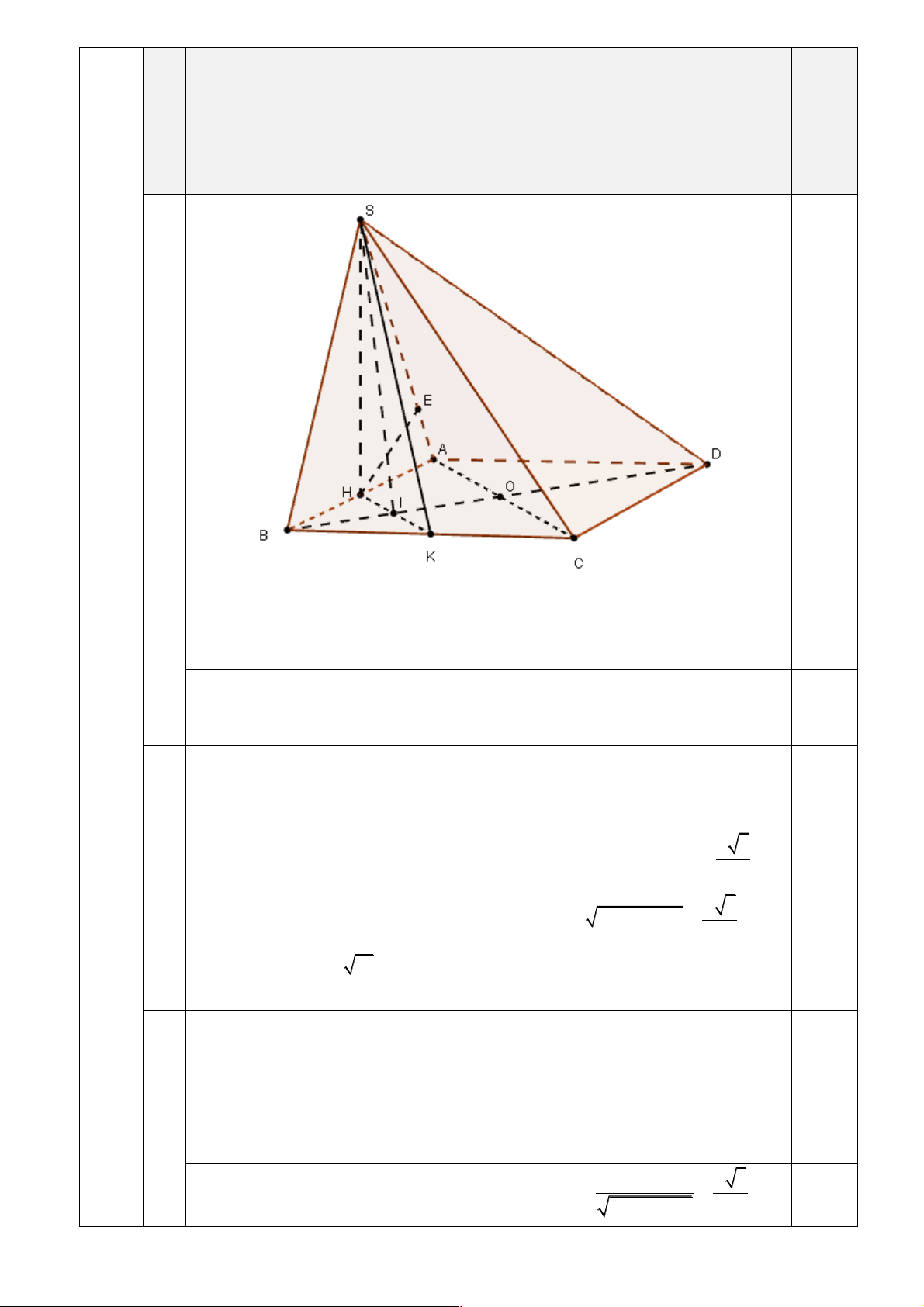
Câu 15. (2,5 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a .
Mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi
H , K lần lượt là trung điểm của AB, BC.
a) Chứng minh rằng SH ^ ( ABCD) và (SAD) ^ (SAB).
b) Gọi j là góc giữa đường thẳng SC và mặt phẳng ( ABCD). Tính tanj.
c) Tính khoảng cách từ K đến (SAD).
Câu 16. (0,5 điểm) Cho hàm số 3 2
f (x) = ax + bx + cx + d (a ¹ 0) có đồ thị là (C). Biết (C) cắt
trục hoành tại 3 điểm phân biệt có hoành độ x , x , x . Tính giá trị biểu thức 1 2 3 1 1 1 D = + + . f '(x f ' x f ' x 1 ) ( 2) ( 3) ===== HẾT ===== Trang 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM
ĐỀ KIỂM TRA CUỐI HỌC KỲ II Môn: Toán - Lớp 11
(Hướng dẫn chấm có 03 trang)
I. TRẮC NGHIỆM (3,0 điểm) Câu 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. Đáp D A B B A B D C B A A A án
II. TỰ LUẬN (7,0 điểm) Câu Ý Nội dung Điểm
1 1) Tính các giới hạn sau: 1,5 điểm 2 x - 7x +12 (x -3)(x -4) a) lim = lim = lim(x - 4) = - 1 0,75 x 3 ® x 3 ® x 3 x - 3 x - 3 ® 1 1- x -1 1 b) 2 2 lim + - +1 = lim = lim x x x x = x®+¥ ( ) 0,75 x®+¥ 2 2
x + x + x +1 x®+¥ 1 1 2 13 1+ + 1+ 2 x x 1,5 2
2) Tính đạo hàm của các hàm số sau: điểm 1 a) 4 3
y = x + 2 x Þ y ' = 4x + 0,75 x
b) y = 2cos x + 3x Þ y ' = 2 - sin x + 3. 0,75 Cho hàm số 3
y = x - 3x +1 có đồ thị là (C). Viết phương trình tiếp tuyến 1,0
của (C) tại điểm có tung độ bằng 3 điểm Ta có: 2
y¢ = 3x - 3. 0,25 14
Gọi M (x ; y 0 0 ) là tiếp điểm 0,25 Với 3
y = 3 Û x - 3x - 2 = 0 Û x = 2, x = - 1 0 0 0 0 0 • x = 1 - Þ y (¢ 1
- ) = 0. Phương trình tiếp tuyến: y = 3 0 0,5
• x = 2 Þ y (¢2) = 9. Phương trình tiếp tuyến: y = 9(x - 2) + 3 = 9x -15. 0
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a . 2,5 15
Mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với điểm
đáy. Gọi H , K lần lượt là trung điểm của AB, BC. Trang 3
a) Chứng minh rằng SH ^ ( ABCD) và (SAD) ^ (SAB).
b) Gọi j là góc giữa đường thẳng SC và mặt phẳng ( ABCD). Tính tanj .
c) Tính khoảng cách từ K đến (SAD). Theo Vì SA
D B là tam giác đều và H là trung điểm của AB Þ SH ^ AB 0,5
Vì (SAB) ^ ( ABCD) theo giao tuyến AB nên SH ^ ( ABCD).
a) Ta có SH ^(ABCD)ÞSH ^ AD. 0,5
Mà AB ^ AD , suy ra AD ^ (SAB) Þ (SAD) ^ (SAB)
Có SH ^ ( ABCD) nên HC là hình chiếu của SC trên ( ABCD). 0,5 Do đó (SC ( ∑ABCD)) = (∑ SC HC ) ∑ , , = SCH = j . a 3
Xét D SAB là tam giác đều cạnh a và SH là đường cao nên SH = . b) 2 Tứ giác a 5
ABCD là hình vuông cạnh a nên 2 2
HC = BC + BH = 0,25 2 SH 15 Vậy tanj = = . 0,25 HC 5
Vì BC / / AD Þ BC / / (SAD) Þ d (K,(SAD)) = d ( ,
B (SAD)) = 2d (H,(SAD))
Trong mp (SAB) kẻ HE ^ SA(E ÎSA) 0,25
Có (SAD) ^ (SAB) Þ HE ^ (SAD) c)
Do đó d (H,(SAD)) = HE Þ d (K,(SAD)) = 2HE.
Xét tam giác SHA có HE là đường cao nên SH.HA a 3 HE = = 0,25 2 2 SH + HA 4 Trang 4
Vậy d (K (SAD)) a 3 , = 2HE = . 2 Cho hàm số 3 2
f (x) = ax + bx + cx + d (a ¹ 0) có đồ thị là (C). Biết (C) cắt
trục hoành tại 3 điểm phân biệt có hoành độ x , x , x . Tính giá trị biểu 0,5 16 1 2 3 Điểm thức 1 1 1 D = + + . f '(x f ' x f ' x 1 ) ( 2) ( 3)
Vì (C) cắt trục hoành tại 3 điểm phân biệt có hoành độ x , x , x . 1 2 3
Þ f (x) = a(x - x x - x x - x 1 ) ( 2 ) ( 3 ) .
Suy ra f '(x) = a(x - x x - x + a x - x x - x + a x - x x - x 2 ) ( 3 ) ( 1 ) ( 3 ) ( 1 ) ( 2 ) .
f '( x = a x - x x - x 1 ) ( 1 2 )( 1 3) 0,25
Do đó f '(x = a x - x x - x 2 ) ( 2 1)( 2 3)
f '( x = a x - x x - x 3 ) ( 3 1)( 3 2 ) Vậy 1 1 1 D = + + f '( x f ' x f ' x 1 ) ( 2 ) ( 3) 1 1 1 0,25 = + + = a ( 0 x - x x - x a x - x x - x a x - x x - x 1 2 ) ( 1 3 ) ( 2 1)( 2 3) ( 3 1)( 3 2 ) Trang 5