Đề ôn thi giữa kì 2 Toán 11 năm học 2021-2022 - Đề 8 (có đáp án)

ĐỀ ÔN THI GIỮA HỌC KÌ II, NĂM HỌC 2021 - 2022 MÔN: TOÁN 11
Thời gian làm bài: 45 phút, không kể thời gian phát đề
A. PHẦN TRẮC NGHIỆM (7,0 điểm): Câu 1: lim n q bằng:
A. +¥ nếu q ³ 1.
B. 0 nếu q < 1.
C. 0 nếu q > . 1
D. 0 nếu q £ 1.
Câu 2: Chọn mệnh đề sai trong các mệnh đề sau: 1
A. lim c = c nếu c là hằng số. B. lim
= 0 với k nguyên dương. k n 1 C. lim = 0. D. lim k
n = 0 với k nguyên dương. n
Câu 3:Trong các mệnh đề dưới đây, mệnh đề nào sai?.
A. Nếu limu = +¥ và limv = a > 0 thì lim(u v = +¥ n n ) . n n æ u ö
B. Nếu limu = a ¹ 0 và limv = ±¥ thì lim n ç ÷ = 0. n n v è n ø æ u ö
C. Nếu limu = a > 0 và limv = 0 thì lim n ç ÷ = +¥. n n v è n ø æ u ö
D. Nếu limu = a < 0 và limv = 0 và v > 0 với mọi n thì lim n ç ÷ = -¥. n n n v è n ø
Câu 4: Cấp số nhân lùi vô hạn là cấp số nhân có công bội q thỏa mãn: A. q < 1. B. q < 1. C. q > 1. D. q > 1.
Câu 5: Trong các khẳng định dưới đây có bao nhiêu khẳng định đúng? (I) lim k
n = +¥ với k nguyên dương. (II) lim n
q = +¥ nếu q < 1. (III) lim n
q = +¥ nếu q > 1 A. 0 . B. 1. C. 3 . D. 2 . Câu 6: Tính 5 2 lim( 2 - n + 3n + 4). A. -¥ . B. +¥ . C. 2 - . D. 5 . 5n + 3 Câu 7: Tính lim . 2n +1 5 A. 1. B. +¥ . C. 2 . D. . 2 3n + 2.5n Câu 8: lim bằng 6.5n - 2.4n 1 1 A. 1 B. C. D. -2 3 2 2 2 2
Câu 9: Tổng vô hạn sau đây S = 2 + + + ...+
+ ... có giá trị bằng 2 3 3 3n 8 A. . B. 3 . C. 4 . D. 2 . 3
Câu 10: Trong các mệnh đề sau, mệnh đề nào sai? Trang 1 1
A. lim c = c(c là hằng số). B. lim = 0. x®-¥ x®+¥ x C. k * lim x = - , ¥ k " Ε . D. lim k x = + , ¥ k + Î! . x®-¥ x®+¥
Câu 11: Trong các mệnh đề sau, mệnh đề nào đúng? A. lim c = 1
x (c là hằng số). B. lim = +¥. 0 x® ®+¥ 0 x x x
C. lim x = x . D. lim k x = 0, k + Î! . 0 x® ®+¥ 0 x x
Câu 12:Chọn khẳng định đúng:
A. lim f (x) = a Û lim f (x) = a.
B. lim f (x) = a Û lim f (x) = a. x + ® - ® 0 x x® x x ® 0 x 0 x 0 x
C. lim f (x) = a Û lim f (x) = lim f (x) = a. D. lim f (x) = a Û lim f (x) = lim f (x). x + - ® + - ® 0 x x® ® x x ® ® 0 x x 0 x 0 x 0 x x 0 x Câu 13: lim( 3 2
-x - 4x +10)bằng x®2 A. +¥ B. 0 C. 10 D. - 14 3 3x - 2 x -1 Câu 14: Tính lim . x®-1 x - 2 5 5 A. 5. B. 1. C. . D. - . 3 3 Câu 15:Tính ( 3 2
lim -x + x + 2). x®+¥ A. 0 . B. -¥ . C. +¥ . D. 2 . 2 x - 2022x + 3 Câu 16:Tính lim . 2
x®+¥ 2x + 2022x 1 1 A. 2022 . B. . C. 2. D. . 2 2022
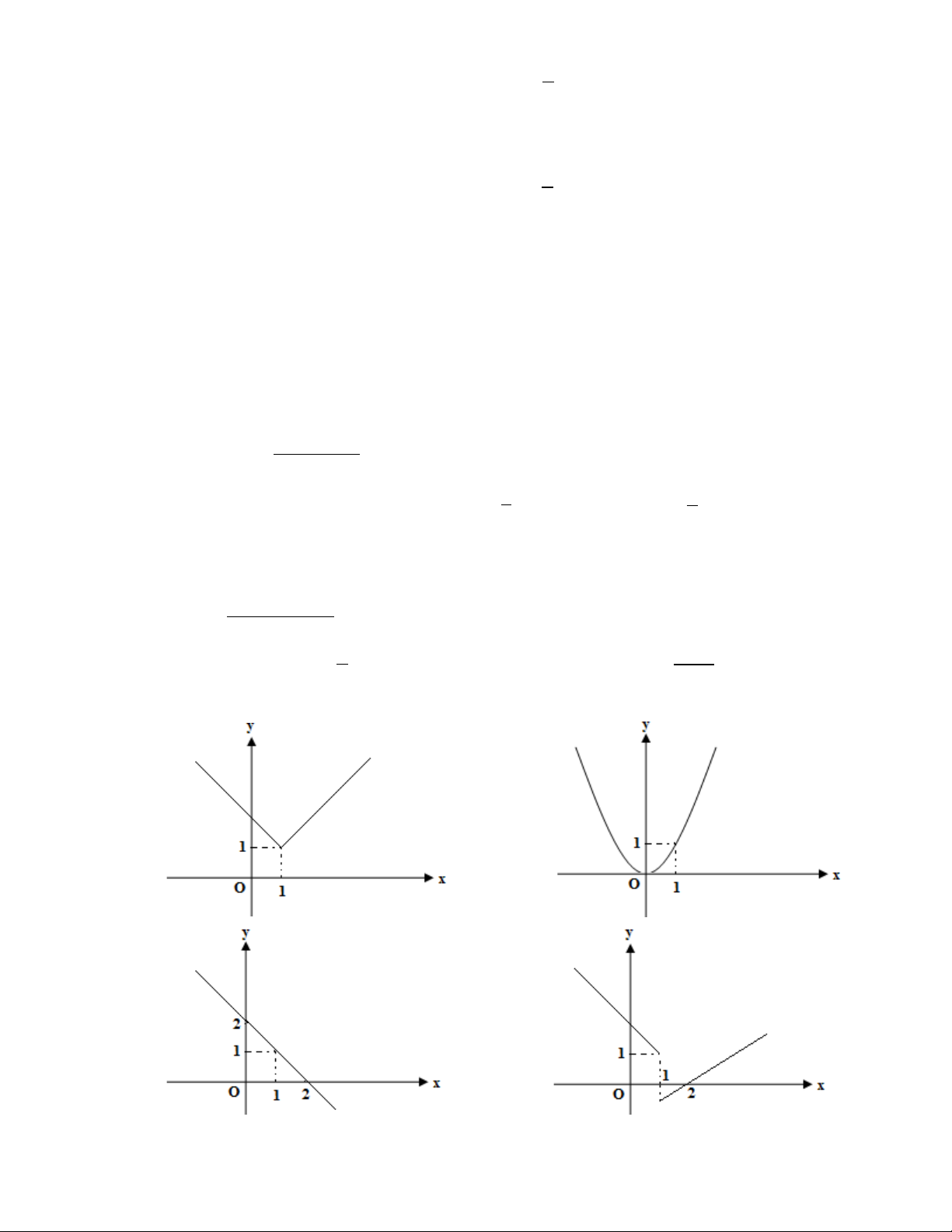
Câu 17: Hình nào trong các hình dưới đây là đồ thị của hàm số không liên tục tại x = 1? A. . B. . C. . D. .
Câu 18: Cho hàm f (x) và g (x) là hai hàm số liên tục tại điểm x . Khẳng định nào sau đây sai? 0 Trang 2
A. Hàm số f (x) - g (x) liên tục tại điểm x .
B. Hàm số f (x).g (x) liên tục tại điểm x . 0 0 f ( x) C. Hàm số
liên tục tại điểm x .
D. Hàm số f (x) + g (x) liên tục tại điểm x . g ( x) 0 0 Câu 19: Cho hàm số 3
f (x) = 3x + 3x - 2. Trong các mệnh đề sau, mệnh đề nào sai?
A. Phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (0; 1).
B. Phương trình f(x) = 0 vô nghiệm trong khoảng (0; 1).
C. Phương trình f(x) = 0 có nhiều nhất là 3 nghiệm.
D. Phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (-1; 1).
Câu 20: Chọn khẳng định sai trong các khẳng định sau: 2 x - 5x + 2 A. Hàm số y =
liên tục trên các khoảng ( ;2 -¥ ), (2;+ ¥). x - 2 2 ì x - 4 ï khi x ¹ 2 -
B. Hàm số f (x) = í x + 2
liên tục tại điểm x = 2 - . ïî 3 - khi x = 2 - C. Hàm số 2
y = x + 8 liên tục tại điểm x = 1.
D. Hàm số y = sin x liên tục trên !
Câu 21: Cho phương trình: 5
x + x -1 = 0 (1). Trong các mệnh đề sau, mệnh đề nào sai?
A. (1) có nghiệm trên khoảng (-1; 1).
B. (1) có nghiệm trên khoảng (0; 1).
C. (1) có nghiệm trên R. D. Vô nghiệm.
Câu 22: Cho lăng trụ ABC.A¢B C
¢ ¢. Gọi M là trung điểm của AC . Khi đó hình chiếu song song của
điểm M lên ( AA B
¢ ¢) theo phương chiếu CB là
A. Trung điểm BC . B.Trung điểm AB . C. Điểm A . D. Điểm B .
Câu 23: Nếu ABC.A¢B C
¢ ¢là hình lăng trụ thì:
A. Các mặt bên là hình vuông.
B. Các mặt bên là hình chữ nhật.
C. Các mặt bên là hình thoi.
D.Các mặt bên là hình bình hành.
Câu 24: Giả sử đường thẳng a song song với phương chiếu l . Hình chiếu song song của đường thẳng a
theo phương l lên mặt phẳng chiếu (P) là:
A. Đường thẳng song song với phương chiếu l .
B. Đường thẳng vuông góc với phương chiếu l .
C. Đường thẳng trên mặt phẳng chiếu (P).
D.Giao điểm của a với mặt phẳng chiếu (P). !
Câu 25: Cho tứ diện ABCD . Hỏi có bao nhiêu vectơ khác vectơ 0 mà mỗi vectơ có điểm đầu, điểm cuối
là hai đỉnh của tứ diện ABCD ? A.12 . B. 4 . C. 10 . D. 8 .
Câu 26: Cho hình lập phương ABC . D A¢B C ¢ D
¢ ¢ . Chọn mệnh đề đúng? !!!" !!!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!" !!!!" "
A. AC = C A
¢ ¢. B. AB + AD+ AC = AA¢.
C. AB = CD.
D. AB +C D ¢ ¢ = 0.
Câu 27: Cho tứ diện ABCD có trọng tâm .
G Mệnh đề nào sau đây sai? !!!" !!!" !!!" !!!"
A. AB,CD là hai đường thẳng chéo nhau.
B. AB + AC + AD = 4AG. !!!" !!!" !!!" !!!" !!!" !!!" !!!" "
C. AB, AC,AD đồng phẳng.
D. AB + BC +CD + DA = 0. !!!" !!!" " !!!" " "
Câu 28: Cho hình lăng trụ ABC.A¢B C
¢ .¢ Đặt AB = a, AA¢ = b, AC = c. Khẳng định nào sau đây đúng? !!!!" " !!!!" " A. " " " " B C
¢ = a +b -c . B. B C ¢ = a - +b -c . !!!!" " !!!!" " C. " " " " B C ¢ = a - -b +c . D. B C ¢ = a - +b +c
B. PHẦN TỰ LUẬN(3,0 điểm): Trang 3 2
ì x - 6x + 5 khi x ¹1 ï 2 ï
Câu 29: Cho hàm số f (x) x -1 = í
. Tìm a để hàm số liên tục tại x = 1. 5 ïa + khi x = 1 ïî 2
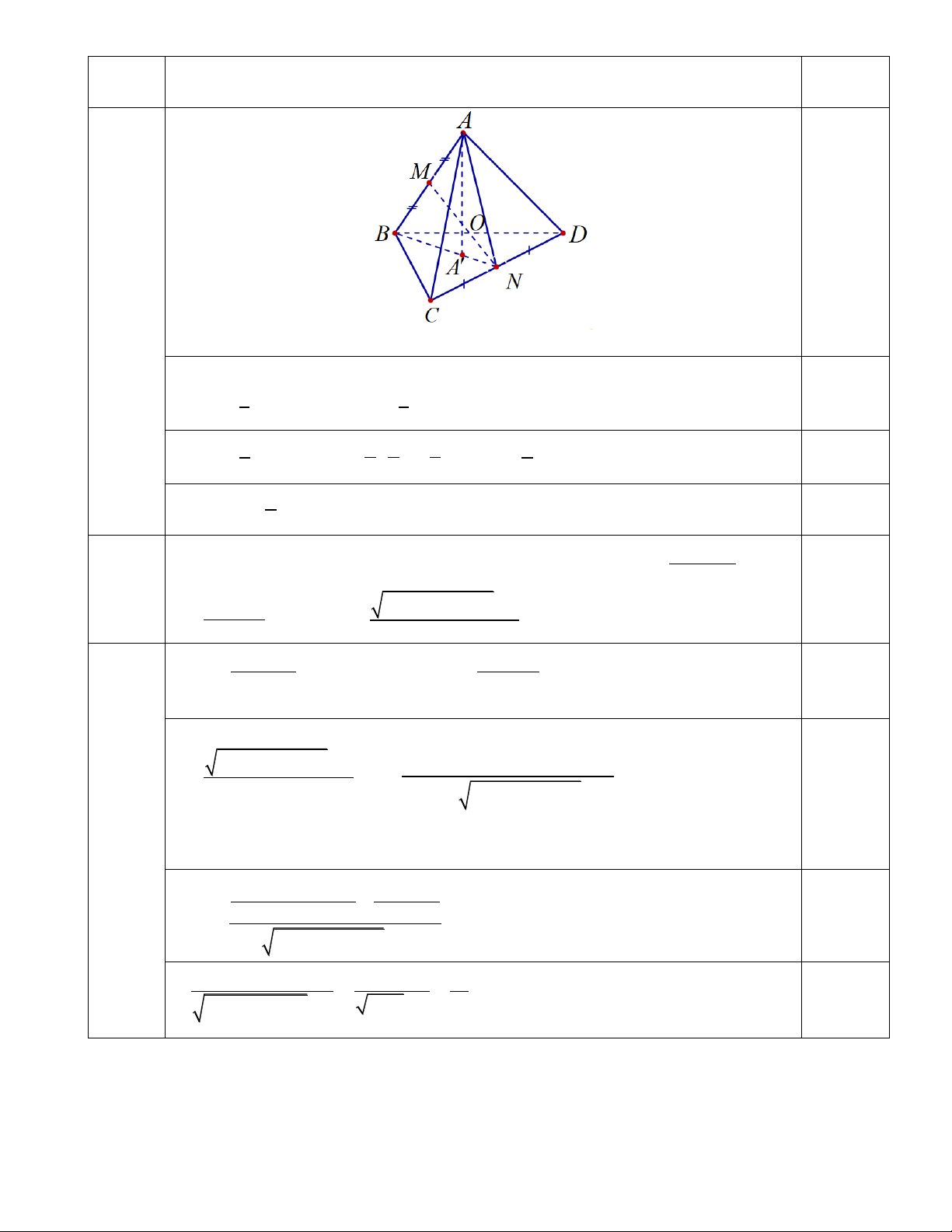
Câu 30: Cho tứ diện ABCD , các điểm M , N lần lượt là trung điểm của AB và CD . Gọi O là trung
điểm của đoạn thẳng MN , điểm A¢ là trọng tâm của tam giác BCD . Chứng minh ba điểm O , A , A¢ thẳng hàng. f (x) - 5 g (x) -1
Câu 31: Cho hàm số f (x) , 𝑔(𝑥) xác định trên ! thỏa mãn lim = 2 và lim = 3 tính x 1 ® x -1 x 1 ® x -1
f ( x).g ( x) + 4 - 3 lim x 1 ® x -1
-------------------------Hết------------------------- ĐÁP ÁN A. PHẦN TRẮC NGHIỆM CÂU 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Đ/AN B D C B D A D B B C C C C C CÂU 15 16 17 18 19 20 21 22 23 24 25 26 27 28 Đ/AN B B D C B B D B D D A D C C B. PHẦN TỰ LUẬN Câu Nội dung trình bày Điểm 2 ì x - 6x + 5 khi x ¹ 1 ï 2 Cho hàm số ï f (x) x -1 = í
. Tìm a để hàm số liên tục tại 29 5 ïa + khi x = 1 ïî 2 x = 1.
Tậpxácđịnh D = ! và 𝑥 = 1 ∈ 𝑅.Ta có: f ( ) 5 1 = a + 2 0,25 2 x - 6x + 5 (x - )1(x -5) x - 5 lim = lim = lim = 2 - 2 x 1 ® x 1 x -1 ® ( x - ) 1 ( x + ) 1 x 1 ® x +1 0,25 Hàm số liên tục tại
x = 1 Û lim f (x) = 5 f ( ) 1 Û a + = 2 - x 1 ® 2 0,25 9 Û a = - . 2
Vậy hàm số liên tục tại x = 1khi 𝑎 = !" 0,25 #
Cho tứ diện ABCD , các điểm M , N lần lượt là trung điểm của AB và Trang 4 30
CD . Gọi O là trung điểm của đoạn thẳng MN , điểm A¢ là trọng tâm
của tam giác BCD . Chứng minh ba điểm O, A, A¢ thẳng hàng. 0,25 !!!" " !!!" " !!!" "
Chọn hệ cơ sở: AB = a, AC = b, AD = c. Ta có: !!!" !!!" !!!" !!!" ! ! ! * 1 1
AA¢ = ( AB + AC + AD) = (a +b + c). 0,25 3 3 !!!" !!!!" !!!" ! ! ! ! ! ! * 1 1 é1 1 ù 1
AO = ( AM + AN ) = a + ê
(b+c) = (a+b+c). 2 2 2 2 ú ë û 4 0,25 !!!" !!!" Vậy 4
AA¢ = AO nên ba điểm O , A , A¢ thẳng hàng. 3 0,25 31 f (x) - 5
Cho hàm số f (x) , 𝑔(𝑥) xác định trên ! thỏa mãn lim = 2 và x 1 ® x -1 g (x) -1
f ( x).g ( x) + 4 - 3 lim = 3 tính lim x 1 ® x -1 x 1 ® x -1 f (x) -5 g (x) -1 Vì lim = 2 Þ f ( ) 1 = 5 và lim = 3 Þ g ( ) 1 = 1 x 1 ® x -1 x 1 ® x -1 0,25
f ( x).g ( x) + 4 - 3
f (x).g (x) -5 lim = lim x 1 ® x 1 ® x -1
(x - )1( f (x).g(x)+4 +3) 0,25
f ( x).ég ë ( x) -1ù f û (x)-5 + 0,25 . x -1 x -1 = lim x 1 ®
( f (x).g(x)+4+3) f ( ) 1 .3 + 2 5.3 + 2 17 = = = 5 + 4 + 3 6 f ( ) 1 .g ( ) 1 + 4 + 3 0,25 Trang 5