Đề tham khảo giữa kì 2 Toán 11 năm 2022 – 2023 THPT Thuận Thành 1 – Bắc Ninh

TRƯỜNG THPT THUẬN THÀNH SỐ 1
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II TỔ TOÁN NĂM HỌC 2022 - 2023 ------------- MÔN: Toán lớp 11
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giáo viên soạn đề: Cô Nguyễn Thị Thắm
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Câu 1. Cho hình chóp S.ABCD có đáy là hình vuông, SA vuông góc với mặt phẳng đáy. Mệnh đề nào dưới đây đúng? A. BA  SAC . B. BA  SBC . C. BA  SAD. D. BA  SCD.
Câu 2. Cho hình lập phương ABCD.AB C  D
  . Số đo góc giữa AB và mặt phẳng ABCDlà A. 30. B. 60 . C. 90 . D. 45.
Câu 3. Cho tứ diệnABCD có tất cả các cạnh bằng a . Gọi M ,N lần lượt là trung điểm của AB và CD
Tính sin số đo góc giữa MN và BCD. 1 3 3 2 A. . B. . C. . D. . 2 3 2 2
Câu 4. Cho hình chóp S.ABCD đáy là hình vuông, cạnh bên SA vuông góc với đáy, SA  AB  a .
Tính diện tích tam giác SBD theo a . 3 3 3 6 A. 2 a . B. 2 a . C. 2 a . D. 2 a 3 4 2 2
Câu 5. Cho tứ diện SABC có SA  SB  SC  AB  AC  a, BC  a 2 . Tính góc giữa hai vectơ   SC và AB . A. 0 60 . B. 0 30 . C. 0 90 . D. 0 120 .
Câu 6. Cho cấp số nhân với công bội là một số dương, biết u  18 và u  162 . Tổng 5 số hạng đầu 3 5
tiên của cấp số nhân đó bằng: A. S  2130 . B. S  672 . C. S  242 . D. S  60 . 5 5 5 5
Câu 7. Cho x , y là các số nguyên thỏa mãn x , 2x 1, 5  4y theo thứ tự đó lập thành 1 cấp số cộng y
và x  2 , x  , 2x  y theo thứ tự đó lập thành 1 cấp số nhân. Tính T  x  y 2 A. T  8 B. T  3 C. T  15 D. T  10. 3n n  2 Câu 8. Tính giới hạn lim được kết quả là 2 n  n  1 A.  . B.  . C. 3 . D. 0 . 1 1 1 1
Câu 9. Tổng S  1     . .   . . bằng 3 9 27 3n 1 3 A. . B. 1. C. 2. D. . 2 2
Câu 10. Cho giới hạn lim f x  2 . Khi đó lim 3f x 5  x 1     x 1     bằng A. 1. B. 2 . C. 2. D. 1.
Câu 11. Trong các mệnh đề sau đây, mệnh đề nào SAI?
A. Nếu đường thẳng d song song với đường thẳng  thì góc giữa chúng bằng 0 .
B. Hai đường thẳng vuông góc với nhau có thể cắt nhau hoặc chéo nhau. 1
C. Cho hai đường thẳng song song. Nếu một đường thẳng vuông góc với đường thẳng này thì cũng vuông
góc với đường thẳng kia.
D. Góc giữa hai đường thẳng chính là góc giữa hai vec-tơ chỉ phương của chúng. ax b  x 2 Câu 12. Biết rằng lim  . Khi đó 2a  3b bằng 2 x1 x  x  2 3 A. 13 . B. 12 . C. 1  3. D. 1  2.
PHẦN II. TỰ LUẬN (7,0 điểm)
Câu 13. (2.5 điểm) Tính các giới hạn sau 2 a)  3 lim n  3n  3 b) x  3  2 lim x c)      2 lim 2x 3 4x x x   3 2 x 1  x  x  x  1  2 3  2x  x  x 
Câu 14. (1 điểm) Cho hàm số f x  khi x  -1   x  1  2023 m  .x 1 khi x  -1 
Tìm m để hàm số f x liên tục tại x  1  . 0
Câu 15. (2,5 điểm) Cho hình chóp S.ABC có SA  SB  SC . Tam giác ABC vuông tại  0 ,
B BAC  60 ,AC  2a. Góc giữa đường thẳng SA và mặt phẳng ABC  bằng 0 30 . Gọi H,M lần lượt
là trung điểm của cạnh AC và SC .
a) Chứng minh rằng SH vuông góc với mặt phẳng ABC .
b) Tính góc giữa đường thẳng SA và BC .
c) Tính góc giữa đường thẳng MB và ABC 
d) Tính góc giữa đường thẳng SA và SBC . Câu 16 (1 điểm) 3 1 2x  1 3x a) Tính giới hạn lim 2 x0 x
b) Chứng minh phương trình   m 5 2 1
x  9mx  16x  m  0 có ít nhất hai nghiệm phân biệt với mọi m -------- Hết -------- 2
TRƯỜNG THPT THUẬN THÀNH SỐ 1
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II TỔ TOÁN NĂM HỌC 2022 - 2023 ------------- MÔN: Toán lớp 11
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giáo viên soạn đề: Cô Nguyễn Thị Tiếp
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
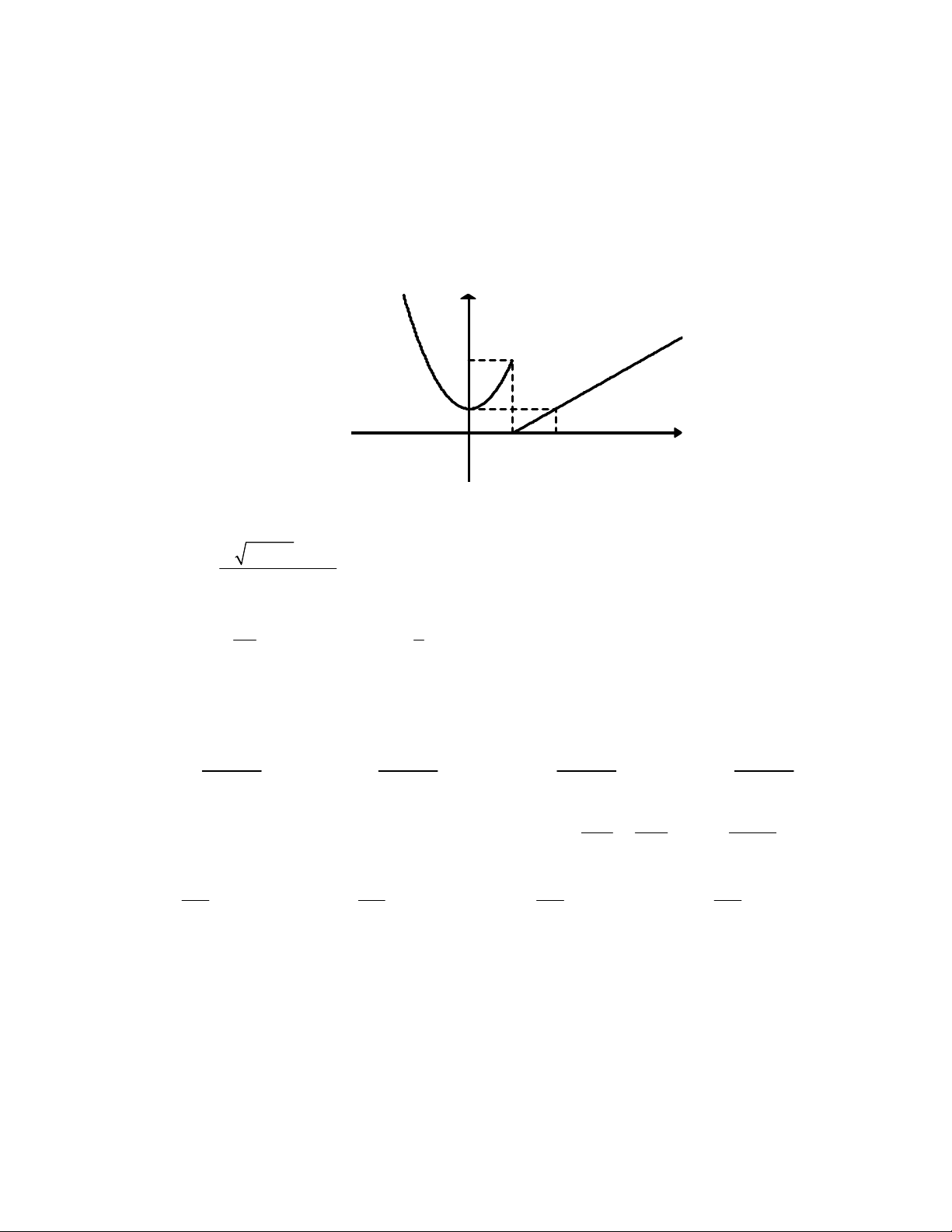
Câu 1. Cho hàm số f x xác định trên  và có đồ thị như hình vẽ. Hỏi hàm số f x không liên
tục tại điểm nào sau đây? y 3 1 x O 1 2 A. x  1. B. x  2 . C. x  3. D. x  0. 0 0 0 0 4x  1 1 Câu 2. Biết lim
 3, a   , tìm giá trị của a 2 x0 ax  2a     1 x 1 1 A. a   a  . C. a  6 . D. a  4 . 6 . B. 6
Câu 3. Cho cấp số nhân u có u  2 và u  54. Tính tổng 1000 số hạng đầu tiên của cấp số nhân đã n  2 5 cho. 1000 3 1 1000 1 3 1000 1 3 1000 3 1 A. S   B. S   C. S   D. S   1000 2 1000 4 1000 6 1000 6 1 1 1
Câu 4. Cho cấp số cộng u với u  11;u  13 . Tính tổng S    .. .  n  1 2 u u u u u u 1 2 2 3 99 100 9 10 10 9 A. S  B. S  C. S  D. S  209 211 209 200
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình thoi, cạnh bên SA  AB và SAvuông góc với BC
. Góc giữa hai đường thẳng SD và BC là? A. 45o B. 30o C. 0 60 D. 90o
Câu 6. Trong các khẳng định sau đây có bao nhiêu khẳng định là khẳng định đúng?
I. Nếu a  d và a / /thì d  
II. . Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường a và mặt phẳng (Q) thì mp(P)
song song hoặc trùng với mp(Q). 3
III. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường b và mặt phẳng (P) thì a song song song với b.
IV. Nếu đường thẳng d vuông góc với hai đường thẳng trong mặt phẳng thì d  . A. 1 B. 2 C. 3 D. 0
Câu 7. Trong các mệnh đề sau mệnh đề nào sai 1  2
 x  x  1  2 1 A. lim x  x   x   B. lim      x  2 1  2 x  2x  3   2  3x  2 3x  2 C. lim   D. lim  3 x 1  x  1 x 2  x
Câu 8. Có bao nhiêu giá trị m nguyên thuộc đoạn 20;20  2   để lim      mx 2m 3x x  A. 21 B. 22 C. 20 D. 41  12x 1 Câu 9. Cho hàm số  khi x  0 f(x)   x
. Mệnh đề nào sau đây đúng ? 1  3x khi x  0 
A. Hàm số liên tục trên  B. Hàm số gián đoạn tại x  3
C. Hàm số gián đoạn tại x  0 D. Hàm số gián đoạn tại x  1 f x1 3 f x 3f x 4
Câu 10. Cho hàm số f(x) liên tục trên  và lim  3. Tính lim 2 x 2  x  x  2 2 x 2  x  2x 27 A. 36 . B. 27 . C. . D. 4 . 2
Câu 11. Tìm tất cả các giá trị của tham số m để phương trình sau có nghiệm:  2 2m  5m   18 2 (x 1)  81 x  2 2x  3  0 1  1   1  A. m   . B. m  \ ;2   C. m  ;2  . D. m 0  ; ;2  . 2        2     2   
Câu 12. Bạn Vũ lớp 11A4 thả một quả bóng chuyền hơi từ tầng ba, độ cao 8m so với mặt đất và thấy
rằng mỗi lần chạm đất thì quả bóng lại nảy lên một độ cao bằng ba phần tư độ cao lần rơi trước. Biết quả
bóng chuyển động vuông góc với mặt đất. Khi đó tổng quảng đường quả bóng đã bay từ lúc thả bóng đến
khi quả bóng không máy nữa gần bằng số nào dưới đây nhất? A. 57m . B. 54m . C. 56m . D. 58m .
PHẦN II. TỰ LUẬN (7,0 điểm)
Câu 13. (2 điểm) Tính các giới hạn sau n n 2 7  9  2 x  3x  6  2x a) lim b) lim n n 1 3.8  9  x 2x  3 4 5  x  3 lim 3 3 2 2 lim ( x  2x  x  2x ) c) x 4  4  x d) x
Câu 14. (1,5 điểm) : Tìm a, b để hàm số sau liên tục trên tập xác định của chúng 2 a  x bx 5  khi x  1 f x   x 1 2  0 khi x  1  Câu 15. (3,0 điểm)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB đều, SC  a 2 , H là trung điểm
AB, M, N lần lượt là trung điểm SD, CB.
a) Chứng minh rằng CB  (SAB) , SH  (ABCD)
b) Chứng minh rằng DN  SC, AM  DN
c) Tính góc giữa SC, ABCD , AN, SBC 2
Câu 16. (0,5 điểm) Cho dãy số (u )thỏa mãn: u  1 ; 2 * u 
u a, n   . Biết rằng n 1 n 1  3 n lim 2 2 2
u  u  ..  u  2n  b . Tính giá trị của biểu thức T  ab 1 2 n  -------- Hết -------- 5
TRƯỜNG THPT THUẬN THÀNH SỐ 1
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II NĂM HỌC 2022 - 2023 TỔ TOÁN MÔN: Toán lớp 11 -------------
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giáo viên soạn đề: Cô Nguyễn Ngọc Anh
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm) 1 1 1 1 Câu 1. Hỏi , , ,
là bốn số hạng đầu của dãy số nào sau đây? 2 4 8 32 1 1 1 1 A. u  . B. u  . C. u  . D. u  . n 2n n 2n  1 n 2n n 2 n
Câu 2. Một công ty thực hiện việc trả lương cho các kĩ sư theo phương thức như sau: Mức lương của quý
làm việc đầu tiên cho công ty là 15 triệu đồng/quý và kể từ quý làm việc thứ hai mức lương sẽ được tăng
thêm 1,5 triệu đồng mỗi quý. Tổng số tiền lương một kĩ sư được nhận sau 3 năm làm việc cho công ty là A. 495 triệu đồng. B. 279 triệu đồng. C. 384 triệu đồng. D. 558 triệu đồng.   Câu 3. Cho hai vecto ,
u v trong không gian có độ dài lần lượt là a và 2a. Cosin của góc giữa hai vecto 1  
bằng . Tính tích vô hướng u.v : 2 A. 2 a B. a . C. 2 2a D. 2 a 3
Câu 4. Thêm 5 số xen giữa hai số 25 và 1 ta được một cấp số cộng có 7 số hạng. Số hạng thứ 50 là A. -169. B. 169. C. -171. D. 171.  3 x  , khi x  3
Câu 5. Giá trị thực của tham số m để hàm số f x    x 1 2 có giới hạn lim f x là x3   m  khi x  3  bao nhiêu? A. m  1 B. m  4 C. m  4  D. m  1
Câu 6. Cho hình chóp tứ diện OABC có O , A O ,
B OC đôi một vuông góc và OA  OB  , a OC  2a . Gọi
M là trung điểm của BC. Tính côsin góc giữa hai đường thẳng AB và OM. 10 5 1 3 A. B. C. D. 10 10 2 2
Câu 7. Cho hình chóp S.ABC có SA  SB  SC và A
 BC vuông tại C. Gọi H là hình chiếu vuông
góc của S lên ABC. Khẳng định nào sau đây đúng?
A. H là trung điểm của cạnh AB. B. H là trọng tâm của A  BC. C. H là trực tâm của A  BC.
D. H là trung điểm của cạnh AC.
Câu 8. Trong không gian cho đường thẳng  và điểm I. Có bao nhiêu mặt phẳng chứa điểm I và vuông
góc với đường thẳng ? A. 2. B. Vô số. C. Không có. D. 1. 6
Câu 9. Cho hình chóp S.ABCD có tất cả các cạnh đều bằng a. Gọi I và J lần lượt là trung điểm của SC và
BC. Số đo của góc IJ CD  , bằng A. 30°. B. 45°. C. 60°. D. 90°.
Câu 10. Cho hình chóp S.ABCD có đáy là hình thoi tâm ,
O SA  ABCD. Góc giữa SA và (SBD) là A.  ASD. B.  ASO. C.  ASB. D.  SA . B 2 x  x  3
Câu 11. Cho phương trình f(x)  0, f(x)  . Chọn đáp án đúng. 3x 1
A. Hàm số liên tục trên đoạn 0;1
  B. Hàm số liên tục trên R 1
C. Hàm số liên tục tại x  D. Phương trình luôn có nghiệm  3  ; 1   o 3   3 8x  11  x  7 a a Câu 12. Biết lim
 trong đó là phân số tối giản, a và b là các số nguyên dương. 2 x2 x  3x  2 b b Tổng 2a  b bằng A. 68 B. 69 C. 70 D. 71
PHẦN II. TỰ LUẬN (7,0 điểm)
Câu 13. (2 điểm) Tính giới hạn các hàm số sau: n 1 1 9   2 x  4x  3 a) lim b) lim 2n  3.9n 2 x 1  x 1 c)   d)     2 lim x 2x 3x x    2 lim x 2x x x   x  4 2  , khi x  0 
Câu 14. (2,0 điểm) Cho hàm số f x   x  m là tham số  2 1 m  x  2x  , khi x  0  4
Tìm m để hàm số liên tục tại x  0 .
Câu 15. (2,5 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA  (ABCD) . SA  a 2,AB  , a AD  a 3.
a) Chứng minh rằng tam giác SBC,SCD là các tam giác vuông.
b) Dựng AH là đường cao của tam giác SAD . Tính góc tạo bởi AH và SC .
c) Tính góc tạo bởi SB và (SAC).
d) Gọi M là trung điểm của SC . Tính góc tạo bởi AM và (ABCD).
Câu 16. (0,5 điểm) Chứng minh rằng phương trình 4 3 2
2x  mx  nx  p x  2023  0 có ít nhất 2
nghiệm với m,n, p   ---------Hết--------- 7
TRƯỜNG THPT THUẬN THÀNH SỐ 1
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II NĂM HỌC 2022 - 2023 TỔ TOÁN MÔN: Toán lớp 11 -------------
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giáo viên soạn đề: Thầy Nguyễn Thế Giang
Phần I: Trắc nghiệm khách quan( 7 điểm)
Câu 1: Cho tam giác đều ABC có cạnh bằng 2a . Người ta dựng tam giác đều A B C có cạnh bằng đường 1 1 1
cao của tam giác ABC ; dựng tam giác đều A B C có cạnh bằng đường cao của tam giác A B C và cứ tiếp 2 2 2 1 1 1
tục như vậy. Giả sử cách dựng trên có thể tiến ra vô hạn. Nếu tổng diện tích S của tất cả các tam giác đều
ABC,AB C ,A B C . . bằng 24 3 thì a bằng: 1 1 1 2 2 2 A. 4 3 B. 3 C. 6 D. 3 3
Câu 2: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AB  a . SA vuông góc với
mặt phẳng ABC và SA  a . Gọi  là góc giữa SB và SAC . Tính . A. 0   30 . B. 0   60 . C. 0   45 . D. 0   90 . 12n3 Câu 3: Biết lim
 4 với a là tham số. Khi đó 2 a a bằng 3 an  2 A. 4 B. 6 C. 2 D. 0
Câu 4: Cho hình tứ diện ABCD . Gọi M,N lần lượt là trung điểm của AB và CD , I là trung điểm của
đoạn MN . Mệnh đề nào sau đây sai?
 1      MN  AD CB 1 B. AN  AC  AD 2   2   A.   
     C. MA  MB  0
D. IA  IB  IC  ID  0
Câu 5: Trong các mệnh đề sau mệnh đề nào sai 1  2
 x  x  1  2 1 A. lim x  x   x   B. lim      x  2 1  2 x  2x  3   2  3x  2 3x  2 C. lim   D. lim  3 x 1  x  1 x 2  x
Câu 6: Cho hình lập phương ABCD.AB C  D
  . Khẳng định nào sau đây là khẳng định sai?
A. Góc giữa hai đường thẳng B D
  và AA bằng 60. B. Góc giữa hai đường thẳng AC và B D   bằng 90.
C. Góc giữa hai đường thẳng AB và D C
 bằng 45. D. Góc giữa hai đường thẳng D C  và AC  bằng 60. n n 2 2017  2019  Câu 7: Tính giới hạn lim n n 1 3.2018  2019  8 1  1 A. B. C. 2  019 D. 0 2019 2019
Câu 8: Có bao nhiêu giá trị m nguyên thuộc đoạn 20;20  2   để lim      mx 2m 3x x  A. 21 B. 22 C. 20 D. 41
Câu 9: Hàm số nào sau đây không liên tục tại x  2 2x  6 1 x 3x 1 A. y  B. y  C. y  D. y  2 x  2 x  2 x  2 x  22 f(x)  1  2x xf x2 Câu 10: Cho lim  1 . Tính I  lim x 1  x 1 x 1  x 1 A. I  5 B. I  4  C. I  4 D. I  5  7
Câu 11: Cho a ,b là các số dương. Biết lim x ax  x bx  
.Tìm giá trị lớn nhất x  2 3 3 2 9 27 5 27 của ab 49 59 43 75 A. 18 B. 34 C. 58 D. 68
Câu 12: Cho hàm số y  f x liên tục trên đoạn 1;5   và f  
1  2, f 5  10 . Khẳng định nào sau đây đúng ?
A. Phương trình f x  6 vô nghiệm
B. Phương trình f x  7 có ít nhất một nghiệm trên khoảng 1;  5
C. Phương trình f x  2 có hai nghiệm x  1,x  5
D. Phương trình f x  7vô nghiệm
PHẦN II. TỰ LUẬN (7,0 điểm)
Câu 1(1,5 điểm): Cho cấp số cộng u cóu  15,u  60 .Tìm số hạng đầu tiên ,công sai và tính n  5 20
tổng của 20 số hạng đầu tiên của cấp số cộng.
Câu 2 (2 điểm): Tìm các giới hạn 2 x  2x a) Tính lim b)  2 lim 9n  2n 1  3n. 2 x 2  x  3x  2  
Câu 3(1 điểm): Cho tứ diện ABC .
D Trên cạnh AD lấy điểm M sao cho AM  2MD và trên cạnh BC     
lấy điểm N sao cho NB  2
 NC. Chứng minh rằng ba vectơ A , B CD và MN đồng phẳng. Câu 4. (2,0 điểm) 9
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a 3 và AC  2a . Biết
SA  ABCD, góc giữa đường thẳng SB và mặt phẳng ABCD bằng 0 60 .
1) Chứng minh BC  SAB.
2) Gọi G là trọng tâm tam giác SAB . Tính diện tích thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng CDG theo a.
Câu 5(0,1 điểm): Tìm tất cả các giá trị của tham số m để phương trình  2 2m  5m   18 2 (x 1)  81
x  2 2x  3  0 có nghiệm. -----------Hết------------ 10
TRƯỜNG THPT THUẬN THÀNH SỐ 1
ĐỀ THAM KHẢO KIỂM TRA GIỮA HỌC KÌ II NĂM HỌC 2022 - 2023 TỔ TOÁN MÔN: Toán lớp 10 -------------
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Giáo viên soạn đề: Cô Nguyễn Thị Thùy Dương
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Câu 1. Cho cấp số cộng u có u  1 và công sai d  2. Tổng S  u  u  u .. ..  u bằng: n  1 10 1 2 3 10 A. S  21. B. S  19 C. S  110. D. S  100. 10 10 10 10
Câu 2. Trong các giới hạn sau đây, giới hạn nào bằng 0? 3 3  2n 2 2n  3 3 2n  3n 2 4 2n  3n A. lim . B. lim . C. lim . D. lim . 2 2n 1 3 2n  4 2 2n 1 4 2 2n  n 2 4 2n
Câu 3. Tính tổng S  1       . 3 9 3n A. S  3. B. S  4. C. S  5. D. S  6.
Câu 4. Cho cấp số nhân u có công bội q. Mệnh đề nào sau đây đúng? n  u  u A. k 1 u u .q   . B. k 1 k 1 u    . k 1 k 2 10n 1
C. S  9  99  999  ..  999. .9 D. S   . 9
Câu 5. Cho hai đường thẳng a, b và hai mặt phẳng (P), (Q). Mệnh đề nào sau đây đúng? a  P a  P  A.  B. b P    a//b.     a // .b b P   a b    P//Q a //P  C.   D.   a// Q . a  P a //Q.  P  Q   
Câu 6. Cho tứ diện ABCD có AB, BC, CD đôi một vuông góc với nhau và AB a , BC  b, CD  c . Độ dài đoạn thẳng AD bằng A. 2 2 2 a  b  c . B. 2 2 2 a  b  c . C. 2 2 2 a  b  c . D. 2 2 2 a b  c .
Câu 7. Hàm số nào dưới đây liên tục trên  ? 3x 1 A. y  . B. y  3  tanx. 2 1 x 11 4  x 3  2x C. y  . D. y  . 2 2  1  x 1  sinx 2 x  1 Câu 8. Cho hàm số f(x) 
. Hàm số f(x)liên tục trên khoảng nào dưới đây? 2 x  5x  6 A. ( 3  ; )  B. ( 3  ;2) C. ( ;  3) D. (2;3)
Câu 9. Cho tứ diện ABCD có G là trọng tâm tam giác BCD . Khẳng định nào sau đây là khẳng định đúng? 
2    
1    A. AG  AB  AC  AD AG  AB  AC  AD 3   3   B. 
1    
2   
C. AG   AB  AC  AD
D. AG   AB  AC  AD 3   3   Câu 10. Cho hình hộp ABC .
D A'B 'C 'D ' (tham khảo hình vẽ). A' D' B' C' A D B C
Mệnh đề nào sau đây sai ?
A. Hai mặt phẳng A'BD và CB 'D ' cắt nhau.
B. Hai mặt phẳng ABCD,A'B 'C 'D ' song song với nhau.
C. Đường thẳng A'B ' song song với mặt phẳng CC 'D 'D.
D. Đường thẳng A'D ' song song với mặt phẳng ABCD. 2x  3  3 a a Câu 11. Biết giá trị lim
 với a,b là các số nguyên dương và phân số tối giản. Tính giá x3 x  3 b b trị 2 2 a b ? A. 10 B. 13 C. 17 D. 5
Câu 12. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O . Biết SO  ABCD, SO=a 3 và
đường tròn ngoại tiếp đáy ABCD có bán kính bằng a 2 Góc giữa mặt phẳng SCD và mặt đáy là: A. 0 75 B. 0 60 C. 0 30 D. 0 45
PHẦN II. TỰ LUẬN (7,0 điểm) Câu 13. (2,5 điểm) n n 1 3  2.5  3 2 x  4  2 a) lim b) lim n 1 2   5n x 2  2 4  2x  8 Câu 14. (2,0 điểm) 12  2  x  8  3  ,x  1  a) Cho hàm số f x 2   x  4x  3 . 
Tìm giá trị của a để f x liên tục tại x  1. 1 2  cos x   a  x , x  1 6
b) Một du khách vào trường đua ngựa đặt cược, lần đầu đặt 20000 đồng, mỗi lần sau tiền đặt gấp đôi lần
tiền đặt cọc trước. Người đó thua 9 lần liên tiếp và thắng ở lần thứ 10. Hỏi du khác trên thắng hay thua bao nhiêu?
Câu 15. (2,5 điểm) Cho hình chóp S.ABCD có đáy là hình vuông tâm O, cạnh a. Biết SA  (ABCD) và SA = a.
a) Chứng minh rằng BC  (SAB) và CD  (SAD).
b) Chứng minh rằng BD  SC .
c) Gọi E là trung điểm của cạnh SC. Chứng minh rằng AE  SO và AE  (SBD).
d) Tính góc tạo bởi đường thẳng AC và mặt phẳng (SCD). -------- Hết -------- 13