Đề thi chọn HSG tỉnh Toán 11 năm 2017 – 2018 sở GD&ĐT Quảng Bình

SỞ GD&ĐT QUẢNG BÌNH KỲ THI CHỌN HSG TỈNH NĂM HỌC 2017-2018
Khóa ngày 22 tháng 3 năm 2018 ĐỀ CHÍNH THỨC Môn thi: TOÁN
Họ và tên:………………….. LỚP 11 THPT
Thời gian: 180 phút (không kể thời gian giao đề)
SỐ BÁO DANH:……………
Đề gồm có 01 trang. Câu 1 (2.0 điểm)
sin 2x  cos 2x  3sin x  cos x  2 a. Giải phương trình:  0. sin x 2 5 3.  x y  4   2 2 3 y  x 
b. Giải hệ phương trình:  4 2 2 3
 5. x y  y  x  Câu 2 (2.0 điểm) 4
8x  8  x  3x  6
a. Tính giới hạn: lim . x  x  2 1 1
b. Một hộp đựng chín quả cầu được đánh số từ 1 đến 9. Hỏi phải lấy ra ít nhất bao 5
nhiêu quả cầu để xác suất có ít nhất một quả cầu ghi số chia hết cho 4 phải lớn hơn . 6 Câu 3 (2.0 điểm)
a. Cho dãy số u được xác định bởi: n  2 1 n  n  2 u  5 , u  u  ;n  1. 1 n 1  n 3 2 2
n  3n  2n Tính giới hạn lim . n u . n 
b. Tìm tất cả các số nguyên dương n sao cho 2n 2
3  3n  7 là một số chính phương. Câu 4 (3.0 điểm) Cho hình hộp ABC .
D A' B 'C ' D ' . Gọi G là trọng tâm của tam giác BC ' D .
a. Xác định thiết diện của hình hộp ABC .
D A' B 'C ' D ' khi cắt bởi mặt phẳng
 ABG  .Thiết diện đó là hình gì?
b. Hai điểm M , N lần lượt thuộc hai đoạn thẳng AD, A'C sao cho MN song song 1 CN
với mặt phẳng  BC ' D  , biết AM  AD . Tính tỉ số . 4 CA'
Câu 5 (1.0 điểm) Cho a, ,
b c là các số thực dương. Chứng minh rằng : 2a 2b 2c 3 3 3    2
4a  4b  c
4b  4c  a
4c  4a  b
......................................HẾT.........................................
SỞ GD&ĐT QUẢNG BÌNH KỲ THI CHỌN HSG TỈNH NĂM HỌC 2017-2018
Khóa ngày 22 tháng 3 năm 2018 HƯỚNG DẪN CHẤM Môn thi: TOÁN LỚP 11 THPT
Đáp án này gồm có 06 trang YÊU CẦU CHUNG
* Đáp án chỉ trình bày một lời giải cho mỗi bài. Trong bài làm của học sinh yêu cầu
phải lập luận lôgic chặt chẽ, đầy đủ, chi tiết và rõ ràng.
* Trong mỗi bài, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với
những bước giải sau có liên quan. Ở câu 4 nếu học sinh không vẽ hình hoặc vẽ hình sai thì cho điểm 0.
* Điểm thành phần của mỗi bài nói chung phân chia đến 0,25 điểm. Đối với điểm
thành phần là 0,5 điểm thì tuỳ tổ giám khảo thống nhất để chiết thành từng 0,25 điểm.
* Học sinh có lời giải khác đáp án (nếu đúng) vẫn cho điểm tối đa tuỳ theo mức điểm của từng bài.
* Điểm của toàn bài là tổng (không làm tròn số) của điểm tất cả các bài. Câu Nội dung Điểm
sin 2x  cos 2x  3sin x  cos x  2 a. Giải phương trình:  0. 1,0 sin x
Điều kiện xác định: sin x  0  x  k . 
Phương trình  sin 2x  cos 2x  3sin x  cos x  2  0  2sin .
x cos x  cos x   2
1  2sin x  3sin x  2  0
 cos x 2sin x   1   2
2sin x  3sin x   1  0 0,25  2sin x  
1 cos x  sin x   1  0  1 sin x    2
cos x  sin x 1    x   k 2 1  Câu 1 6 sin x    0,25 (2,0 điểm) 2 5 x   k 2  6 x  k 2    1 sin x cos x 1 sin x           0,25  4  2 x   k 2  2
Đối chiếu điều kiện, nghiệm của phương trình là:  5  0,25 x 
 k 2 ; x   k 2 ;  x   k 2 .  k  . 6 6 2 2 5 3  x y  4   2 2 3 y  x 
b. Giải hệ phương trình sau:  4 2 2 3
 5 x y  y  x  1,0 Ta thấy  ;
x y   0;0 là một nghiệm của hệ phương trình 0,25 Với  ;
x y   0;0 , ta có: 2 2 0,25 x y   2 2 y  x  2 2
y  x    2 2 x  y  2 2 15 4 4
x  4 y   0  y  2  x
TH1: y  2x , ta có: 3 2 5
3 x .32.x  4 2 2 4x  x  3 2 5 2 
x .32.x  4x 7 6
 32.x  64.x  x  2  y  4 (vì  ;
x y   0;0 ) 0,25
Do đó hệ phương trình có nghiệm  ; x y   2;4 TH2: y  2  x , ta có: 3 2 5 3 
x .32.x  4 2 2 4x  x  3 2 5 2
  x .32.x  4x 7 6  3
 2.x  64.x  x  2
  y  4 (vì  ;
x y   0;0 ) 0,25
Do đó hệ phương trình có nghiệm  ; x y    2  ;4
Vậy hệ phương trình đã cho có 3 nghiệm: 0;0 , 2;4 ,  2  ;4 . 4
8x  8  x  3x  6 a. Tính : lim 1,0 x  x  2 1 1 Ta có: 4
8x  8  x  3x  6
 8x 8 x 3 4
x  4x  3    0,25 lim  lim    x  x  2 1 x   x  2 1  x  2 1 1 1   
8x  8   x  3 4 x  4x  3  lim  lim x  x  2 1 x  x  2 1 1 1 2 0,25 2 2
x    x    x  
1  x  2x  3 8 8 3   lim  lim
x  x  2
1  8x  8   x  3 x  x  2 1 1 1 2 2 2  x    x  
1  x  2x  3 1   lim  lim
x  x  2
1  8x  8  x  3 x  x  2 1 1 1 Câu 2 0,25 (2,0 điểm) 1   lim  lim 2
x  2x  3 x 1  x 1
8x  8  x  3  1  49   6   0,25 8 8
b. Một hộp đựng chín quả cầu được đánh số từ 1 đến 9. Hỏi phải
lấy ra ít nhất bao nhiêu quả cầu để xác suất có ít nhất một quả 1,0 5
cầu ghi số chia hết cho 4 phải lớn hơn 6
C Giả sử ta lấy ra x quả cầu 1  x  9, x   , số cách chọn x quả cầu
ừ từ 9 quả cầu trong hộp là x
C nên số phần tử của không gian mẫu là 9  x n  C . 9 0,25
Gọi A là biến cố ‘‘trong số x quả cầu lấy ra, có ít nhất một quả cầu
ghi số chia hết cho 4’’, thế thì biến cố đối của A là A : ‘‘trong số x
quả cầu lấy ra, không có quả cầu nào ghi số chia hết cho 4’’.
Số cách chọn tương ứng với biến cố A là   x n A  C . 7 n A x C 9  x 8  x x 17x  72 0,25 7    2
Ta có: P  A     n x C 72 72 9 2 5 x 17x  72 1
Do đó: P  A  1 P A   P A   . 6 72 6 0,25 hay 2
x 17x  60  0  5  x  12
Vì 1  x  9, x   nên 6  x  9, x   .
Do đó giá trị nhỏ nhất của x là 6. 0,25
Vậy số quả cầu phải lấy ra ít nhất mà ta phải tìm là 6 quả cầu.
a.Cho dãy số u được xác định bởi: n  2 1 n  n  2 u  5 , u  u  ;n  1 . 1.0 1 n 1  n 3 2 2
n  3n  2n Tìm lim . n u n  Ta có: 1
(n 1)(n  2) 1 2 1 u  u   u   n 1  n n 2
n(n  1)(n  2) 2 n  1 n 0.25 2 1  2  Hay: u   u  n 1    n  1 2 n  n  2 1
Đặt v  u 
;n  1 . Khi đó ta có dãy số v v  v  v n  n  , 3; ; 1 n n 1 n 1  n n 2 1
là một cấp số nhân có v  3, công bội q  . 0.25 1 2 1 3 2 3n Nên v  3. hay u   ;n  1  . n u   2 . n n 1 2  n n 1  n n 1 2 n 2 
Bằng quy nạp ta chứng minh được n 1  2 2  n ; n   1 . (1)
Thậy vậy: Với n  1, n  2, n  3 , (1) đúng 
Giả sử (1) đúng với n  k,(k  3) tức 1 2
2k  k đúng 0.25
Ta chứng minh (1) đúng với n  k  1, Thật vậy: k2 k 1  2 2 2  2.2
 2.k  (k  1) , k   3 3n 12 3n Suy ra: 0   . Từ đây suy ra: lim  0 . 1 2n n 1 2n 0.25  3n  Khi đó lim . n u    . n  lim 2 2  n 1    2 
b. Tìm tất cả các số nguyên dương n sao cho 2n 2 3  3n  7 là 1.0 Câu 3 một số chính phương.
(2,0 điểm) Nếu 2n 2 2
3  3n  7  b với b    thì 2 2 3 n b  hay 3n b  . Điều này 0.25 chứng tỏ: 3n b   1. Do đó: n      n  2 2 2 2 2 3 3 7 3 1  3 n  2.3n n b  1. Suy ra n 2 2.3  3.n  6 ( )  0.25 Nếu n  3 thì ( )  không xảy ra vì: n
2.3n  2.1 2  2 0 1 2 2
C  C .2  C .2  .. n n n .  n(n 1) 2   2 1  2n  .2  ...    2  0.25 2 2
 2  4n  4n  4n  3n   2 n  2 2 2
 3n  11  3n  6
Do đó n  1hoặc n  2 .
Khi n  1ta tính được 2n 2
3  3n  7  19 không phải là số chính phương 0.25
Khi n  2 ta tính được 2n 2
3  3n  7  100 là số chính phương. Kết luận: n  2 Cho hình hộp ABC .
D A' B 'C ' D ' . Gọi G là trọng tâm của tam giác BC ' D 3,0 .
a. Xác định thiết diện của hình hộp ABC .
D A' B 'C ' D ' khi cắt bởi 1,5
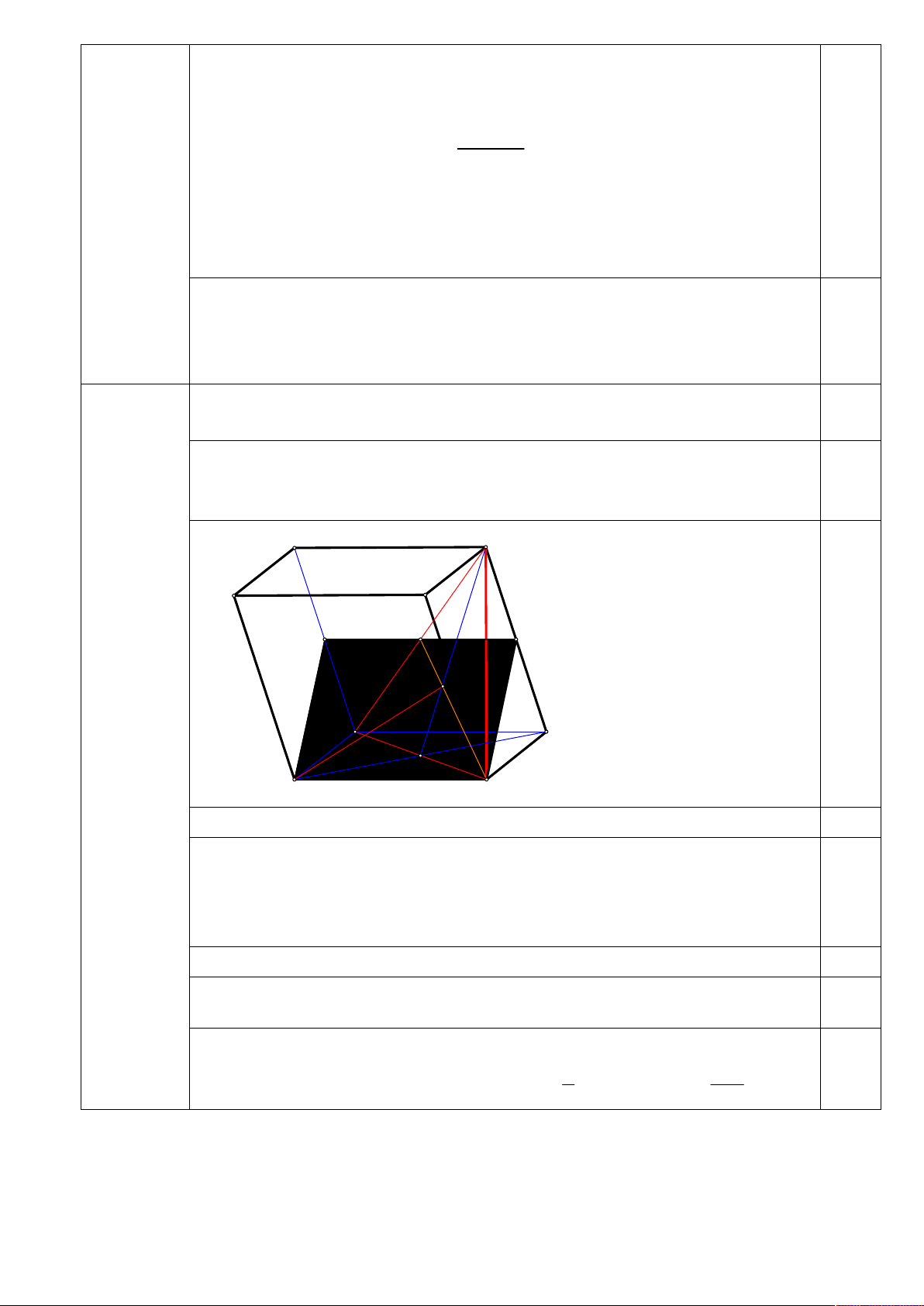
mặt phẳng  ABG  .Thiết diện đó là hình gì? D' C' B' A' F I E 0,5 G D Câu 4 C (3,0 điểm) O A B
Trong mặt phẳng  BC ' D  kéo dài BG cắt C ' D tại I . 0,25 Khi đó: 
 ABG    CDD 'C '   Ix 
 AB   ABG ,CD   CDD 'C '   Ix  CD 0,25  AB  CD 
Từ đó, trong  CDD 'C '  kẻ Ix  CD cắt CC ', DD ' lần lượt tại E, F 0,25
Vậy thiết diện cần tìm là hình bình hành ABEF (Vì EF  CD  AB 0,25
và EF song song với AB )
b. Hai điểm M , N lần lượt thuộc hai đoạn AD, A'C sao cho MN song 1 CN 1,5
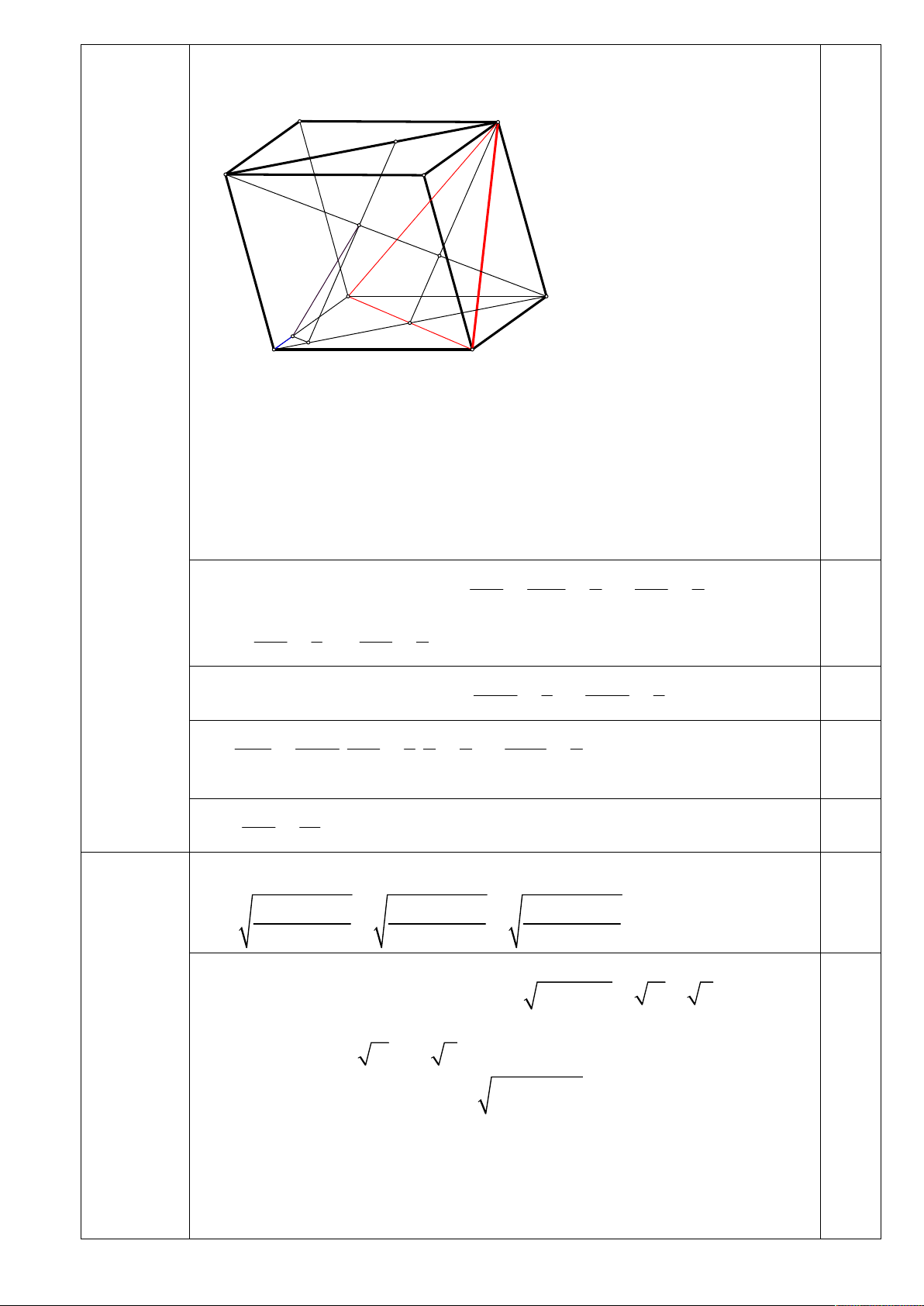
song với mặt phẳng  BC ' D  , biết AM  AD . Tính tỉ số . 4 CA' D' C' L A' B' N G C D M O K A B
Gọi O  AC  BD . Ta thấy A'C đi qua G .
Khi đó, qua M kẻ đường thẳng song song với BD và cắt AC tại K . 0,25
Trong mặt phẳng  ACC ' A'  , gọi L  KN  A'C ' , ta có:
MN   BC D    MNK    BC D   KN   BC D   ' ' '
 KN  OC ' 0,25
MK   BC ' D  AK AM 1 KO 3
Mặt khác, theo giả thiết, ta có:     AO AD 4 AO 4 0,25 KO 3 KC 7   và  AC 8 AC 8 LC ' 3 A' L 5
Vì KO  LC ', AC  A'C ' nên    0,25 A'C ' 8 A'C ' 8 A' L A' L AC 5 8 5 A' N 5 Mà  .  .    KC A'C ' KC 8 7 7 NC 7 0,25 CN 7 Vậy  . 0,25 CA' 12 Cho a, ,
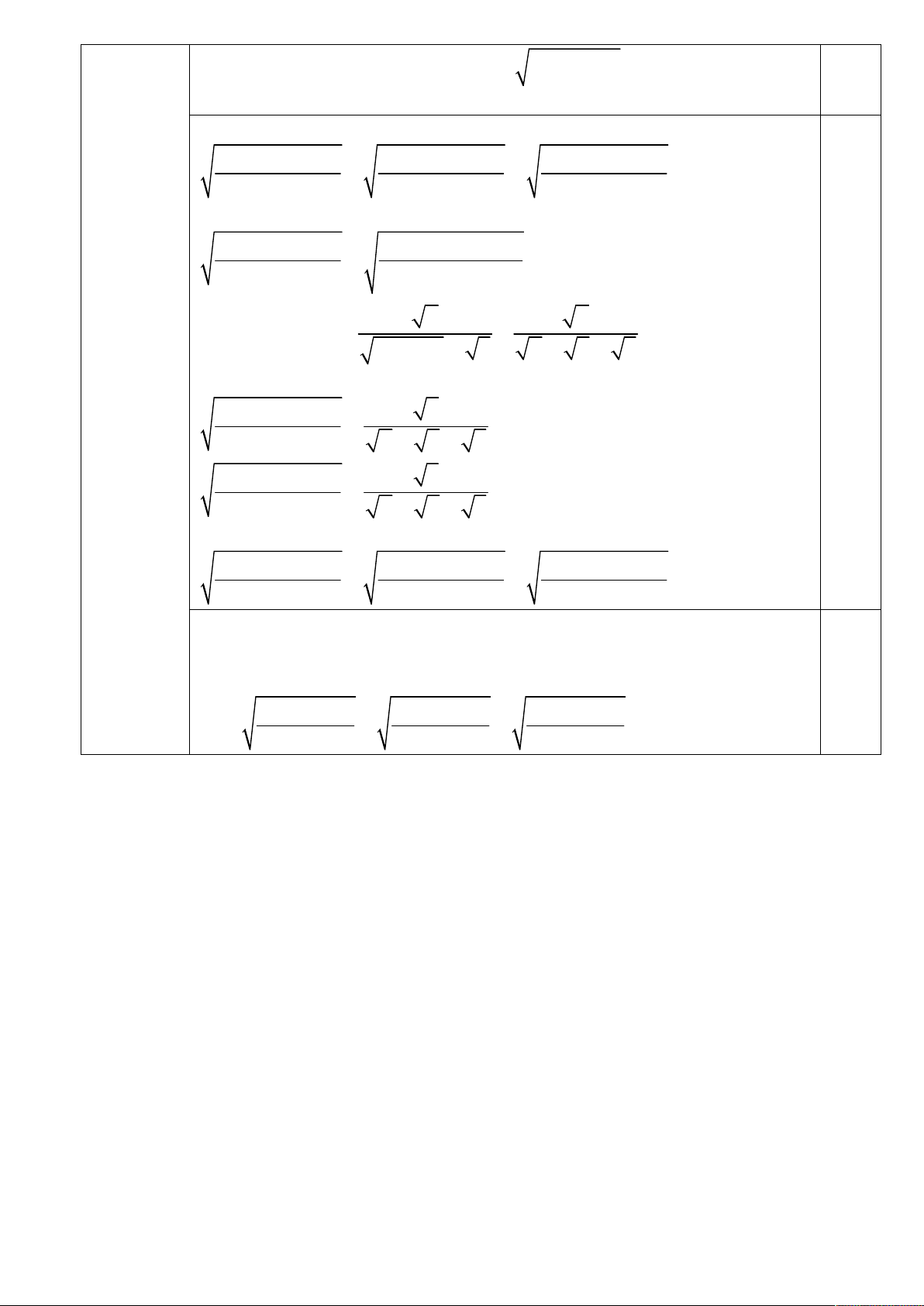
b c là các số thực dương. Chứng minh rằng : 2a 2b 2c 1,0 3 3 3    2 (1)
4a  4b  c
4b  4c  a
4c  4a  b
Ta chứng minh bổ đề sau:
Cho các số thực dương m, n khi đó: 3 3 3 4(m  n)  m  n (2) ,
Dấu ‘=’ xảy ra khi và chỉ khi m = n. Thật vậy: Đặt 3 3
x  m, y  n ; (x, y  0) .
Bất đẳng thức (2) được viết lại  3 3
3 4 x  y   x  y . Ta xét: Câu 5 3 3 3 3 2 2 3 (1.0 điểm)
4(x  y )  (x  y)  3 x  x y  xy  y  0,25
 3 x  y 2 2 x  y 
 3 x  y2  x  y  0; x  , y  0 Nên ta có: 3 3 3
4(x  y )  (x  y) hay  3 3
3 4 x  y   x  y
hay bất đẳng thức (2) ở bổ đề được chứng minh xong.
Bất đẳng thức đã cho tương đương với a b c 3 3 3    1
16a  16b  4c
16b  16c  4a
16c  16a  4b
Sử dụng bất đẳng thức (2) ở bổ đề trên ta có: a a 3  3
16a  16b  4c
44a  4b  c 3 3 a a   3 3 3 3
3 4(a  b)  c
a  b  c 0,25 Tương tự: 3 b b 3  ; 3 3 3
16b  16c  4a
a  b  c 3 c c 3  3 3 3
16c  16a  4b
a  b  c 0.25 Từ đây ta có: a b c 3 3 3    1 (3)
16a  16b  4c
16b  16c  4a
16c  16a  4b
Đẳng thức (3) xảy ra khi 4a  4b  c, 4b  4c  a, 4c  4a  b nên
8(a  b  c)  a  b  c  a  b  c  0 mâu thuẫn. Chứng tỏ dấu ‘‘=’’ không xảy ra. 0,25 2a 2b 2c Vậy 3 3 3    2
4a  4b  c
4b  4c  a
4c  4a  b