Đề thi chọn HSG Toán 11 năm 2021 – 2022 sở GD&ĐT Quảng Bình

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề thi chọn học sinh giỏi môn Toán 11 năm học 2021 – 2022 và chọn đội dự tuyển dự thi chọn học sinh giỏi Quốc gia môn Toán năm học 2022 – 2023 sở Giáo dục và Đào tạo tỉnh Quảng Bình 

23 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

13 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
SỞ GD&ĐT QUẢNG BÌNH
ĐỀ CHÍNH THỨC
KỲ THI CHỌN HSG LỚP 11 NĂM HỌC 2021-2022
VÀ CHỌN ĐỘI DỰ TUYỂN DỰ THI CHỌN HSG
QUỐC GIA NĂM HỌC 2022-2023
Khóa ngày 25 tháng 4 năm 2022
Môn thi: TOÁN
SỐ BÁO DANH:……………
VÒNG 1
Thời gian: 180 phút (không kể thời gian giao đề)
Đề gồm có 01 trang v 05 câu
Câu 1 (2,0 điểm).
a. Giải phương trình
22
2sin 2sin tan
4
x x x



.
b. Chứng minh rằng phương trình
2 2022 2 2
20m x x x m
luôn có ít nhất hai nghiệm
phân biệt với mọi tham số m.
Câu 2 (2,0 điểm).
a. Cho
n
là số nguyên dương thỏa mãn
12
1. 2. ... . 16
n
n n n
C C nC n
. Tìm hệ số của số
hạng chứa
7
x
trong khai triển của nhị thức
,
0x
.
b. Cho cấp số cộng
n
u
có các số hạng đều là số nguyên và công sai
d
là một số
dương. Biết rằng
20
0um
và
17
m
u
. Tính
2022
u
.
Câu 3 (2,0 điểm).
a. Tính giới hạn
3
2
0
1 2 1 3
lim .
x
xx
x
b. Cho dãy số
n
u
xác định bởi:
1
9u
và
1
3 5 22
nn
n u n u
với mọi
1n
.
Tính giới hạn
2
2021
lim .
25 4 2022
n
u
nn
Câu 4 (3,0 điểm). Cho hình chóp
.S ABCD
có đáy
ABCD
là hình chữ nhật,
SA
vuông góc
với mặt phẳng
ABCD
và
,,SA a AB b AD c
. Gọi
H
là hình chiếu vuông góc của
A
lên mặt phẳng
SBD
.
a. Trong trường hợp
7, 1SA AB AD
, gọi
P
là mặt phẳng đi qua
A
và vuông
góc với
SC
. Hãy xác định thiết diện của hình chóp
.S ABCD
khi cắt bởi mặt phẳng
P
và tính diện tích thiết diện đó.
b. Chứng minh rằng
H
là trực tâm của tam giác
SBD
.
c. Chứng minh rằng
3
. . .
2
HBD HSD HSB
abc
a S b S c S
, ở đây kí hiệu
XYZ
S
là diện tích
của tam giác
XYZ
.
Câu 5 (1,0 điểm). Gọi
S
là tập hợp tất cả các số nguyên dương nhỏ hơn 1000. Một số
thuộc
S
được gọi là số “thú vị” nếu số đó là hợp số và không chia hết cho ba số
2; 3; 5
.
Chọn ngẫu nhiên một số từ
S
, tính xác suất để số được chọn là số “thú vị”.
-------------HẾT -------------
1
SỞ GD&ĐT QUẢNG BÌNH
HƯỚNG DẪN CHẤM
KỲ THI CHỌN HSG LỚP 11 NĂM HỌC 2021-2022
VÀ CHỌN ĐỘI DỰ TUYỂN DỰ THI CHỌN HSG
QUỐC GIA NĂM HỌC 2022-2023
Khóa ngày 25 tháng 4 năm 2022
Môn thi: TOÁN
VÒNG 1
Đp n ny gồm có 06 trang
YÊU CẦU CHUNG
* Đp n chỉ trình by một lời giải cho mỗi câu. Trong bi lm của học sinh yêu cầu
phải lập luận lôgic chặt chẽ, đầy đủ, chi tiết v rõ rng.
* Trong mỗi câu, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với
những bước giải sau có liên quan. Ở câu 4 nếu học sinh không vẽ hình hoặc vẽ hình sai thì
cho điểm 0.
* Điểm thnh phần của mỗi câu nói chung phân chia đến 0,25 điểm. Đối với điểm
thnh phần l 0,5 điểm thì tuỳ tổ gim khảo thống nhất để chiết thnh từng 0,25 điểm.
* Học sinh có lời giải khc đp n (nếu đúng) vẫn cho điểm tối đa tuỳ theo mức điểm
của từng câu.
* Điểm của ton bi l tổng (không lm tròn số) của điểm tất cả cc câu.
Câu
Ni dung
Đim
1a
Giải phương trình
22
2sin 2sin tan
4
x x x



.
ĐK:
2
xk

2
2
1 cos 2 2sin tan
2
1 sin2 2sin tan
pt x x x
x x x



0.25
22
cos 2sin cos 2sin cos sin
sin cos 2sin cos sin cos 0
sin cos 1 sin2 0
x x x x x x
x x x x x x
x x x
0.25
sin cos 0
1 sin2 0
tan 1
sin2 1
xx
x
x
x



0.25
4
4
x k TM
x k TM

Vậy phương trình có nghiệm là
4
xk
và
4
xk

.
0.25
2
1b
Chứng minh rằng phương trình
2 2022 2 2
20m x x x m
luôn có
ít nhất hai nghiệm phân biệt với mọi tham số m.
TH1:
0m
Phương trình trở thành
2
0
20
1
2
x
xx
x
(đúng).
0.25
TH2:
0m
Xét hàm số
2 2022 2 2
( ) 2f x m x x x m
liên tục trên
nên nó liên tục trên các đoạn
1;0 , 0;1
.
0.25
Lại có:
2
1 3, 0 , 1 1f f m f
.
0.25
Nên
2
1 . 0 3 0,f f m
2
0 . 1 0,f f m m
.
Suy ra trên mỗi khoảng
1;0 , 0;1
phương trình
2 2022 2 2
20m x x x m
luôn có ít nhất 1 nghiệm.
Vậy phương trình đã cho luôn có ít nhất hai nghiệm phân biệt với
mọi
m
.
0.25
2a
Cho
n
là số nguyên dương thỏa mãn
12
1. 2. ... . 16
n
n n n
C C nC n
.
Tìm hệ số của số hạng chứa
7
x
trong khai trin của nhị thức
21
2
2
n
x
x



,
0x
.
Đặt
12
1. 2. ... .
n
n n n
S C C nC
.
Sử dụng công thức
k n k
nn
CC
với
0;1;...;kn
, ta viết lại tổng
S
như
sau:
0 1 2 1
1 2 ... 1
n
n n n n
S nC n C n C C
.
Suy ra
0 1 2
2 ...
n
n n n n
S n C C C C
.
1
2 .2 .2 .
nn
S n S n
0.25
Nên
16Sn
hay
1
.2 16 5
n
n n n
.
0.25
Lúc đó:
2 1 11
11
11
2 2 2
11
0
2 2 2
nk
k
k
k
x x C x
x x x
11
22 3
11
0
2
k
kk
k
Cx

.
0.25
Ta tìm
k
sao cho
22 3 7 5kk
.
Vậy hệ số cần tìm là:
5
5
11
2 14784.C
0.25
2b
Cho cấp số cng
n
u
có các số hạng đều là số nguyên và có công sai
d
là mt số dương. Biết rằng
20
0um
và
17
m
u
. Tính
2022
u
.
Từ giả thiết:
20 1
19m u u d
và
1
17 ( 1)
m
u u m d
.
0.25
17 19 1m d m d
20 17 3
20
11
d
m
dd

.
0.25
Vì
m
và
0d
nên
1d
là ước số lớn hơn 1 của 3 hay
13d 
.
Ta được
2, 19dm
.
0.25
Vậy
2022
4023u
.
0.25
3
3a
Tính giới hạn
3
2
0
1 2 1 3
lim
x
xx
x
.
Ta có
3
3
2 2 2
0 0 0
1 2 1 1 1 3
1 2 1 3
lim lim lim
x x x
x x x x
xx
x x x

0.25
23
2
00
22
2
3
3
1 2 1 1 1 3
lim lim
1 2 1
1 1 1 3 1 3
xx
x x x x
x x x
x x x x x





0.25
00
22
3
3
13
lim lim
1 2 1
1 1 1 3 1 3
xx
x
xx
x x x x






0.25
1 3 1
2 3 2
.
Vậy
3
2
0
1 2 1 3 1
lim
2
x
xx
x
.
0.25
3b
Cho dãy số
n
u
xác định bởi:
1
9u
và
1
3 5 22
nn
n u n u
với mọi
1n
. Tính giới hạn
2
2021
lim
25 4 2022
n
u
nn
.
Với
*
n
, đặt
11
nn
vu
, khi đó
1
20v
và
1
22 3 11 5 11
nn
n v n v
.
1
35
nn
n v n v
.
0.25
1 1 2
1
5 ( 5)( 4) ( 5)( 4)
3 ( 3)( 2) ( 2)( 1)
( 5)( 4)
( 5)( 4).
5.4
n n n n
n n n n n
v v v v
n n n n n
nn
v n n

0.25
Nên
2
( 4)( 3) 7 12
n
v n n n n
suy ra
2
7 1.
n
u n n
0.25
Vậy
2
22
2021 2021( 7 1) 2021
lim lim .
25 4 2022 25 4 2022 2022
n
u n n
n n n n


0.25
4
Cho hình chóp
.S ABCD
có đáy
ABCD
là mt hình chữ nhật,
SA
vuông góc với mặt phẳng
ABCD
và
,,SA a AB b AD c
. Gọi
H
là hình chiếu vuông góc của
A
lên mặt phẳng
SBD
.
4a
Trong trường hợp
7, 1SA AB AD
, gọi
P
là mặt phẳng đi
qua
A
và vuông góc với
SC
. Hãy xác định thiết diện của hình
chóp
.S ABCD
khi cắt bởi mặt phẳng
P
và tính diện tích thiết
diện đó.
4
Gọi
'C
là hình chiếu vuông góc của
A
lên
SC
suy ra
' ( )CP
.
Có
,BD AC BD SA
BD SC
.
Mặt khác
( ) / /( )SC P BD P
.
Gọi
O AC BD
và
'I SO AC
. Trong
SBD
kẻ đường thẳng
qua
I
song song với
BD
, đường thẳng này cắt
,SB SD
lần lượt tại
', 'BD
. Khi đó thiết diện cần tìm là tứ giác
' ' 'AB C D
.
0.25
Ta có
()BD SAC
nên
'BD AC
mà
' '/ /B D BD
suy ra
' ' 'B D AC
. Lúc đó
' ' '
1
'. ' '
2
AB C D
S AC B D
.
0.25
Ta chứng minh được
'AD
là đường cao trong tam giác vuông
SAD
nên:
2
2
'. '
SA
SD SD SA SD
SD
.
Mặt khác
2
2
' ' ' '. . 7 2
''
8
B D SD SD BD SA BD
BD
BD SD SD SD
.
0.25
Vì
'AC
là đường cao trong tam giác vuông
SAC
nên
2 2 2
1 1 1 14
'
'3
AC
AC SA AC
.
Vậy:
' ' '
1 1 14 7 2 7 7
'. ' ' . . .
2 2 3 8 24
AB C D
S AC B D
0.25
4b
5
Chứng minh rằng
H
là trực tâm tam giác
SBD
.
Theo giả thiết
()AH SBD
, mặt khác
()SA ABD
nên
SA BD
suy ra
SH BD
(định lý ba đường vuông góc) tức là
H
thuộc một
đường cao của tam giác
SBD
.
0.5
Tương tự, ta cũng có
H
thuộc đường cao thứ hai của tam giác
SBD
.
Vậy
H
là trực tâm của tam giác
SBD
.
0.5
4c
Chứng minh rằng
3
. . .
2
HBD HSD HSB
abc
a S b S c S
, ở đây kí hiệu
XYZ
S
là diện tích của tam giác
XYZ
.
Gọi
'A SH BD
.
Vì
( ')BD SAA
nên
, ' 'ABD SBD SA A AA H
.
Lại do
AH SBD
nên
HBD
là hình chiếu vuông góc của
ABD
lên
SBD
.
Theo công thức định lý hình chiếu ta có:
cos ' sin
HBD
ABD
S AH
AA H ASH
S AS
.
0.25
Tương tự
,
HSD HSB
ASD ASB
S AH S AH
S AB S AD

.
Suy ra:
. . .
2
HBD HSD HSB
abc AH AH AH
a S b S c S
AS AB AD



.
0.25
Ta chứng minh được
2 2 2 2
1 1 1 1
AH AS AB AD
.
Nên
2
222
2 2 2
33
AH AH AH AH AH AH
AS AB AD AS AB AD






.
Suy ra:
3
AH AH AH
AS AB AD
.
0.25
Vậy
3
. . .
2
HBD HSD HSB
abc
a S b S c S
.
Đẳng thức xảy ra khi và chỉ khi
abc
.
0.25
6
5
Gọi
S
là tập hợp tất cả các số nguyên dương nhỏ hơn 1000. Mt
số thuc
S
được gọi là số “thú vị” nếu số đó là hợp số và không
chia hết cho ba số
2; 3; 5
. Chọn ngẫu nhiên mt số từ
S
, tính xác
suất đ số được chọn là số “thú vị”.
+) Gọi
,,A B C
lần lượt là các tập hợp các số thuộc S và chia hết cho
2;3;5.
Giả sử
xA
suy ra
*
2 , x k k
và
1 2 999 0.5 499.5 1;2;...;499k k k
. Suy ra số phần tử
của A là
499.A
Lập luận tương tự ta cũng có:
333,B
199C
.
+)
AB
là tập hợp các số thuộc S và chia hết cho 6 suy ra
166AB
,
AC
là tập hợp các số thuộc S và chia hết cho 10
suy ra
99AC
,
BC
là tập hợp các số thuộc S và chia hết cho
15 suy ra
66BC
.
+)
A B C
là tập hợp các số thuộc S và chia hết cho 30 suy
ra
33A B C
.
0.25
Dễ thấy tập hợp các số thuộc S chia hết cho ít nhất một trong ba số
2;3;5 là
A B C
và
499 333 199 166 99 66 33 733.
A B C A B C A B B C C A A B C
0.25
Do đó số các số tự nhiên nhỏ hơn 1000 và không chia hết cho cả ba
số 2;3;5 là 999 -733=266.
Trong tập hợp 266 số trên có cả số 1 và các số nguyên tố khác 2;3;5 .
Ta biết rằng có tất cả 165 số nguyên tố nhỏ hơn 1000 và khác 2;3;5.
Nên số các số ”thú vị” phải tìm là
266 165 1 100
số.
0.25
Số phần tử không gian mẫu là
999
.
Vậy xác suất cần tìm là
100
999
P
.
0.25
-------- HẾT --------
SỞ GD&ĐT QUẢNG BÌNH
ĐỀ CHÍNH THỨC
KỲ THI CHỌN HSG LỚP 11 NĂM HỌC 2021-2022
VÀ CHỌN ĐỘI DỰ TUYỂN DỰ THI CHỌN HSG
QUỐC GIA NĂM HỌC 2022-2023
Khóa ngày 25 tháng 4 năm 2022
Môn thi: TOÁN
SỐ BÁO DANH:……………
VÒNG 2
Thời gian: 180 phút (không kể thời gian giao đề)
Đề gồm có 01 trang và 04 câu.
Câu 1 (3,0 điểm).
a. Cho
,,x y z
là các số thực dương thỏa mãn điều kiện
1xyz
. Tìm giá trị nhỏ nhất của
biểu thức
3 3 3
222
.
( ) ( ) ( )
P
x y z y z x z x y
b. Tìm tất cả các cặp số nguyên dương
, , 1a b b
để hai số
3
1
1
ab
a
và
3
1
1
ba
b
đều là
số nguyên dương.
Câu 2 (2,0 điểm).
Cho dãy số
n
u
xác định bởi:
1
5
2
u
và
3
1
2022 2023
12 2002
1
n n n
n
u u u
n
với mọi
1n
.
a. Chứng minh rằng
2,
n
un
.
b. Chứng minh rằng dãy số
n
u
có giới hạn hữu hạn và tìm giới hạn đó.
Câu 3 (3,0 điểm). Cho tam giác nhọn
( )ABC AB AC
nội tiếp đường tròn
O
. Gọi
,GH
lần lượt là trọng tâm, trực tâm của tam giác
ABC
,
D
là chân đường cao của tam
giác
ABC
kẻ từ
A
,
M
là trung điểm của cạnh
BC
. Đường thẳng
DG
cắt cung nhỏ
BC
của
O
tại điểm
E
.
a. Chứng minh rằng
AB
là tiếp tuyến của đường tròn ngoại tiếp tam giác
BDE
.
b. Đường trung trực của cạnh
BC
cắt các đường thẳng
,AB AC
lần lượt tại
,PQ
. Gọi
N
là trung điểm của đoạn
PQ
. Chứng minh rằng đường thẳng
HM
cắt đường thẳng
AN
tại một điểm nằm trên đường tròn
O
.
Câu 4 (2,0 điểm). Người ta tô màu tất cả các số nguyên dương bằng hai màu xanh và đỏ
(mỗi số chỉ được tô đúng một màu). Biết rằng có vô hạn các số được tô màu xanh và tổng
của hai số được tô khác màu là một số được tô màu đỏ. Gọi số nguyên dương nhỏ nhất lớn
hơn 1 được tô màu đỏ là
q
.
a. Hãy chỉ ra (có chứng minh) một cách tô màu thỏa mãn yêu cầu bài toán khi
2q
.
b. Chứng minh rằng
q
là một số nguyên tố.
-------------hÕt-------------
1
SỞ GD&ĐT QUẢNG BÌNH
HƯỚNG DẪN CHẤM
KỲ THI CHỌN HSG LỚP 11 NĂM HỌC 2021-2022
VÀ CHỌN ĐỘI DỰ TUYỂN DỰ THI CHỌN HSG
QUỐC GIA NĂM HỌC 2022-2023
Khóa ngày 25 tháng 4 năm 2022
Môn thi: TOÁN
VÒNG 2
Đp n này gồm có 05 trang
YÊU CẦU CHUNG
* Đp n chỉ trình bày một lời giải cho mỗi câu. Trong bài làm của học sinh yêu cầu
phải lập luận lôgic chặt chẽ, đầy đủ, chi tiết và rõ ràng.
* Trong mỗi câu, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với những
bước giải sau có liên quan. Ở câu 3 nếu học sinh không vẽ hình hoặc vẽ hình sai thì cho
điểm 0.
* Điểm thành phần của mỗi câu nói chung phân chia đến 0,25 điểm. Đối với điểm
thành phần là 0,5 điểm thì tuỳ tổ gim khảo thống nhất để chiết thành từng 0,25 điểm.
* Học sinh có lời giải khc đp n (nếu đúng) vẫn cho điểm tối đa tuỳ theo mức điểm
của từng câu.
* Điểm của toàn bài là tổng (không làm tròn số) của điểm tất cả cc câu.
Câu
Ni dung
Đim
Câu 1a
Cho
,,x y z
là các số thực dương thỏa mãn điều kiện
1xyz
. Tìm giá trị
nhỏ nhất của biu thức
3 3 3
222
( ) ( ) ( )
P
x y z y z x z x y
.
Đặt
1 1 1
, , , , 0; 1a b c a b c abc
x y z
3 3 3 2 2 2
2 2 2
2
a bc b ac c ab a b c
P
b c a c a b b c c a a b



0.5
Áp dụng BĐT Cô-si ta được:
2
4
a b c
a
bc

,
2
4
b c a
b
ca

,
2
4
c a b
c
ab

.
0.5
Cộng từng vế ba BĐT trên ta có:
3
( ) 3 3P a b c abc
.
Dấu “=” xảy ra khi và chỉ khi
1abc
.
Vậy giá trị nhỏ nhất của
P
là
3
khi
1x y z
.
0.5
1b
Tìm tất cả các cặp số nguyên dương
, , 1a b b
đ hai số
3
1
1
ab
a
và
3
1
1
ba
b
đều là số nguyên dương.
Do
33
1 ( 1) ( 1)a b b a b
và
3
( 1) ( 1)aa
nên
( 1) ( 1)ab
(1)
Do
33
1 ( 1) ( 1)b a a b a
và
3
( 1) ( 1)bb
nên
( 1) ( 1)ba
(2)
0.5
Từ (1) và (2)
( 1) ( 1) ( 1) 2b b b
suy ra
2;3b
.
0.5
+) Nếu
2b
thì
( 1) 3a
suy ra
2a
. Nên
, 2,2ab
.
+) Nếu
3b
thì
( 1) 4a
suy ra
1, 3aa
. Nên
, 1,3ab
và
, 3,3ab
. Vậy có ba cặp số cần tìm là
1;3 ,(2;2), 3;3
.
0.5
2
2
Cho dãy số
n
u
xác định bởi:
1
5
2
u
và
3
1
2022 2023
12 2002
1
n n n
n
u u u
n
với mọi
1n
.
2a
Chứng minh rằng
2,
n
un
.
Viết lại
3
1
1
12 20
1
n n n
u u u
n
(1)
Ta chứng minh
2, 1
n
un
bằng phương pháp quy nạp:
Thật vậy
1
5
2
2
u 
, giả sử
2
n
u
.
Khi đó
3
1
1
2 12 16 0
1
n n n
u u u
n
2
1
4 2 0
1
nn
uu
n
(luôn đúng).
Chứng tỏ
2,
n
un
.
0.75
2b
Chứng minh rằng dãy số
n
u
có giới hạn hữu hạn và tìm giới
hạn đó.
Ta chứng minh
n
u
là dãy giảm
Ta có
21
72
4
uu
.
Giả sử
1
5
2 ...
2
n
uu
ta sẽ chứng minh
1nn
uu
, thật vậy:
22
11
33
11
22
1 1 1
11
12 0
1
11
. . 12 0(2)
1
n n n n
n n n n
n n n n n n
u u u u
u u u u
nn
u u u u u u
nn


Vì
1nn
uu
nên
1
0
nn
uu

và
2
n
u
,
1
2
n
u
suy ra
22
11
. 12 0
n n n n
u u u u

và
11
0
1nn

Do đó BĐT (2) đúng. Chứng tỏ
1
,
nn
u u n
.
0.5
Như vậy, dãy số
n
u
giảm và bị chặn dưới bởi 2 nên tồn tại
5
lim , 2
2
n
u L L



.
0.25
Lấy giới hạn ở đẳng thức truy hồi (1) ta có phương trình:
32
12 20 2 10 0L L L L L L
, ta có các nghiệm
1 2 3
1 41 5 1 41
2; ; 2
2 2 2
L L L
.
Vậy
lim 2
n
u
.
0.5
3
3
Cho tam giác nhọn
,( )ABC AB AC
ni tiếp đường tròn
O
. Gọi
,GH
lần lượt là trọng tâm, trực tâm của tam giác
ABC
,
D
là chân đường
cao của tam giác
ABC
kẻ từ
A
,
M
là trung đim của cạnh
BC
.
Đường thẳng
DG
cắt cung nhỏ
BC
của
O
tại đim
E
.
3a
Chứng minh rằng
AB
là tiếp tuyến của đường tròn ngoại tiếp
tam giác
BDE
.
Từ
A
kẻ đường thẳng song song với
BC
cắt
O
tại
,( )F F A
.
Ta chứng minh ba điểm
,,D G F
thẳng hàng, thật vậy:
Vì tứ giác
ABCF
là một hình thang nội tiếp
O
nên hình thang
ABCF
cân.
0.5
Gọi
T
là hình chiếu vuông góc của
F
lên
BC
BD TC
hay
M
là
trung điểm của
DT
.
0.25
Khi đó
1
2
DM GM
FA GA

kết hợp với
GMD GAF
suy ra
GMD
đồng
dạng với
G AF
. Lúc đó ta có
DGM FGA
.
Hay ba điểm
,,D G F
thẳng hàng.
0.5
Vì thế
BED BEF BCF ABC ABD
Suy ra
AB
là tiếp tuyến của đường tròn ngoại tiếp tam giác
BDE
.
0.25
4
3b
Đường trung trực của cạnh
BC
cắt các đường thẳng
,AB AC
lần
lượt tại
,PQ
. Gọi
N
là trung đim của đoạn
PQ
. Chứng minh
rằng đường thẳng
HM
cắt đường thẳng
AN
tại mt đim nằm
trên đường tròn
O
.
Có:
00
90 90 (1)APQ BPM MBP CBA HCB
và
00
90 90 (2)AQP MQC QCM ACB CBH
Từ (1) và (2) suy ra hai tam giác
,APQ HCB
đồng dạng.
0.5
Mà
,MN
lần lượt là trung điểm của
,BC PQ
Suy ra hai tam giác
,AQN HBM
cũng đồng dạng, vì thế ta có:
ANQ HMB
.
0.25
Gọi
L AN HM
, ta có:
0 0 0
180 180 90MLN LNM LMN LMB LMN
0.25
Kẻ đường kính
'AA
dễ dàng chứng minh được tứ giác
'BHCA
là hình
bình hành. Suy ra
,'HA
đối xứng nhau qua
M
suy ra
'A MH
.
Và
0
' 90A LA MLN
kết hợp
'AA
là đường kính nên ta có
()LO
.
0.5
4
Người ta tô màu tất cả các số nguyên dương bằng hai màu xanh
và đỏ (mỗi số chỉ được tô đúng mt màu). Biết rằng có vô hạn các
số được tô màu xanh và tổng của hai số được tô khác màu là mt
số được tô màu đỏ. Gọi số nguyên dương nhỏ nhất lớn hơn 1
được tô màu đỏ là
q
.
4a
Hãy chỉ ra (có chứng minh) mt cách tô màu thỏa mãn yêu cầu
bài toán khi
2q
.
Với
2q
ta chỉ ra một cách tô thỏa mãn yêu cầu bài toán như sau:
các số chia hết cho 3 ta tô màu xanh và các số không chia hết cho 3 ta
tô màu đỏ.
Cách tô như trên thỏa mãn yêu cầu bài toán, thật vậy:
+) Xét hai số nguyên dương
,yz
bất kỳ được tô bởi hai màu khác
nhau. Chứng tỏ trong hai số này có một số chia hết cho 3 và một số
không chia hết cho 3. Khi đó số
x y z
là một số không chia hết
cho 3 và sẽ được tô màu đỏ.
+) Có vô hạn số nguyên dương chia hết cho 3 nên có vô hạn số được
tô màu xanh.
+) Số nguyên dương nhỏ nhất lớn hơn 1 được tô màu đỏ là
2q
.
Như vậy khi
2q
ta xây dựng được một cách tô màu phù hợp với
yêu cầu bài toán.
0.5
5
4b
Chứng minh rằng
q
là mt số nguyên tố.
Với
3q
ta chỉ ra một cách tô thỏa mãn yêu cầu bài toán như sau:
Các số lẻ ta tô màu đỏ, các số chẵn ta tô màu xanh, lúc đó thỏa mãn
yêu cầu bài toán, thật vậy:
+) Xét hai số nguyên dương
,bc
bất kỳ được tô bởi hai màu khác
nhau. Chứng tỏ trong hai số này có một số chẵn và một số lẻ. Khi đó
số
a b c
là một số lẻ nên phải tô màu đỏ.
+) Có vô hạn số chẵn nên có vô hạn số được tô màu xanh.
+) Số nguyên dương nhỏ nhất lớn hơn 1 được tô màu đỏ là
3q
.
Như vậy, khi
3q
ta xây dựng một được cách tô màu phù hợp với
yêu cầu bài toán.
0.5
Ta chứng minh số
1
phải được tô màu đỏ.
Thật vậy, giả sử số 1 được tô màu xanh:
Vì
q
được tô màu đỏ nên
1q
được tô màu đỏ. Số
2 ( 1) 1qq
nên số
2q
được tô màu đỏ. Cứ tiếp tục như vậy thì mọi số lớn hơn
q
đều được tô màu đỏ. Nên chỉ có một số hữu hạn số được tô màu
xanh. Điều này mâu thuẫn với giả thiết.
Chứng tỏ số 1 phải được tô màu đỏ.
0.5
+) Với
3q
ta chứng minh không thể thực hiện được yêu cầu của bài
toán.
Thật vậy, giả sử tồn tại được cách tô ứng với
3q
,
Khi đó
2q

,
2qq
và số
2q
được tô màu xanh.
Do
1 ( 2) 1qq
nên số
1q
được tô màu đỏ.
Nhưng
1qq
, do đó ta có mâu thuẫn với giả thiết
q
là số nhỏ nhất
được tô màu đỏ.
Vậy bài toán được chứng minh xong.
0.5
-------- HẾT -------
| 1/13
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT QUẢNG BÌNH KỲ THI CHỌN HSG LỚP 11 NĂM HỌC 2021-2022
VÀ CHỌN ĐỘI DỰ TUYỂN DỰ THI CHỌN HSG ĐỀ CHÍNH THỨC
QUỐC GIA NĂM HỌC 2022-2023
Khóa ngày 25 tháng 4 năm 2022 Môn thi: TOÁN VÒNG 1
SỐ BÁO DANH:……………
Thời gian: 180 phút (không kể thời gian giao đề)
Đề gồm có 01 trang và 05 câu
Câu 1 (2,0 điểm).   
a. Giải phương trình 2 2 2sin x
 2sin x  tan x   .  4 
b. Chứng minh rằng phương trình 2 2022 2 2 m x
 2x x m  0 luôn có ít nhất hai nghiệm
phân biệt với mọi tham số m.
Câu 2 (2,0 điểm).
a. Cho n là số nguyên dương thỏa mãn 1 2
1.C  2.C  ...  . n
n C 16n. Tìm hệ số của số n n n 2n 1    hạng chứa 2 7
x trong khai triển của nhị thức 2 x    , x  0.  x
b. Cho cấp số cộng u có các số hạng đều là số nguyên và công sai d là một số n
dương. Biết rằng u m  0 và u  17 . Tính u . 20 m 2022
Câu 3 (2,0 điểm). 3
1 2x  1 3x
a. Tính giới hạn lim . 2 x 0  x
b. Cho dãy số u xác định bởi: u  9 và n   3 u
n  5 u  22 với mọi n 1. n 1    n  1 n Tính giới hạn 2021 u lim n . 2 25  4n  2022n
Câu 4 (3,0 điểm). Cho hình chóp .
S ABCD có đáy ABCD là hình chữ nhật, SA vuông góc
với mặt phẳng  ABCD và SA  , a AB  ,
b AD c . Gọi H là hình chiếu vuông góc của A
lên mặt phẳng SBD .
a. Trong trường hợp SA  7, AB AD 1, gọi P là mặt phẳng đi qua A và vuông
góc với SC . Hãy xác định thiết diện của hình chóp .
S ABCD khi cắt bởi mặt phẳng P
và tính diện tích thiết diện đó.
b. Chứng minh rằng H là trực tâm của tam giác SBD . abc c. Chứng minh rằng 3 . a S  . b S  . c S
, ở đây kí hiệu S là diện tích HBD HSD HSB 2 XYZ của tam giác XYZ .
Câu 5 (1,0 điểm). Gọi S là tập hợp tất cả các số nguyên dương nhỏ hơn 1000. Một số
thuộc S được gọi là số “thú vị” nếu số đó là hợp số và không chia hết cho ba số 2; 3; 5 .
Chọn ngẫu nhiên một số từ S , tính xác suất để số được chọn là số “thú vị”.
-------------HẾT -------------
SỞ GD&ĐT QUẢNG BÌNH KỲ THI CHỌN HSG LỚP 11 NĂM HỌC 2021-2022
VÀ CHỌN ĐỘI DỰ TUYỂN DỰ THI CHỌN HSG HƯỚNG DẪN CHẤM
QUỐC GIA NĂM HỌC 2022-2023
Khóa ngày 25 tháng 4 năm 2022 Môn thi: TOÁN VÒNG 1
Đáp án này gồm có 06 trang YÊU CẦU CHUNG
* Đáp án chỉ trình bày một lời giải cho mỗi câu. Trong bài làm của học sinh yêu cầu
phải lập luận lôgic chặt chẽ, đầy đủ, chi tiết và rõ ràng.
* Trong mỗi câu, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với
những bước giải sau có liên quan. Ở câu 4 nếu học sinh không vẽ hình hoặc vẽ hình sai thì cho điểm 0.
* Điểm thành phần của mỗi câu nói chung phân chia đến 0,25 điểm. Đối với điểm
thành phần là 0,5 điểm thì tuỳ tổ giám khảo thống nhất để chiết thành từng 0,25 điểm.
* Học sinh có lời giải khác đáp án (nếu đúng) vẫn cho điểm tối đa tuỳ theo mức điểm của từng câu.
* Điểm của toàn bài là tổng (không làm tròn số) của điểm tất cả các câu. Câu Nội dung Điểm    1a Giải phương trình 2 2 2sin x
 2sin x  tan x   .  4   ĐK: x   k 2    2
pt  1  cos 2x
 2sin x  tan x   0.25  2  2
 1  sin 2x  2sin x  tan x 2 2
 cos x  2sin xcos x  2sin xcos x  sin x
 sin x  cos x  2sin x cos x sin x  cos x  0 0.25
 sin x  cos x1 sin 2x  0
sin x  cos x  0
 1sin2x 0 0.25 tan x  1   sin2x 1   x  
k TM   4   
x   k TM   0.25  4  
Vậy phương trình có nghiệm là x    k và x   k . 4 4 1
Chứng minh rằng phương trình 2 2022 2 2 m x
 2x x m  0 luôn có 1b
ít nhất hai nghiệm phân biệt với mọi tham số m. x  0 TH1: 
m  0 Phương trình trở thành 2
2x x  0  1  (đúng). 0.25 x   2
TH2: m  0 Xét hàm số 2 2022 2 2 f ( ) x m x
 2x x m liên tục trên 0.25
nên nó liên tục trên các đoạn  1  ;  0 ,0;  1 .
Lại có: f    f   2 1 3,
0  m , f   1 1. 0.25
Nên f   f   2 1 . 0  3
m  0, f   f   2 0 . 1  m   0, m   . Suy ra trên mỗi khoảng  1  ;0,0;  1 phương trình 2 2022 2 2 m x
 2x x m  0 luôn có ít nhất 1 nghiệm. 0.25
Vậy phương trình đã cho luôn có ít nhất hai nghiệm phân biệt với mọi m .
Cho n là số nguyên dương thỏa mãn 1 2
1.C  2.C  ...  . n
n C 16n. n n n
Tìm hệ số của số hạng chứa 7
x trong khai triển của nhị thức 2a 2n 1   2  2 x   
, x  0. x  Đặt 1 2
S 1.C  2.C  ...  . n n C . n n n
Sử dụng công thức k n k C C  
với k  0;1;...;n , ta viết lại tổng S như n n sau: 0 S nCn  1 Cn  2 1 1 2 C ... 1 n C         . n n n n 0.25
Suy ra S n 0 1 2 2
C C C  ... nC . n n n n n n 1 2S . n 2 S . n 2      . Nên  S 16n hay n 1 . n 2
16n n  5 . 0.25 2n 1  11 11 k        Lúc đó: 11 2 2 k k 2 2 2 x   x   C  2 x      11     x   x    x k 0 0.25 11 k k  C  2   22 3k x  . 11 k 0
Ta tìm k sao cho 22 3k  7  k  5.
Vậy hệ số cần tìm là: 0.25 C  2  5 5  14  784. 11
Cho cấp số cộng u có các số hạng đều là số nguyên và có công sai d n 2b
là một số dương. Biết rằng u m  0 và u  17 . Tính u . 20 m 2022
Từ giả thiết: m u u 19d và 17  u u  (m 1)d . 20 1 m 1 0.25 20d  17 3
m 17 19d  m   1 d m   20  d  1 d  . 0.25 1
Vì m và d  0 nên d 1 là ước số lớn hơn 1 của 3 hay d 1 3. 0.25
Ta được d  2,m 19 . Vậy u  4023. 2022 0.25 2 3
1  2x  1  3x 3a Tính giới hạn lim . 2 x 0  x Ta có 3
1  2x  1  3x
1  2x   x   1 x   3 1  1  3x 0.25 lim  lim  lim 2 2 2 x 0  x 0  x 0 x xx
1  2x   x  2 1 x  3 1  1 3x  lim  lim x0 2
x  1 2x x   x0 1   0.25 xx  2 1   x   1
1  3x  1 3x2 2 3 3   1  x  3  lim  lim
x0  1 2x x   x0 1   0.25 x  2 1   x   1
1  3x  1 3x2 3 3   1 3 1    . 2 3 2 0.25 3    Vậy 1 2x 1 3x 1 lim  . 2 x 0  x 2
Cho dãy số u xác định bởi: u  9 và n   3 u
n  5 u  22 n 1    n  1 n 3b với mọi 2021u
n 1. Tính giới hạn lim n 2 25  4n . 2022n Với * n
  , đặt v u 11, khi đó v  20 và n n 1 22  n   3 v
11  n  5 v 11 . 0.25 n 1     n  n   3 vn  5 v . n 1    n n  5
(n  5)(n  4)
(n  5)(n  4)  v v vv n 1  n n 1  n2 n  3
(n  3)(n  2)
(n  2)(n  1) 0.25
(n  5)(n  4)  
v  (n  5)(n  4). 1 5.4 Nên 2
v  (n  4)(n  3)  n  7n 12 2
suy ra u n  7n 1. 0.25 n n 2   Vậy 2021u 2021(n 7n 1) 2021 lim n  lim  . 0.25 2 2
25  4n  2022n
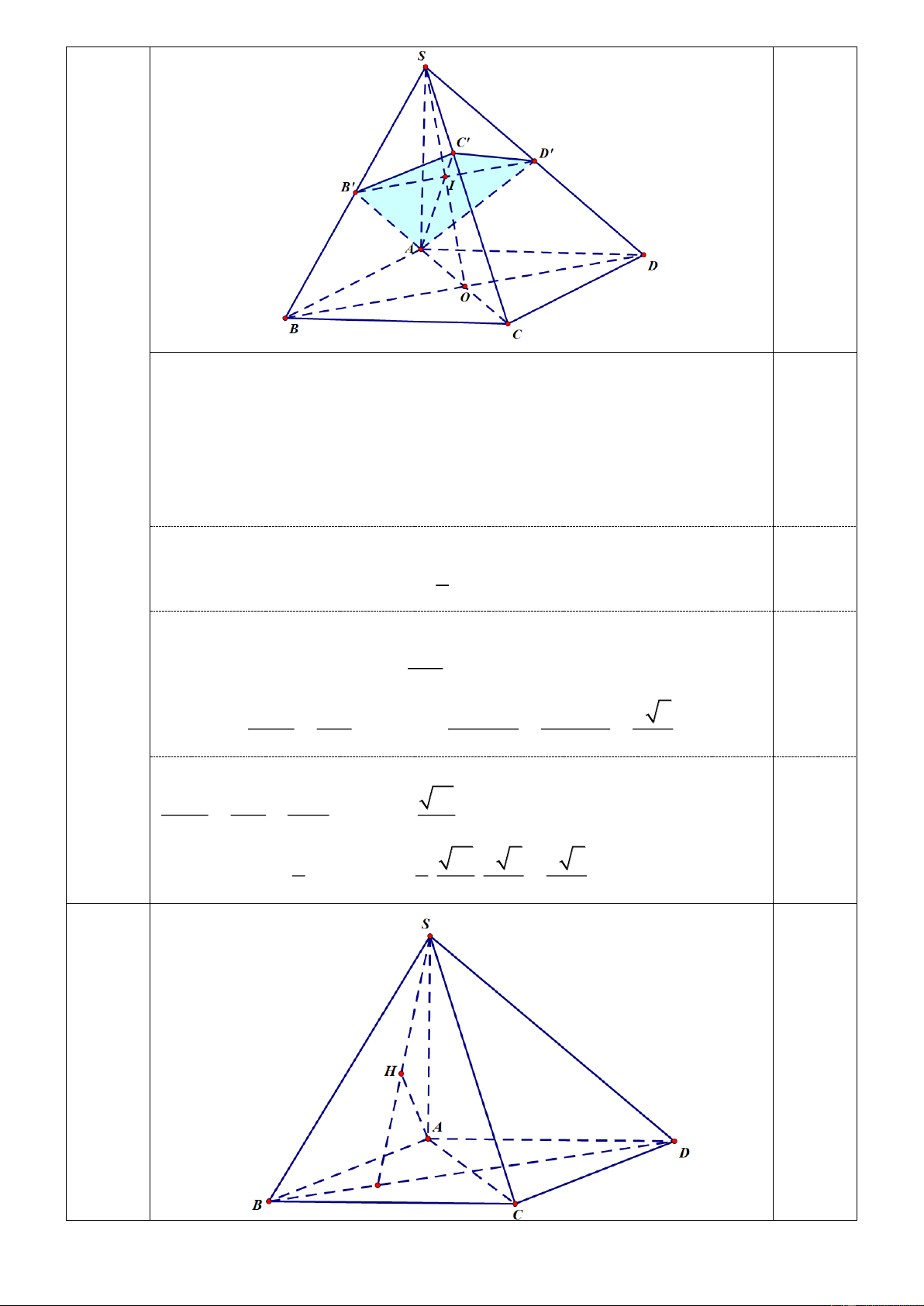
25  4n  2022n 2022 Cho hình chóp .
S ABCD có đáy ABCD là một hình chữ nhật, SA 4
vuông góc với mặt phẳng ABCD và SA  , a AB  ,
b AD c . Gọi
H là hình chiếu vuông góc của A lên mặt phẳng SBD.
Trong trường hợp SA  7, AB AD 1, gọi Plà mặt phẳng đi
qua A và vuông góc với SC . Hãy xác định thiết diện của hình 4a chóp .
S ABCD khi cắt bởi mặt phẳng P và tính diện tích thiết diện đó. 3
Gọi C ' là hình chiếu vuông góc của A lên SC suy ra C'( ) P .
Có BD AC, BD SA BD SC .
Mặt khác SC  (P)  BD / /(P) . Gọi 0.25
O AC BD và I SO AC '. Trong SBD kẻ đường thẳng
qua I song song với BD , đường thẳng này cắt S ,
B SD lần lượt tại
B ', D'. Khi đó thiết diện cần tìm là tứ giác AB'C ' D' .
Ta có BD  (SAC) nên BD AC' mà B'D'/ /BD suy ra 1 0.25
B'D'  AC' . Lúc đó S
AC '.B'D'.
AB 'C ' D ' 2
Ta chứng minh được AD ' là đường cao trong tam giác vuông SAD 2 nên: SA 2
SD'.SD SA SD '  . SD 0.25 2 Mặt khác B'D' SD ' SD '.BD SA .BD 7 2   B'D'    . 2 BD SD SD SD 8
Vì AC ' là đường cao trong tam giác vuông SAC nên 1 1 1 14    AC '  . 2 2 2 AC ' SA AC 3 0.25 Vậy: 1 1 14 7 2 7 7 S
AC '.B'D'  . .  .
AB 'C ' D ' 2 2 3 8 24 4b 4
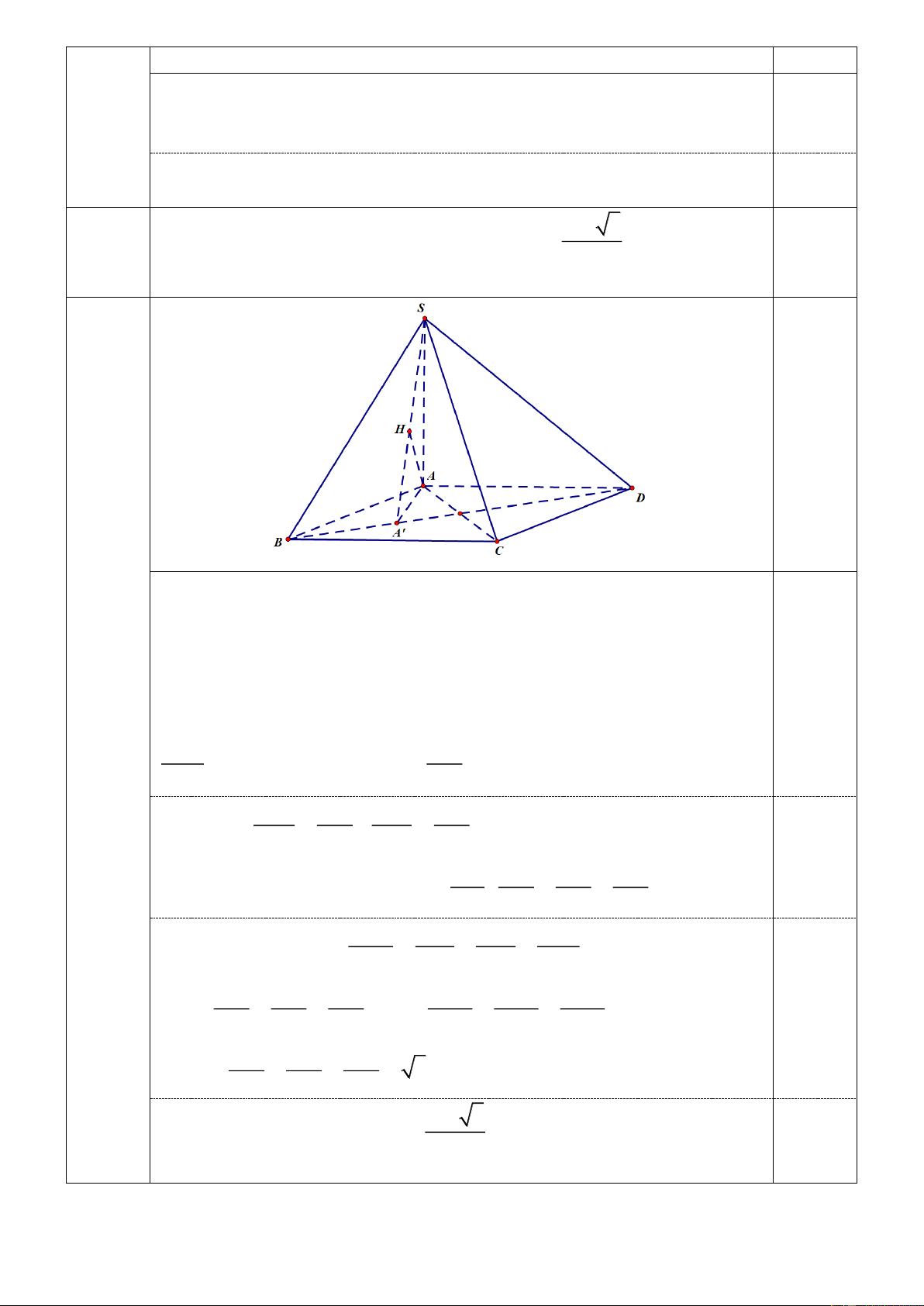
Chứng minh rằng H là trực tâm tam giác SBD .
Theo giả thiết AH  (SBD) , mặt khác SA  (ABD) nên SA BD
suy ra SH BD(định lý ba đường vuông góc) tức là H thuộc một 0.5
đường cao của tam giác SBD .
Tương tự, ta cũng có H thuộc đường cao thứ hai của tam giác SBD . Vậy 0.5
H là trực tâm của tam giác SBD . Chứng minh rằng abc 3 . a S  . b S  . c S, ở đây kí hiệu 4c HBD HSD HSB 2 S
là diện tích của tam giác XYZ . XYZ
Gọi A'  SH BD.
Vì BD  (SAA') nên  ABD,SBD  SA'A AA'H .
Lại do AH  SBD nên HBD là hình chiếu vuông góc của ABD lên SBD . 0.25
Theo công thức định lý hình chiếu ta có: S AH
HBD  cos AA' H  sin ASH  . S AS ABD Tương tự S AH S AH HSD  , HSB  . S AB S AD ASD ASB 0.25 abc AH AH AH  Suy ra: . a S  . b S  . c S    . HBD HSD HSB   2  AS AB AD  Ta chứng minh được 1 1 1 1    . 2 2 2 2 AH AS AB AD 2 2 2 2  AH AH AH   AH AH AH  Nên    3    3     . 0.25 2 2 2  AS AB AD   AS AB AD AH AH AH Suy ra:    3 . AS AB AD Vậy abc 3 . a S  . b S  . c S  . HBD HSD HSB 2 0.25
Đẳng thức xảy ra khi và chỉ khi a b c. 5
Gọi S là tập hợp tất cả các số nguyên dương nhỏ hơn 1000. Một
số thuộc S được gọi là số “thú vị” nếu số đó là hợp số và không 5 chia hết cho ba số
2; 3; 5 . Chọn ngẫu nhiên một số từ S , tính xác
suất để số được chọn là số “thú vị”. +) Gọi , A ,
B C lần lượt là các tập hợp các số thuộc S và chia hết cho 2;3;5. Giả sử x A suy ra *
x  2k, k  và
1 2k  999  0.5  k  499.5  k   1;2;...;49  9 . Suy ra số phần tử
của A là A  499.
Lập luận tương tự ta cũng có: B  333, C 199 . 0.25
+) A B là tập hợp các số thuộc S và chia hết cho 6 suy ra
A B 166, A C là tập hợp các số thuộc S và chia hết cho 10
suy ra A C  99 , B C là tập hợp các số thuộc S và chia hết cho
15 suy ra B C  66 .
+) AB C là tập hợp các số thuộc S và chia hết cho 30 suy
ra A B C  33.
Dễ thấy tập hợp các số thuộc S chia hết cho ít nhất một trong ba số
2;3;5 là AB C và
A B C A B C A B B C C A A B C 0.25
 499  333 199 166  99  66  33  733.
Do đó số các số tự nhiên nhỏ hơn 1000 và không chia hết cho cả ba số 2;3;5 là 999 -733=266.
Trong tập hợp 266 số trên có cả số 1 và các số nguyên tố khác 2;3;5 . 0.25
Ta biết rằng có tất cả 165 số nguyên tố nhỏ hơn 1000 và khác 2;3;5.
Nên số các số ”thú vị” phải tìm là 266  165   1 100 số.
Số phần tử không gian mẫu là   999 . 0.25
Vậy xác suất cần tìm là 100 P  . 999
-------- HẾT -------- 6
SỞ GD&ĐT QUẢNG BÌNH
KỲ THI CHỌN HSG LỚP 11 NĂM HỌC 2021-2022
VÀ CHỌN ĐỘI DỰ TUYỂN DỰ THI CHỌN HSG ĐỀ CHÍNH THỨC
QUỐC GIA NĂM HỌC 2022-2023
Khóa ngày 25 tháng 4 năm 2022 Môn thi: TOÁN VÒNG 2
SỐ BÁO DANH:……………
Thời gian: 180 phút (không kể thời gian giao đề)
Đề gồm có 01 trang và 04 câu.
Câu 1 (3,0 điểm). a. Cho , x ,
y z là các số thực dương thỏa mãn điều kiện xyz  1. Tìm giá trị nhỏ nhất của biểu thức 2 2 2 P    . 3 3 3
x ( y z)
y (z x)
z (x y) 3 a b 1 3 b a 1
b. Tìm tất cả các cặp số nguyên dương  ,
a b, b 1 để hai số và đều là a 1 b 1 số nguyên dương.
Câu 2 (2,0 điểm).
Cho dãy số u xác định bởi: n  5 2022n  2023 u  và 3 u
u 12u  2002  n  . 1  2 n 1 n n n  với mọi 1 1
a. Chứng minh rằng u 2, n     . n
b. Chứng minh rằng dãy số u có giới hạn hữu hạn và tìm giới hạn đó. n
Câu 3 (3,0 điểm). Cho tam giác nhọn ABC (AB AC) nội tiếp đường tròn O. Gọi ,
G H lần lượt là trọng tâm, trực tâm của tam giác ABC , D là chân đường cao của tam
giác ABC kẻ từ A , M là trung điểm của cạnh BC . Đường thẳng DG cắt cung nhỏ
BC của O tại điểm E .
a. Chứng minh rằng AB là tiếp tuyến của đường tròn ngoại tiếp tam giác BDE .
b. Đường trung trực của cạnh BC cắt các đường thẳng A ,
B AC lần lượt tại P,Q . Gọi
N là trung điểm của đoạn PQ . Chứng minh rằng đường thẳng HM cắt đường thẳng AN
tại một điểm nằm trên đường tròn O.
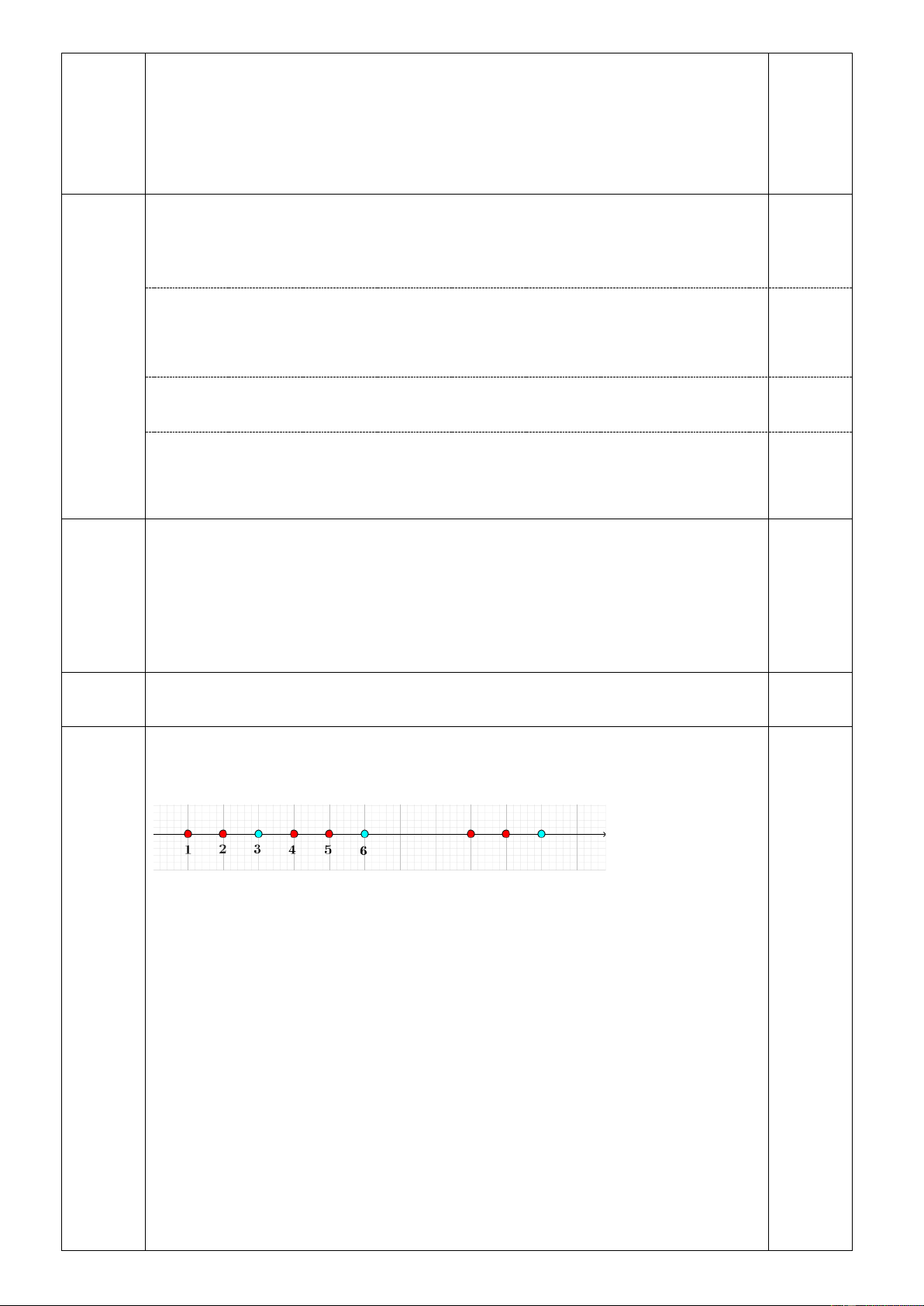
Câu 4 (2,0 điểm). Người ta tô màu tất cả các số nguyên dương bằng hai màu xanh và đỏ
(mỗi số chỉ được tô đúng một màu). Biết rằng có vô hạn các số được tô màu xanh và tổng
của hai số được tô khác màu là một số được tô màu đỏ. Gọi số nguyên dương nhỏ nhất lớn
hơn 1 được tô màu đỏ là q .
a. Hãy chỉ ra (có chứng minh) một cách tô màu thỏa mãn yêu cầu bài toán khi q  2 .
b. Chứng minh rằng q là một số nguyên tố.
-------------hÕt-------------
SỞ GD&ĐT QUẢNG BÌNH
KỲ THI CHỌN HSG LỚP 11 NĂM HỌC 2021-2022
VÀ CHỌN ĐỘI DỰ TUYỂN DỰ THI CHỌN HSG HƯỚNG DẪN CHẤM
QUỐC GIA NĂM HỌC 2022-2023
Khóa ngày 25 tháng 4 năm 2022 Môn thi: TOÁN VÒNG 2
Đáp án này gồm có 05 trang YÊU CẦU CHUNG
* Đáp án chỉ trình bày một lời giải cho mỗi câu. Trong bài làm của học sinh yêu cầu
phải lập luận lôgic chặt chẽ, đầy đủ, chi tiết và rõ ràng.
* Trong mỗi câu, nếu học sinh giải sai ở bước giải trước thì cho điểm 0 đối với những
bước giải sau có liên quan. Ở câu 3 nếu học sinh không vẽ hình hoặc vẽ hình sai thì cho điểm 0.
* Điểm thành phần của mỗi câu nói chung phân chia đến 0,25 điểm. Đối với điểm
thành phần là 0,5 điểm thì tuỳ tổ giám khảo thống nhất để chiết thành từng 0,25 điểm.
* Học sinh có lời giải khác đáp án (nếu đúng) vẫn cho điểm tối đa tuỳ theo mức điểm của từng câu.
* Điểm của toàn bài là tổng (không làm tròn số) của điểm tất cả các câu. Câu Nội dung Điểm Cho ,
x y, z là các số thực dương thỏa mãn điều kiện xyz 1. Tìm giá trị
Câu 1a nhỏ nhất của biểu thức 2 2 2 P    . 3 3 3
x ( y z)
y (z x)
z (x y) Đặt 1 1 1 a  ,b  ,c   a, ,
b c  0;abc 1 x y z 0.5 3 3 3 2 2 2 2a bc 2b ac 2c aba b cP     2     b c a c a b
b c c a a b
Áp dụng BĐT Cô-si ta được: 2 a b c 2  2    b c a c a b 0.5 a ,   b,   c. b c 4 c a 4 a b 4
Cộng từng vế ba BĐT trên ta có: 3
P  (a b c)  3 abc  3.
Dấu “=” xảy ra khi và chỉ khi a b c 1. 0.5
Vậy giá trị nhỏ nhất của P là 3 khi x y z 1. 3  Tìm a b 1
tất cả các cặp số nguyên dương  ,
a b, b 1 để hai số và a 1 1b 3
b a 1 đều là số nguyên dương. b 1 Do 3 3 a b 1  (
b a 1)  (b 1) và 3
(a  1) (a  1) nên (a 1) (b 1) (1) 0.5 Do 3 3
b a 1  a(b 1)  (a 1) và 3
(b 1) (b 1) nên (b 1) (a 1) (2)
Từ (1) và (2) (b 1) (b 1)  (b 1) 2 suy ra b2;  3 . 0.5
+) Nếu b  2 thì (a 1) 3 suy ra a  2. Nên  , a b  2,2 .
+) Nếu b  3 thì (a 1) 4 suy ra a 1, a  3 . Nên  , a b  1,  3 và 0.5  ,ab 3, 
3 . Vậy có ba cặp số cần tìm là 1;  3 ,(2;2),3;3 . 1
Cho dãy số u xác định bởi: n 2 5 2022n  2023 u và 3 u
u 12u  2002  n . 1  2 n 1 n n n với mọi 1 1 2a
Chứng minh rằng u 2, n     . n Viết lại 1 3 u
u 12u  20  n 1  n n n (1) 1
Ta chứng minh u  2, n
 1 bằng phương pháp quy nạp: n Thật vậy 5 u
 2 , giả sử u  2 . 1 2 n 0.75 Khi đó 1 3 u
 2  u 12u 16   0 n 1  n n n  1  u u    (luôn đúng). n  n 2 1 4 2 0 n  1 Chứng tỏ u 2, n     . n
Chứng minh rằng dãy số u có giới hạn hữu hạn và tìm giới n 2b hạn đó.
Ta chứng minh u là dãy giảm n  Ta có 7 2 u   u . 2 1 4 Giả sử 5
2  u  ...  u  ta sẽ chứng minh uu , thật vậy: n 1  2 n 1 n 2 2 u
u u u n 1  n n 1  n 1 1   3 3 u u 12 u u    0 0.5 n n 1  
n n 1 n1 n  u u u u uu     n n . 1 1 2 2 . 12 0(2) 1 n n n 1  n 1   n1 n
Vì u u nên u u  0 và n n 1  n n 1     u  2 , u 2 suy ra 2 2
u u .uu 12  0 và 1 1 0 n n 1  n n n 1  n 1  n  1 n
Do đó BĐT (2) đúng. Chứng tỏ u u , n    . n 1  n
Như vậy, dãy số u giảm và bị chặn dưới bởi 2 nên tồn tại n   5  0.25 limu  , L 2  L  . n    2 
Lấy giới hạn ở đẳng thức truy hồi (1) ta có phương trình: 3 L L L   L   2 12 20
2 L L 10  0, ta có các nghiệm 1   41 5 1   41 L  2; L   ;L   2 . 1 2 3 0.5 2 2 2 Vậy limu  2 . n 2
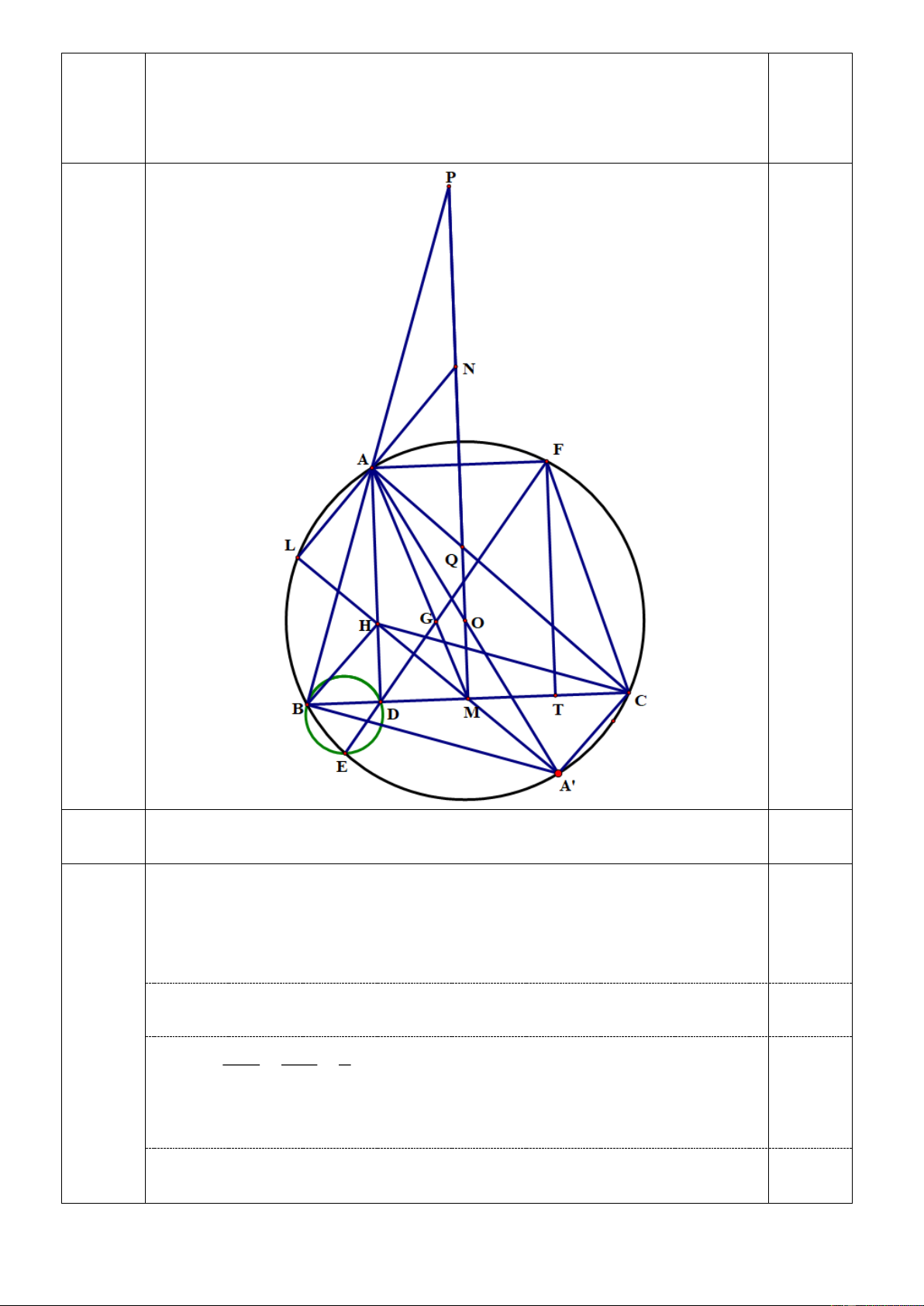
Cho tam giác nhọn ABC,(AB AC) nội tiếp đường tròn O. Gọi G, H
lần lượt là trọng tâm, trực tâm của tam giác ABC , D là chân đường 3 cao của tam giác
ABC kẻ từ A , M là trung điểm của cạnh BC .
Đường thẳng DG cắt cung nhỏ BC của O tại điểm E .
Chứng minh rằng AB là tiếp tuyến của đường tròn ngoại tiếp 3a tam giác BDE .
Từ A kẻ đường thẳng song song với BC cắt O tại F,(F  ) A . Ta chứng minh ba điểm , D ,
G F thẳng hàng, thật vậy: 0.5
Vì tứ giác ABCF là một hình thang nội tiếp O nên hình thang ABCF cân.
Gọi T là hình chiếu vuông góc của F lên BC BD TC hay M là trung điểm của 0.25 DT . DM GM 1 Khi đó 
 kết hợp với GMD GAF suy ra GMD đồng FA GA 2 dạng với  0.5
GAF . Lúc đó ta có DGM FGA . Hay ba điểm , D , G F thẳng hàng.
Vì thế BED BEF BCF ABC ABD 0.25
Suy ra AB là tiếp tuyến của đường tròn ngoại tiếp tam giác BDE . 3
Đường trung trực của cạnh BC cắt các đường thẳng A , B AC lần
lượt tại P,Q . Gọi N là trung điểm của đoạn PQ . Chứng minh 3b
rằng đường thẳng
HM cắt đường thẳng AN tại một điểm nằm
trên đường tròn O. Có: 0 0
APQ BPM  90  MBP  90  CBA HCB (1) và 0 0
AQP MQC  90  QCM  90  ACB CBH (2) 0.5
Từ (1) và (2) suy ra hai tam giác AP , Q HCB đồng dạng.
Mà M , N lần lượt là trung điểm của BC, PQ
Suy ra hai tam giác AQN, HBM cũng đồng dạng, vì thế ta có: 0.25 ANQ HMB .
Gọi L AN HM , ta có: 0.25 0 0 0
MLN  180  LNM LMN  180  LMB LMN  90
Kẻ đường kính AA' dễ dàng chứng minh được tứ giác BHCA' là hình
bình hành. Suy ra H, A'đối xứng nhau qua M suy ra A' MH . 0.5 Và 0
A' LA MLN  90 kết hợp AA' là đường kính nên ta có L ( ) O .
Người ta tô màu tất cả các số nguyên dương bằng hai màu xanh
và đỏ (mỗi số chỉ được tô đúng một màu). Biết rằng có vô hạn các 4
số được tô màu xanh và tổng của hai số được tô khác màu là một
số được tô màu đỏ. Gọi số nguyên dương nhỏ nhất lớn hơn 1
được tô màu đỏ là q .
Hãy chỉ ra (có chứng minh) một cách tô màu thỏa mãn yêu cầu 4a bài toán khi q  2 .
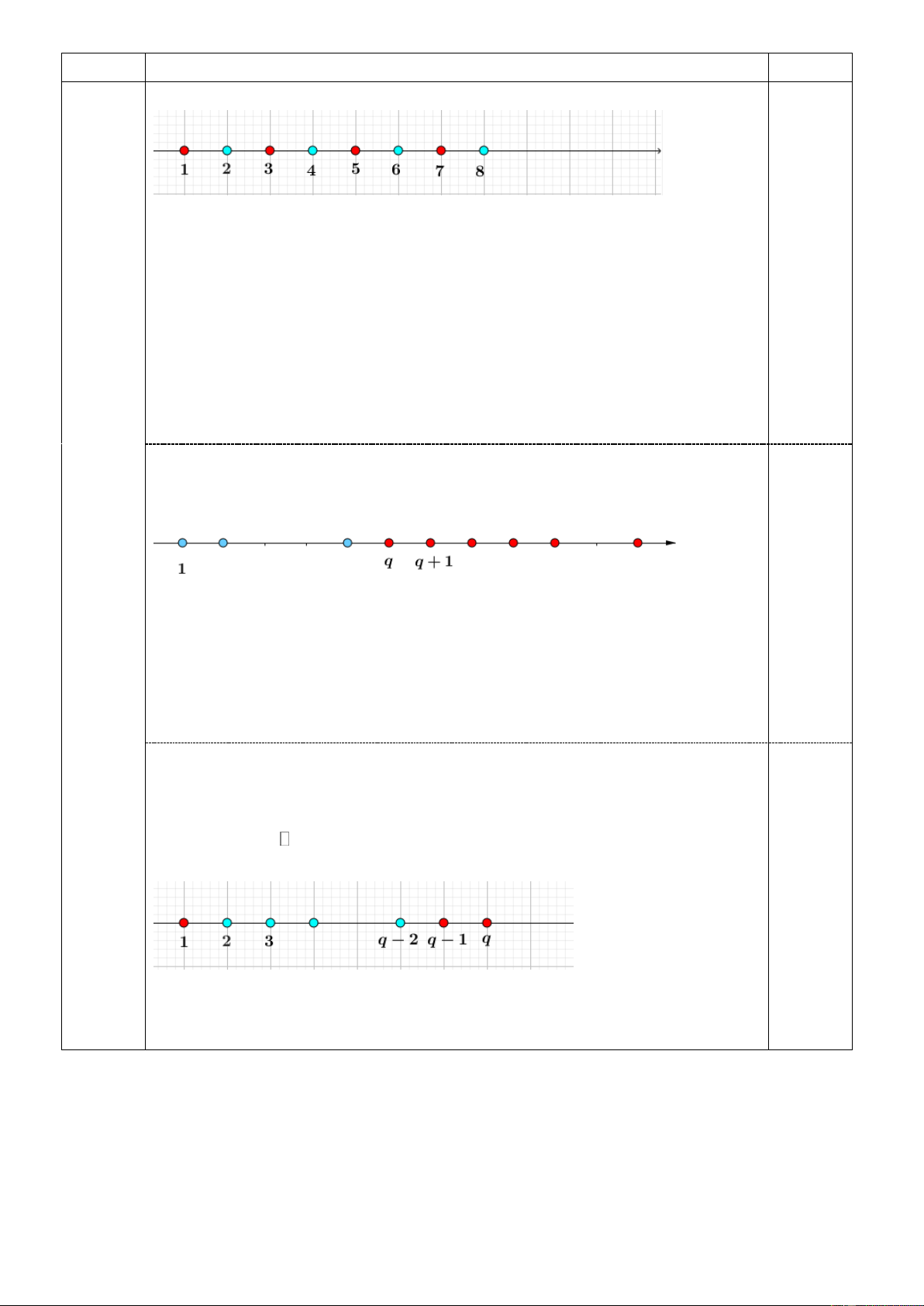
Với q  2 ta chỉ ra một cách tô thỏa mãn yêu cầu bài toán như sau:
các số chia hết cho 3 ta tô màu xanh và các số không chia hết cho 3 ta tô màu đỏ.
Cách tô như trên thỏa mãn yêu cầu bài toán, thật vậy:
+) Xét hai số nguyên dương ,
y z bất kỳ được tô bởi hai màu khác
nhau. Chứng tỏ trong hai số này có một số chia hết cho 3 và một số
không chia hết cho 3. Khi đó số x y z là một số không chia hết
cho 3 và sẽ được tô màu đỏ. 0.5
+) Có vô hạn số nguyên dương chia hết cho 3 nên có vô hạn số được tô màu xanh.
+) Số nguyên dương nhỏ nhất lớn hơn 1 được tô màu đỏ là q  2.
Như vậy khi q  2 ta xây dựng được một cách tô màu phù hợp với yêu cầu bài toán. 4 4b
Chứng minh rằng q là một số nguyên tố.
Với q  3 ta chỉ ra một cách tô thỏa mãn yêu cầu bài toán như sau:
Các số lẻ ta tô màu đỏ, các số chẵn ta tô màu xanh, lúc đó thỏa mãn
yêu cầu bài toán, thật vậy:
+) Xét hai số nguyên dương b,c bất kỳ được tô bởi hai màu khác
nhau. Chứng tỏ trong hai số này có một số chẵn và một số lẻ. Khi đó
số a b c là một số lẻ nên phải tô màu đỏ.
+) Có vô hạn số chẵn nên có vô hạn số được tô màu xanh.
+) Số nguyên dương nhỏ nhất lớn hơn 1 được tô màu đỏ là 0.5 q  3.
Như vậy, khi q  3 ta xây dựng một được cách tô màu phù hợp với yêu cầu bài toán.
Ta chứng minh số 1 phải được tô màu đỏ.
Thật vậy, giả sử số 1 được tô màu xanh: 0.5
Vì q được tô màu đỏ nên q 1 được tô màu đỏ. Số q  2  (q 1) 1
nên số q  2 được tô màu đỏ. Cứ tiếp tục như vậy thì mọi số lớn hơn
q đều được tô màu đỏ. Nên chỉ có một số hữu hạn số được tô màu
xanh. Điều này mâu thuẫn với giả thiết.
Chứng tỏ số 1 phải được tô màu đỏ.
+) Với q  3 ta chứng minh không thể thực hiện được yêu cầu của bài toán.
Thật vậy, giả sử tồn tại được cách tô ứng với q  3, Khi đó q 2   
, q  2  q và số q  2 được tô màu xanh.
Do q 1  (q  2) 1 nên số q 1được tô màu đỏ. 0.5
Nhưng q 1 q , do đó ta có mâu thuẫn với giả thiết q là số nhỏ nhất được tô màu đỏ.
Vậy bài toán được chứng minh xong. -------- HẾT ------- 5
Document Outline

  • 1__TOAN_11_VONG_1_2022_14126e258d
  • 2__TOaN_11_VONG_2_2022_8f060cc8d5