Đề thi chọn HSG Toán 11 năm 2023 – 2024 trường THPT Tiên Lãng – Hải Phòng

SỞ GD&ĐT HẢI PHÒNG
KỲ THI CHỌN HSG LỚP 11 THPT NĂM HỌC 2023-2024 TRƯỜNG THPT TIÊN LÃNG ĐỀ THI MÔN: TOÁN HỌC
Thời gian làm bài: 150 phút, không kể thời gian phát đề. ĐỀ CHÍNH THỨC Ngày thi: 20/04/2024
(Đề thi gồm 07 câu; 02 trang) Câu 1:(1,0 điểm) x  3 1 Cho hàm số y 
có đồ thị C . Chứng minh rằng đường thẳng d : y  x m luôn cắt x  2 2
đồ thị C  tại hai điểm ,
A B phân biệt. Tìm giá trị nhỏ nhất của độ dài đoạn thẳng AB . Câu 2:(2,0 điểm)
1. Cho các số thực dươnga, ,
b c lớn hơn 1, đặt x  log b  log , a y  log c  log b và a b b c
z  log a  log c . Tính giá trị của biểu thức 2 2 2 x  y  z  xyz . c a
2. Có bao nhiêu bộ x;y với x,y nguyên và 1  x,y  2023 thỏa mãn:         xy  x  y   2y 2x 1 2 4 8 log 
  2x  3y  xy  6 log      ? 3   2 y  2    x  3  Câu 3:(2,0 điểm) 1. Giải phương trình: 2
4 cos x 1  sinx 2 3 cosx cos2x  1  2sinx . 3 2 3 x
  3x  4x  2  y y 
2. Giải hệ phương trình : . 4
 x 6 x 1 7   4x  1y Câu 4:(2,0 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a , tam giác SAB vuông tại S
và nằm trong mặt phẳng vuông góc với mặt phẳng đáy
1. Chứng minh rằng: SA  SBC .
2. Biết góc giữa SD và mặt phẳng SAB bằng 0
60 . Tính khoảng cách từ điểm C đến SBD Câu 5:(1,0 điểm)
Trong một hộp kín đựng 2024 tấm thẻ như nhau được đánh số từ 1 đến 2024 . Lấy ngẫu nhiên
ba tấm thẻ trong hộp. Tính xác suất để lấy được ba tấm thẻ mà ba số ghi trên ba tấm thẻ đó lập
thành một cấp số cộng. Câu 6:(1,0 điểm).
Trong mặt phẳng với hệ trục toạ độ Oxy cho hình vuông ABCD tâm I . Gọi M,N,J lần lượt
là trung điểm các đoạn thẳng AI,C ,
D BN . Biết phương trình đường thẳng MJ là y 2 7  0 và N 5; 
6 . Biết đỉnh C có hoành độ lớn hơn 3 . Tìm tọa độ đỉnh C của hình vuông ABCD . 1 Câu 7:(1,0 điểm) Cho a, ,
b c là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức:
3b c 4a  3c 12b c T    . 2a 3b 2a  3c
-----------------------HẾT------------------------- 2 TRƯỜNG THPT TIÊN LÃNG
KỲ THI CHỌN HSG LỚP 11 THPT NĂM HỌC 2023-2024 TỔ TOÁN-VP ĐỀ THI MÔN: TOÁN HỌC
Thời gian làm bài: 150 phút, không kể thời gian phát đề. HD ĐỀ CHÍNH THỨC Ngày thi: 20/04/2024
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM MÔN TOÁN
(Hướng dẫn chấm có 06 trang) CÂU ĐÁP ÁN ĐIỂM x  3 1 Cho hàm số y 
có đồ thị C . Chứng minh rằng đường thẳng d : y  x m x  2 2 1,0
luôn cắt đồ thị C  tại hai điểm ,
A B phân biệt. Tìm giá trị nhỏ nhất của độ dài đoạn thẳng AB .
Phương trình hoành độ giao điểm của C  và d là x  3 1 2 x  2mx 4m 6  0  x m   x  2 2 x   2   0,25 2
 x  2mx  4m  6  0  1 (Vì x  2
 không là nghiệm của phương trình  1 với mọi m ).
Ta có   m  m   m  2 2 ' 4 6 2  2  0, m   . 1 Suy ra phương trình  
1 luôn có hai nghiệm phân biệt x ,x với mọim hay 0,25 1 2
đường thẳng d luôn cắt đồ thị C  tại hai điểm , A B phân biệt.  1   1  Gọi A x
 ; x m, B x ; x m. 1 1  2  2 2  2  2 2 1 1    5
Suy ra AB  x x  x m  x  m  x  x 0,25 2 1 2 1   2 1 2 2  2 5 2 '  .  5 2 m  4m  6 2 1  m  2 5
2  10  10, m   . 0,25
Đẳng thức xảy ra khi m  2  . Vậy minAB  10 .
Cho các số thực dươnga, ,
b c lớn hơn 1, đặt x  log b  log a,y  log c  log b và a b b c 1,0
z  log a  log c . Tính giá trị của biểu thức 2 2 2 x  y  z  xyz c a
Ta có: xyz  log b  log clog c  log alog a  log b c b a c b a  0,5   b  c  c  b  a  a  a 2
 a 2  b 2  c 2  c 2  b 2 log log log log log log 2 2.1 x  y  z   b  c2  c  a2  a  b2 2 2 2 log log log log log log c b a c b a 2 2 2 2 2 2
 log b  log c log c log b log a log a  6 0,5 a a b c c b Từ   1 và 2 suy ra: 2 2 2 x  y  z  xyz  4 . 1
Có bao nhiêu bộ x;y với x,y nguyên và 1  x,y  2023 thỏa mãn:  2y     2x  1 1,0
xy  2x  4y  8log 
  2x  3y  xy  6 log      ? 3   2 y  2    x  3  * x
 ,y   : x,y  2023 *  x
 ,y   : x,y  2023 Điều kiện 2x  1 2    . 0,25   0, y  0 x   3,y  0  x  3 y  2  BPT cho có dạng          x  y   x 4 y 2 3 2 log 
 1  x  4 y  2 log      1  0 (*). 0,25 2    3 x  3    y  2  x  4    2 TH1: Xét
thì (*) thành x  3log   1  3 x  4 log  0 , 2     y  1 3 x  3  3
rõ ràng BPT này nghiệm đúng với mọi x  3 vì x  4    2 0,25
x  3  0, log 
 1  log 0  1  0, 3 x  4  0, log  0 2   2     3 x  3  3 2.2
Như vậy trường hợp này cho ta đúng 2020 bộ x;y  x;  1 với 4  x  2023,x   .
TH2: Xét y  2 thì (*) thành 4x  4log 1  0 , BPT này cũng luôn đúng với 3
mọi x mà 4  x  2023,x   .
Trường hợp này cho ta 2020 cặp x;y nữa. 0,25
TH3: Xét y  2,x  3 thì VT  
*  0 nên (*) không xảy ra.
Vậy có đúng 4040 bộ số x;y thỏa mãn yêu cầu bài toán. Giải phương trình: 2
4 cos x 1 sinx 2 3 cosx cos2x  1 2sinx 1,0
Phương trình tương đương với: ` 2 2
4cos x  4cos x. sinx  2 3 cosx cos2x  1  2sinx . 2 2
 2sinx(2cos x 1)  2 3 cosx cos2x  4cos x 1  0 . 2 2
 2sinx cos2x  2 3 cosx cos2x  3cos x  sin x  0 . 3.1
 2 cos2x sinx  3 cosx 3 cosx  sinx 3 cosx sinx  0. 0,5
  3 cosx  sinx2cos2x  3 cosx sinx  0.  3cosx  sinx  0  
2cos2x  3 cosx  sinx  0  
+) 3 cosx  sin x  0  tanx   3  x    kk  . 0,25 3 2  5 
+) 2 cos2x  3 cosx  sin x  0  cos2x  cos x        6   5 x     k2   6  k  .  5 k2 x    0,25  18 3 
Vậy phương trình có nghiệm: x    k , 3 5 5 k2 x    2k , x     k  . 6 18 3  3 2 3 x
  3x  4x  2  y y   1
Giải hệ phương trình : . 4
 x  6 x 1  7  1,0  4x  1y  2 3
Phương trình    x    x   3 1 1 1  y  y x y x 2 x  2 1 1 1 y y 1           0     y  x  1 0,5 2 2 2  y  y
(vì x   x   2 3 1 1 y  y  1  x   1     1  0 x,y  ).  2 4 3.2 Thay y  x  1 vào phương trình 2, ta được: 0,25
4x  6 x 1  7  4x  1x  1 x   1  x   1         x 1  3  2 2  4x  x 1  3  2x   3 x   0,25    2  x  2  y  3 . x  1   2x 32
Vậy hệ phương trình có nghiệm: x;y  2;3.
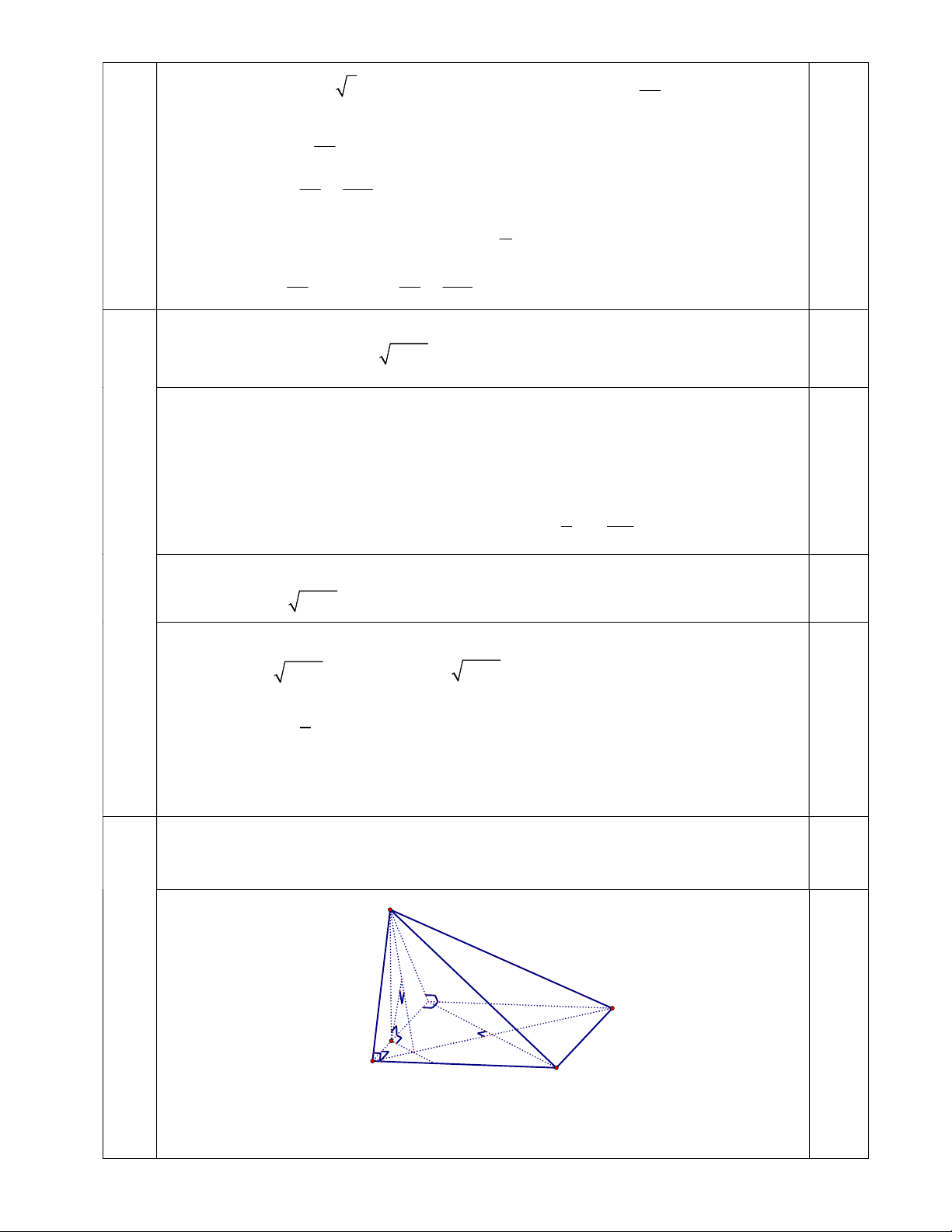
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 3a , tam giác SAB vuông tại
S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. 1,0
1. Chứng minh rằng: SA  SBC . S I 4.1 A 3a D 0,5 H K O B C
Gọi H  AB : SH  AB  SH  ABCD  SH  BC , mà BC  AB
nên BC  SAB  BC  SA 3 S  A  SB Ta lại có:   SA  SBC S  A  BC (đpcm). 0,5 
Biết góc giữa SD và mặt phẳng SAB bằng 0
60 . Tính khoảng cách từ điểm C đến  1,0 SBD.
Theo 1) ta có BC  SAB. A  D//BC Do   
, do đó hình chiếu vuông góc của SD lên B  C  0,25  SAB AD SAB SAB là SA hay  ASD  60.
Kẻ HK  BD và HI  SK , khi đó B  D  HK  H  I  SK   BD  HI  B  D  SH và   HI  SBD .  H  I  BD  0,25  d H,SBD  HI AD
Xét tam giác vuông SAD ta có: SA   a 3 và tanASD 4.2 AD SD    2a 3 . sinASD Và 2 2 2 2
SB  AB  SA  9a  3a  a 6 . Ta tính 2 2 SA .SB SH   2a và 2 2 2 2
BH  SB  SH  6a  2a  2a . 0,25 2 2 SA  SB Vì vậy ta có tỉ lệ HK HB 2 2 3 2     . a HK  2a . AO AB 3 3 2 2 2 SH .HK Khi đó HI   a . 2 2 SH  HK d H,SBD HB 2 Ta có   d  ,ASBD AB 3 0,25 3 3 3a
Vậy d C,SBD  d ,
A SBD  dH,SBD  HI  2 2 2
Trong một hộp kín đựng 2024 tấm thẻ như nhau được đánh số từ 1 đến 2024. Lấy ngẫu
nhiên ba tấm thẻ trong hộp. Tính xác suất để lấy được ba tấm thẻ mà ba số ghi trên ba tấm 1,0
thẻ đó lập thành một cấp số cộng.
Số phần tử của không gian mẫu: 3 n( )   C . 2024 0,25 5
Biến cố A : “lấy được ba tấm thẻ mà ba số ghi trên ba tấm thẻ đó lập thành một cấp số cộng”.
Gọi ba số lập thành cấp số cộng lần lượt là: u , u , u . 0,25 1 2 3
Khi đó u , u phải cùng là hai số chẵn hoặc cùng là hai số lẻ. 1 3
Từ 1 đến 2024 có 1012 số chẵn, 1012 số lẻ. 0,25 4
+ Trường hợp 1: u , u là hai số chẵn, có 2
C cách chọn bộ u ; u . 1 3  1 3 1012
+ Trường hợp 2: u , u là hai số lẻ, có 2
C cách chọn bộ u ; u . 1 3  1 3 1012
Với mỗi cách chọn bộ u ; u có duy nhất một cách chọn u để u , u , u lập 1 3  2 1 2 3 thành cấp số cộng.
Suy ra số cách lấy được 3 thẻ ghi ba số lập thành cấp số cộng là 2 n( ) A  2C . 1012
Xác suất lấy được 3 thẻ ghi ba số lập thành cấp số cộng là P   2 n( ) A 2C1012 3 A    . 0,25 3 n( )  C 4046 2024
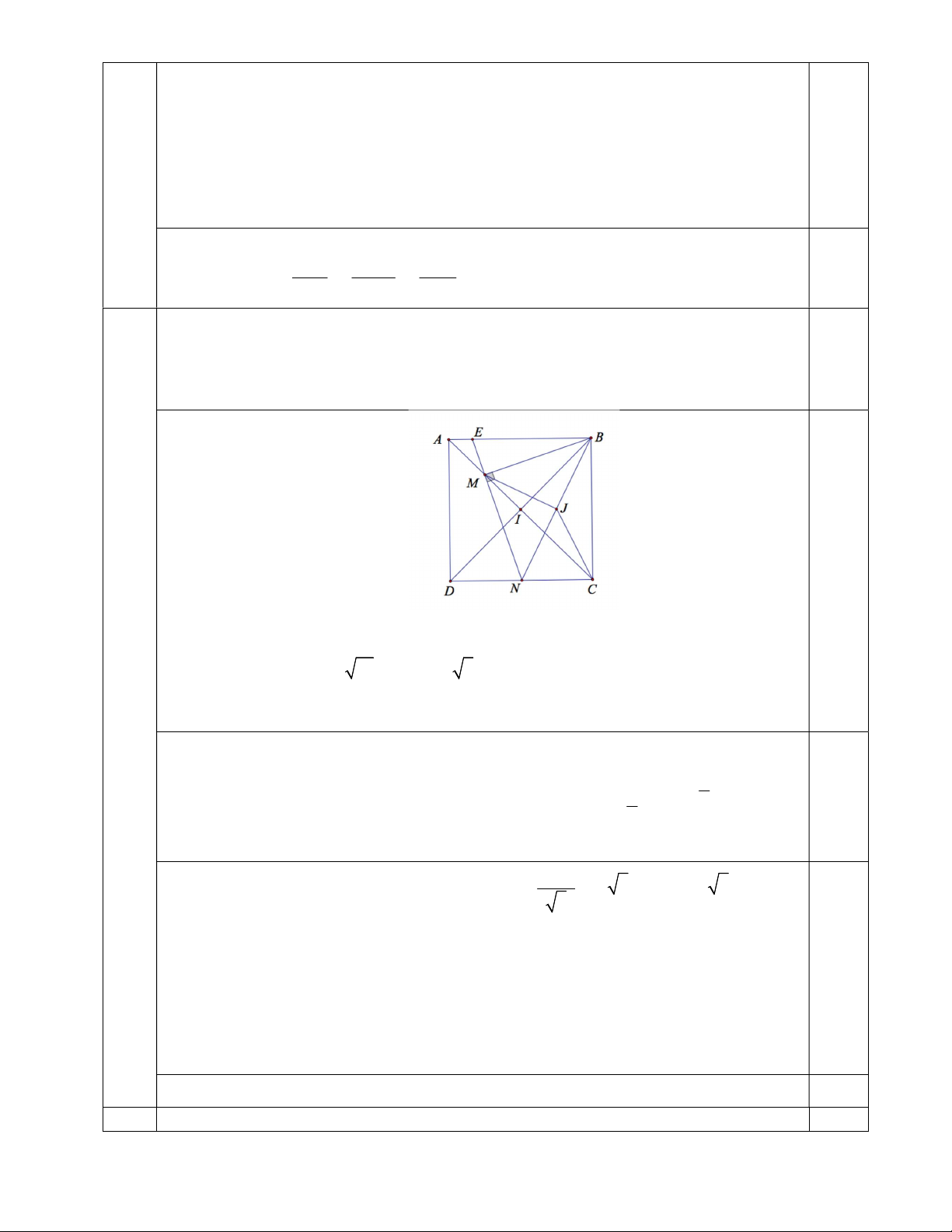
Trong mặt phẳng với hệ trục toạ độ Oxy cho hình vuông ABCD tâm I . Gọi M,N,J lần
lượt là trung điểm các đoạn thẳng AI,C ,
D BN . Biết phương trình đường thẳng MJ là y 2  7  0 1,0 và N 5; 
6 . Biết đỉnh C có hoành độ lớn hơn 3 . Tìm tọa độ đỉnh C của hình vuông ABCD . 0,25
Gọi độ dài cạnh hình vuông là 4a .
Dùng định lý hàm số côsin cho các tam giác ABM,CMN,BCN tính được: 2 2 2
MB  MN  a 10, BN  2a 5  BN  MB  MN . 6
Nên tam giác BMN vuông cân tại M và J là trung điểm của BN suy ra MJ  NJ .
Đường thẳng NJ đi qua N và vuông góc với MJ có phương trình là x  5  0  x   5 x   5  0     7
Toạ độ điểm J là nghiệm của hệ:    7  J 5  ;  2  y  7  0 .  y   0,25     2  2
Vì J là trung điểm BN nên B 5;  1 . 2BN
Gọi C x;y, x  3. Ta có: BC  2NC   2 5  NC  5 . 5 Ta có hệ phương trình: x   2 5  y  2 1  20
x 52 y  2 1  20 0,25     x   2 5  y  2 6  5 1  0y  35  15  x  2 5  4 x  7,y  5     y   5   x  3,y  5   
Đối chiếu điều kiện ta có C 7;5. 0,25 7 Cho a, ,
b c là các số thực dương. Tìm giá trị nhỏ nhất của biểu thức: 1,0 5
3b c 4a  3c 12b c T    2a 3b 2a  3c 3b 2a   2a 2a        3c 3c 12          b c         Ta có T 5                  4 2a 3b
3b 2a  2a 3b  2a  3c     0,25 3b 2a     1 1  4 2a  3b =       2a  3c         . 2a 3b    2a 3b 2a  3c 3a 2b 3a 2b
Áp dụng bất đẳng thức AM-GM ta có   2 .  2. 2b 3a 2b 3a 0,25 1 1 4 1 1 4 Áp dụng BĐT   với x,y  0 ta có   . x y x  y 2a 3b 2a  3b 2a  3c 2a  3b Suy ra T  5  2  4       2  4.2  10 .
2a  3b 2a  3c 0,25 Vậy T  5 .
Dấu "  " xảy ra khi 2a  3b  3 .
c Vậy giá trị nhỏ nhất của T là 5 0,25
------------------- Hết ------------------- Lưu ý khi chấm bài:
- Đáp án chỉ trình bày một cách giải bao gồm các ý bắt buộc phải có trong bài làm của học sinh. Khi chấm
nếu học sinh bỏ qua bước nào thì không cho điểm bước đó.
- Nếu học sinh giải cách khác, giám khảo căn cứ các ý trong đáp án để cho điểm.
- Trong bài làm, nếu ở một bước nào đó bị sai thì các phần sau có sử dụng kết quả sai đó không được điểm.
- Học sinh được sử dụng kết quả phần trước để làm phần sau.
- Trong lời giải bài hình, nếu học sinh không vẽ hình thì cho tối đa một nửa số điểm. Nếu học sinh vẽ sai hình thì không cho điểm.
- Điểm toàn bài tính lẻ đến 0,25 và không làm tròn. 6
Document Outline

• ĐỀ HSG MÔN TOÁN LỚP 11 năm học 2023-2024
• HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM MÔN TOÁN 11-2024