Đề thi chọn HSG Toán 11 năm học 2019 – 2020 trường THPT thị xã Quảng Trị

SỞ GD&ĐT QUẢNG TRỊ KỲ THI CHỌN HSG VĂN HÓA LỚP 11
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ Khóa thi ngày 12 tháng 6 năm 2020 Môn thi: TOÁN ĐỀ THI CHÍNH TH ỨC
Thời gian làm bài: 180 phút, không kể thời gian giao đề (Đề có 01 trang) 3
 x 1  x 1   Câu I. khi x 0
(5,5 điểm) 1.Cho hàm số f  x   x
. Tìm m để hàm số f x liên tục tại m2 khi x  0 x  0.
2. Một tổ gồm 10 học sinh gồm 6 học sinh nam và 4 học sinh nữ trong đó có hai học sinh nữ tên Trang
và Thủy. Xếp ngẫu nhiên 10 học sinh trên thành một hàng ngang. Tính xác suất để xếp được một hàng
ngang mà hai học sinh nữ Trang và Thủy luôn đứng cạnh nhau, đồng thời các học sinh nữ còn lại
không đứng cạnh nhau và cũng không đứng cạnh Trang và Thủy.
Câu II. (7,0 điểm)
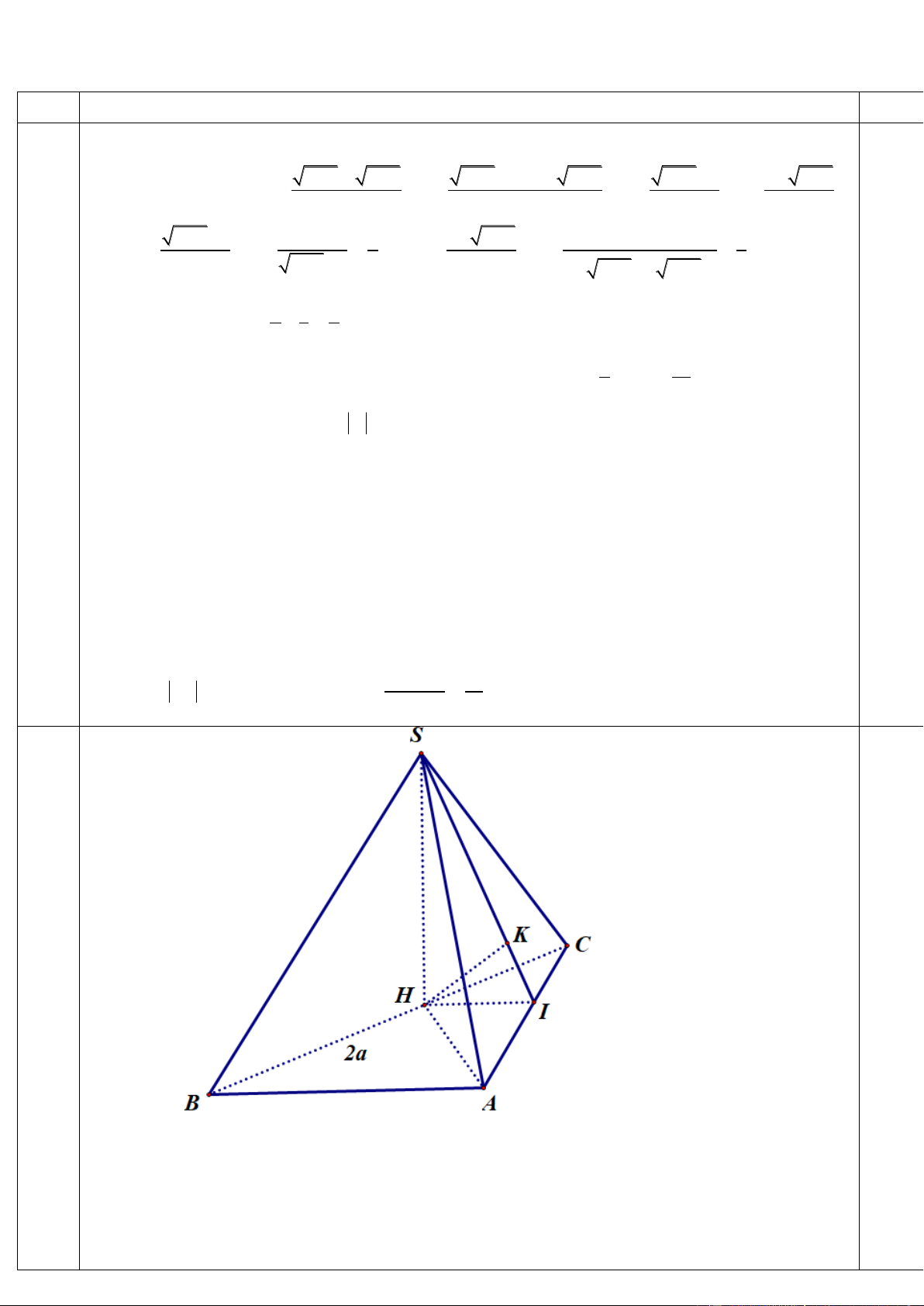
1. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A , 0
ABC  30 và BC  2a . Gọi H là
hình chiếu vuông góc của A lên BC . Biết hai mặt phẳng SHA và SBC cùng vuông góc với mặt
phẳng  ABC, đồng thời SA tạo với mặt phẳng  ABC một góc bằng 0 60 .
a) Tính góc tạo bởi SA và mặt phẳng SBC.
b) Tính khoảng cách từ B đến mặt phẳng SAC theo . a
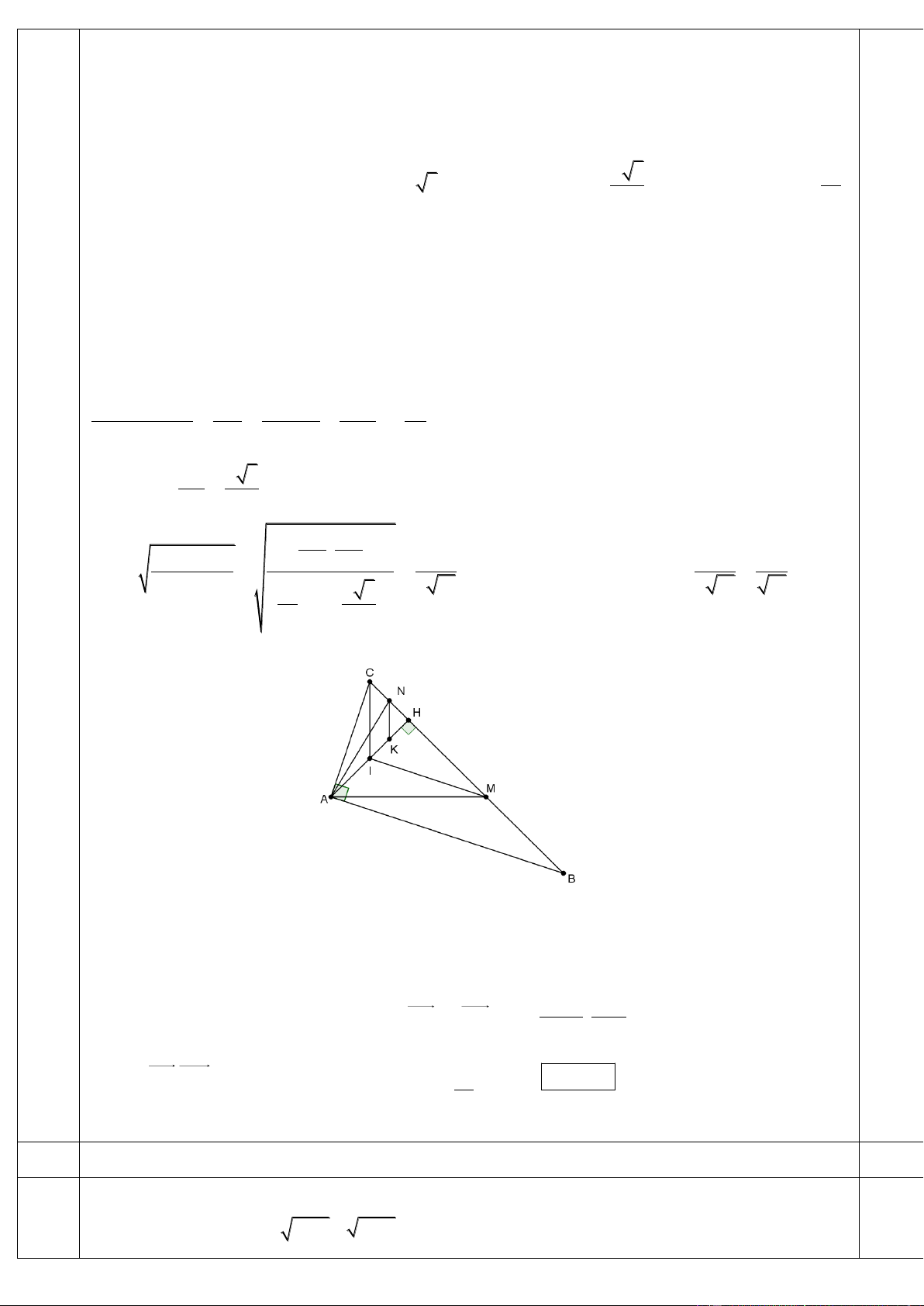
2. Trong mặt phẳng Oxy , cho tam giác ABC vuông tại .
A Gọi H là hình chiếu vuông góc của A trên
BC , các điểm M, N lần lượt là trung điểm của HB và HC ; điểm K là trực tâm tam giác AMN.
a) Gọi I là trung điểm của AH . Chứng minh rằng K là trung điểm của IH . b) Tìm tọa độ điểm  1 1 
A ; biết M 2;1, K  ; 
 và điểm A nằm trên đường thẳng x  2y  4  0 đồng  2 2 
thời điểm A có tung độ âm. 3 3
4x  y  x  y  3xy  2x  y
Câu III. (4,0 điểm) 1. Giải hệ phương trình sau trên tập số thực  . 2
 3 y  2  x  x y  xy  4x 1 
2. Tìm tất cả các giá trị thực của tham số m để phương trình     x   2 sin
1 .2sin x  2m  3sin x  m  2  0  
có đúng 4 nghiệm phân biệt thuộc đoạn 3 ;   .  6 2  u   4 1 
Câu IV. (3,5 điểm) 1. Cho dãy số u xác định bởi 2  3 . n u 2n  6n  3 . Xác định công n  n u   , n  1 n 1   n 1 n .n   3 2 1 thức tổng quát  n u 
u theo n và tính . lim n . n    4n 
2. Cho x , y , z là các số thực dương và thỏa mãn 2 2 2
x  y  z  2x . z x a) Chứng minh rằng  . y 1 x  y
x 2y  z  2  z 4y  3 2
b) Tìm giá trị lớn nhất của biểu thức 3x P    .
x  2 y   1  y   1 x  y2
--------------------HẾT---------------------
Thí sinh không được sử dụng tài liệu và MTCT (đối với môn Toán).
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:……………………………….Số báo danh:……………….
HƯỚNG DẪN CHẤM HSG 11 NĂM HỌC 2019-2020. CÂU NỘI DUNG ĐIỂM
1. (2,5 điểm). TXĐ D   1
 ;  , x  0D và f 0  m  2. 0,5             Ta có f  x 3 3 3 x 1 x 1 x 1 1 1 x 1 x 1 1 1 x 1 lim  lim  lim  lim  lim . 0,5 x0 x0 x0 x0 x0 x x x x x 1 1 1 1 3 1 x 1 1 1 lim  lim  và lim  lim  . 2 0,5 x0 x0 x x 1 1 2 x0 x0 x 3
 x    3 x   3 1 1 1 1 1 5
Suy ra lim f  x    . 0,5 x0 2 3 6 Hàm số 5 17
f  x liên tục tại x  0  lim f  x  f 0  m  2   m  . 0,5 Câu I x 0  6 6 (5,5
2. (3,0 điểm). Không gian mẫu   10!. 0,5 điểm)
-Gọi A là biến cố xếp được theo yêu cầu bài toán.
-Xếp 6 học sinh nam có 6! cách xếp. Mỗi cách xếp 6 học sinh nam ta xem mỗi học sinh nam là một 0,5
vách ngăn tạo ra 7 vị trí trống bao gồm 5 vị trí trống ở giữa và 2 vị trí trống ở hai đầu hàng.
-Số cách xếp hai bạn nữ Trang và Thủy cạnh nhau là 2!
-Hai hs nữ Trang và Thủy luôn cạnh nhau nên xem 2 bạn như 1 bạn và 2 bạn nữ còn lại ta có 3 bạn 0,5 nữ.
-Số cách xếp sao cho hai bạn nữ còn lại không cạnh nhau và không cạnh Trang và Thủy là 3 A . 7 0,5 Khi đó, 6!.2!.A 1 3
  6!.2!.A . Vậy p A 3 7   . A 7 10! 12 1,0 1. (5,0 điểm) Câu II (7,0 điểm)
SHASBC  SH  
a) (2,5 điểm). (Ta có SHA   ABC 
  SH   ABC và AH   ABC nên SH  AH   1 0,5  
SBC    ABC  
Mặt khác AH  BC (2)
Từ (1) và (2) suy ra AH  SBC, suy ra hình chiếu vuông góc của SA lên mặt phẳng SBC là SH . 0,5 Do đó, S ,
A SBC  S ,
A SH   ASH (vì tam giác SHA vuông tại H ). 0,5
Theo gt SA  ABC  SA AH  0 0 , ,
 SAH  60  ASH  30 . Vậy SA SBC 0 ,  30 . 1,0 a 3 3a
b) (2,5 điểm).Ta có 0 0 0
AB  BC.cos 30  a 3  AH  A . B sin 30 
 SH  AH.tan 60  2 2 và AC  . a
Gọi I là hình chiếu vuông góc của H lên AC , suy ra AC  SHI   SAC  SHI  và 0,5 
SHI  SAC  SI .
Trong tam giác SHI kẻ HK  SI  HK  SAC hay d H;SAC  HK . 0,5 Mặt khác . d  ; B SAC  2 2 2 BC BC BC  2a            d  4 d ; B SAC 4d H ; SAC 4HK. 2     H ;SAC      HC HC.BC AC  a  0,5 Ta có AB a 3 HI  
. Trong tam giác vuông SHI ta có 4 4 2 2 9a 3a 2 2 . SH .HI 3 1,0 4 16 a a a HK   
. Vậy d B SAC 3 6 ;  4HK  4.  . 2 2 2 2 SH  HI     2 13 3a a 3 2 13 13       2  4   2. (2,0 điểm)
a)(1,0 điểm). I là trung điểm của AH , ta có MI / / AB  MI  AC  I là trực tâm tam giác 0,5
AMC  CI  AM .
Mặt khác NK  AM  NK / /CI  K là trung điểm của HI. 0,5
 2a  2 2  a 
b) (1,0 điểm).Giả sử 0,5 A 2
 a  4;a, từ AK  3KH  H ;    3 3   a  1  Lại từ 2 AK.MH 0 10a 13a 23 0        0,5    A   a lo¹i  2; 1 23   10 3 3
4x  y  x  y  3xy  2x  y (1) 1.(2,5 điểm).  2
 3 y  2  x  x y  xy  4x 1 (2)  x  2  1) Điều kiện  . y  3
(1)  2x  y3  2x  y 3  y  y
 2x  y  y2x  y2  y2x  y 2
 y  1  x  .y 0,5
Thay x  y vào phương trình 2 ta được: 3 2
3  x  2  x  x  x  4x 1   x  5   x  4 
x  5 x  4 3 2  3  x   2  x 
 x  x  4x 1  (*)      0,5 3   3  3 3   x  5    3 x 0  Với 3 2
  x  3, ta có  x  4  2  x   0 Câu  3   III 2 2 1  x  x  2
x  x  2  (*)       2
x  x  2x  2 (4,0 9 x  5 x  4  3  x  2  x   điểm)  3 3       1 1  2
x  x  2 
 9x  2  0  0,5 x  5 x  4  3 x  2  x    3 3  2
x  x  2  0  1 1   
 9x  2  0 vn do VT  0, x   2  ;  3   0,5 x  5 x  4 3  x  2  x   3 3  x  1   y  1  . 2
 x  x  2  0  
x  2  y  2. 0,5
Vậy hệ phương trình đã cho có hai nghiệm  ; x y là  1  ;  1 và 2; 2 . 2) (1,5 điểm). sin x 1 0,5   sin x   1 2
1 . 2sin x  2m  3sin x  m  2  0  sin x     2
sin x  m  2      0,5
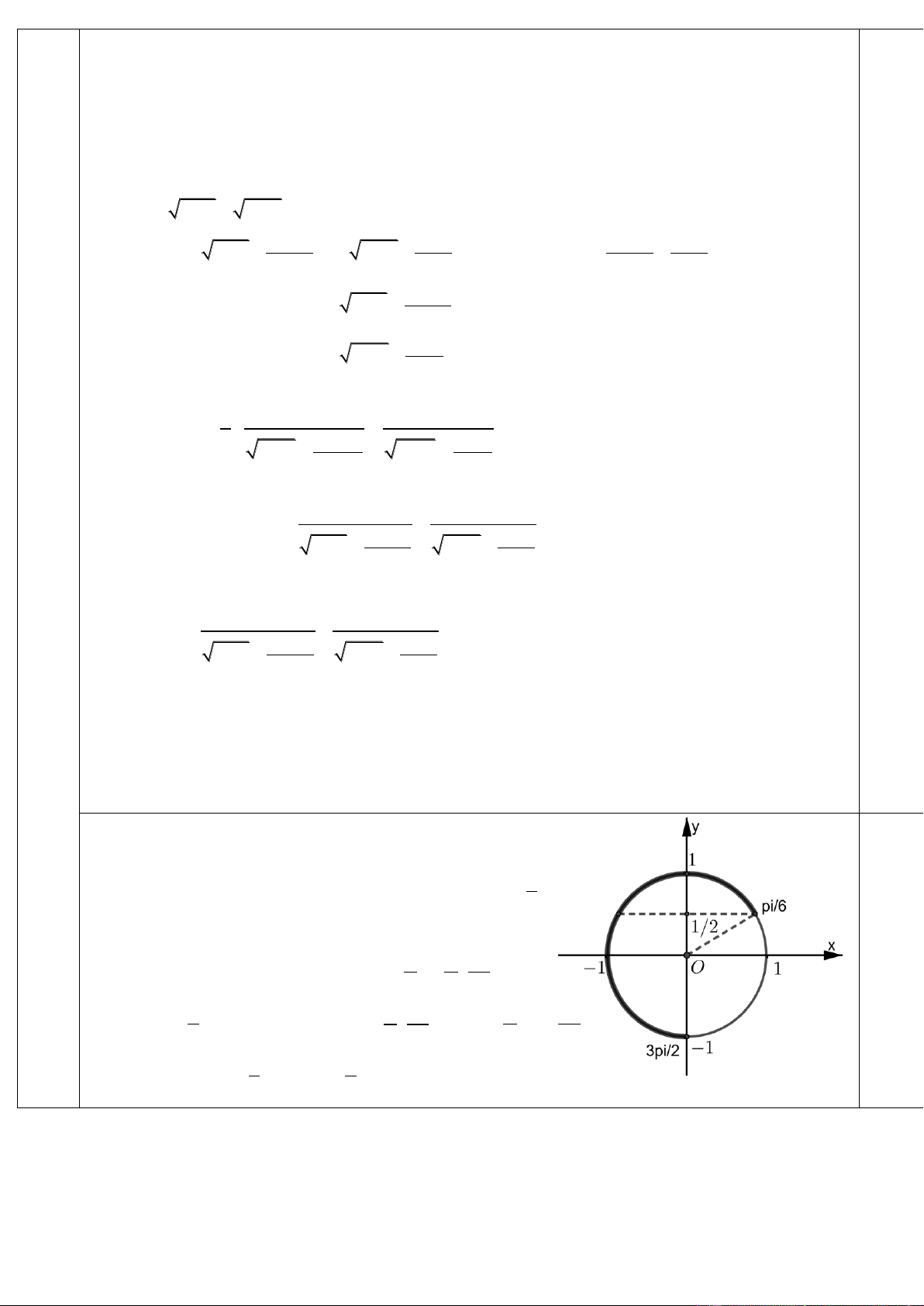
+) pt sin x 1 có đúng một nghiệm 3 x   ;   2  6 2  1      +) pt sin x  có đúng 2 nghiệm 3  ;   là 5 x  ; x  . 2  6 2  6 6 0,5 1 5 Ycbt  1
  m  2   1 m  . 2 2
1) (1,5 điểm) Ta có: 2 3 . n u 2n 6n 3 2n 6n 3  3 1      n u  
 n 1 .u  3 . n u 
 n 1 .u  3 . n u     n 3   2 1 n 1  n 2    n 1 n n n .n   1 n .n   1 2 2 2 1  n n   2 1       n   1 1 1 .u   3 . n u  , n  1. n 1     n  2 n 2 1  n  0,5 v  3 Đặt 1 v  . n u  , n
 1. Khi đó ta có dãy v xác định bởi 1  n  n n 2 n v  3v , n  1.  n 1 n Suy ra dãy  n n 1 v
là cấp số nhân công bội q  3, suy ra 1
v  v .q  3  . n u   3n n  n 1 n 2 n 0,5 3n 1  u   , n  1 và n 3 n n n . n u  3 1      lim n  lim         0. 0,5 n 2  4   4  n .4n   2) (2,0 điểm). 2 2 2 2 2
a) (0,5 điểm). Ta có x  y  z  2x  2x  2xy   x  y  z  2 x  y z (1). 0,25     z x
x y 1   x  y z   . y 1 x  y
x 2y  z  2  z 4y  3 2 3x 2 x  z 2 z 3x 0,25
b)(1,5 điểm).Ta có P      
x  2 y   1  y   1
x  y2 x  2y 1 y 1 x  y2 z x
x  y z Câu Theo a)   y 1 . y 1 x  y x IV 0,5 x  y z x  y x  z (3,5
Khi đó x  y   x  y   y        2 1
1  x  y 
 x  2y 1 . x x điểm) 2 x  z
2 x  z x Ta được 2x   . x  2 y 1
x  yx  z x  y 0,5 2 x  z 2 2 Do đó z 3x 2x x 3x P       x  2 y 1 y 1
x  y2 x  y x  y x  y2 2 2 x  x  3  x 1  3  P  3.  3.   3       (2). x  y  x  y  4
 x  y 2  4 Vậy 3 P
 khi (1) và (2) đồng thời xảy ra 0,5 max 4
x  y  z  1 
x  y  z x  y  x 1     3     z  2x   . x  y 2 2    2 2 2      2 z x y z x  2 2 2       3 x y z 2x