TRƯỜNG TH-THCS-THPT VIỆT ÚC ĐỀ KIỂM TRA CUỐI HỌC KỲ I – NH: 2019-2020
---------- Môn: TOÁN – Lớp 11
Thời gian làm bài: 90 phút (không kể thời gian phát đề) (đề có 1 trang)
---------------------------------------- Đề bài Câu 1 (2 điểm)
Giải các phương trình sau: a) 2 4sin x  4sin x  3  0 b) cos 2x  3sin 2x  3 c) 2 2
5sin x  sin xcos x  4cos x  5 Câu 2 (3 điểm)
a) Từ các số {0; 1; 2; 3; 5; 6; 7; 8} lập được bao nhiêu số chẵn có 4 chữ số đôi một khác nhau. 5  2 
b) Tìm hệ số của số hạng chứa 10 x trong khai triển 3 x   2   x 
c) Lớp 11A có 35 học sinh gồm 15 nữ và 20 nam. Cần chọn ngẫu nhiên 6 bạn để tham gia
trồng cây tại rừng Cần Giờ. Tính xác suất để trong 6 bạn được chọn:
i/ số bạn nam bằng số bạn nữ.
ii/ có ít nhất 1 nam và ít nhất 1 nữ. u   2u  4u  137
Câu 3 (1.5 điểm) Cho cấp số cộng u n  1 7 10 : 5u u  2u  72  5 6 3
a) Tìm số hạng đầu và công sai của cấp số cộng trên.
b) Tính tổng S  u  u  u  ....  u 10 14 18 98
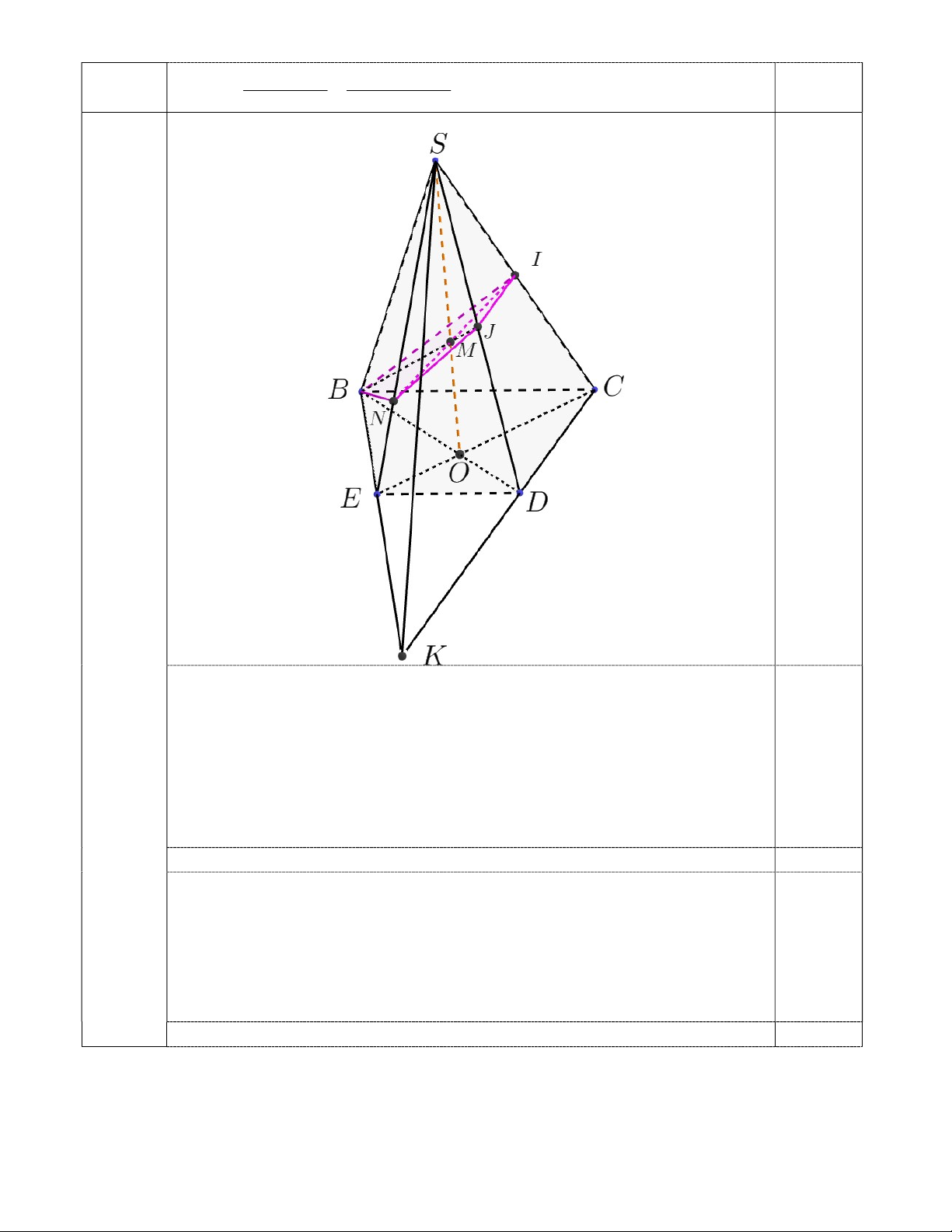
Câu 4 (3,5 điểm) Cho hình chóp S.BCDE có đáy là hình thang (với BC là đáy lớn, BC // ED ).
a/ Tìm giao tuyến của mặt phẳng (SBE) và (SCD); mặt phẳng (SBC) và (SED).
b/ Gọi I, J lần lượt là trung điểm của SC và SD . Chứng minh: CD // ( I B J) .
c/ Tìm giao điểm của BJ và mặt phẳng (SCE).
d/ Xác định thiết diện của mặt phẳng (BIJ) với hình chóp S.BCDE -----------Hết------------
Thí sinh không được sử dụng tài liệu.
Họ và tên học sinh:…………………………………….- Lớp:………
Số báo danh:…………………………………………………………..
TRƯỜNG TH-THCS-THPT VIỆT ÚC ĐÁP ÁN – THANG ĐIỂM
----------------------- Môn: TOÁN 11 Năm học: 2019-2020 ĐÁP ÁN - THANG ĐIỂM Câu Đáp án Điểm 1 a) 2
4sin x  4sin x  3  0 (0,5 điểm) ( 2,0  3 điểm) sin x  (l  do | sinx | 1)  2 2
4sin x  4sin x  3  0   0,25 1  sin x  (n)  2   x   k2 1  6  sin x    k  0,25 2 5 x   k2  6 b) cos 2x  3sin 2x  3 1 3 3   3  cos 2x  sin 2x 
 sin cos 2x  cos sin 2x  2 2 2 6 6 2    3  sin  2x    0,25  6  2      2x   k2 x    k  6 3  12     ;k   0.25+0,25    2x  k2      x    k  6 3  4 c) 2 2
5sin x  sin xcos x  4cos x  5 (0,75 điểm)  * TH1: cos x  0  x 
 k . Phương trình đã cho trở thành: 0 = 0 (luôn 2 0,25  đúng). Suy ra: x 
 k là nghiệm của phương trình. 2  * TH2: cos x  0  x 
 k . Phương trình đã cho tương đương với: 2 2 2
5tan x  tan x  4  5  5tan x 0,25  tan x  1   x   k (k  Z ) 0,25 4   Vậy 
S    k;  k , k  Z   2 4  2 1. (1,0 điểm)
(3 điểm) a) Goi số có 4 chữ số có dang abcd 0,25
Vì abcd là số chẵn nên d  {0;2;6;8} + TH1: d=0
a có 7 cách chọn ( a  0 ); b có 6 cạch chọn; c có 5 cách chọn; 0,25 Có 7.6.5 = 210 số
+ TH2: d  {2;6;8} => d có 3 cách chọn.
a có 6 cách chọn ( a  0 ; a  d ); b có 6 cách chọn; c có 5 cách chọn; 0,25 Có 3.6.6.5=540 số
Có thể lập đượ tất cả: 210+540=750 số. 0,25 2. (1.0 điểm) 5  2 
b) Tìm hệ số của số hạng chứa 10 x trong khai triển 3 x   2   x 
Xét số hạng thứ k+1, ta có: k   2 k  k  2k k k T  C x  C x k 1  5  3 5 35   2  5 2k 0,25  x  x  k 2k k 15 3 k k 155  C x .  C 2 k x 0,25 5 2k 5 x
Theo đề bài, ta có: 15  5k  10  k  1 0,25
Vậy hệ số cần tìm là: 1 1 10 10
T  C 2 x  10x => hệ số cần tìm là: 10 0,25 2 5 3. (1.0 điểm)
Số phần tử của không gian mẫu 6 n()  C 35 0,25
a/ Gọi biến cố A: ‘số bạn nam bằng số bạn nữ’. 3 3 n( ) A  C .C  518700 20 15 n( ) A 518700 3705 Khi đó: P( ) A     0,32 6 0,25 n() C 11594 35
b/ Gọi biến cố B: ‘ít nhất 1 nam và ít nhất 1 nữ’
B : ‘không có nam hoặc không có nữ’. 0,25 Khi đó: 6 6 n(B)  C  C  43765 20 15 43765 P(B)  1 P(B)  1  0,97 6 0,25 C35 3
a) Tìm số hạng đầu và công sai của cấp số cộng trên. (1,5 Ta có: điểm) u   2u  4u  137 u
  2 u  6d  4 u  9d  137 0,25 1 7 10  1  1   1     0,25 5u  u  2u  7  2  5
 u  4d  u  5d  2 u  2d  72 5 6 3   1   1   1   u   24d  137 u   7 1 1     6u  19d  72  d  6 1 0,5
b) Tính tổng S  u  u  u  ....  u 10 14 18 98
Ta có: u  u  9d  7  9. 6  4
 7 ; u  u  97d  7  97. 6   5  75 98 1   10 1    Số các số hạng: 98 10 n  1  23 0,25 4 nu  u 23 47  575 0,25 10 98    Vậy S    7153 2 2 4 (3,5 điểm) a/  Tìm (SBE) (SCD) = ?
Trong (BCED) , gọi K  BE CD Ta có: S  (SBE)  (SCD) (1) 0,25 K  BE  (SBE)   K (SBE)  ( C S D) (2) K CD  (SCD) 0,25
Từ (1) và (2) suy ra (SBE)  (SCD)  SK 0,25  Tìm (SBC)  (SED) = ? Ta có: S (SBC)  (SED)  BC  (SBC) 0,25  ED  (SED)  BC/ / E D
Suy ra (SBC)  (SED)  Sx // BC // ED . 0,25 b/ Chứng minh: CD // (BIJ) Ta có: IJ / / CD
(vì IJ là đường trung bình của SCD )  C  D  (BIJ) 0,5 IJ  (BIJ)   CD // (BIJ) . 0,25
c/ Tìm giao điểm BJ  (SCE) = ?  Xét (SB ) D  (SCE)
Trong ( ABCD ), gọi O  BD CE . Ta có: S  (SBD)  (SCE) (1) O   BD  (SBD)   O (SBD)  (SCE) (2) O  CE  (SCE) 0,25
Từ (1), (2) suy ra (SBD)  (SCE)  SO 0,25
 Trong (SBD), gọi M  BJ  SO M  BJ  Ta có: M  SO  (SCE)  M  BJ  (SCE) 0,25 d/ Tìm giao tuyến:
Trong ( SEC ), gọi N  IM  SE 0,25 Khi đó: (BIJ)  (SBC)  BI (BIJ )  (SCD)  IJ 0,25 (BIJ)  (SED)  JN (BIJ)  (SBE)  NB
Vậy thiết diện của (BIJ) và hình chóp S.BCDE là tứ giác BIJN. 0,25
Ghi chú: Học sinh giải theo cách khác đúng. Giáo viên theo thang điểm trên cho điểm.