


Preview text:
TRƯỜNG THPT ĐÔNG HÀ
ĐỀ KIỂM TRA CUỐI KỲ I – NĂM HỌC 2020 - 2021 TỔ: TOÁN
MÔN TOÁN – LỚP 11
(Đề gồm 01 trang)
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Họ và tên:……………………………………….. .......Lớp:….…………SBD:……...…
Câu 1 (3.0 điểm). Giải các phương trình sau:
a. 2sin 2x −1= 0. b. 2
2sin x − 3cos x + 3 = 0.
c. 2sin 2xcos x −sin x = 2 + 3 cos3x. d. 2 2021π 2 2021 2sin x 2cos x π − − + + tan x = 0. 4 2
Câu 2 (1.0 điểm). Từ tập A = {1;2;3;4;5;6;7; }
8 có thể lập được bao nhiêu số tự nhiên có 4
chữ số đôi một khác nhau và chia hết cho 5?
Câu 3 (1.0 điểm). Tìm hệ số của số hạng chứa 6
x trong khai triển của nhị thức 15 (x − 2) .
Câu 4 (2.0 điểm). Một lớp học có 18 học sinh nam và 20 học sinh nữ. Lớp trưởng chọn ngẫu
nhiên 4 bạn tham gia cùng một trò chơi. Tính xác suất để sao cho:
a. trong bốn bạn được chọn có 2 bạn nam, 2 bạn nữ.
b. trong bốn bạn được chọn không có quá 3 bạn nam.
Câu 5 (1.0 điểm).Trong mặt phẳng tọa độ Oxy , cho điểm M ( 2; − 3) và đường thẳng
d : 2x −3y + 6 = 0 .
a. Tìm tọa độ điểm M’là ảnh của điểm M qua phép tịnh tiến theo u (3,4) .
b. Tìm ảnh của đường thẳng d qua phép đối xứng tâm O(0;0) .
Câu 6 (2.0 điểm). Cho hình chóp S.ABCD , có đáy ABCD là hình thang với đáy lớn AB , gọi
M là trung điểm của SA , E là điểm trên cạnh AB sao cho tứ giác AECD là hình bình hành,
I là trung điểm của CE. Gọi (α ) là mặt phẳng chứa IM và song song với . SD
a. Tìm giao tuyến của hai mặt phẳng (SAD)và (SBC).
b. Tìm giao điểm N của đường thẳng AD và mặt phẳng (α ) .
c. Giả sử tam giác SCD cân tại S . Chứng minh rằng thiết diện của hình chóp S.ABCD
cắt bởi mặt phẳng (α ) là một hình thang cân. …..HẾT…..
TRƯỜNG THPT ĐÔNG HÀ
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KÌ I TỔ TOÁN
NĂM HỌC: 2020 – 2021 MÔN: TOÁN - LỚP 11 Câu Nội dung Điểm 1
pt ⇔ sin 2x = . 0.25 2 π ⇔ = sin 2x sin . 0.25 6 π 2x = + k2π 6 0.25 1a ⇔ . π
2x = π − + k2π 6 π x = + kπ 12 0.25 ⇔ ,k ∈ . 5π x = + kπ 12 pt ⇔ ( 2
2 1− cos x) −3cos x + 3 = 0 . 0.25 2 ⇔ + − = . 0.25 2cos x 3cosx 5 0 1b cosx =1 ⇔ 5 . 0.25
cosx = − (PTVN) 2
⇔ x = k2π ,k ∈ . 0.25
pt ⇔ sin 3x + sin x − sin x = 2 + 3 cos3x 0.25
⇔ sin 3x − 3 cos3x = 2 1c 1 3 π ⇔ sin 3x −
cos3x =1 ⇔ sin(3x − ) =1 2 2 3 π π 5π k2π 0.25
⇔ 3x − = + k2π ⇔ x = + , k ∈ . 3 2 18 3 π
Điều kiện: cos x ≠ 0 ⇔ x ≠ + k , π k ∈ . 2 π π 1d 2 2
pt ⇔ 2sin x − 505π − − 2cos x +1010π + + tan x = 0 4 2 π 2 2 sin ⇔ 1− cos 2 − = 2sin − tan ⇔ 1− sin 2 = 2sin x x x x x x − 0.25 2 cos x 2
2sin xcos x − sin ⇔ 1− sin 2 x x =
⇔ 1− sin 2x = tan x(sin 2x − ) 1 cos x
⇔ (1− sin 2x)(1+ tan x) = 0 π sin 2 = 1 x = + l x π 4 ⇔ ⇔ ,l ∈ . tan x = 1 − x π = − + lπ 4 0.25 π π
Đối chiếu điều kiện vậy phương trình có nghiệm là m x = + ,m∈ . 4 2
Gọi số cần tìm là abcd 0.25 Chọn d có 1 cách 0.25 2
Chọn a, b, c có 3 A7 cách 0.25 Vậy có tất cả 3 1.A = 210 số. 0.25 7 15 k 15 0.5 15 k 15−k k k 15−
Ta có: (x − 2) = ∑C x .( 2) − = ∑C ( 2) k − x . 15 15 3 k=0 k=0 Vì số hạng chứa 6
x nên: 15 − k = 6 ⇔ k = 9 . 0.25
Hệ số của số hạng chứa 6 x là 9 9 C ( 2) − = 2562560 − . 0.25 15
Số phần tử của không gian mẫu: 4
Ω = C = 73815. 0.5 38
Gọi A là biến cố “trong bốn bạn được chọn có 2 bạn nam, 2 bạn nữ”. 4a
Số các kết quả thuận lợi cho biến cố A là: 2 2 Ω = C C = . A . 29070 18 20 0.25 2 2 Ω ⇒ P( A) A C .C 102 18 20 = = = . 4 Ω C 259 0.25 38
Gọi B là biến cố “trong bốn bạn được chọn không có quá 3 bạn nam”. 0.25
Số các kết quả thuận lợi cho biến cố B là: 4 1 3 2 2
Ω = C + C C + C C + C C . 0.5 B . . 3 1 . 4b 20 18 20 18 20 18 20 4 1 3 2 2 3 1 Ω + + + ⇒ P(B) B C C .C C .C C .C 4717 20 18 20 18 20 18 20 = = = . 4 Ω C 4921 0.25 38 Gọi M’( ’; x ’
y ), T (M ) = M ' ⇔ MM ' = u . 0.25 5a u
x ' = x + a = 2 − + 3 =1 ⇔ ⇒ M '(1;− ) 1 .
y ' = y + b = 3 − 4 = 1 − 0.25
Gọi d ': 2x −3y + c = 0 là ảnh của d phép đối xứng tâm O(0;0).
Lấy M (0;2)∈d . Ảnh của M qua phép đối xứng tâm O là M '(0; 2 − ). 0.25 5b M '(0; 2
− )∈d ' ⇔ 2.0 − 3.( 2)
− + c = 0 ⇔ c = 6 − . 0.25
Vậy ảnh của d qua phép đối xứng tâm O là d ': 2x−3y−6 = 0. S
Ta có: S ∈(SAD) ∩(SBC) . (1) 0.25
Gọi F = AD ∩ BC . 0.25
F ∈ AD ⇒ F ∈(SAD) Q
F ∈ BC ⇒ F ∈(SBC) 0.25 M 6a
⇒ F ∈(SAD) ∩ (SBC) . (2) Từ (1) và (2) suy ra: A E
(SAD) ∩ (SBC) = SF . 0.25 N B D I P C F
M ∈(α ) ∩(SAD) M ∈ d Ta có ( α ) // SD
, gọi d = (α )∩(SBC) ⇒ . 0.25 d // SD 6b SD ⊂ (SAD) N ∈ AD N ∈ AD
Gọi N = d ∩ AD , khi đó ⇒
⇒ N = AD ∩(α ) . N d, d (α ) ∈ ⊂ N ∈ (α ) 0.25
Kẻ NI cắt CB tại P . Do MN // SD và M là trung điểm SA nên N là trung
điểm của AD . Điểm I là trung điểm CE nên NP là đường trung bình của hình
thang ABCD . Lúc đó, NP // AB nên (α )// AB. 0.25
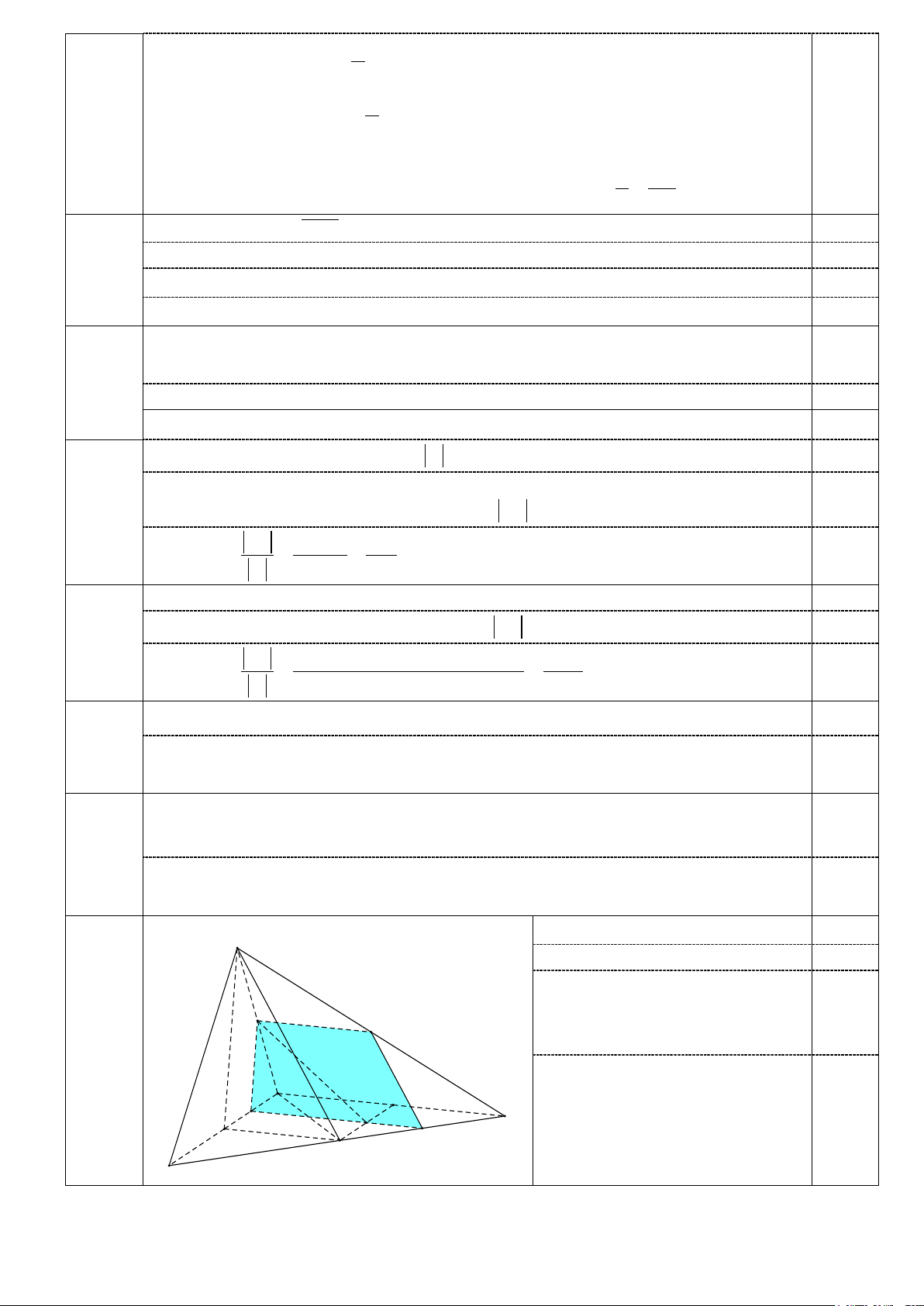
Từ đó, kẻ MQ song song với AB, Q∈SB . Thiết diện diện hình chóp cắt bởi (α )
là hình thang MNPQ (vì NP // AB, MQ // AB ).
Do NP là đường trung bình của hình thang ABCD , suy ra 1
NP = ( AB + CD) . 6c 2
Do MQ là đường trung bình của tam giác SAB nên 1 MQ = AB . 2 0.25
Suy ra NP > MQ do đó MNPQ là hình thang không là hình bình hành. (3) Mặt khác, 1 1 MN = ;
SD PQ = SC mà SC = SD suy ra MN = PQ . (4) 2 2
Từ (3) và (4) suy ra MNPQ là hình thang cân.
Lưu ý: Học sinh có thể làm bài theo phương pháp giải khác có kết quả đúng thì vẫn
được đánh giá điểm đã cho tương đương cho phần nội dung trả lời đó.
Document Outline
- DE KIEM TRA HOC KI 1_KHOI 11_2020-2021
- DAP-AN-DE-KIEM-TRA-HOC-KI-1_KHOI-11_2020-2021




