Đề thi giữa kì 2 Toán 11 năm 2020 – 2021 trường Phan Đình Phùng – Hà Nội

TRƯỜNG THPT PHAN ĐÌNH PHÙNG
ĐỀ KIỂM TRA GIỮA HỌC KÌ II, NĂM HỌC 2020-2021 TỔ TOÁN - TIN Môn: Toán - Lớp 11
Thời gian làm bài 60 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (Đề có 03 trang) Mã đề 123
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD: . . . . . . . . . . . . . .
Ghi chú: Phần trắc nghiệm làm trên phiếu được phát, nộp phiếu trả lời trắc nghiệm sau khi hết 30 phút
đầu. Phần tự luận làm trên giấy được phát.
PHẦN 1: TRẮC NGHIỆM (Thời gian làm bài: 30 phút) (5,0 điểm, mỗi câu 0,25 điểm)
Câu 1: Cho cấp số nhân 4, − x, 9 − . Khi đó 2 x bằng: 13 − 169 A. . B. 6 C. 36 . D. . 2 4
Câu 2: Cho cấp số cộng (u ) có u = 1 và u = 59 . Khi đó công sai của cấp số cộng bằng: n 1 2 A. 57 . B. 58 − . C. 58 D. 56 .
Câu 3: Cho hình chóp S.ABC , cạnh bên SA vuông góc với đáy, BI vuông góc với AC tại I . Khẳng
định nào sau đây đúng?
A. BI ⊥ SC .
B. BI ⊥ (SBC ) .
C. BI ⊥ SB .
D. BI ⊥ (SAB) .
Câu 4: Cho tứ diện ABCD có AB = CD = AD = 2, AC = BD = 3 và BC = 1. Mệnh đề nào sau đây đúng A.  0 (CD, CB) = 90 B.  0 (CD, AD) = 90 . C.  0 (C , A AD) = 90 D.  0 ( , CA CB) = 90 . *
Câu 5: Cho dãy số (u = = n ∀ ∈
n) xác định bởi u 1, u 2 . n u  . 1 n 1 + n
Giá trị của u là: 5 A. 2048 B. 32 C. 160 D. 1024 1 − n
Câu 6: Cho dãy số (u ) với u = . Khi đó u bằng: n n n 1 7 2 + 6 − 6 − 7 − 6 − A. u = . B. u = . C. u = . D. u = 7 7 2 7 8 2 7 7 2 7 6 2 Câu 7: lim ( 2
−x − 3x + 2) có giá trị bằng x 1 →− A. 6 . B. 4 . C. 1 − . D. −∞ . 2x +1
Câu 8: Cho hàm số y =
. Tìm mệnh đề sai? x −1 1 A. lim y = .
B. lim y = +∞ .
C. lim y = +∞ . D. lim y = 2 . x→ 1 − 2 − + x 1 → x 1 → x→+ ∞
Câu 9: Cho cấp số cộng (u ) có u = 12 và tổng 9 số hạng đầu tiên là S = 504 . Khi đó u bằng: n 9 9 1 A. 55 . B. 124 . C. 50 D. 100 .
Câu 10: Cho hình lập phương ABCD.A' B 'C ' D '. Vectơ nào dưới đây là vectơ chỉ phương của đường thẳng AC ?    
A. A 'C . B. AB . C. AB ' . D. A 'C ' Mã đề 123-Trang 1/3
Câu 11: Cho dãy số 1,2,3,-4,5,7,8,9,110. Khẳng định nào sau đây đúng ?
A. Dãy tăng và bị chặn.
B. Dãy không bị chặn.
C. Dãy giảm và bị chặn.
D. Dãy số không tăng, không giảm.
Câu 12: Cho hình hộp ABC .
D A' B 'C ' D ' tâm O. Mệnh đề nào sau đây sai?
   
   
A. AB + AD + AA ' = 2 AO .
B. AB + AD + AA ' = 0 .
    
   
C. OA + OB + OC ' + OD ' = 0 .
D. AB + AD + AA ' = AC ' .  
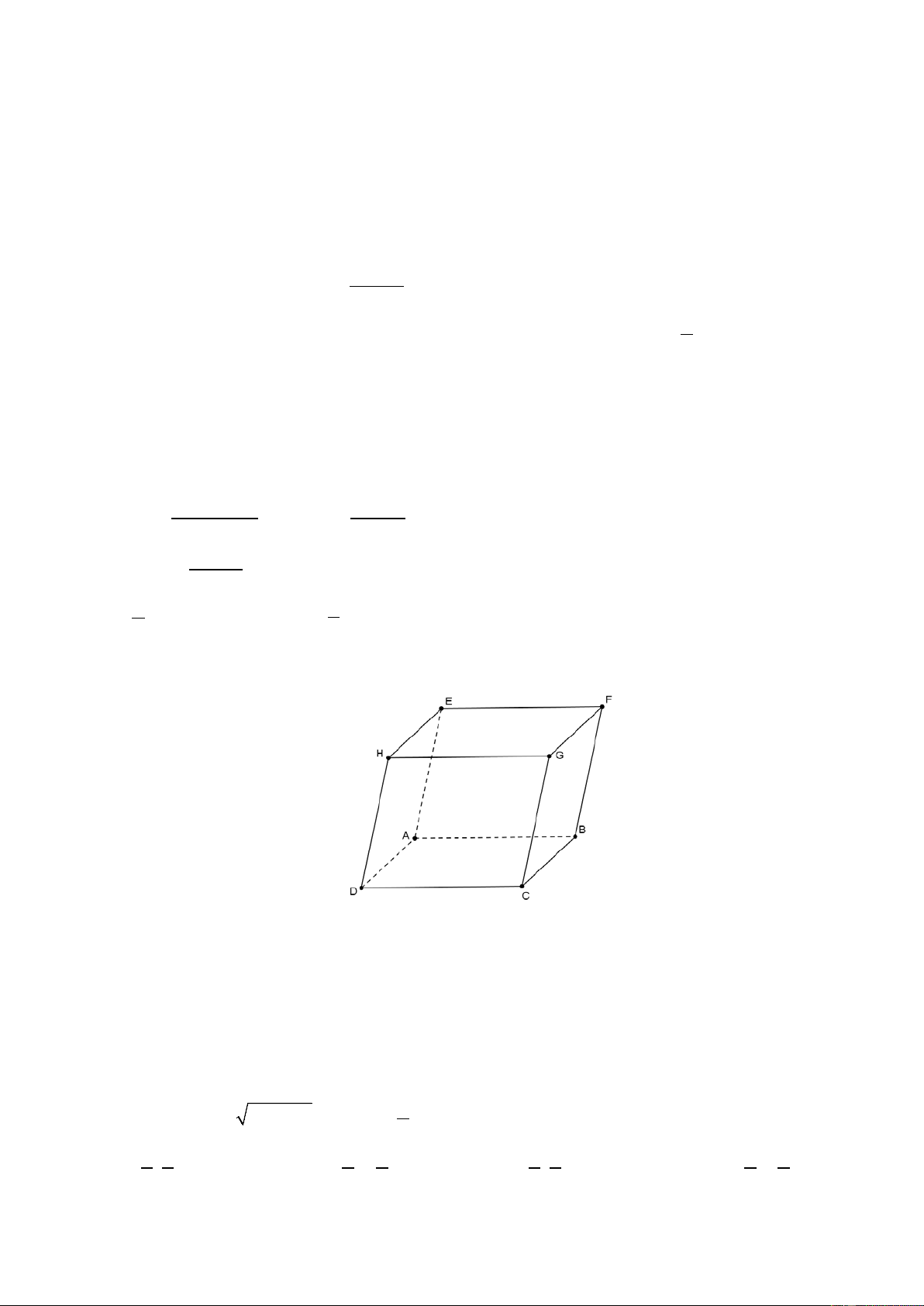
Câu 13: Cho hình lập phương ABC .
D EFGH . Hãy tính góc giữa cặp vectơ AB và EG A. 45 . B. 60 . C. 90 . D. 120 . n −
Câu 14: Cho dãy số (u ) biết 2 13 u =
. Khẳng định nào sau đây đúng? n n 3n − 2 A. Dãy số giảm.
B. Dãy bị chặn dưới bởi 2 . 3
C. Dãy số không tăng, không giảm. D. Dãy số tăng.
Câu 15: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O . Biết SA = SC và SB = SD .
Khẳng định nào sau đây sai?
A. AC ⊥ SD .
B. SO ⊥ ( ABCD) .
C. CD ⊥ (SBD) .
D. BD ⊥ SA .
Câu 16: Dãy số nào sau đây có giới hạn là +∞ ? 2 2n + 2n −1 2 n − 2n A. u = . B. u = . C. 2 3
u = 3n − 4n . D. 2
u = 3n −13n . n 3 n + 4 n 2 − n n n 2 7n − 3 Câu 17: lim bằng 2 n − 2 3 3 A. B. − C. 7 − D. 7 2 2
Câu 18: Cho hình hộp ABC .
D EFGH . Khẳng định nào sau đây đúng?   
A. Ba véctơ EH , EF và AC đồng phẳng.   
B. Ba véctơ EH , EA và EF đồng phẳng.   
C. Ba véctơ GH ,GF và BG đồng phẳng.   
D. Ba véctơ EH , EF và AG đồng phẳng.
Câu 19: Cho hình lập phương ABC .
D A ' B 'C ' D ' có I , J tương ứng là trung điểm BC, BB ' . Góc giữa
hai đường thẳng AC và IJ bằng? A. 45 . B. 30 . C. 120 . D. 60 . 3 Câu 20: Biết 2
lim ( 4x − 2x − ax − b) =
. Giá trị b nằm trong khoảng nào sau đây? x→+∞ 4  1 4   5 3   5 7   3 3  A. ;   − −     − −    3 3 . B. ;   2 2 . C. ;   2 2 . D. ;   2 4 .  Mã đề 123-Trang 2/3
PHẦN 2: TỰ LUẬN (Thời gian làm bài: 30 phút) (5,0 điểm)
Câu 21.(1,5đ) Tính các giới hạn sau: 3 3n − 2n +1 a) lim . b) + − − . →+∞ ( 2 lim 9x x 9 3x x ) 2 2n − 3
Câu 22. (1,0đ) Cho ba cấp số nhân lùi vô hạn (u , (v ) và (w ) với 2 v = u , 3 w = u . n ) n n n n n n 147
Biết tổng của (u , (v ) lần lượt là 7 và
. Tìm tổng của (w ) . n ) n 2 16 n u  = 3 1
Câu 23. (0,5đ) Cho dãy số (un ) xác định bởi  u 2 = + 1 ∀ ≥  1. +1 u , n n n Tính S = 2021 u + 1 u + 2 u +...+ 3 u2021
Câu 24. (2,0đ) Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O và SA ⊥ ( ABCD) .
a) Chứng minh: BD ⊥ (SAC) .
b) Gọi AH là đường cao của S
∆ AB . Chứng minh rằng AH ⊥ BC .
c) Xác định giao điểm K của SC với mặt phẳng ( ADH ) . Chứng minh rằng tứ giác ADKH là hình thang vuông.
------ HẾT ------ Mã đề 123-Trang 3/3
TRƯỜNG THPT PHAN ĐÌNH PHÙNG
ĐỀ KIỂM TRA GIỮA HỌC KÌ II, NĂM HỌC 2020-2021 TỔ TOÁN - TIN Môn: Toán - Lớp 11
Thời gian làm bài : 60 phút
Phần đáp án câu trắc nghiệm (5,0 điểm) 123 246 357 479 1 C D D D 2 C C B D 3 A B B D 4 A B A C 5 D D D B 6 B D B A 7 B C D A 8 B A A D 9 D C A C 10 D C B C 11 D D A B 12 B B C C 13 A A B D 14 D A A C 15 C B B B 16 D B D A 17 D A D C 18 A A A A 19 D B D D 20 D D C A
PHẦN 2: TỰ LUẬN (Thời gian làm bài: 30 phút) (5,0 điểm)
HƯỚNG DẪN CHẤM PHẦN TỰ LUẬN CÂU ĐÁP ÁN ĐIỂM
21(1,5 đ) Tính các giới hạn sau 2 1 − + 3 3 2 3 3n − 2n +1 0,25
a)(1,0đ) L = lim = lim n n . 2 2n − 3 2 3 − 3 n n  2 1  Ta có : lim 3 − + = 3 > 0   (1) 2 3  n n  0,25  2 3  2 3 và lim − = 0, − > 0, n ∀ ∈ (n ≥ 2)   (2) 3 3  n n  n n 0,25 L = +∞ (3) 0,25
Ghi chú: Nếu Hs thiếu hai bước (1) , (2) mà suy ra bước (3) thì trừ 0,25đ 2 2
 9x + x − 9 − 9x  b) (0,5đ) + − − = lim   0,25 →+∞ ( 2 lim 9x x 9 3x x ) x→+∞ 2
 9x + x − 9 + 3x  9 1− x − 9 1 = lim = lim x = . x→+∞  0,25 1 9 x→+∞  1 9 6 x  9 + − + 3 9 + − + 3 2 2 x x x x   1 22(1,0đ)
Cho ba cấp số nhân lùi vô hạn (u , (v ) và (w ) với 2 v = u , 3 w = u . n ) n n n n n n 147
Biết tổng của (u , (v ) lần lượt là 7 và
. Tìm tổng của (w ) . n ) n 2 16 n CÂU ĐÁP ÁN ĐIỂM Giả sử 7 147 S = , S =
, S là tổng của (w . n ) 1 2 2 16 3 u 7 Ta có 1 S =
= ⇒ 2u + 7q = 7 (1). 1 1 0,25 1− q 2 2 u 147 u u 147 7 u 147 1 1 1 1 S = = ⇔ . = ⇔ . =
⇔ 8u − 21q = 21 (2) 2 0,25 2 1 1− q 16 1− q 1+ q 16 2 1+ q 16 22(1,0đ) u  = 3 1
Giải hệ phương trình (1) và (2) ta được  0,25 1 q =  7 3 3 Do đó u 3 1029 1 S = = = . 3 0,25 3 1− q 1 38 1− 3 7 u  = 3 1
Cho dãy số (un ) xác định bởi  u 2 = + 1 ∀ ≥  1. +1 u , n n n Tính S = 2021 u + 1 u + 2 u +...+ 3 u2021
Xét dãy số (v với v = u – 1 , n ≥ 1. n ) n n Ta có v = u − 1 1 1 = u + − 1 1 = (u − 1 1) =
v ,với mọi n ≥ 1. n 1 + n 1 + 2 n 2 2 n 2 n Khi đó dãy số 1
(v là một CSN lùi vô hạn với v = 2 , công bội q = . n ) 1 2 0,25 23(0,5đ) n−2 Do đó  1  v = . n    2  n−2  1 
Suy ra u = v +1 =
+1 ,với mọi n ≥1. n n    2  − − n k 2 n  n 2 1   1 
Mà S = ∑u = ∑ + n = 4 + n − . n k        2  k = 2 k 1 = 1 0,25 2021−2  2019 1   1  Vậy S = 4 + 2021− = 2025 − . 2021      2   2 
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O và SA ⊥ ( ABCD) . 24(2,0đ)
a) Chứng minh: BD ⊥ (SAC) .
b) Gọi AH là đường cao của S
∆ AB . Chứng minh rằng AH ⊥ BC .
c) Xác định giao điểm K của SC với mặt phẳng ( ADH ) . Chứng minh rằng tứ
giác ADKH là hình thang vuông. 2 0,25
Vẽ được hình chóp  D B ⊥ AC  a)(1,0đ) Ta có:  0,5  D B ⊥ SA 
(vi SA ⊥ (ABCD)) ⇒ D B ⊥ (SAC) 0,25 BC ⊥ SA  b) (0,5đ) Ta có:
 ⇒ BC ⊥ (SAB) . 0,25 BC ⊥ AB
Mặt khác: AH ⊂ (SAB) ⇒ BC ⊥ AH . 0,25
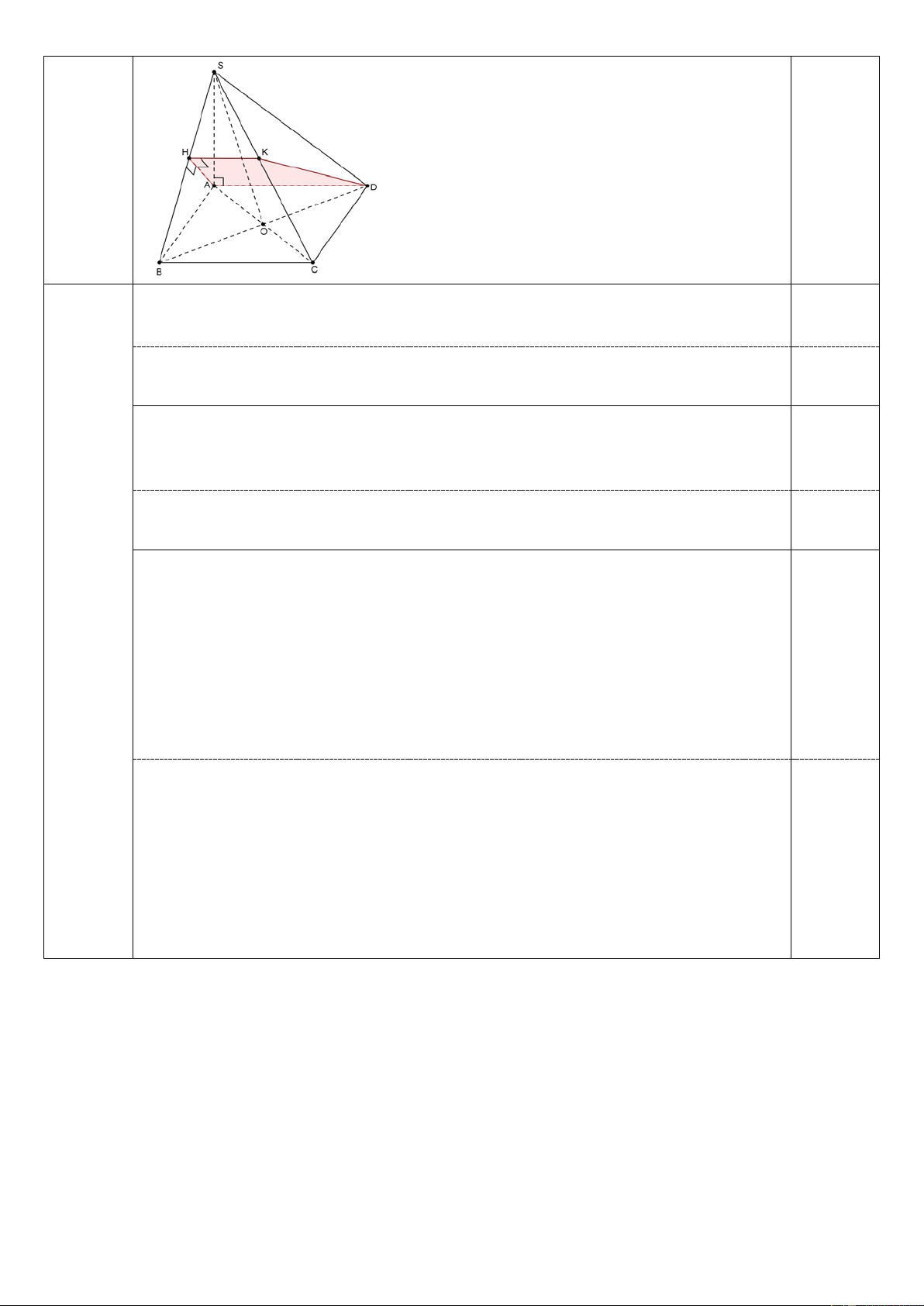
c)(0,5đ) Xác định giao điểm K của SC với mặt phẳng ( ADH ) :
H ∈ ( AHD) ∩ (SBC)  AD / / BC 
 ⇒ (AHD) ∩ (SBC) = H ;
x Hx / / AD / / BC . AD ⊂ ( AHD)  0,25 BC ⊂ (SBC) 
⇒ K = Hx ∩ SC . Suy ra ADKH là hình thang.
*) Chứng minh ADKH là hình thang vuông: Ta có:
AD ⊥ SA (SA ⊥ ( ABCDH ) ⊃ AD)   ⇒
 AD ⊥ (SAB)
AD ⊥ AB ( ABCD là hình vuông)  
 ⇒ AD ⊥ AH 0,25  AH ⊂ (SAB) 
⇒ ADKH là hình thang vuông tại A và H.
Ghi chú: Học sinh làm cách khác đúng vẫn cho đủ điểm từng phần như trong đáp án. 3
Document Outline

• de 123
• Huong dan cham G Ki II Toan 11(đã sửa lại )