Đề thi HK1 Toán 11 năm 2019 – 2020 trường THPT An Dương Vương – TP HCM

SỞ GIÁO DỤC VÀ ĐÀO TẠO TP HỒ CHÍ MINH KIỂM TRA HỌC KÌ 1
TRƯỜNG THPT AN DƯƠNG VƯƠNG Môn: Toán - Khối: 11 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút (Đề thi có 01 trang)
Họ và tên thí sinh: ............................................................................. ; Lớp:................................................
Câu 1 (1 điểm). Tính tổng các nghiệm của phương trình sin x  3 cos x  2 trên 0;4 . Câu 2 (2 điểm).
a) Cho cấp số cộng u có công sai d  2 . Tổng tám số hạng đầu là S  72 . Tìm 5 số hạng đầu của n  8 cấp số trên. v  243v 3 8 
b) Cho cấp số nhân v biết
. Tìm số hạng tổng quát của v . n  n   2 v   4  27
Câu 3 (0.75 điểm). Một hộp chứa 5 quả cầu đen và 4 quả cầu trắng (tất cả các quả cầu đều khác nhau).
Lấy ngẫu nhiên đồng thời 3 quả. Tính xác suất để được 3 quả có đủ hai màu.
Câu 4 (1 điểm). Hai đường thẳng a và b cắt nhau tại điểm O . Trên đường thẳng a , lấy 8 điểm khác
nhau (không tính điểm O ). Trên đường thẳng b , lấy 10 điểm khác nhau (không tính điểm O ). Tính số
tam giác có 3 đỉnh được lấy từ 19 điểm bao gồm 18 điểm ở trên và điểm O . 8  x 
Câu 5 (0.75 điểm). Tìm hệ số của số hạng chứa 3
x trong khai triển P  x  2  5x 1   .  2  t   2
Câu 6 (0.5 điểm). Cho dãy số t được xác định bởi 1 . Chứng minh n  t  2t 3, n  2  n n 1  n 1  * t  5.2
 3, n   bằng phương pháp quy nạp. n
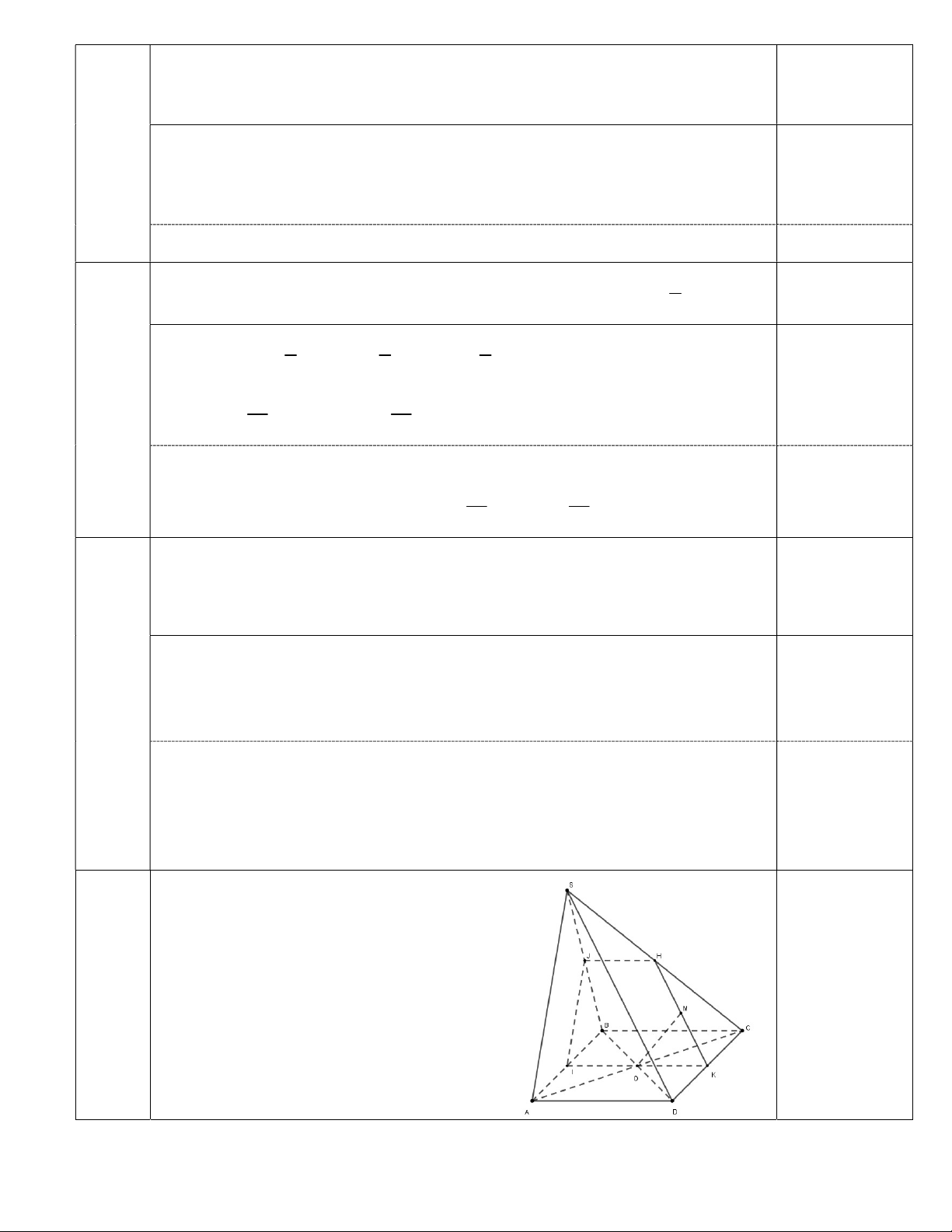
Câu 7 (2.5 điểm). Cho hình chóp S.ABCD đáy ABCD là hình bình hành tâm O . Gọi H , K, M lần
lượt là trung điểm SC,CD và HK .
a) Tìm giao tuyến của hai mặt phẳng SAB và SCD .Từ đó tìm giao điểm của DH và SAB .
b) Tìm thiết diện của OHK  với hình chóp S.ABCD .
c) Chứng minh MO song song SAD .
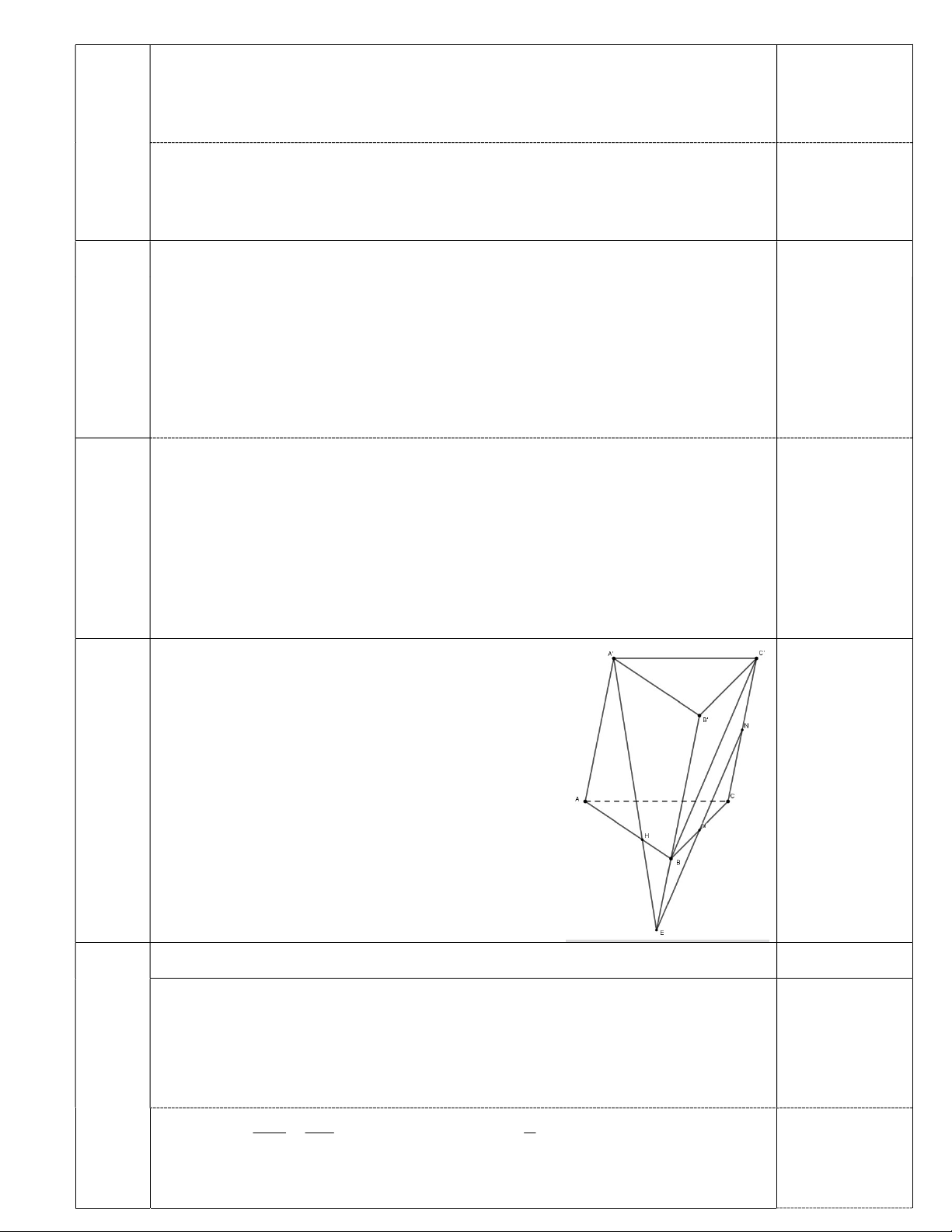
Câu 8 (1 điểm). Cho lăng trụ ABC.A' B 'C ' . Gọi M , N lần lượt là trung điểm của BC và CC '.
a) Chứng minh MN song song  A' BC ' .
b) Mặt phẳng  A'MN  cắt AB tại H . Tính tỉ số AH : AB .
Câu 9 (0.5 điểm). Cho ba số thực dương a,b, c là ba số hạng liên tiếp của một cấp số nhân đồng thời 2 2 2 a b c 1 1 1 thỏa mãn điều kiện
 4 . Tính giá trị của biểu thức P    . 3 3 3 a  b  c 3 3 3 a b c --- HẾT---
Học sinh không được sử dụng tài liệu. Cán bộ coi thi không được giải thích gì thêm.
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP HỒ CHÍ MINH
ĐÁP ÁN VÀ THANG ĐIỂM KÌ THI
TRƯỜNG THPT AN DƯƠNG VƯƠNG KIỂM TRA HỌC KÌ I Môn: Toán - Khối: 11 Câu Đáp án Điểm Câu 1
Tính tổng các nghiệm của phương trình sin x  3 cos x  2 trên 0;4 . 1đ 1 3   
sin x  3 cos x  2  sin x  cos x  1  sin x  1   2 2  3  0.25    0.25
 x    k2  x   k2 k  3 2 6    0.25
Theo đề bài ta có: x    1 23 13 0; 4   k   k  0,1 x  , 12 12 6 6 7 0.25 Tổng các nghiệm là: 3
Câu 2a a) Cho cấp số cộng u có công sai d  2 . Tổng tám số hạng đầu là S  72 . n  8 1 đ Tìm số hạng đầu u . 1 8u  u 8  u  28d  72 1 8  S   8u  28d . Suy ra: 1   u  16 8 1 2 1 0.25+0.5 d  2 
u  16,u 14,u  12,u 10,u  8 0.25 1 2 3 4 5 Câu 2b v  243v 3 8 1đ 
Cho cấp số nhân v biết
. Tìm số hạng tổng quát của v . n  n   2 v   4  27
Gọi q là công bội của CSN cần tìm. 0.25 x 3  1 2 7 5 v  243v v .q  243v .q q   1 3 8 1 1     243 q   2     (do v .q  0) 2   3 1 3 v  v .q  2 3  4  1  27 v .q   v  2  27 1  1  27 n 1  0.25 n  1  Số hạng tổng quát: 1 v  v .q  2. n 1    3 
Lưu ý: HS không gọi công bội thì không trừ điểm. HS không nói v .q khác 0 trừ 0.125. 1 Câu 3
Một hộp chứa 5 quả cầu đen và 4 quả cầu trắng (tất cả đều có khác nhau). Lấy 0.75đ
ngẫu nhiên đồng thời 3 quả. Tính xác suất để được 3 quả đủ hai màu.
Lây ngẫu nhiên hai quả có 3 C cách. n  3  C 0.25 9 9
Gọi A: “Lấy được 3 quả cầu có đủ hai màu”. Chọn 3 quả cầu đen: 3
C ; Chọn 3 quả cầu trắng: 3 C ; 0.25 5 4 Suy ra: n  A 3 3 3  C  C  C  70 9 5 4 0.25 Vậy P  A 5  6 Câu 4
Hai đường thẳng a và b cắt nhau tại điểm O . Trên đường thẳng a , lấy 8 điểm 1đ
khác nhau (không tính điểm O ). Trên đường thẳng b , lấy 10 điểm khác nhau
(không tính điểm O ) Tính số tam giác có 3 đỉnh được lấy từ 19 điểm bao gồm 18
điểm ở trên và điểm O .
TH1: 1 điểm là O, 1 điểm bất kì trên a và 1 điểm bất kì trên b (khác O) có 1 1 C .C 0.25 x 3 8 10
TH2: 2 điểm trên a (khác O) và 1 điểm trên b (khác O) có 2 1 C .C 8 10
TH3: 2 điểm trên b (khác O) và 1 điểm trên a (khác O) có 2 1 C .C 10 8
Số tam giác được tạo thành: 1 1 2 1 2 1
C .C  C .C  C .C  720 0.25 8 10 8 10 10 8 Câu 5 8  x  0.75đ
Tìm hệ số của số hạng chứa 3
x trong khai triển P  x  2  5x 1   .  2  8 8 8 0.25    x   x   x  P 2  5x 1  2. 1  5 . x 1        2   2   2  8 k 8  1    1 i  k k i  i 1  2.C . .x 5.C . .x  8   8   k 0  2  i0  2  0.25
Theo đề bài, ta có k  3,i  2 . 3 2 0.25  1  1
Vậy hệ số của số hạng chứa 3 x là 3 2 2.C .  5.C .  21. 8   8    2   2  Câu 5b t   2 0.5đ
Cho dãy số t được xác định bởi 1 . Chứng minh n  t  2t 3, n  2  n n 1  n 1  * t  5.2
 3,n  bằng phương pháp quy nạp. n n 1  * t  5.2  3,n  (*) 0.25 n Với 1 1 n 1,t 5.2     3  2 1
Giả sử (*) đúng với   *
n k k    , tức là ta có k 1 t 5.2    3. k
Ta cần chứng minh (*) đúng với n  k 1 , nghĩa là chứng minh t  5.2k  3. 0.25 k 1  Thật vậy t  2t  3  2.      . k  k  k 1 5.2 3 3 5.2k 3 1 
Suy ra (*) đúng với n  k 1 . Vậy (*) đúng với mọi * n 
Câu 6a Cho hình chóp S.ABCD đáy ABCD là 1.0đ
hình bình hành tâm O . Gọi H , K, M lần
lượt là trung điểm SC,CD và HK .
a) Tìm giao tuyến của hai mặt phẳng SAB
và SCD .Từ đó tìm giao điểm của DH và SAB. S SAB SCD  0.5  AB  CD
  SAB SCD  Sx / / AB / /CD AB SAB,CD SCD   
Trong SCD, DH Sx  E 0.5 E  DH     E  DH  (SAB) E  Sx  (SAB)
Câu 6b b) Tìm thiết diện của OHK  với hình chóp S.ABCD . 1.0đ Xác định được
Trong  ABCD,OK  AB  I mỗi giao tuyến (kể cả bước kẻ
Từ H kẻ đường thẳng song song BC (// OK) cắt SB tại J;  HJ  OHK  thêm) được 0.25
OHKSCD  HK;OHK ABCD  KI 
OHK   SAB  IJ;OHK  SBC   HJ
Vậy thiết diện của (OHK) với hình chóp S.ABCD là tứ giác HKIJ.
c) Chứng minh MO song song SAD . OK  AD   0.25 OH  SA DoOH là dtb S  AC     Trong OHK  OHK  SCD ,OH  OK  O  Trong SAD, SA AD A    
Mà OM  OHK   OM  SAD 0.25
Câu 7a Cho lăng trụ ABC.A' B 'C ' . Gọi M , N lần lượt là 1.0đ
trung điểm của BC và CC '.
a) Chứng minh MN song song  A' BC ' . M là trung điểm CB N trung điểm CC’  MN  BC ' 0.25 MN   A'BC ' MN  BC '   MN   A' BC ' 0.25 BC '  A'BC '  
Câu 7b b) Mặt phẳng  A'MN  cắt AB tại H . Tính tỉ số AH : AB . 1.0đ
Trong BCC ' B ', MN  BB '  E 0.25
Trong  ABB ' A', A' E  AB  H H  AB    H  AB  A MN H  A' E   A'MN   '   CM CN 1 0.25 CN  BE  
 1 CN  BE  BE  BB ' BM BE 2 AH AA' AH 2 BE  AA'    2   HB BE AB 3 Câu 9
Cho ba số thực dương a,b, c là ba số hạng liên tiếp của một CSN đồng thời thỏa 2 2 2 a b c 1 1 1 mãn điều kiện
 4 . Tính giá trị của biểu thức P    ? 3 3 3 a  b  c 3 3 3 a b c 2 2 2 3 3 3 a b c 1 a  b  c a b c 0.25 Ta có  4      . 3 3 3 2 2 2 2 2 2 2 2 2 a  b  c 4 a b c b c c a a b
Mặt khác vì a,b, c là ba số hạng liên tiếp của một cấp số nhân nên 2 ac  b . 1 a b c a b c 1 1 1 1 0.25 Do vậy:           P  . 2 2 2 2 2 2 3 4 3 3 3 3 4 b c c a a b ac b a c a b c 4
Lưu ý: Học sinh làm cách khác đúng được trọn điểm.