Đề thi HK1 Toán 11 năm 2019 – 2020 trường THPT Mạc Đĩnh Chi – TP HCM

SỞ GIÁO DỤC & ĐÀO TẠO TP. HCM
TRƯỜNG THPT MẠC ĐĨNH CHI
ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2019 – 2020
MÔN TOÁN – KHỐI LỚP 11 (11A2  11A24)
Thời gian làm bài: 90 phút
Bài 1(1điểm). Lập bảng biến thiên của hàm số y  sin x trên đoạn    ;  .
Bài 2(1.5điểm). Giải các phương trình: a. sin 2x   1 2cos x  3  0 . 4 4
cos x  sin x  3 sin 2x  2 b.  0 . 2cos x 1
Bài 3(1điểm). Có bao nhiêu số tự nhiên chia hết cho 5 và có 3 chữ số khác nhau?
Bài 4(1điểm). Trong khai triển của biểu thức P  x  y 15 2 2
, hãy tìm hệ số của 12 6 x y .
Bài 5(1điểm). Trên một đường tròn cho n điểm phân biệt. Biết số tam giác có 3 đỉnh lấy từ n điểm này
nhiều hơn số đoạn thẳng có 2 đầu mút cũng được lấy từ n điểm này là 75. Tìm n. Bài 6(1 điểm).
a. Xác suất ném bóng vào rổ thành công trong mỗi lần ném của bốn học sinh An, Bảo, Cường,
Danh lần lượt là 0.5, 0.6, 0.7, 0.8. Cho mỗi học sinh trên ném bóng vào rổ 1 lần. Tính xác suất có ít nhất
một người ném thành công.
b. Trong kỳ thi học kỳ 1, phòng thi số 1 có 24 học sinh trong đó có 4 học sinh tên An, Bảo,
Cường, Danh. Trong phòng thi có 24 bàn xếp thành 4 dãy theo hàng dọc, mỗi dãy có 6 bàn. Giám thị
phòng thi bố trí cho các học sinh ngồi ngẫu nhiên vào 24 bàn, mỗi bàn 1 học sinh. Tính xác suất 4 bạn có
tên trên ngồi cạnh nhau theo cùng một hàng dọc.
Bài 7(3.5điểm). Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Điểm E thuộc cạnh SC 1 thỏa CE  SC . 3
a. Tìm giao điểm F của đường thẳng BE và mặt phẳng (SAD).
b. Gọi G  SD  AF . Chứng minh EG // AB // CD .
c. Gọi H là trọng tâm tam giác ACD. Chứng minh: HE //(SAB) .
d. Gọi I  AD  (HEG) , K  BC  (HEG) , M  KE  IG và điểm N thuộc cạnh SB sao cho
SB  3SN . Chứng minh MN //(ABG) .
SỞ GIÁO DỤC & ĐÀO TẠO TP. HCM
TRƯỜNG THPT MẠC ĐĨNH CHI
ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2019 – 2020
MÔN TOÁN – KHỐI LỚP 11 (11A2  11A24)
Thời gian làm bài: 90 phút
Bài 1(1điểm). Lập bảng biến thiên của hàm số y  sin x trên đoạn    ;  .
Bài 2(1.5điểm). Giải các phương trình: a. sin 2x   1 2cos x  3  0 . 4 4
cos x  sin x  3 sin 2x  2 b.  0 . 2cos x 1
Bài 3(1điểm). Có bao nhiêu số tự nhiên chia hết cho 5 và có 3 chữ số khác nhau?
Bài 4(1điểm). Trong khai triển của biểu thức P  x  y 15 2 2
, hãy tìm hệ số của 12 6 x y .
Bài 5(1điểm). Trên một đường tròn cho n điểm phân biệt. Biết số tam giác có 3 đỉnh lấy từ n điểm này
nhiều hơn số đoạn thẳng có 2 đầu mút cũng được lấy từ n điểm này là 75. Tìm n. Bài 6(1 điểm).
a. Xác suất ném bóng vào rổ thành công trong mỗi lần ném của bốn học sinh An, Bảo, Cường,
Danh lần lượt là 0.5, 0.6, 0.7, 0.8. Cho mỗi học sinh trên ném bóng vào rổ 1 lần. Tính xác suất có ít nhất
một người ném thành công.
b. Trong kỳ thi học kỳ 1, phòng thi số 1 có 24 học sinh trong đó có 4 học sinh tên An, Bảo,
Cường, Danh. Trong phòng thi có 24 bàn xếp thành 4 dãy theo hàng dọc, mỗi dãy có 6 bàn. Giám thị
phòng thi bố trí cho các học sinh ngồi ngẫu nhiên vào 24 bàn, mỗi bàn 1 học sinh. Tính xác suất 4 bạn có
tên trên ngồi cạnh nhau theo cùng một hàng dọc.
Bài 7(3.5điểm). Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Điểm E thuộc cạnh SC 1 thỏa CE  SC . 3
a. Tìm giao điểm F của đường thẳng BE và mặt phẳng (SAD).
b. Gọi G  SD  AF . Chứng minh EG // AB // CD .
c. Gọi H là trọng tâm tam giác ACD. Chứng minh: HE //(SAB) .
d. Gọi I  AD  (HEG) , K  BC  (HEG) , M  KE  IG và điểm N thuộc cạnh SB sao cho
SB  3SN . Chứng minh MN //(ABG) .
ĐÁP ÁN KIỂM TRA HỌC KỲ I – NĂM HỌC 2019 – 2020
MÔN TOÁN – KHỐI LỚP 11 Bài 1
Lập bảng biến thiên của hàm số y  sin x trên đoạn    ; . (1đ) x       2 2 y 0 1 0.75 -1 0
Có tính giá trị của y trong BBT. 0.25 Bài 2a
Giải phương trình: sin 2x   1 2cos x  3  0 . (1đ) sin 2x 1 pt   3  0.25 cos x   2  sin 2x  1  x   k 0.25 4 3   0.25+0.25 cos x 
 cos  x    k2 2 6 6 Bài 2b 4 4
cos x  sin x  3 sin 2x  2 Giải phương trình:  0 . (0.5đ) 2cos x 1  ĐK: x    k2 3 4 4
pt  cos x  sin x  3 sin 2x  2  0
 cos2x  3 sin 2x  2     sin 2x   1     6     x   k 0.25 3 2 0.25
So đk ta nhận nghiệm x   k2 . 3 Bài 3
Có bao nhiêu số tự nhiên chia hết cho 5 và có 3 chữ số khác nhau? (1đ) Gọi n  abc (a  0)
TH1: c = 0: a, b lần lượt có 9, 8 cách chọn. 0.25 Suy ra có 9.8 = 72 số. 0.25
TH2: c = 5: a, b lần lượt có 8, 8 cách chọn. Suy ra có 8.8 = 64 số. 0.25 Vậy có 72 + 64 = 136 số. 0.25
Lưu ý HS chỉ đúng 1 TH cho 0.5đ, chỉ đúng 2 TH cho 0.75đ, đúng đáp số cho 1 Bài 4
Trong khai triển của biểu thức P  x  y 15 2 2
, hãy tìm hệ số của 12 6 x y . (1đ) 15 15 k Ta có: k 15k P  C x  2 2y  k k 15k 2  C ( 2  ) k x y 15 15 0.25+0.25 k 0 k 0 1  5  k 12 0.25 Cho   k  3 2k  6 Hệ số của 12 6 x y là 3 3 C (2)  3640 . 0.25 15 Bài 5
Trên một đường tròn cho n điểm phân biệt. Biết số tam giác có 3 đỉnh lấy (1đ)
từ n điểm này nhiều hơn số đoạn thẳng có 2 đầu mút cũng được lấy từ n điểm này là 75. Tìm n. Số tam giác là 3 C n 0.25 Số đoạn thẳng 2 C 0.25 n Ta có pt: 3 C - 2 C = 75 n n ĐK: n  N,n  3 n! n! PT    75 (n  3)!3! (n  2)!2! 0.25 n(n 1)(n  2) n(n 1)    75 6 2 0.25 3 2
 n  6n  5n  450  0  n  10 (nhận). Bài 6a
a. Xác suất ném bóng vào rổ thành công trong mỗi lần ném của bốn học (0.5đ)
sinh An, Bảo, Cường, Danh lần lượt là 0.5, 0.6, 0.7, 0.8. Cho mỗi học sinh
trên ném bóng vào rổ 1 lần. Tính xác suất có ít nhất một người ném thành công.
- Xác suất cả 4 bạn ném không thành công là
0.5 x 0.4 x 0.3 x 0.2 = 0.012 0.25
- Xác suất có ít nhất 1 người ném thành công là 1- 0.012 = 0.988 0.25 Bài 6b
b. Trong kỳ thi học kỳ 1, phòng thi số 1 có 24 học sinh trong đó có 4 (0.5đ)
học sinh tên An, Bảo, Cường, Danh. Trong phòng thi có 24 bàn xếp thành
4 dãy theo hàng dọc, mỗi dãy có 6 bàn. Giám thị phòng thi bố trí cho các
học sinh ngồi ngẫu nhiên vào 24 bàn, mỗi bàn 1 học sinh. Tính xác suất 4
bạn có tên trên ngồi cạnh nhau theo cùng một hàng dọc.   24!
Gọi A là biến cố 4 bạn An, Bảo, Cường, Danh ngồi cạnh nhau theo cùng một hàng dọc.
Chọn ra 1 dãy, chọn ra 4 bàn cạnh nhau của dãy vừa chọn, xếp 4 học sinh vào,
xếp 20 học sinh còn lại. Ta được:   4.3.4!.20! 0.25 A 4.3.4!.20! 2  P( ) A   . 0.25 24! 1771 Bài 7
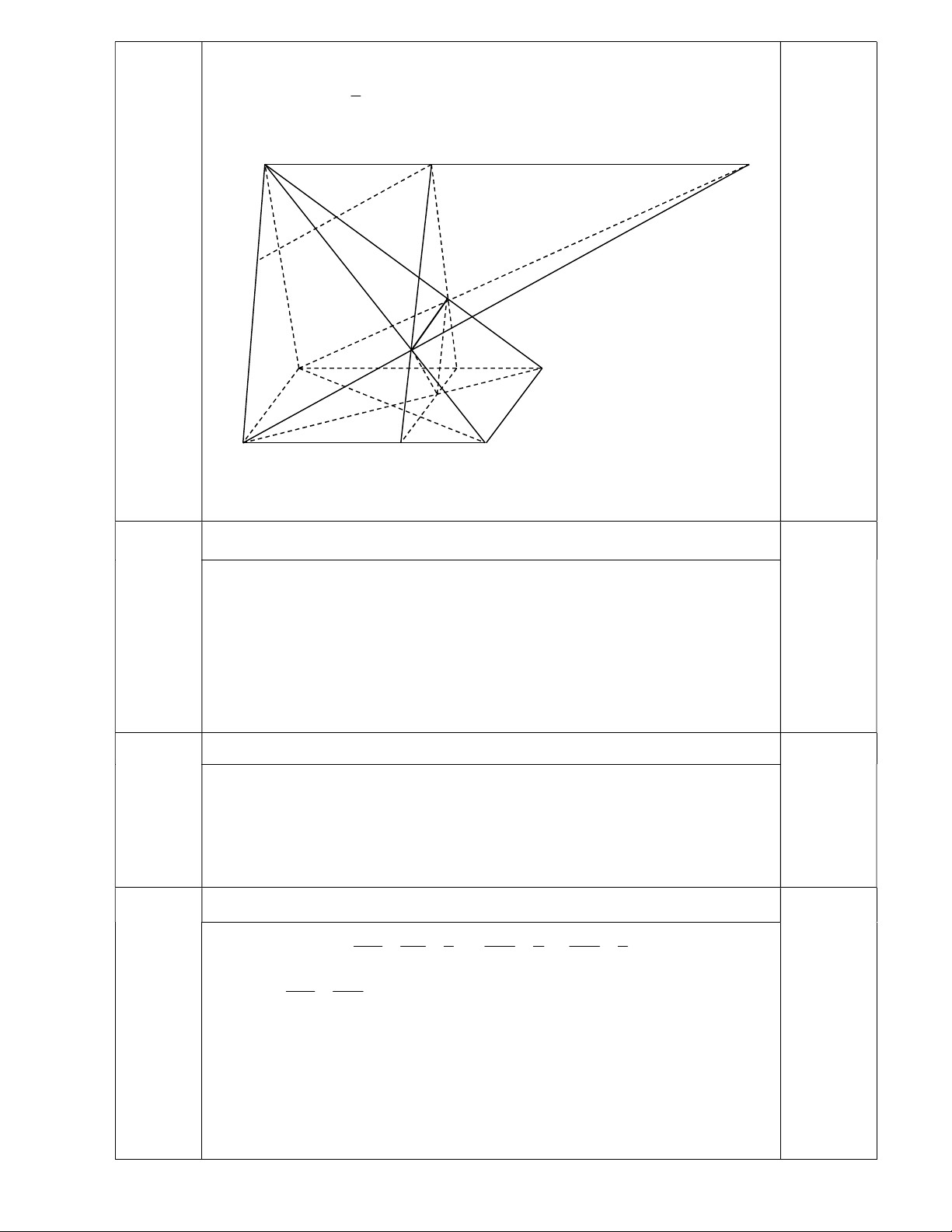
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Điểm E thuộc 1 cạnh SC thỏa CE  SC . 3 S M F N G E I A D O H B C K Bài 7a
a. Tìm giao điểm F của đường thẳng BE và mặt phẳng (SAD). (1đ)
- Chọn mp chứa BE là (SBC) S (SBC),S (SAD) 0.25  0.25 BC // AD BC  (SBC), AD  (SAD) 
 (SBC)  (SAD)  Sx // BC // AD 0.25 0.25
- Gọi F  BE  Sx  F  BE  (SAD) - Bài 7b
b. Gọi G  SD  AF . Chứng minh EG // AB // CD . (1đ) (SCD)  (FAB)  EG 0.5 C  D // AB 0.25 -  CD  (SCD), AB  (FAB)   EG // AB // CD 0.25 Bài 7c
c. Gọi H là trọng tâm tam giác ACD. Chứng minh: HE //(SAB) . (0.75đ) DG CE 1 DH 2 DH 1 - EG // CD    và    DS CS 3 DO 3 DB 3 DG DH 0.25    GH // SB DS DB G  E // A ; B GH // SB  - G  E GH  G  (HEG) //(SAB) 0.25 G
 E,GH  (HEG); AB,SB  (SAB)  0.25
- Do HE  (HEG)  HE //(SAB) . Bài 7d
d. Gọi I  AD  (HEG) , K  BC  (HEG) , M  KE  IG và điểm N thuộc (0.75đ)
cạnh SB sao cho SB  3SN . Chứng minh MN //(ABG) .
- Do EG // CD  (HEG)  (ABCD)  Hy // CD // EG .  I  Hy  A ; D K  Hy  BC (SBC)  (SAD)  SF 0.25   M  SF M (SBC),M (SAD) SM ES CK DH 1 SM 2 -   2 và   suy ra  CK EC CB DB 3 CB 3 SF ES SM 1 Mà   2   0.25 CB EC SF 3 SN 1 SM SN -     MN // FB  MN //(ABG) SB 3 SF SB 0.25