


Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ I (NĂM HỌC 2019 – 2020) THÀNH PHỐ HỒ CHÍ MINH MÔN: TOÁN – KHỐI 11
TRƯỜNG THPT NGUYỄN TRUNG TRỰC
Thời gian làm bài: 90 phút, không kể thời gian giao đề ĐỀ CHÍNH THỨC
Câu 1. (2,0 điểm) Giải các phương trình lượng giác: a) 2 sin 2x 1 0 4
b) 2cos 2x 5cos x 3 0
Câu 2. (1,0 điểm) Giải phương trình 2 3.C 2 2.A 1 C . n n1 n1 10
Câu 3. (1,0 điểm) Tìm số hạng không chứa x trong khai triển của 3 2 x ( x 0 ). 3 x
Câu 4. (1,0 điểm) Trong một hộp đựng 20 quả nhãn, 15 quả nho, 10 quả sơri. Lấy
ngẫu nhiên ra 3 quả. Tính xác suất để lấy ra được các loại quả khác nhau.
Câu 5. (1,0 điểm) Một người có 10 đôi giày khác nhau. Trong lúc đi du lịch vội vã
nên đã lấy ngẫu nhiên 4 chiếc giày. Tính xác suất để người đó không lấy được đôi giầy nào đúng.
Câu 6. (3,0 điểm) Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M là trung điểm của SD.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Chứng minh OM song song với mặt phẳng (SBC).
c) Tìm giao điểm của BM và mặt phẳng (SAC).
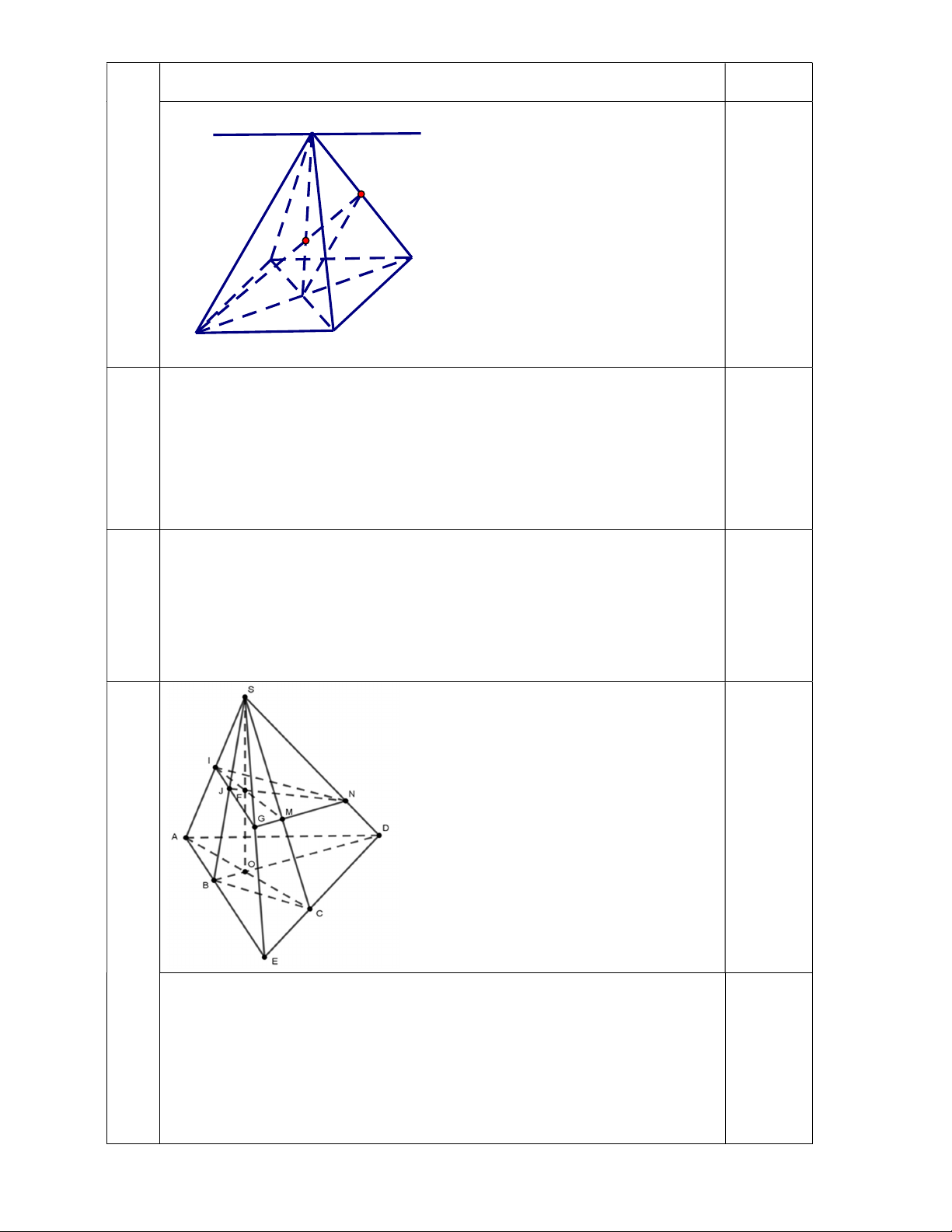
Câu 7. (1,0 điểm) Cho hình chóp S.ABCD có đáy là tứ giác có các cặp cạnh đối
không song song. AB cắt CD tại E. Gọi I, J lần lượt là trung điểm của SA, SB. Lấy N trên
SD sao cho SN=2ND. Lấy M là giao điểm của SC với (IJN). Chứng minh IJ, MN và SE đồng quy. -----HẾT-----
ĐÁP ÁN TOÁN KHỐI 11 KIỂM TRA HKI NĂM HỌC 2019 – 2020 CẤU NỘI DUNG ĐIỂM 1a 2 sin 2x 1 0 4 sin 2x sin 4 4 0.25 2x k2 4 4 0.25
2x k2 4 4 0.25 x k 4 (k Z ) x k 2 0.25 1b
2cos 2x 5cos x 3 0 2
2(2 cos x 1) 5cos x 3 0 0.25 2
4 cos x 5cos x 1 0 cos x 1 0.25 1 cos x 4
cos x 1 x k2 (k Z ) 0.25 1 cos x 1 / 4 x arccos k2 4 0.25 2 2 3.C 2 2.A 1 C (3) n n1 n1 n 3 0.25 Điều kiện: n N n! (n 1)! (n 1)! 0.25 3 3 2 2!(n 2)! (n 3)! n! 3
n(n 1) 2n 1 (n 2) n 1 2 2 n 7n 10 0 0.25 n 5(N) 0.25 Vậy n=5 n 2(L) 3 10
Tìm hệ số tự do trong khai triển của 3 2 x ( x 0 ). 3 x 0.25 k 3 k k Số hạng tổng quát: T C . x k 10 2 . 1 10 3 x k k 205 .(3) . k C x (0 k 10, k N ) 0.25 10
Theo yêu cầu đề bài ta có: 20 5k 0 k 4 0.25
Vậy hệ số tự do là: 17010 0.25 4
Trong một hộp đựng 20 quả nhãn, 15 quả nho, 10 quả sơri. Lấy
ngẫu nhiên ra 3 quả. Tính xác suất để lấy ra được các loại quả khác nhau. 3 n() C 0.25 45
Gọi A là biến cố cần tìm xác suất.
n(A) 20.15.10 3000 0.25 0.5 P A n( ) A 3000 100 3 n() C 473 45 5
Một người có 10 đôi giày khác nhau. Trong lúc đi du lịch vội vã
nên đã lấy ngẫu nhiên 4 chiếc giày. Tính xác suất để người đó
không lấy được đôi giầy nào đúng. 4 n() C 4845 0.25 20
Gọi A là biến cố cần tìm xác suất 4 C 10
Chọn 4 đôi trong 10 đôi giày có: 0.25
Mỗi đôi (trong 4 đôi trên) chọn 1 chiếc giày: 24=16 n(A) 4 4 C .2 3360 10 0.25 0.25 P A n( ) A 3360 224 4 n() C 323 20 6 x S M S SAD SBC 0.25 AD / /BC Ta co ': 0.25 I AD (SAD) D A BC (SBC) 0.25 O
SAD SBC Sx, Sx / /AD / /BC. B C 0.25 6b
Ta có: M, O lần lượt là trung điểm của SD, BD 0.25
OM là đường trung bình của S BD 0.25 OM / / SB 0.25 Mà SB (SBC) 0.25 OM / /(SBC) 6c Kẻ BM cắt SO tại I 0.25 I BM 0.25 I SO (SAC) 0.25 I BM (SAC) 0.25 7
Chọn mp phụ chứa SC là (SAC). Kẻ AC cắt BD tại O.
Trong (SBD) kẻ NJ cắt SO tại F 0.25 F (INJ ) (SAC) IF (INJ ) (SAC)
Trong (SAC) kẻ IF cắt SC tại M 0.25 M SC (INJ )
Trong (INJ) kẻ IJ cắt MN tại G. G (SAE) (SDE) 0.25 SE (SAE) (SDE) Mà 0.25 G SE dpcm
Học sinh làm cách khác mà ra kết quả đúng vẫn tính điểm




