Đề thi HK1 Toán 11 năm 2019 – 2020 trường THPT Phú Lâm – TP HCM

Nhằm giúp các em học sinh lớp 11 có tư liệu ôn tập để chuẩn bị cho kỳ thi học kì 1 môn Toán 11, sưu tầm và chia sẻ đến các em nội dung đề thi + đáp án + lời giải chi tiết đề thi HK1 Toán 11 năm học 2019 – 2020 trường THPT Phú Lâm, thành phố Hồ Chí Minh.

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 11

Môn: Toán 11

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
Họ và tên học sinh: ……………………………………….- Lớp: ……… – SBD: …………….........
Câu 1. (3.0 điểm) Giải các phương trình lượng giác sau:
a.
2
4sin 2 1 3 sin 3 0;
x x
b.
2 sin 2 cos 3;
x x
c.
2 2
sin 2sin cos 3cos 3 0.
x x x x
Câu 2. (1.0 điểm) Xác định hệ số chứa
5
trong khai triển của nhị thức Newton
10
2019 2020
.
2020 2019
x
Câu 3. (1.5 điểm) Một bình đựng 10 viên bi chỉ khác nhau về màu, gồm 4 bi màu đỏ và 6 bi màu
vàng. Lấy ngẫu nhiên 3 viên bi .Tính xác suất để:
a. Lấy được 1 bi đỏ và 2 bi vàng;
b. Trong ba viên bi lấy được có ít nhất 1 bi màu vàng.
Câu 4. (1.0 điểm) Xác định số hạng đầu
1
u
và công sai
d
của cấp số cộng
n
u
, biết:
1 2 3 4 5 6 7 8 9 10 11
11 1
176
20
u u u u u u u u u u u
u u
Câu 5. (0.5 điểm) Cho cấp số nhân
( )
n
u
có công bội
1
4
q
, số hạng đầu
1
2
u
.Tìm số hạng thứ 2,
thứ 10 của cấp số nhân đó ?
Câu 6. (1.0 điểm) Xác định ảnh của đường tròn
2 2
(C) :( 1) ( 2) 16
x y
qua phép tịnh tiến theo
(2; 3)
u
.
Câu 7. (2.0 điểm) Cho hình chóp .
S ABCD
có đáy
ABCD
là hình bình hành, H là giao điểm của AC và
BD. Gọi
M
là trung điểm của cạnh
,
SA
N
là trung điểm của cạnh SB.
a. Xác định giao tuyến của hai mặt phẳng
( )
SAC
và
( ).
SBD
b. Chứng minh
MN
song song với mặt phẳng
( ).
SCD
--------Hết--------
- Học sinh không sử dụng tài liệu;
- Giám hị coi thi không giải thích gì thêm;
SỞ GIÁO DỤC VÀ ĐÀO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT PHÚ LÂM
ĐỀ KIỂM TRA HỌC KỲ I
NĂM HỌC: 2019-2020
MÔN: TOÁN – LỚP 11
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Đ
Ề CHÍNH THỨC
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ I
NĂM HỌC: 2019 – 2020
MÔN: TOÁN – LỚP 11
Câu Lời giải (cần vắn tắt – rõ các bước được điểm) Điểm
1a
2
4sin 2 1 3 sin 3 0
x x
.
3
sin
2
1
sin
2
x N
x N
sin sin
3
sin sin
6
x
x
2
3
2
2
3
2
6
5
2
6
x k
x k
x k
x k
Vậy họ nghiệm của phương trình
2 5
2 ; 2 ; 2 ; 2
3 3 6 6
S k k k k
0,25
0,25
0,25
0,25
1b
2 sin 2 cos 3
x x
2 2 3
sin cos
2 2 2
x x
sin sin
4 3
x
7
2
12
11
2
12
x k
x k
Vậy họ nghiệm
7 11
2 ; 2 ,
12 12
S k k k
0.25
0.25
0.25
0.25
1c
a.
2 2
sin 2sin cos 3cos 3 0
x x x x
(1)
+ Xét
cos 0
x
suy ra có
cos 0
x
không phải là nghiệm
(1) trở thành:
2
2 tan 2 tan 0
x x
tan tan 0
tan tan
4
x
x
Vậy họ nghiệm của phương trình là
; ;
4
S k k k
0.25
0.25
0.25
0.25
2
10 10
10
10
10
0
2019 2020 2019 2020
2020 2019 2020 2019
k k
k k
k
x C x
Số hạng tổng quát:
10
10
10
2019 2020
2020 2019
k k
k k
C x
Theo yêu cầu đề bài suy ra
5
k
Vậy số hạng chứa
5
10
252
C
0.25
0.25
0.25
0.25
3 Câu 3: (1.5 điểm) Một bình đựng 10 viên bi chỉ khác nhau về màu ,
gồm 4 bi màu đỏ và 6 bi màu vàng. Lấy ngẫu nhiên 3 viên bi .Tính xác
suất để được :
a. “ Ba viên bi lấy được có đúng 1 bi đỏ, 2 bi vàng “.
b. “ Ba viên bi lấy được có ít nhất 1 bi màu vàng “.
Gọi A: “ Ba viên bi lấy được có đúng 1 bi đỏ, 2 bi vàng”
Không gian mẫu:
3
10
n C
Trường hợp thuận lợi của biến cố A:
1 2
4 6
A
n C C
Vậy xác suất của biến cố A:
1 2
4 6
3
10
0,5
C C
P A
C
0.25
0.25
0.25
0.25
3b Gọi B: “ Ba viên bi lấy được có ít nhất 1 bi màu vàng “.
B
: “ Ba viên bi lấy ra không có bi vàng nào“.
Không gian mẫu:
3
10
n C
Trường hợp thuận lợp của biến cố
B
:
3
4
4
B
n C
Vậy xác suất của biến cố B là:
3
4
3
10
29
1 1 0.967
20
C
P B P B
C
0.25
0.25
0.25
0.25
4
11
11 1
176
20
S
u u
1
11 55 176
10 20
u d
d
1
6
2
u
d
0.25
0.25
0.5
5
2 1
1 1
2.
4 2
u u q
9
9
10 1
1 1
2.
4 131072
u u q
0.25
0.25
6
Gọi
u
T I I
và
u
T C C
0.25
Tâm và bán kính của (C) là
1; 2
4
I
R
( '; ')
u
T I I x y
suy ra
3
5
x
y
Vậy
2 2
: 3 5 16
C x y
0.25
0.25
0.25
Câu 7: ( 2 điểm ) Cho hình chóp
.
S ABCD
có đáy
ABCD
là bình hành,
H là giao điểm của AC và BD. Gọi
M
là trung điểm của cạnh
SA
,
N
là
trung điểm của cạnh SB .
a. Xác định giao tuyến của mặt phẳng
( )
SAC
và
( )
SBD
.
b. Chứng minh
MN
song song với mặt phẳng
( )
SCD
.
S là điểm chung thứ nhất
,
H AC BD
H AC SAC H BD SBD
. Suy ra H là điểm chung thứ hai
Vây SH là giao tuyến của
( )
SAC
và
( )
SBD
.
0.25
0.25
0.25
0.25
MN là đường trung bình của tam giác SAB suy ra
/ /
MN AB
Mà
AB/ / CD MN/ / CD
Suy ra
MN/ / SCD
CD SCD
Vậy
MN
song song với mặt phẳng
( )
SCD
0.25
0.25
0.25
0.25
Các cách giải khác (trong phạm vi chương trình học) nếu đúg vẫn được số điểm tối đa
tương ứng.
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO ĐỀ KIỂM TRA HỌC KỲ I THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC: 2019-2020 TRƯỜNG THPT PHÚ LÂM MÔN: TOÁN – LỚP 11
Thời gian làm bài: 90 phút (không kể thời gian phát đề) ĐỀ CHÍNH THỨC
Họ và tên học sinh: ……………………………………….- Lớp: ……… – SBD: …………….........
Câu 1. (3.0 điểm) Giải các phương trình lượng giác sau: a. 2
4sin x  21 3sin x  3  0; b. 2 sin x  2 cos x  3; c. 2 2
sin x  2sin x cos x  3cos x  3  0. 10  2019 2020 
Câu 2. (1.0 điểm) Xác định hệ số chứa 5
x trong khai triển của nhị thức Newton x  .    2020 2019 
Câu 3. (1.5 điểm) Một bình đựng 10 viên bi chỉ khác nhau về màu, gồm 4 bi màu đỏ và 6 bi màu
vàng. Lấy ngẫu nhiên 3 viên bi .Tính xác suất để:
a. Lấy được 1 bi đỏ và 2 bi vàng;
b. Trong ba viên bi lấy được có ít nhất 1 bi màu vàng.
Câu 4. (1.0 điểm) Xác định số hạng đầu u và công sai d của cấp số cộng u , biết: n  1 u
  u  u  u  u  u  u  u  u  u  u  176 1 2 3 4 5 6 7 8 9 10 11  u  u  20  11 1 1
Câu 5. (0.5 điểm) Cho cấp số nhân (u ) có công bội q  , số hạng đầu u  2 .Tìm số hạng thứ 2, n 4 1
thứ 10 của cấp số nhân đó ?
Câu 6. (1.0 điểm) Xác định ảnh của đường tròn 2 2
(C) : (x 1)  ( y  2)  16 qua phép tịnh tiến theo u  (2;3).
Câu 7. (2.0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, H là giao điểm của AC và
BD. Gọi M là trung điểm của cạnh S ,
A N là trung điểm của cạnh SB.
a. Xác định giao tuyến của hai mặt phẳng (SAC) và (SBD).
b. Chứng minh MN song song với mặt phẳng (SCD). --------Hết--------
- Học sinh không sử dụng tài liệu;
- Giám hị coi thi không giải thích gì thêm;
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ I NĂM HỌC: 2019 – 2020 MÔN: TOÁN – LỚP 11 Câu
Lời giải (cần vắn tắt – rõ các bước được điểm) Điểm 2
4sin x  21 3sin x  3  0. 1a  3 sin x  N  2   0,25  1 sin x   N   2   sin x  sin  3   0,25   sin x  sin  6   x   k2  3  2 x   k2  3   0,25   x   k2  6  5 x   k2  6
Vậy họ nghiệm của phương trình  2  5  S    k2;  k2 ;  k2;  k2   3 3 6 6  0,25 2 sin x  2 cos x  3 1b 2 2 3  sin x  cos x  2 2 2 0.25      sin x   sin   0.25  4  3  7 x   k2  12  0.25 11 x   k2  12 7 11  Vậy họ nghiệm S    k2 ;  k2 ,k   12 12  0.25 a. 2 2
sin x  2sin x cos x  3cos x  3  0 (1) 1c 0.25
+ Xét cos x  0 suy ra có cos x  0 không phải là nghiệm (1) trở thành: 2 2 tan x  2 tan x  0 0.25 tan x  tan 0    tan x  tan 0.25  4  
Vậy họ nghiệm của phương trình là 
S  k;  k;k   4  0.25 2 10 10 10  2019 2020   2019 k   2020 k 0.25 k  10k x   C x   10      2020 2019  k 0  2020   2019  10 0.25 k  2019 k   2020 k  Số hạng tổng quát: 10k C x 10      2020   2019 
Theo yêu cầu đề bài suy ra k  5 0.25 Vậy số hạng chứa 5 C  252 10 0.25 3
Câu 3: (1.5 điểm) Một bình đựng 10 viên bi chỉ khác nhau về màu ,
gồm 4 bi màu đỏ và 6 bi màu vàng. Lấy ngẫu nhiên 3 viên bi .Tính xác suất để được :
a. “ Ba viên bi lấy được có đúng 1 bi đỏ, 2 bi vàng “.
b. “ Ba viên bi lấy được có ít nhất 1 bi màu vàng “.
Gọi A: “ Ba viên bi lấy được có đúng 1 bi đỏ, 2 bi vàng” 0.25 Không gian mẫu: 3 n  C  10 0.25
Trường hợp thuận lợi của biến cố A: 1 2 n  C C A 4 6 0.25 1 2 C C
Vậy xác suất của biến cố A: P  A 4 6   0,5 3 C 0.25 10 3b
Gọi B: “ Ba viên bi lấy được có ít nhất 1 bi màu vàng “. 0.25
B : “ Ba viên bi lấy ra không có bi vàng nào“. Không gian mẫu: 3 n  C  0.25 10
Trường hợp thuận lợp của biến cố B : 3 n  C  4 B 4 0.25 C 29
Vậy xác suất của biến cố B là: P B 1 P B 3 4 1   0.967 0.25 3 C 20 10 4 S  176 11  u  u  20  0.25 11 1 1  1u  55d  176 1   1  0d  20 0.25 u   6 1   d  2 0.5 5 1 1 u  u q  2.  2 1 4 2 0.25 9  1  1 9 u  u q  2.  0.25 10 1    4  131072 6
Gọi T I  I và T C  C 0.25 u   u   I 1;2
Tâm và bán kính của (C) là   0.25 R  4 x  3
T I   I (x '; y ') suy ra u  0.25  y  5
Vậy C  x  2   y  2 : 3 5  16 0.25
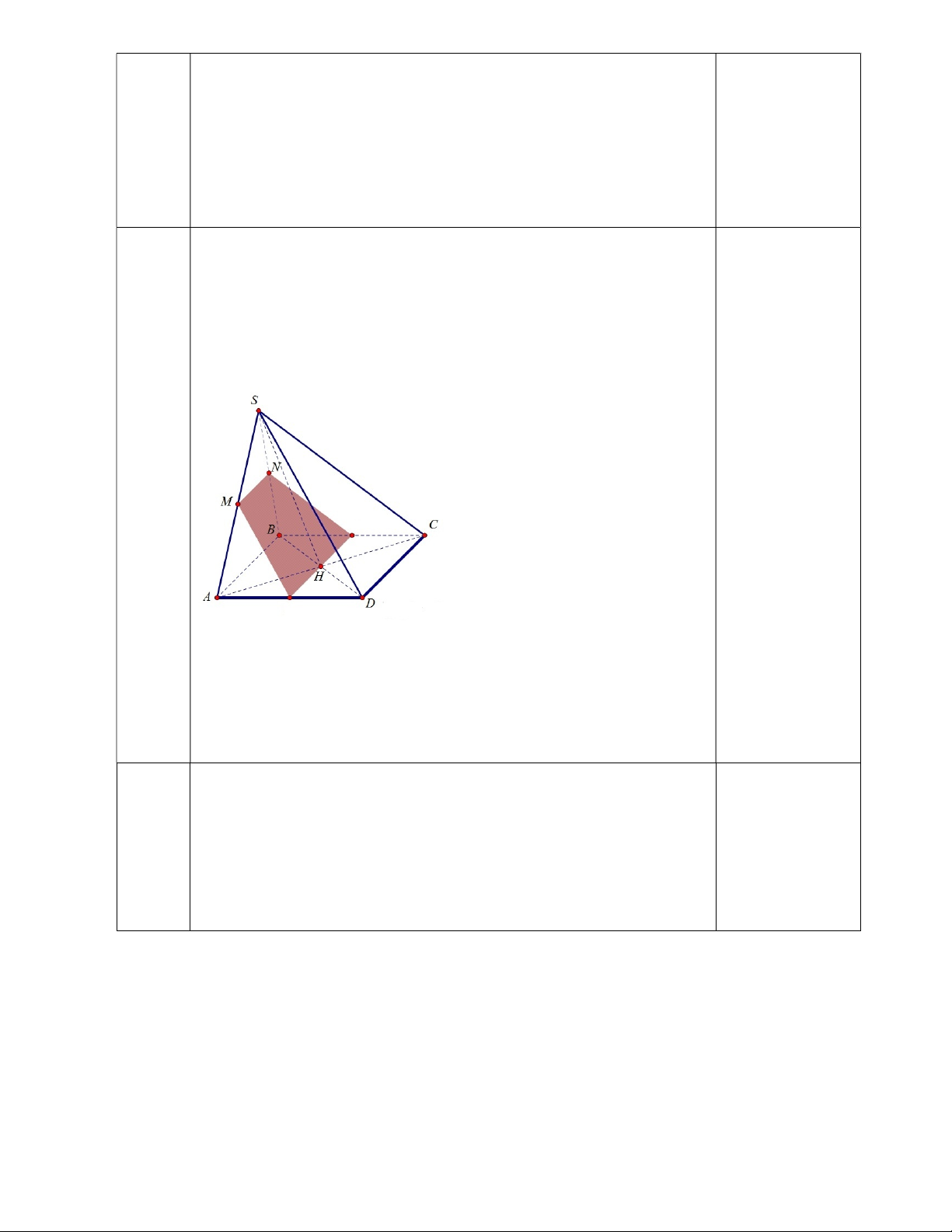
Câu 7: ( 2 điểm ) Cho hình chóp S.ABCD có đáy ABCD là bình hành,
H là giao điểm của AC và BD. Gọi M là trung điểm của cạnh SA , N là
trung điểm của cạnh SB .
a. Xác định giao tuyến của mặt phẳng (SAC) và (SBD) .
b. Chứng minh MN song song với mặt phẳng (SCD) . 0.25
S là điểm chung thứ nhất 0.25 H   AC  BD 0.25 
. Suy ra H là điểm chung thứ hai H  AC  
SAC,H  BD  SBD
Vây SH là giao tuyến của (SAC) và (SBD) . 0.25
MN là đường trung bình của tam giác SAB suy ra MN / / AB 0.25 Mà AB/ / CD  MN/ / CD 0.25 C  D   SCD Suy ra  MN/ / 0.25  SCD
Vậy MN song song với mặt phẳng (SCD) 0.25
Các cách giải khác (trong phạm vi chương trình học) nếu đúg vẫn được số điểm tối đa tương ứng.