




Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2019 – 2020 THÀNH PHỐ HỒ CHÍ MINH Môn : TOÁN – KHỐI 11 TRƯỜNG THPT TÂN PHONG
Thời gian làm bài: 90 phút, không kể thời gian giao đề
Họ và tên HS: ............................................................................... SBD: .....................................
Câu 1/ (2.5 điểm) Giải các phương trình lượng giác sau: a) cos x 3 sin x 2
b) tan(2 x1).tan(3x1) 1 2 c) 6cos x 5cosx1 0 Câu 2/ (1.5 điểm)
a) Từ 6 chữ số 1; 2; 3; 4; 5; 6 có thể lập được bao nhiêu số tự nhiên gồm 3 chữ số đôi một
khác nhau và không chia hết cho 5.
b) Một lớp học có 20 học sinh nam và 19 học sinh nữ. Hỏi có bao nhiêu cách để chọn ra 1
cặp song ca gồm 1 học sinh nam và 1 học sinh nữ? 2 2 12
Câu 3/ (1 điểm) Tìm số hạng không chứa x trong khai triển x ,(x 0) . x Câu 4/ (2 điểm)
a) Từ 9 học sinh gồm 5 nam và 4 nữ. Chọn ngẫu nhiên 6 học sinh xếp thành hàng ngang.
Tính xác suất để không có 2 nam sinh đứng cạnh nhau.
b) Có 7 phiếu bốc thăm, trong đó có 3 phiếu trúng quà. Ông An được phép bốc 3 phiếu.
Tính xác suất để ông An được 2 phiếu trúng quà.
Câu 5/ (1 điểm) Trong mặt phẳng Oxy, cho đường tròn C 2 2
: (x1) ( y 1) 1. Tìm ảnh (C’) của
(C) qua phép vị tự tâm O, tỉ số 2 .
Câu 6/ (2 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi E, F, G lần lượt là trung điểm SA, SB, BC.
a) Chứng minh rằng: EF // (SCD)
b) Tìm giao điểm của AD và mặt phẳng (EFG). HẾT
SỞ GIÁO DỤC – ĐÀO TẠO TP.HCM ĐÁP ÁN ĐỀ KT HỌC KÌ I (Năm học 2019-2020)
TRƯỜNG THPT TÂN PHONG Môn : TOÁN – Lớp 11 – Thời gian : 90 phút Câu Đáp án Điểm
Câu 1a) a) cos x 3sin x 2 1 3 cos x sin x 1 2 2 0.25
cos cos x sin sin x 1 0.25 3 3 cos x cos 0 3 0.25 x k2 3 0.25 x k2(k Z) 3
Câu 1b) b) tan(2x 1).tan(3x 1) 1(*) cos(2x 1) 0 DK : cos(3x1) 0 1 (*) tan(2x 1) cot(3x 1) tan 3x 1 0.25 tan(3x 1) 2
(tan(3x-1)≠0 vì khi tan(3x-1)=0 thay vào phương trình dẫn đến vô lý)
2x 1 3x 1 k 2 k x (k Z ) 0.25 10 5 (thỏa đk) Câu 1c) 2 c) 6cos x 5cosx1 0 (t cosx, 1 t 1) 2 6 t 5t 1 0 0.25 x k2 t 1 cos x 1 0.25+0.5 1 1 1 x arccos k2 (k ) t cos x 6 6 6 1 x arccos k2 6 Câu 2a)
a) Gọi số tự nhiên cần tìm có dạng abc Chọn c : 5 cách 0.25 Chọn a: 5 cách 0.25 Chọn b: 4 cách 0.25 Vậy có 5.5.4=100 số. 0.25
Câu 2b) b) Số cách để chọn ra 1 cặp song ca gồm 1 học sinh nam và 1 học sinh nữ 0.5 1 1 C .C 380 20 19 Câu 3 Số hạng tổng quát: k k 2 12k 2 T C .(x ) . k 1 12 x 0.25 k k 242k 2 C .x . 12 k x 242k x k C .2k 12 k 0.25 x Theo giả thiết ta có: 242k x 0 x k x 24 2k k 0.25 k 8 0.25
Vậy số hạng cần tìm: 8 8 0 C .2 x 126720 12
Câu 4a) a)Số phần tử không gian mẫu 6 n() A 60480 0.25 9 TH1: 3 nam, 3 nữ
Xếp 3 nữ ngồi hàng ngang: 3 A 4 0.25 Chọn ra 3 nam từ 5 nam: 3 C 5 Xếp 3 nam vô 4 chỗ: 3 C 3 A 5 4 Vậy có: 3 A .( 3 C 3 A ) = 5760 cách 4 5 4 TH2: 2 nam, 4 nữ 0.25 Xếp 4 nữ: 4 A 4 Chọn 2 nam từ 5 nam: 2 C 5 Xếp 2 nam vô 5 chỗ: 2 C 2 A 5 5 Vậy có: 4 A .( 2 C 2 A ) = 4800 cách 4 5 5
Vậy xác suất biến cố A: “không có 2 nam sinh đứng cạnh nhau” n( ) A 4800 5760 11 P( ) A n 60480 63 0.25
Câu 4b) b) Số phần tử không gian mẫu 3 n( ) C 35 0.5 7
Số phần tử biến cố A: “ông An được 2 phiếu trúng quà” 2 1 n( ) A C .C 12 0.25 3 4 n( ) A 12 P( ) A n() 35 0.25 Câu 5 Gọi M (x ; y ) (C) M M Ta có: M ' V (M ) (O;2) x M ' x 2 x M x Ta có: M ' M 2 0.25 y 2 y y M ' M M ' y M 2 Vì M (x ; y ) (C) 2 2
(x 1) (y 1) 1 M M M M x y M ' 2 M ' 2 ( 1) ( 1) 1 0.25 2 2 2 2 0.25 (x 2) ( y 2) 4 M ' M ' 0.25 Vậy 2 2
(C ') : (x 2) ( y 2) 4 Câu 6
a) EF/ / AB (vì EF là đường trung bình S AB ) 0.25
Mà AB / /CD ( do ABCD là hình bình hành) 0.25 EF / /CD 0.25 Mà CD (SCD), EF (SCD) 0.25 EF // (SCD) b) AD (ABCD) 0.25 G (ABCD) (EFG) 0.25
EF//CD (chứng minh ở câu a) EF (EFG), CD (ABCD) 0.25
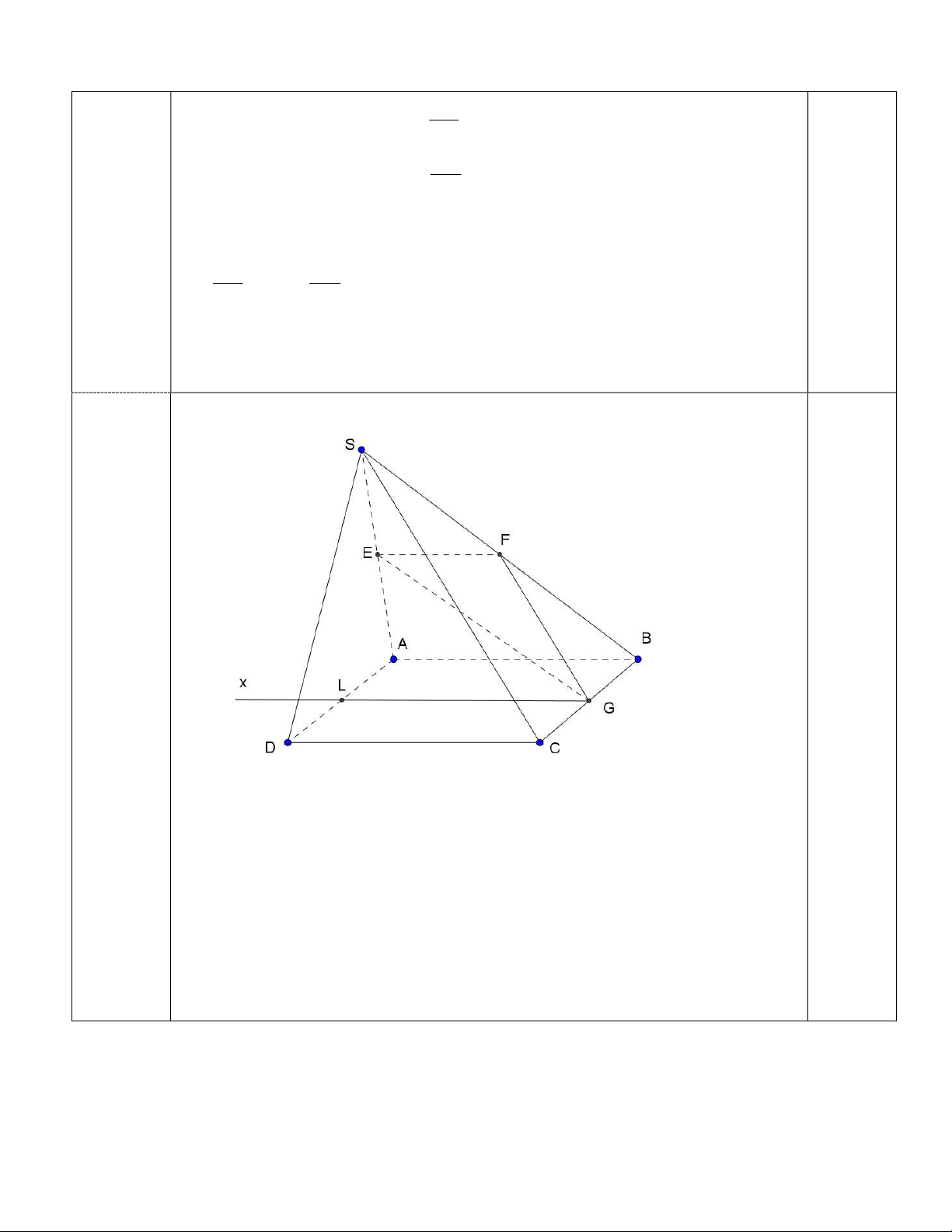
EFG ABCD Gx / / EF / / CD
Gx cắt AD tại L (trong (ABCD)) 0.25 Vậy L AD (EFG)
………………………………Hết………………………………….




