


Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ KIỂM TRA HỌC KỲ 1 THÀNH PHỐ HỒ CHÍ MINH (Năm học 2019 – 2020) TRƯỜNG THPT THĂNG LONG MÔN: TOÁN – KHỐI 11 (Đề chính thức)
Thời gian: 90 phút (không kể thời gian giao đề)
Họ tên học sinh: .................................................................................. Lớp: ............................ SBD: ............................
(Lưu ý: Học sinh làm bài trên giấy thi, không làm trên đề, không sử dụng tài liệu)
Câu 1 (2,0 điểm). Giải các phương trình sau a. 2sin 2x 1 0 . b. 3 3
sin x cos x sin x cos x . 4 Câu 2 (2,0 điểm).
a. Khai triển nhị thức P x 5 2 3 . 16 3 b. Cho nhị thức 2 Q x
. Tìm số hạng chứa 14
x trong khai triển của Q . x Câu 3 (2,0 điểm).
a. Một hộp kín chứa 8 viên bi trắng, 7 viên bi đỏ và 9 viên bi xanh. Lấy ngẫu nhiên 7 viên bi từ hộp kín.
Tính xác suất để trong các viên bi lấy ra có đúng 2 viên bi đỏ và 3 viên bi xanh.
b. Một hộp bóng đèn gồm có 50 chiếc trong đó bao gồm 30 chiếc loại I, 14 chiếc loại II và 6 chiếc loại III.
Lấy ngẫu nhiên từ hộp 8 chiếc bóng đèn. Tính xác suất để trong các bóng đèn lấy ra có ít nhất 5 chiếc loại III.
Câu 4 (1,0 điểm). Cho cấp số cộng u thỏa mãn u u u 5 và u 2u 10 . Tìm số hạng u và tổng 12 số n 2 3 5 7 6 12 hạng đầu tiên S . 12
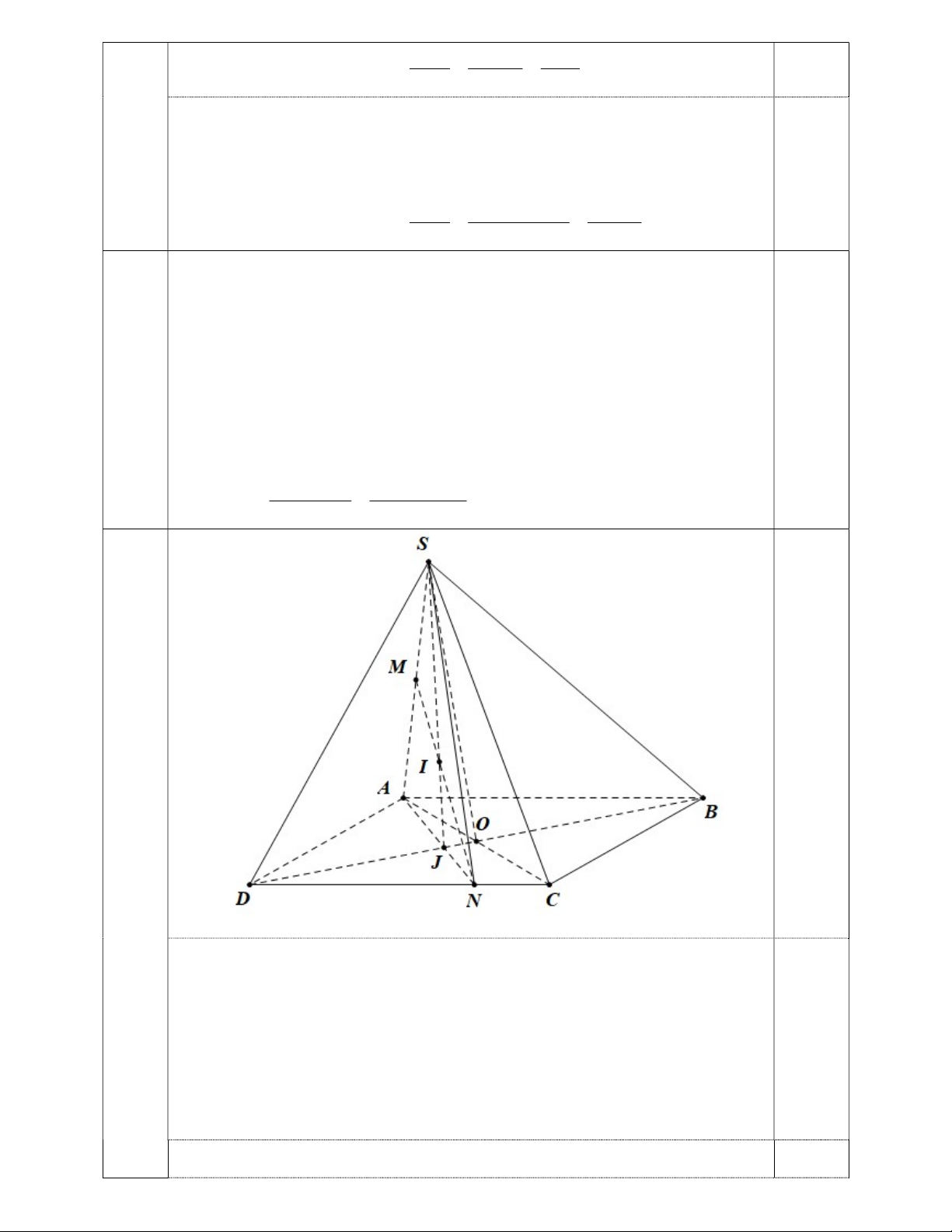
Câu 5 (3,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, hai đường chéo AC và BD cắt nhau tại O.
Điểm M là trung điểm SA, điểm N thuộc cạnh CD sao cho ND = 3NC.
a. Tìm giao tuyến của hai mặt phẳng (SAC) VÀ (SBD).
b. Chứng minh rằng đường thẳng SC song song với mặt phẳng (OMN).
c. Tìm giao điểm của đường thẳng MN với mặt phẳng (SBD). ------Hết------ TRƯỜNG THPT THĂNG LONG
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ I (NH 2019 – 2020) Môn: Toán – Khối 11 THANG CÂU ĐÁP ÁN ĐIỂM a. 2sin 2x 1 0 sin 2x sin 4 4 6 0.25 2x k2 4 6 0.25 2x k2 4 6 5 x k 24 0.5 13 x k 1 24 b. 3 3
sin x cos x sin x cos x sin x cos x1 sin x cos x 0 0.25 sin x cos x 0 1 0.25 sin x cos x 0 cos x 0 4 0.25 sin 2x 2 VN 3 x k 0.25 4 a.
P 2x 35 C 2x5 C 2x4 3 C 2x3 32 0 1 2 5 5 5 0.5
C 2x2 33 C 2x34 C 35 3 4 5 5 5 5 5 4 3 2
32x 240x 720x 1080x 810x 243. 0.5 16 3 b. 2 Q x x Số hạng thứ k 1 là 2 T C x k k 16 k k 3 2 1 16 x 0.25 3 k k 322k C x 16 k x C 3 k k 323k x 16 0.25 Số hạng T k k . k 1 chứa 14 x khi chỉ khi 32 3 14 6 0.25
Vậy số hạng cần tìm là T C 36 6 323.6 14 x 5837832x . 0.25 7 16 a.
Số phần tử của không gian mẫu là n 7 C 346104 . 0.25 24 3
Gọi A:“ các viên bi lấy ra có đúng 2 viên bi đỏ và 3 viên bi xanh”. 0.25 Suy ra n A 2 3 1 C C C 14112 . 0.25 7 9 8 0.25 n A 14112 196
Xác suất của biến cố A là P A . n 346104 4807 b.
Số phần tử của không gian mẫu n 8 C . 0.25 50
Gọi B :“ các bóng đèn lấy ra có ít nhất 5 chiếc loại III ”. 0.25 Suy ra n B 5 3 6 2 C C C C . 6 44 6 44 0.25 5 3 6 2 n B C C C C 17
Xác suất của biến cố B là P B 6 44 6 44 . 0.25 n 8 C 113505 50 Ta có u u u 5
u d u 2d u 4d 5 0.25 2 3 5 1 1 1 u 2u 10
u 6d 2 u 5d 10 7 6 1 1 u d 5 1 u 4d 10 1 4 u 2 1 0.25 d 3
Suy ra u u 11d 2 11 3 3 1, 12 1 0.25 12u u 12 2 31 1 12 S 1 74 . 12 0.25 2 2 5 0.25
Học sinh chỉ cần vẽ đúng nét đứt, nét liền hình chóp S.ABCD .
a. Tìm giao tuyến của hai mặt phẳng SAC và SBD .
Ta có S là điểm chung của SAC và SBD (1) 0.25 Mà O AC BD O AC SAC OSAC Suy ra . O BD SBD OSBD
Suy ra O là điểm chung của SCA và SBD (2) 0.25
Từ (1) và (2) suy ra giao tuyến của SAC và SBD là SO . 0.25
b. Chứng minh rằng đường thẳng SC song song với mặt phẳng OMN .
Ta có O là trung điểm AC và M là trung điểm SA nên OM là đường trung bình của
tam giác SAC , suy ra OM SC . 0.25 SC OM
Xét đường thẳng SC và mặt phẳng OMN , ta có O
M OMN SC OMN . 3 x 0.25 SC OMN
c. Tìm giao điểm của đường thẳng MN với mặt phẳng SBD . Ta có MN SAN . 0.25
Xét hai mặt phẳng SAN và SBD , ta có
S là điểm chung của SAN và SBD (3) J AN SAN J SAN
Gọi J AN BD , ta có J BD SBD J SBD
Suy ra J là điểm chung của SAN và SBD (4)
Từ (3) và (4) suy ra giao tuyến của SAN và SBD là SJ . 0.5
Gọi I SJ MN , suy ra I là giao điểm của MN và SBD . 0.25




