

Preview text:
Đề 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HỒ CHÍ MINH
ĐỀ KIỂM TRA HỌC KỲ I
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
Năm học: 2020 – 2021
Môn: TOÁN – Khối 11
Thời gian làm bài: 90 phút
(Không kể thời gian phát đề)
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Bài 1: (2,0 điểm) Giải các phương trình a) 2
2 sin x sin x 1 0 b)
2 cos x sin 3x sin 2x 0
Bài 2: (1,0 điểm) Cho tập hợp A 1; 2;3; 4;5;
6 . Gọi B là tập hợp tất cả các số tự nhiên gồm 4 chữ số đôi một
khác nhau được lấy từ A .
a) Tính số phần tử của B .
b) Chọn ngẫu nhiên 2 số thuộc B . Tính xác suất để trong hai số được chọn có đúng 1 số có mặt chữ số 3. n
Bài 3: (1,0 điểm) Tìm hệ số của 20
x trong khai triển Newton của 5
2x 4 biết n là số tự nhiên thỏa 2 2 2 A 50 A n 2n .
Bài 4: (1,0 điểm) Dùng phương pháp qui nạp toán học, chứng minh rằng với mọi số nguyên dương n ta luôn
có 13n 1 chia hết cho 12 . u 2u 0 1 5
Bài 5: (1,0 điểm) Tìm số hạng đầu tiên u và công sai d của cấp số cộng u biết . n 1
u u u u 14 1 2 3 4
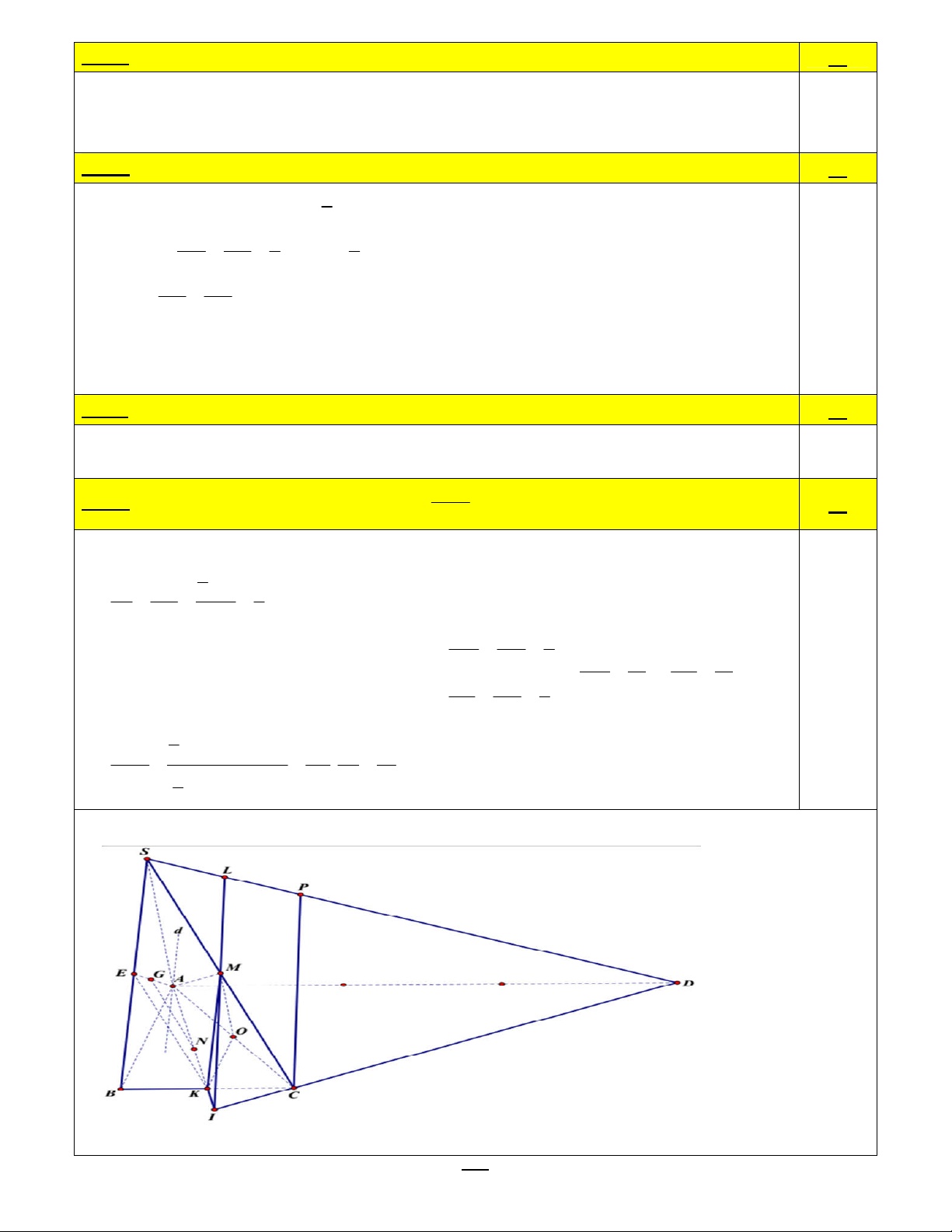
Bài 6: (4,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD / /BC và AD 3BC . Gọi M , K
lần lượt là trung điểm SC, BC .
a) Tìm giao tuyến của hai mặt phẳng SAB và AMK .
b) Gọi E, O lần lượt là trung điểm của SB, AC và G, N lần lượt là trọng tâm của các tam giác SAB ,
ABC. Chứng minh rằng: đường thẳng NG song song với mặt phẳng SBC.
c) Chứng minh rằng: mặt phẳng MOK song song với mặt phẳng SAB . S
d) Gọi I AK CD , L SD AMN . Tính tỉ số M IC . S L ID -----HẾT-----
ĐÁP ÁN & BIỂU ĐIỂM ĐỀ 2 Bài 1a: 2
2 sin x sin x 1 0 (1) 1đ x k 2 2 sin x 1 1 1 x
k 2 k Z 0.25x4 sin x 6 2 5 x k 2 6
Bài 1b: 2 cos x sin 3x sin 2x 0 (1) 1đ
1 2 cos x sin 3x 2sin x cos x 0 2 cos x sin 3x sin x 0 x k 2 cos x 0 0.25x4 x k k Z sin 3x sin x k x 4 2
Bài 2: A 1; 2;3; 4;5; 6 1đ a) 4
| B | A 360 0.25 6 b) 2 | | C 64620 . 0.25 360
Gọi C là biến cố: “ Trong 2 số được chọn có đúng một số có mặt chữ số 3” 0.25
Số các số không có chữ số 3 bằng 4
A 120 và số các số có mặt chữ số 3 là: 4 4
A A 240 . 5 6 5 1 1 C .C 160
Vậy xác suất cần tìm là P C 120 240 . 0.25 2 C 359 360 n
Bài 3: Tìm hệ số của 20
x trong khai triển 5 2x 4 biết 2 2 2 A 50 A n 2n . 1đ Điều kiện: n * n 2.
n 5 n 0.25x2 2 2
2A 50 A 2n n n n n n n 1 50 2 2 2 1 2 50 2 n 5 l k k k
Số hạng tổng quát của khai triển là: k
C .2x 4 5 5 = k .2k. 4 k C x 0.25 5 5 5 5 Hệ số của 20
x ứng với 5k 20 k 4. 0.25
Vậy hệ số cần tìm là: C .2 . 4 1 4 4 3 20. 5
Bài 4: Dùng qui nạp, CMR với mọi số nguyên dương n ta luôn có 13n 1 chia hết cho 12. 1đ n = 1: 1 13 1 12 12 (đúng). 0.25
Giả sử với n = k (kN*) ta có: 13k 1 12 0.25 Ta chứng minh: k 1 13 1 12 0.25 Ta có: k 1 k k 13
1 13.13 1 1313 1 12 12 0.25 Vậy ta có đpcm. u 2u 0 1 5
Bài 5: Tìm u và công sai d biết . 1đ 1
u u u u 14 1 2 3 4 u
2 u 4d 0 3
u 8d 0 d 3 1 1 1 Gt . 0.25x4
u u d u 2d u 3d 14 4u 6d 14 u 8 1 1 1 1 1 1
Bài 6a: Tìm giao tuyến của SAB và AMK . 1đ
ASAB AMK SB / /MK
SAB AMK d, d qua ,
A d / /SB / /MK. 0.25x4
SB SAB; MK AMK
Bài 6b: Chứng minh rằng NG / / SBC . 1đ 2
Gọi E là trung điểm SB GA AE 1 3 NK BK 1 2 BK / / AD AN AK 2 NA AD 2 3 AG AN 1 , 2 NG / / KE 0.25x4 AE AK
NG SBC NG / / KE
NG / / SBC
KE SBC
Bài 6c: Chứng minh rằng MOK / / SAB . 1đ MK / /SB
MOK / / SAB 0.25 x4 OK / / AB S
Bài 6d: I AK CD , L AMN SD . Tính M IC . 1đ S L ID
Trong (SCD): IM SD L L SD AMN . 1 BC IC KC 1 2 ID AD 3BC 6 LM SM 1 CP SC 2 LM 5 IM 7
Trong (SCD), dựng CP // LI (PSD). Khi đó: 0.25x4 PC DC 5 LI 12 IL 12 LI DI 6 1
MI.IC.sin MIC S MI IC 7 M IC 2 . S 1 LI ID L ID 72 LI.I . D sin LID 2 HẾT




