


Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO NGHỆ AN
ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2016-2017
TRƯỜNG THPT QUỲNH LƯU I MÔN TOÁN : LỚP 11
Thời gian làm bài: 90 phút ( không kể thời gian giao đề ) Câu 1. (2,0 điểm).
Giải các phương trình sau: a) 2cos 2 x – sinx + 1 = 0
b) (2cosx1)(cosx+2sinx)+sinx = sin2x 1 n
Câu 2.(1,0điểm) Viết dạng khai triển biểu thức x
. Tìm hệ số của x8 trong khai triển x2 1 14 của: x (x 0) x2 Câu 3. (2,0 điểm)
Để kiểm tra chất lượng sản phẩm từ một công ty sữa, người ta đã gửi đến bộ phận kiểm nghiệm
6 hộp sữa cam và 5 hộp sữa dâu. Bộ phận kiểm nghiệm chọn 4 hộp sữa để phân tích mẫu.
a) Tính xác suất để 4 hộp sữa được chọn cùng một loại.
b) Tính xác suất để 4 hộp sữa được chọn có ít nhất 1 hộp sữa dâu.
Câu 4. (1,0 điểm) Tìm số hạng đầu và công sai của cấp số cộng có số ha ̣ng thứ 8 bằng 15 và
tổng của của 9 số ha ̣ng đầu tiên là 81. Câu 5. (3,0 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, O là giao điểm của AC và BD. Gọi
M là trung điểm của cạnh SB; lấy N, P lần lượt trên cạnh BC, SD sao cho BN = 2CN và SP=2PD.
a) Xác định giao tuyến của hai mặt phẳng (SAD) và (SBC)
b) Biết tam giác ABC, SAD đều cân đỉnh A; AE,AF là các đường phân giác trong các tam
giác ACD và SAB, kẻ EH SD( H SC ). Chứng minh: OM (SCD); HF (SAD).
c) Tìm giao điểm của đường thẳng CP và mặt (AMN).
Câu 6. (1,0 điểm) Tìm GTNN của hàm số: ( o c sx-1)( o c s2x-2cosx+1) 4 2 y o c s x sin x
(x k ,k ) 3 x 3 3 3 2 2 sin x( o c s o c s )(1 tan ) 5 5 2 - Hết -
Họ và tên: ………………………………………………..Số báo danh………………….
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KỲ I - MÔN TOÁN 11( 2016 - 2017 ) Câu 1: (2,0 đ)
a) 2( 1- sin 2 x) – sinx +1 = 0 2- 2 sin 2 x – sinx +1 = 0
2 sin 2 x + sinx - 3 = 0 (sinx 1)(2sinx 3) 0 0.5 sin x 1 3
sinx =1 x = + k2 (k )
sin x (Loai) 2 0.5 2
b) (2cosx1)(cosx+2sinx) = 2sinxcosx-sinx
(2cosx1)(cosx+sinx) = 0 0,5 x k2 2cosx1 0 3 (k ) cosx+sinx 0 0.5 x k 4 1 n n k n k 1 k Câu 2: (1,0 đ) x C x ( ) hoặc x2 n 2 k0 x 1 n 0 n 1 n1 1 2 n2 1 2 k n x 1 1
C x C x ( )C x ( ) ... k C x ( k ) n C ... ( n ) x2 n n n n n x2 x2 x2 x2 1 14 0,5 SHTQ k
k 14k 2k k k 14 k 3 của KTr: x C (1) x x C (1) x 2 là: 14 14 x
Ta phải tìm k sao cho : 14 k 3 8 k 2 0,5
Vậy hệ số của x8 trong khai triển là C2 14 91
Câu 3. (2, 0 điểm)
a) Tính xác suất để 4 hộp sữa được chọn cùng một loại.
Không gian mẫu : Chọn 4 trong 11 hộp sữa để kiểm tra n( ) = 4 C =330 0.25 11
Gọi A là biến cố “4 hộp sữa được chọn cùng một loại”. +) TH1: 4 hộp sữa cam. 4 C = 15(cách chọn) 6 +)TH 2 :4 hộp sữa dâu. 4 C = 5(cách chọn) 0.5 5 Suy ra n(A) =20 n A 20 2 0.25 P(A) = n 330 33
b) Gọi B là biến cố “4 hộp sữa được chọn có ít nhất 1 hộp sữa dâu ”
Gọi B là biến cố “chọn được 4 hộp sữa cam” 4 0,5 n (B) C 6 15 n (B) 15 1 P (B) n () 330 22 1 21
P(B) 1 P(B) 1 0,5 22 22 Câu 4. (1,0 điểm) u 7d 15 u 15 1 0,5 Ta co 8 ́: 9(2u 8d) S 81 1 9 81 2 u 7d 15 d 2 1 0,5 u 4d 9 u 1 1 1
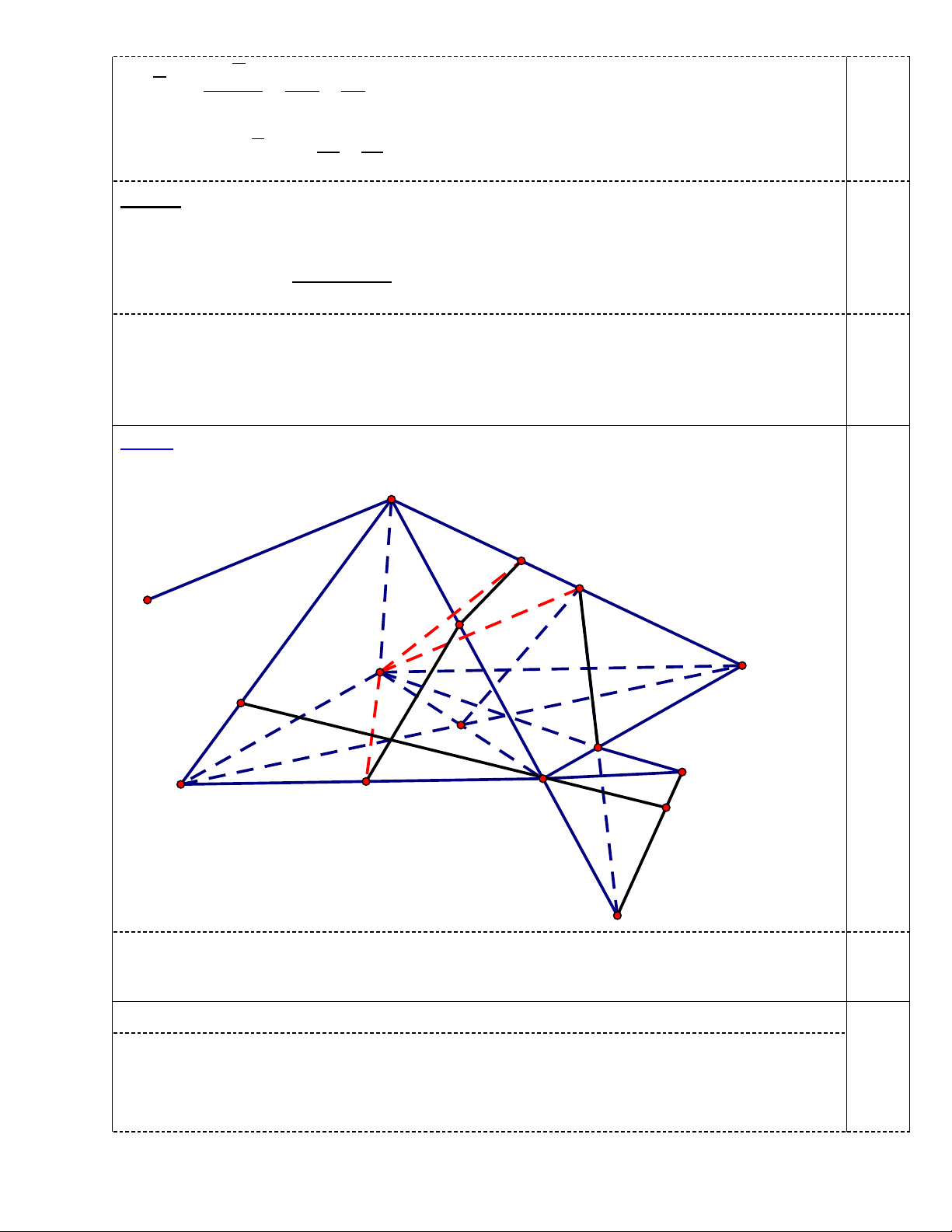
Bài 5. (3, 0 điểm) Vẽ hình: S 0.5đ F M x H A B P N O I D C E Q K
a) Hai mp (SAD) và (SBC) có điểm S chung, lần lựợt chứa 2 đường song song
AD BC SAD SBC Sx và Sx AD BC 0.5
b) (1,0 Điểm)
Trong tam giác SBD ta có OM là đường trung bình. Do đó: OM // SD OM // SD,SD (SCD) OM // (SCD) OM (SCD) 0,25 Từ HS DE AD AS SF (gt) HF BC 0,5 HC EC AC AB FB
mà BC// AD HF AD ; AD (SAD), HF (SAD) HF / /(SAD) 0.25
c) Trong (ABCD) ta có: AN DC I 0,25
ICD (SCD) I(SCD);IAN I(AMN) I là điểm chung thứ 1 Trong (SBC): SM 1 CN 1
MN không song song SC MN SC K SB 2 CB 3 0,5
K SC (SCD) K (SCD); K MN K (AMN) K là điểm chung thứ 2
(SCD) (AMN) = IK. Gọi PC IK = Q thì Q là giao điểm của CP và (AMN). 0,25
Bài 6. (1, 0 điểm) 1 osx c 1 osx c 3 x x 3 ( ) 2(tan tan ) ( osx- c 1)( os2x c -2cosx+1) s inx s inx 2 2 3 x 1 x x 3 3 3 2 2 2 2 2 2 sin x( os c os c )(1 tan ) (1 tan ) (1 tan ) 5 5 2 2 2 2 x 1 o c sx 3 sinx.cosx ( Vì tan và 3 3 o c s o c s 1 ) 2 sinx 5 5 2 2 0,5 1 o c s2x 1 o c s2x 1 sin 2x sin 2x 2 y ( ) sin2x = - 1 2 2 2 4 2 2 Đặt t = sin2x, t t 1
t 1, (ycbt) : Tìm GTNN : g(t) 1, trên [-1 ; 1] 4 2 Đỉnh I( 1
-1; );Lập BBT hàm số y=g(t) trên [-1 ; 1] 4 0,5
Suy ra GTNN của hàm số f(x) bằng 1 đạt khi sin2x= -1 hay x
k,k 4 4
Lưu ý: Mọi cách làm khác có đầy đủ ý, lập luận chắc chắn đều được điểm tối đa.




