Đề thi HK1 Toán 11 năm học 2018 – 2019 trường THPT Thị Xã Quảng Trị

SỞ GD&ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2018 - 2019
TRƯỜNG THPT TX QUẢNG TRỊ MÔN TOÁN KHỐI 11 NC (Đề số 1) ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1 (2,0đ). Giải các phương trình sau: 1) tan x  3  0.
2) 3 sin x  cos x  2.
Câu 2 (2,0đ). Cho A là tập hợp các số từ nhiên từ 1 đến 25. Lấy ngẫu nhiên 5 số từ tập
A . Tính xác suất để:
1) Trong 5 số được lấy có đúng 2 số chẵn.
2) Trong 5 số được lấy có ít nhất 2 số chia hết cho 3.
Câu 3 (1,0đ). Trong mặt phẳng Oxy , cho đường tròn 2 2
(C) : (x 1)  ( y  2)  9. Viết
phương trình đường tròn (C ') là ảnh của đường tròn (C) qua phép đồng dạng có được
bằng cách thực hiện liên tiếp phép đối xứng trục Ox và phép vị tự ( V O;2) .
Câu 4 (3,0đ). Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác SBC .
1) Tìm giao tuyến của mp(SAC) và mp(SBD) , mp SGD và mp BCD.
2) Tìm giao điểm K của đường thẳng AG và mp SBD.
3) Trên tia đối của tia BA lấy điểm E sao cho BE  2BA , M thuộc cạnh SE sao IS
cho ME  2MS , I là giao điểm của (MBD) và SC . Tính . IC
Câu 5 (1,0đ). Tìm số hạng chứa 5
x trong khai triển của biểu thức  x  9 2 3 .   
Câu 6 (1,0đ). Tìm m để phương trình sau có nghiệm x    ;  . 4   
2(sin x  cos x) - sin 2x  m
-------------------Hết--------------------
SỞ GD&ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2018 - 2019
TRƯỜNG THPT TX QUẢNG TRỊ MÔN TOÁN KHỐI 11 NC (Đề số 2) ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1 (2,0đ). Giải các phương trình sau: 1) tan x  3  0.
2) sin x  3 cos x  2.
Câu 2 (2,0đ). Cho A là tập hợp các số từ nhiên từ 1 đến 23. Lấy ngẫu nhiên 4 số từ tập
A . Tính xác suất để:
1) Trong 4 số được lấy có đúng 2 số chẵn.
2) Trong 4 số được lấy có ít nhất 2 số chia hết cho 3.
Câu 3 (1,0đ). Trong mặt phẳng Oxy , cho đường tròn 2 2
(C) : (x  2)  ( y 1)  4 . Viết
phương trình đường tròn (C ') là ảnh của đường tròn (C) qua phép đồng dạng có được
bằng cách thực hiện liên tiếp phép đối xứng trục Oy và phép vị tự ( V O;3) .
Câu 4 (3,0đ). Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi G là trọng tâm tam giác SAB .
1) Tìm giao tuyến của mp(SAC) và mp(SBD) , mp SGC  và mp ABC .
2) Tìm giao điểm K của đường thẳng DG và mp  SAC .
3) Trên tia đối của tia AD lấy điểm E sao cho AE  2 AD , M thuộc cạnh SE IS
sao cho ME  2MS , I là giao điểm của (MAC) và SB . Tính . IB
Câu 5 (1,0đ). Tìm số hạng chứa 5
x trong khai triển của biểu thức  x  9 3 2 .  9 
Câu 6 (1,0đ). Tìm m để phương trình sau có nghiệm x   ;  . 4   
2(sin x  cos x) - sin 2x  m
-------------------Hết--------------------
SỞ GD&ĐT QUẢNG TRỊ
ĐÁP ÁN THI HỌC KỲ I NĂM HỌC 2018 - 2019
TRƯỜNG THPT TX QUẢNG TRỊ MÔN TOÁN KHỐI 11 ĐỀ SỐ 1 Câu Lời giải Điểm C1.1.  1.00đ
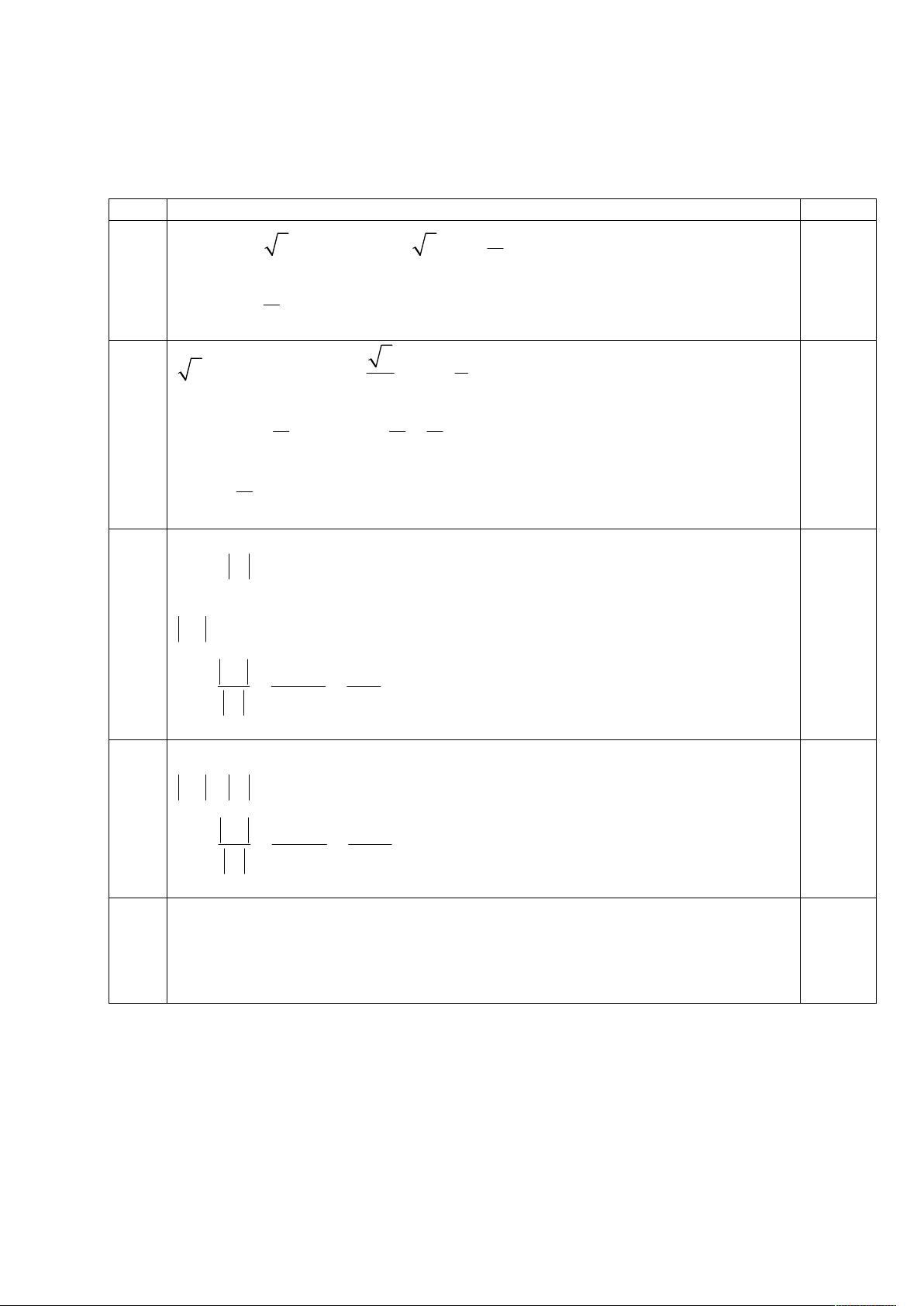
tan x  3  0  tan x  3  tan 0.50đ 3   x   k 3 0.50đ C1.2. 3 1 1.00đ
3 sin x  cos x  2  sin x  cos x  1 0.25đ 2 2       sin x   1  x    k 2   . 0.50đ  6  6 2   x   k 2 3 0.25đ C2.1. 1.00đ Ta có: 5   C  53130 0.25đ 25
Gọi B là biến cố: “Trong 5 số được lấy có đúng 2 số chẵn” 2 3
  C .C  18876 0.50đ B 12 13  B 18876 286 P    0.25đ B  53130 805
C2.2. Gọi C là biến cố: “Trong 5 số được lấy có ít nhất 2 số chia hết cho 3” 1.00đ 0.50đ 1 4 5
    (C .C  C )  27902 C 8 17 17 C 27902 1993 P    0.50đ C  53130 3795
C3.1. + Ta có: (C) có tâm I(1; 2) và R = 3 1.00đ I(1;2)  § V Ox I (1;2)  ( O ;2  )  I '(2;4) 0.25đ 1 0.25đ
Vậy (C’) có tâm I’(2; -4) và R’ = 2R = 6 0.25đ
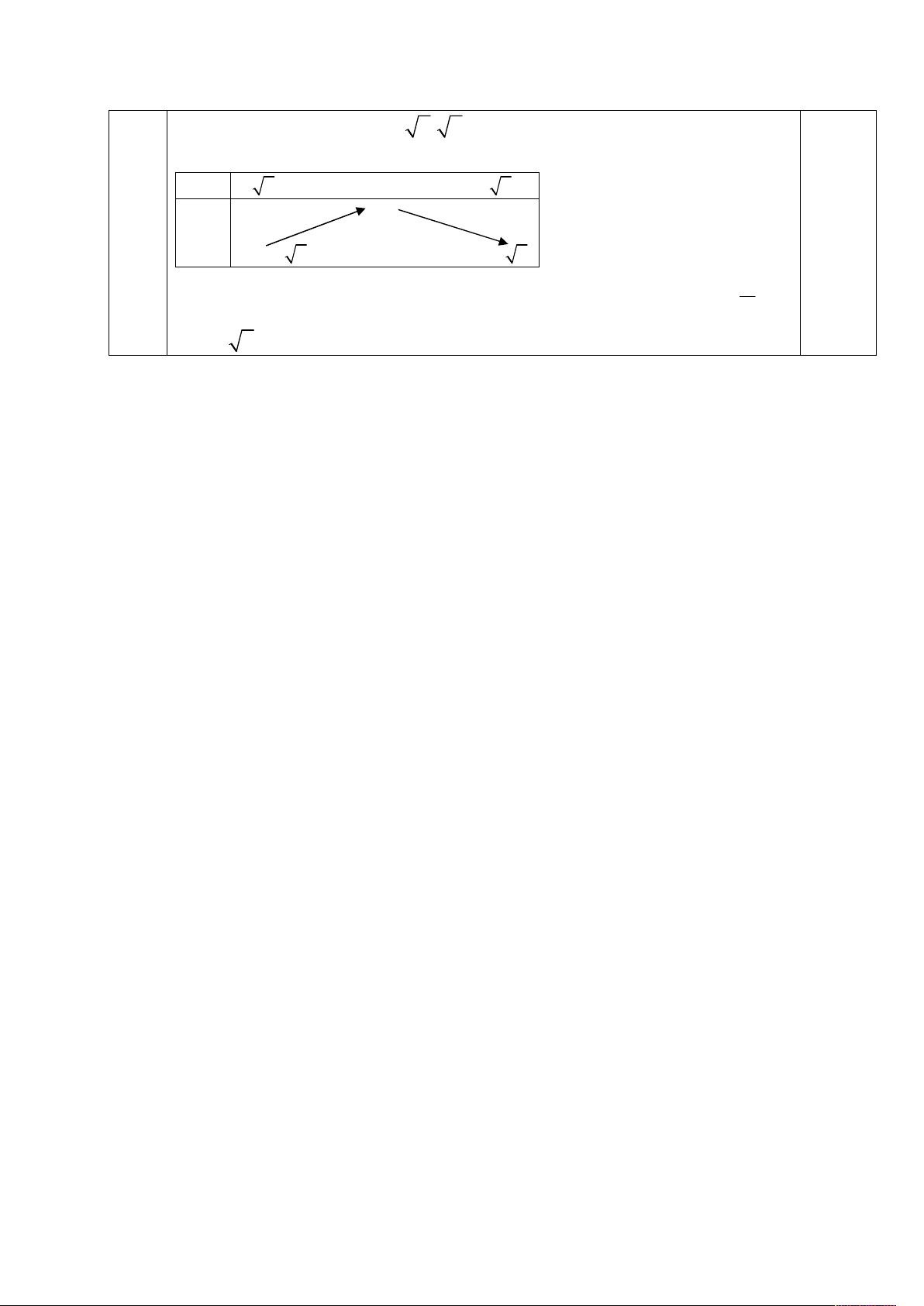
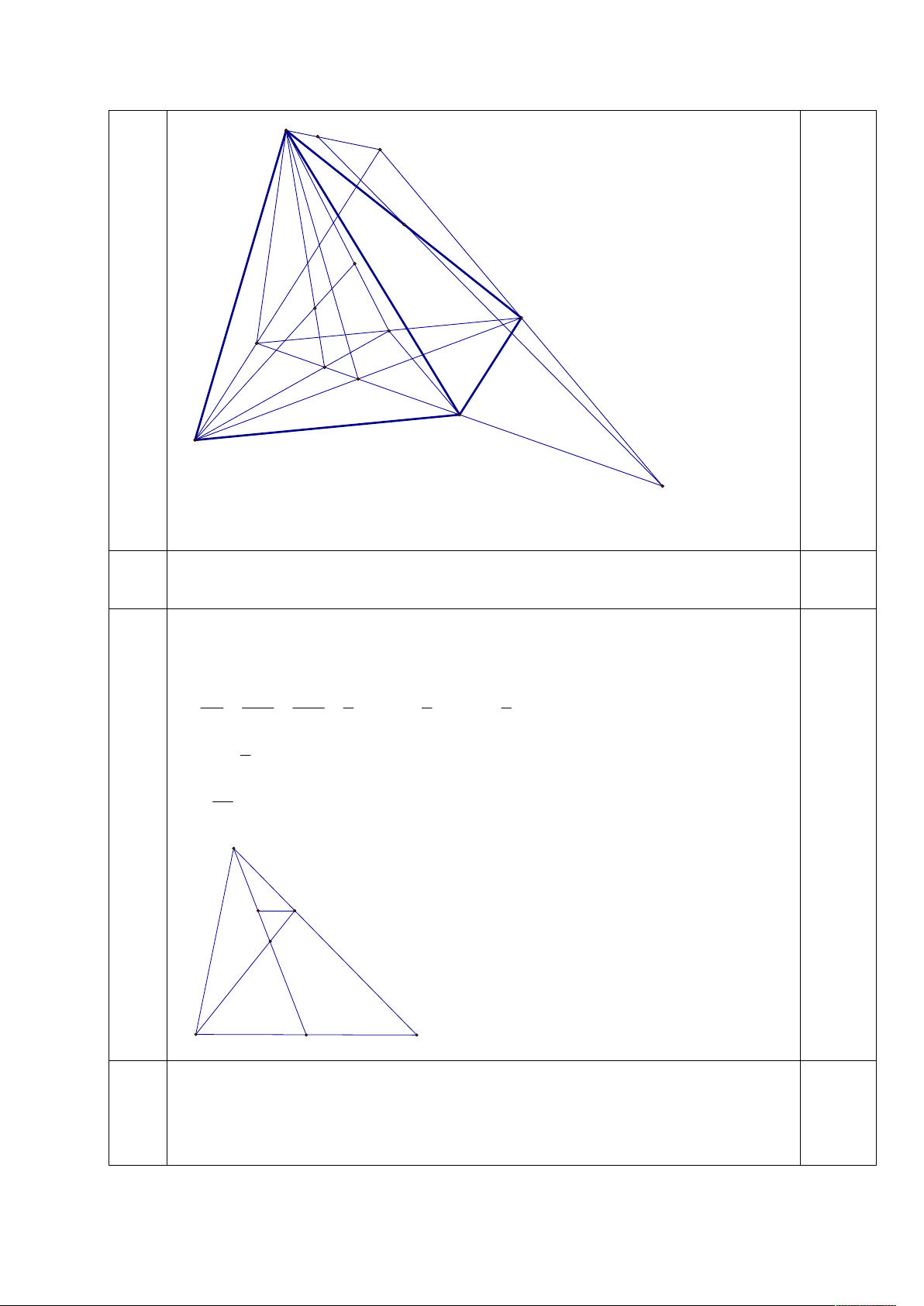
Nên (C’): (x – 2)2 + (y +4)2 = 36 0.25đ C4.1. S M 1.00đ E I G K C P B Q O D A F 0.5đ
+ Gọi O  AC  BD  (SAC)  (SBD)  SO
+ Gọi P là trung điểm của BC  (S D
G )  (BCD)  PD 0.5đ
C4.2. Gọi Q  AP  BD, K  AG  SQ  ( D SB ) 0.5đ 1.00đ
 K  AG  (SBD) 0.5đ
C4.3. + Gọi F  CE  D
B ;I  SC  MF  (MBD)
1.00đ  I  (M D B )  SC 0.25đ
+ Ta có C là trung điểm của EF, trong tam giác SEF kẻ MN//EF. IN MN MN 1 1 1      IN  IC, SN  SC 0.25đ IC FC EC 3 3 3 1 0.25đ  IS 
(IC  SC)  3IS=IC  SC  4IS=2SC  2IS=SC 3 IS 0.25đ Hay  1 IC S M N I F E C C5. 9 9 9 k k 9k k k 9k k
1.00đ Ta có:  2x  3  C (2x) .(3)  C 2 .( 3  ) .x  9  . 9 0.50đ k 0 k 0 5
Vậy số hạng chứa x trong khai triển trên là 5 4 5 5 5 2 .( 3
 ) .C .x  326592x 0.50đ 9 C6.   
1.00đ Đặt t  s inx  osx c , do x    ; 
 t   2; 2  4      0.25đ Pttt: 2
t  2t  1  m 0.25đ Xét 2
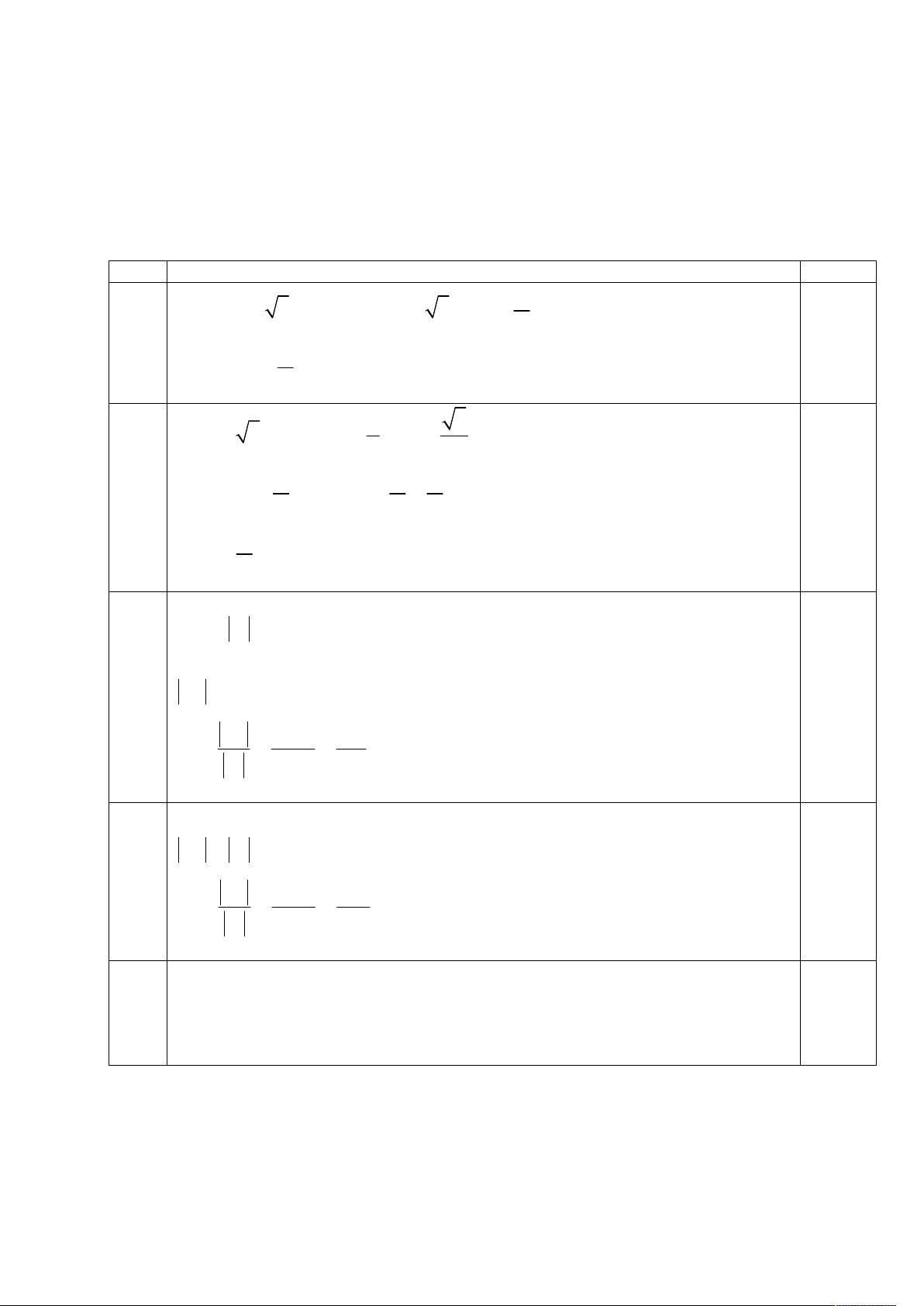
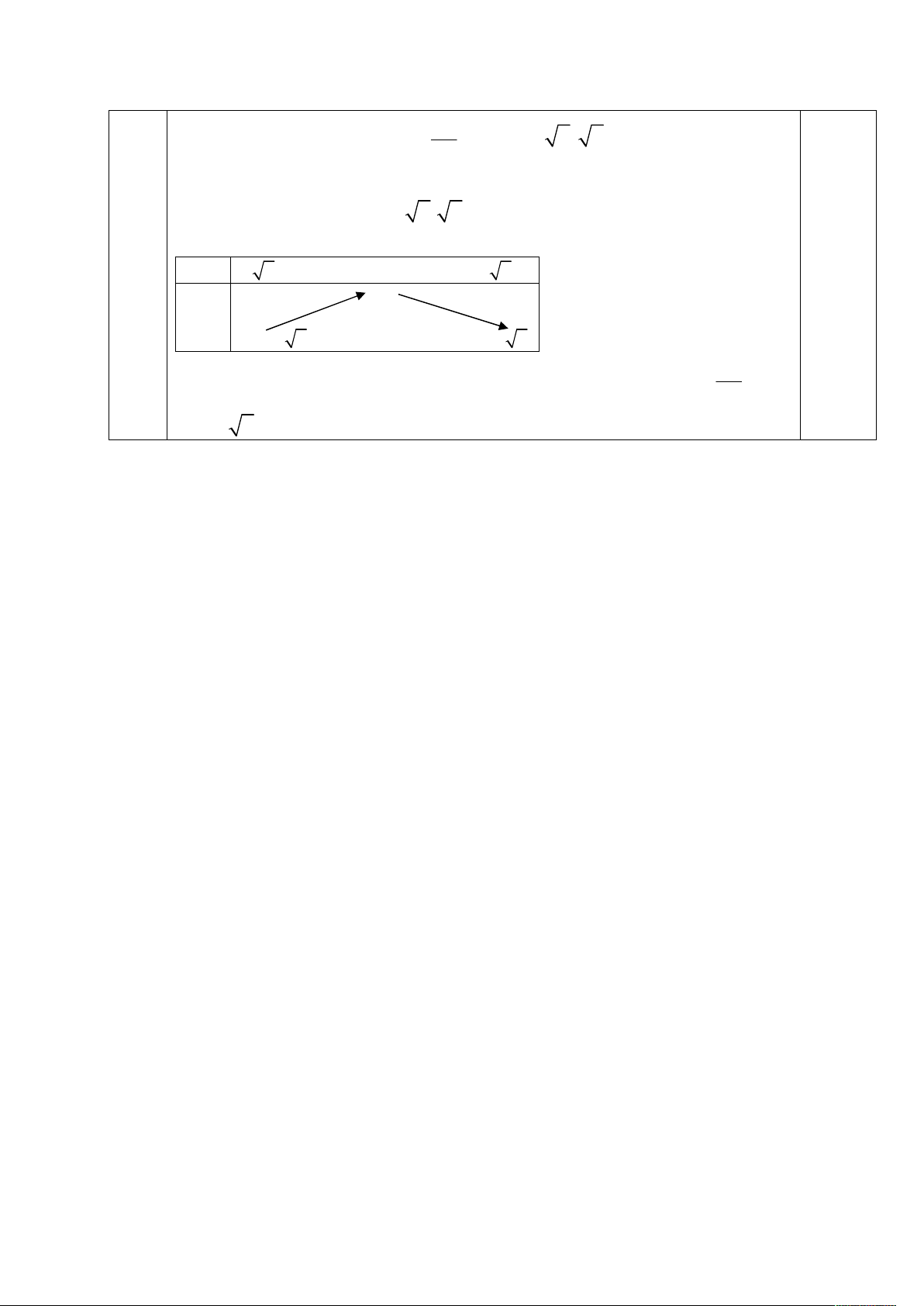
f (t)  t  2t  1,t  - 2; 2    BBT t  2 1 2 f(t) 0 2 0.25đ 1   2 2 1   2 2 0.25đ   
Dựa vào bbt ta có phương trình đã cho có nghiệm x    ;  khi 4   
1  2 2  m  2
Ngoài cách giải mà đáp án nêu ra nếu học sinh có cách giải khác thì tùy theo thang điểm mà cho điểm.
SỞ GD&ĐT QUẢNG TRỊ
ĐÁP ÁN THI HỌC KỲ I NĂM HỌC 2018 - 2019
TRƯỜNG THPT TX QUẢNG TRỊ MÔN TOÁN KHỐI 11 ĐỀ SỐ 2 Câu Lời giải Điểm C1.1.  1.00đ
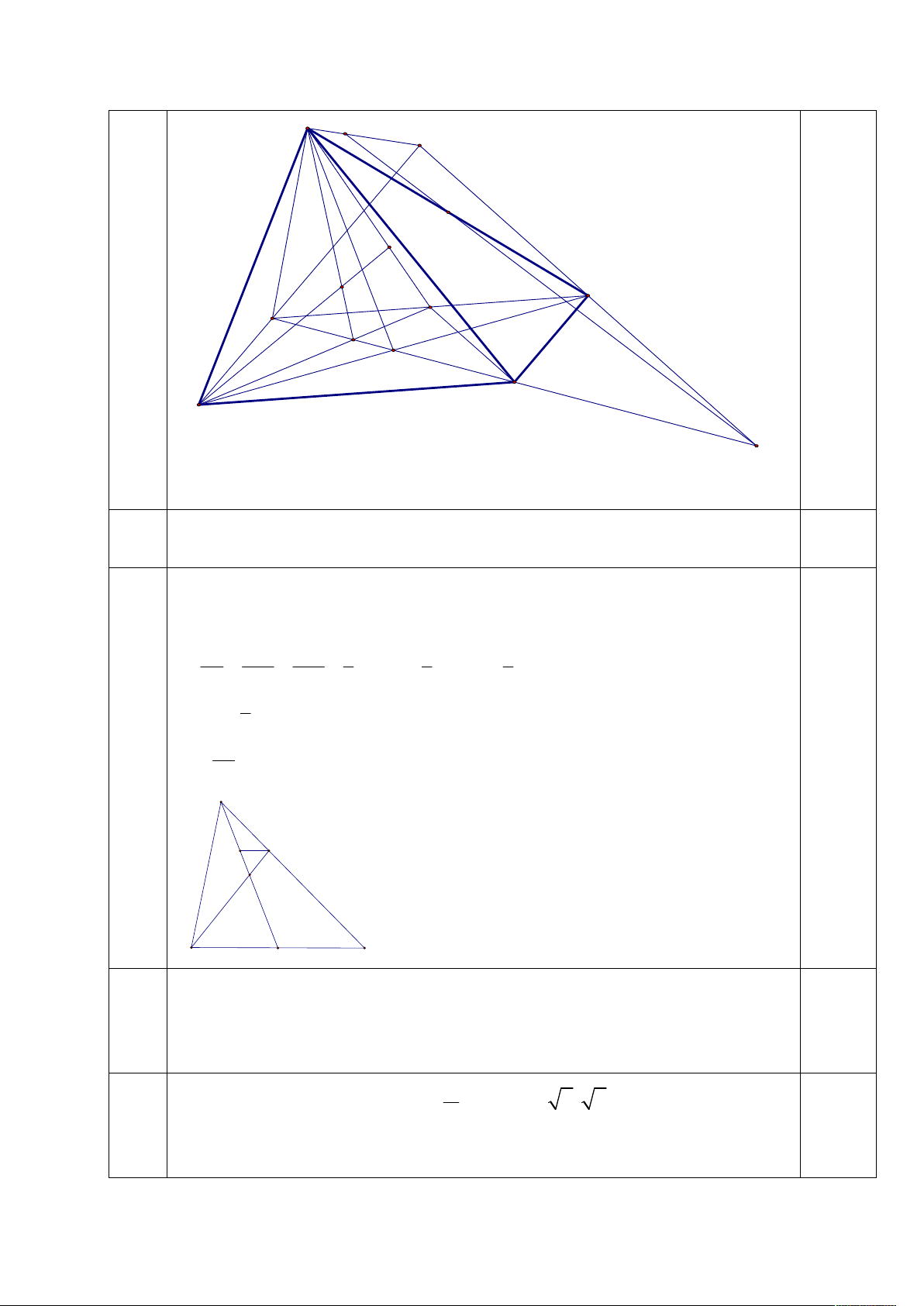
tan x  3  0  tan x   3   tan 0.50đ 3   x    k 3 0.50đ C1.2. 1 3 1.00đ sin x  3 cos x  2  sin x  cos x  1 0.25đ 2 2       sin x   1  x    k 2   . 0.50đ  3  3 2   x   k 2 6 0.25đ C2.1. 1.00đ Ta có: 4   C  8855 0.25đ 23
Gọi B là biến cố: “Trong 4 số được lấy có đúng 2 số chẵn” 2 2
  C .C  3630 0.50đ B 11 12  B 3630 66 P    0.25đ B  8855 161
C2.2. Gọi C là biến cố: “Trong 4 số được lấy có ít nhất 2 số chia hết cho 3” 1.00đ 0.50đ 1 3 4
    (C .C  C )  3115 C 7 16 16 C 3115 99 P    0.50đ C  8855 253
C3.1. + Ta có: (C) có tâm I(2; 1) và R = 2 1.00đ I(2;1)  §Oy I (2;1)  V(O;3  ) I '(6;3) 0.25đ 1 0.25đ
Vậy (C’) có tâm I’(-6; 3) và R’ = 3R = 6 0.25đ
Nên (C’): (x + 6)2 + (y - 3)2 = 36 0.25đ C4.1. S M 1.00đ E I G K B P A Q O C D 0.5đ F 0.5đ
+ Gọi O  AC  BD  (SAC)  (SBD)  SO
+ Gọi P là trung điểm của AB  (SGC)  ( ABC)  C P
C4.2. Gọi Q  DP  AC, K  DG  SQ  (SAC) 0.5đ 1.00đ
 K  DG  (SAC) 0.5đ
C4.3. + Gọi F  BE  AC;I  SB  MF  (MAC)
1.00đ  I  (MAC)  SB 0.25đ
+ Ta có B là trung điểm của EF, trong tam giác SEF kẻ MN//EF. IN MN MN 1 1 1      IN  IB, SN  SB 0.25đ IB FB EB 3 3 3 1 0.25đ  IS 
(IB  SB)  3IS=IB  SB  4IS=2SB  2IS=SB 3 IS 0.25đ Hay  1 IB S M N I F E B C5. 9 9 9 k k 9k k k 9k k
1.00đ Ta có: 3x  2  C (3x) .( 2)   C 3 .(2) .x  9  . 9 0.50đ k 0 k 0 5
Vậy số hạng chứa x trong khai triển trên là 5 4 5 5 5
3 .(2) .C .x  489888x 0.50đ 9 C6.  9 
1.00đ Đặt t  s inx  osx c , do x   ; 
 t   2; 2  4      0.25đ Pttt: 2
t  2t  1  m Xét 2
f (t)  t  2t  1,t  - 2; 2    0.25đ BBT t  2 1 2 f(t) 0 2 0.25đ 1   2 2 1   2 2  9  0.25đ
Dựa vào bbt ta có phương trình đã cho có nghiệm x   ;  khi 4   
1  2 2  m  2
Ngoài cách giải mà đáp án nêu ra nếu học sinh có cách giải khác thì tùy theo thang điểm mà cho điểm.