


Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HK I – NĂM HỌC 2019 – 2020 TP. HỒ CHÍ MINH MÔN TOÁN – LỚP 11 TRƯỜNG THCS-THPT
Thời gian làm bài: 90 phút (không kể thời gian phát đề) DIÊN HỒNG ĐỀ CHÍNH THỨC (Đề gồm 01 trang)
Bài 1. (2 điểm) Giải các phương trình sau: a) sin 2x 3 cos 2x 2 b) 2 2sin x 5cos x 4 0 Bài 2. (4 điểm)
a) Từ một hộp chứa 4 quả cầu màu đỏ, 5 quả cầu màu xanh và 7 quả cầu màu vàng. Lấy ngẫu
nhiên cùng lúc ra 4 quả cầu từ hộp đó. Tính xác suất sao cho 4 quả cầu được lấy ra có
đúng một quả cầu màu đỏ và không có quá hai quả cầu màu vàng.
b) Hai xạ thủ cùng bắn, mỗi người một viên đạn vào bia một cách độc lập với nhau. Xác suất
bắn trúng bia của hai xạ thủ lần lượt là 1 và 1 . Tính xác suất của biến cố có ít nhất một xạ 2 3
thủ không bắn trúng bia. c) Giải phương trình 2 2 3C nP 4A . n 1 2 n 20 2
d) Tìm hệ số của số hạng chứa 10 x trong khai triển 2 x . x u u 19
Bài 3. (1 điểm) Tính tổng 20 số hạng đầu của cấp số cộng u , n biết : 2 5 u u u 36 3 4 6
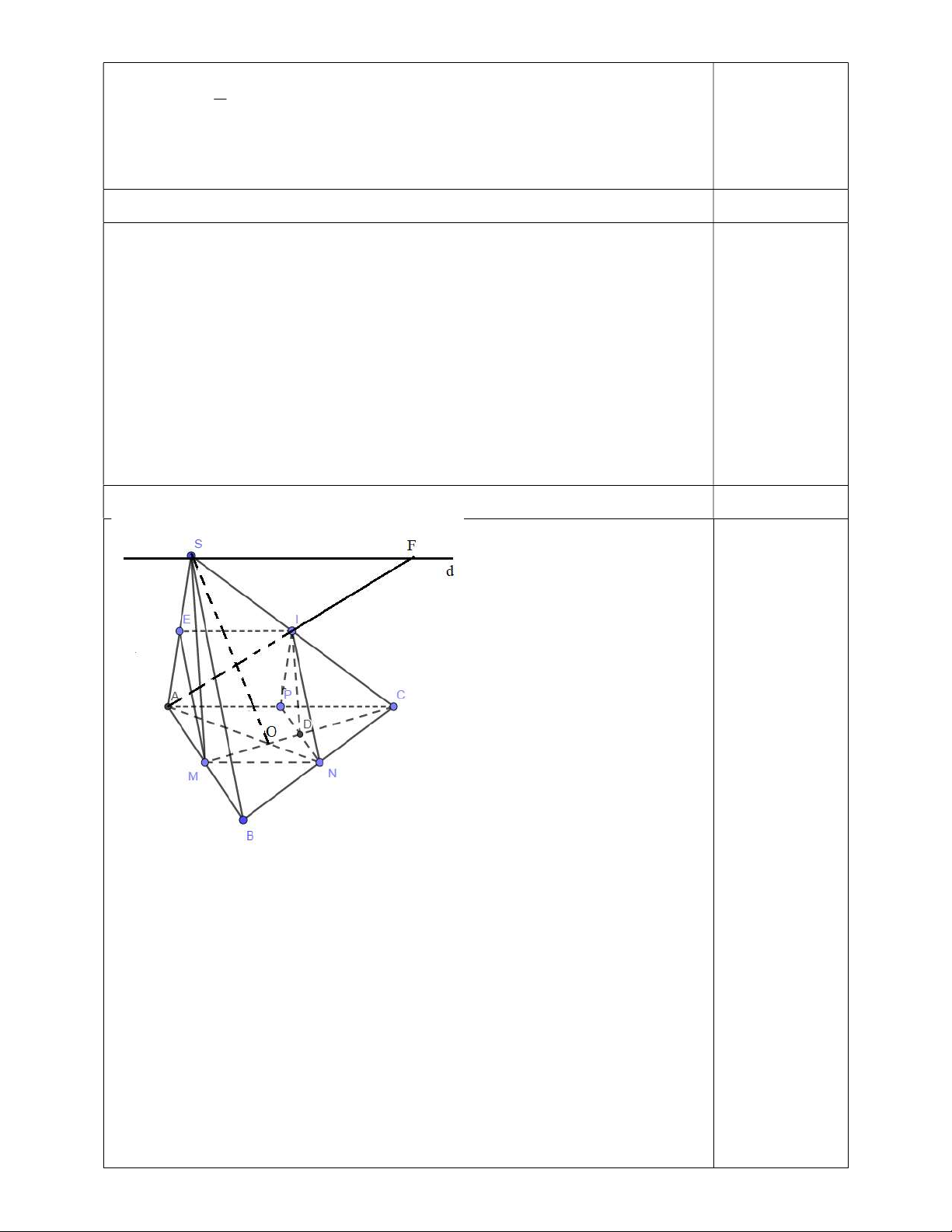
Bài 4. (3 điểm) Cho hình chóp S.ABC. Gọi M, N, P lần lượt là trung điểm của AB, BC, CA
a) Tìm giao tuyến của hai mặt phẳng (SAN) và (SCM); (SAC) và (SMN).
b) Gọi I là trung điểm của SC. Tìm giao điểm của AI với (SMN). c) Chứng minh: SM // (INP).
d) Xác định thiết diện của hình chóp cắt bởi (MNI).
----------- HẾT -----------
Học sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên học sinh: ...........................................................................................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ I – NĂM HỌC 2019 – 2020 TP. HỒ CHÍ MINH MÔN TOÁN – LỚP 11 TRƯỜNG THPT DIÊN HỒNG
Thời gian làm bài: 90 phút (không kể thời gian phát đề) HƯỚNG DẪN CHẤM ĐIỂM TỪNG NỘI DUNG TRẢ LỜI PHẦN Câu 1 (2 điểm) a) 3 sin 2x cos 2x 1 2 (0.5 điểm) sin 2 . x cos cos 2 . x sin 3 3 2 (0.25 điểm) sin 2x sin 3 4 x k (0.25 điểm) 24 5 x k (0.25 điểm) 24 a) 2 2sin x 5cos x 4 0 2 2
1 cos x 5cos x 4 0 (0.25 điểm) 2 2
cos x 5cos x 2 0 (0.25 điểm) cos x 2(l) (0.25 điểm) 1
cos x (n) x k2 (0.25 điểm) 2 6 Câu 2 (4 điểm) a) 1 3 1 2 1 1 1 2
C .C C .C .C C .C C . 740 (1 điểm) 4 5 4 5 7 4 5 7 b) P A 1 2 1 1 1 2 5 . . . 2 3 2 3 2 3 6 (1 điểm)
c) Điều kiện x 2, x (0.25 điểm) 2 2 3C nP 4A n 1 n 3.n 21! n ! (0.25 điểm) n n.2! 6 2! 1 ! n 2! 3 (0.25 điểm)
n n 12n 4nn 1 2 2 5n 15n 0 n 0(l) n 3 n 3(n) (0.25 điểm)
d) Số hạng tổng quát thứ k+1: k (0.25 điểm) 120 2 k k 2 k k 40 3 2 k C x C x 20 20 (0.25 điểm) x 40 3k 10 k 10 (0.25 điểm) 10 10 C 2 189190144 20 (0.25 điểm) Câu 3: (1 điểm) u u 19 2 5 u u u 36 3 4 6 u d u 4d 19 1 1
u 2d u 3d u 5d 36 (0.25 điểm) 1 1 1 (0.25 điểm) 2u 5d 19 1 3u 10d 36 1 (0.25 điểm) u 2 1 d 3 (0.25 điểm)
S 20.2 20.19.3: 2 610 20 Câu 4: (2 điểm) a) S (SAN ) (SCM ) (0.25 điểm) O AN (SAN)
Trong (ABC) gọi O AN CM O (0.25 điểm) CM (SCM ) (0.25 điểm) O (SAN) (SCM )
Vậy SO (SAN ) (SCM ) (0.25 điểm) S (SAC) (SMN ) AC (SAC) MN (SMN) MN / /AC (t / c dtb) (0.25 điểm)
(SAC) (SMN) d / / AC,S d (0.25 điểm) (0.25 điểm)
b) Trong (SAC) gọi F AI d F AI (0.25 điểm) F AI (SMN) F d (SMN)
c) Trong (ABC) gọi D CM PN (0.25 điểm)
Ta có PN là đường trung bình trong tam giác ABC, D thuộc PN nên D là (0.25 điểm) trung điểm CM Mà I là trung điểm SC.
Suy ra ID là đường trung bình trong tam giác SCM SM / /ID (1 điểm)
Mà ID (INP) nên SM / /(INP) d) Ta có I (SAC) (IMN) AC (SAC) MN (IMN) MN / /AC (t / c dtb)
(SAC) (SMN) d '/ / AC, I d ' (0.25 điểm) Gọi E d ' SA .
Vậy giao tuyến là tứ giác IEMN. (0.25 điểm) -HẾT-




