Đề thi học kì 1 Toán 11 năm 2019 – 2020 trường Giồng Ông Tố – TP HCM

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ I NĂM HỌC 2019-2020 TP HỒ CHÍ MINH Môn: TOÁN- KHỐI 11
TRƯỜNG THPT GIỒNG ÔNG TỐ
Thời gian làm bài: 90 phút, không kể thời gian phát đề ĐỀ CHÍNH THỨC (gồm có 01 trang)
Họ tên thí sinh:. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Lớp: . . . . . . . . . . . . . . . . . . . . . . . . Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 1. (1,5 điểm) Giải các phương trình lượng giác: sin x  2  cos 2 .
x 2) sin x  3 cos x  2 . Câu 2. (1.5 điểm)
Tìm số hạng không chứa x trong khai triển nhị thức 2 2 15 (x  ) ,  x  0 . x
Tìm số hạng chính giữa trong khai triển 10 (1 2x) . Câu 3. (1,5 điểm)
Một đề thi học kỳ có 5 câu hỏi được chọn từ bộ đề ôn tập gồm 30 câu. Có một học
sinh chỉ học thuộc được 23 câu trong bộ đề đó. Tính xác suất để học sinh này trả lời đúng cả 5 câu hỏi.
Xác suất sút bóng từ xa ghi bàn của đội A là 0,7. Trong trận chung kết đội A gặp đội
B, các cầu thủ của đội A đã thực hiện 5 lần sút xa. Tính xác suất để đội A ghi được 3
bàn thắng trong 5 tình huống sút xa đó. Câu 4. (1,5 điểm)
Cho cấp số cộng có 5 số hạng sao cho số hạng đầu là 2019 và số hạng cuối là 2020.
Tìm công sai và các số hạng của cấp số cộng này.
Cho cấp số nhân, biết u  3, q  2  1
. Hỏi số 768 là số hạng thứ mấy?
Câu 5. (4 điểm) Cho hình chóp SABCD có đáy ABCD là hình bình hành tâm O. Gọi M và
P lần lượt là trung điểm của cạnh SA và cạnh CD.
Tìm giao tuyến d của mặt phẳng (SAD) và mặt phẳng (MOP); giao tuyến của mặt phẳng (SAC) và (SBD).
Tìm giao điểm Q của đường thẳng AB và mặt phẳng (MOP).
Gọi K là giao điểm của đường thẳng DQ và đường thẳng AC, G là trọng tâm của tam
giác SAD. Chứng minh KG // (SBC).
Tìm thiết diện của mặt phẳng (MOP) với hình chóp SABCD. Thiết diện là hình gì? ---- Hết ----
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KÌ 1 NĂM HỌC 2019-2020
MÔN TOÁN 11- ĐỀ CHÍNH THỨC Câu Nội dung Điểm
1) Giải phương trình sin x  2 cos2 . x (0,75 điểm) 2 2
 sin x  2 1 2sin x  2sin x  sin x  3  0 0,25 sin x  1(n)   3  0,25 sin x   (l)  2 
Vậy phương trình có nghiệm x   k2 k  Z  0,25 Câu 2 1
2) Giải phương trình sin x  3 cos x  2 (0,75 điểm) 1 3   sin x  3 cos x  2   sin x  cos x  1
  cos .sin x  sin .cos x  1  0,25 2 2 3 3        5 s in x   1    x 
   k2  x    k2 0,25  3  3 2 6 5
Vậy phương trình có nghiệm x    k2 , k  Z 0,25 6 15  
1) Tìm số hạng không chứa x trong khai triển của nhị thức 2 2 x  , x  0    x  (0,75 điểm) Gọi số hạn
g tổng quát của khai triển là k k 2 15k  2  0,25 T  C (x )  , (k  15, k  N) k 1  15    x   k  k ( 2)k Câu 30 2 k k 303 T  C .x .  C .( 2  ) . k x 0,25 k 1  15 k 15 2 x
Yêu cầu bài toán  30  3k  0  k 10
Vậy số hạng không chứa x cần tìm là 10 10 0 T  C ( 2  ) .x  3075072 0,25 11 15
2) Tìm số hạng chính giữa trong khai triển 10 (1 2x) . ( 0,75 điểm)
Gọi số hạng tổng quát của khai triển là 10 T  C (1)  2 k k k x , (k  10, k  N) 0,25 k 1  10  
Khai triển có 11 số hạng nên số hạng chính giữa là số hạng thứ 6 0.25
Vậy số hạng chính giữa là 5 5 5 5 5 5
T  C .1.(2x)  C .2 .x  8064x 0,25 6 10 10
1) Một đề thi học kỳ có 5 câu hỏi được chọn từ bộ đề ôn tập gồm 30 câu. Có
một học sinh chỉ học thuộc được 23 câu trong bộ đề đó. Tính xác suất để học
sinh này trả lời đúng cả 5 câu hỏi. Câu ( 0,75 điểm) 3
Số phần tử không gian mẫu 5 n()  C 30 0,25
Gọi biến cố A: “Học sinh trả lời đúng cả 5 câu hỏi” 5 n( ) A  C 0,25 23 5 n( ) A C 4807 23 P( ) A     0, 24 5 n( 0,25 ) C 203 8 5 30
2) Xác suất sút bóng từ xa ghi bàn của đội A là 0,7. Trong trận chung kết đội
A gặp đội B, các cầu thủ của đội A đã thực hiện 5 lần sút xa. Tính xác suất
để đội A ghi được 3 bàn thắng trong 5 tình huống sút xa đó. (0,75 điểm )
Gọi biến cố E: “Trong 5 lần sút xa đội A ghi được 3 bàn thắng”
Ta có xác suất sút bóng từ xa ghi bàn của đội A là 0,7 nên xác suất sút bóng từ 0,25
xa không ghi bàn của đội A là 0,3 3 3087 3 2 P(E)  .(0, 7) .(0,3) C  0,5 5 10000
1) Cho cấp số cộng có 5 số hạng sao cho số hạng đầu là 2019 và số hạng cuối
là 2020. Tìm công sai và các số hạng của cấp số cộng này. ( 0,75 điểm) u  2019 u   2019 Ta có: 1  1   0,25 u  2020  u  4d  2020 5  1 u   2019 1   0,25 d   0, 25
Câu u  2019; u  2019,25; u  2019,5;u  2019,75;u  2020 4 1 2 3 4 5 0,25
2) Cho cấp số nhân, biết u  3, q  2 1
. Hỏi số 768 là số hạng thứ mấy? ( 0,75 điểm) Số hạng tổng quát 1 u u . n q   0,25 n 1 n 1  n 1 768 3.( 2) 256 ( 2)         n 1  8 0,25
Vậy số 768 là số hạng thứ 9 0,25
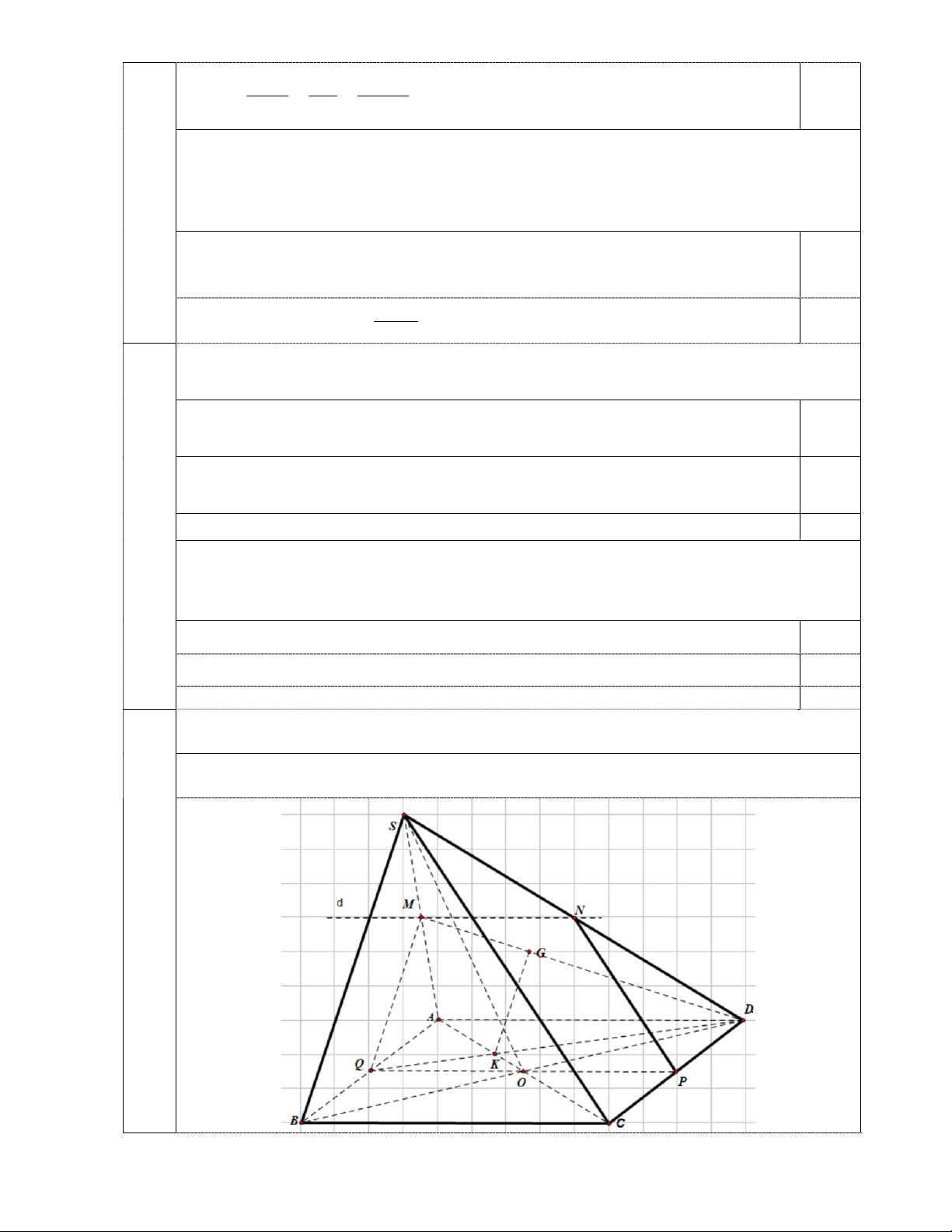
Cho hình chóp SABCD có đáy ABCD là hình bình hành tâm O. Gọi M và P lần
lượt là trung điểm của cạnh SA và cạnh CD.
1) Tìm giao tuyến d của mặt phẳng (SAD) và mặt phẳng (MOP) (0,75 điểm) Câu 5 M   MOP 
 M MOP SAD (1) 0,25 M  S , A SA   SAD  M SAD AD/ / OP 
Có OP  MOP 2 0,25 AD   SAD
Từ (1) và (2) suy ra giao tuyến d là đường thẳng đi qua điểm M và d // AD // 0,25 OP Tìm giao tuyến của mặt phẳng (SAC) và (SBD). (0,75 điểm)
S SAC SBD 3, trong mp (ABCD) O là giao điểm của AC và BD 0,25 O
  AC, AC  SAC  O  SAC 
 O SAC SBD 4 0,25 O   BD,BD   SBD  OSBD
Từ (3) và (4) suy ra SO là giao tuyến của (SAC) và (SBD) 0,25
2) Tìm giao điểm Q của đường thẳng AB và mặt phẳng (MOP). (0,75 điểm)
Gọi Q là giao điểm của OP và AB trong mặt phẳng (ABCD) 0,25 Q   AB  Q  OP,OP   MOP  QMOP 0,25
Suy ra Q là giao điểm của AB và mp (MOP) 0,25 Vẽ nối hình đầy đủ
3) Gọi K là giao điểm của đường thẳng DQ và đường thẳng AC, G là trọng tâm của tam giác SAD. Chứng minh KG // (SBC). ( 1,0 điểm)     DK 2   Có K DQ AO K là trọng tâm của ABD (5) DQ 3 0,25   DG 2  G là trọng tâm của SAD DM 3 0,25 (6)  DG DK MDQ có 
 GK / /MQ mà MQ / /SB .... .  KG / /SB 0 , 2 5 DM DQ KG / /SB 
Ta có SB  SBC   KG / /SBC  0,25 KG   SBC
4) Dựng thiết diện của mặt phẳng (MOP) với hình chóp SABCD. ( 0,75 điểm)
Trong mặt phẳng (SAD), đường thẳng d cắt đường thẳng SD tại điểm N. Khi đó
MOPABCD  PQ  
MOP  SAD  MN  0,5 
  thiết diện cần tìm là tứ giác MNPQ
MOP  SAB  MQ  MOP SDC NP     MN / /OP  MN / /PQ 0,25
Vậy thiết diện MNPQ là hình thang.
NỘI DUNG KIỂM TRA HKI MÔN TOÁN KHỐI 11 Thời gian: 90 phút Đại số: ( 6 điểm)
Phương trình lượng giác. ( 1,5 điểm)
Nhị thức Newton. ( 1,5 điểm)
Cấp số cộng- Cấp số nhân. ( 1,5 điểm) Xác suất. ( 1,5 điểm) Hình học: ( 4 điểm)
Tìm giao tuyến, giao điểm, thiết diện.
Chứng minh đường thẳng // mặt phẳng.
Chứng minh 3 điểm thẳng hàng, 3 đường thẳng đồng quy.