S Ở GIÁO DỤC VÀ ĐÀO TẠO TP.HCM ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2019-2020
TRƯỜNG THPT LÝ THÁI TỔ MÔN : TOÁN – KHỐI 11 THỜI GIAN: 90 PHÚT
(Không kể thời gian phát đề)
Họ và tên:…………………………………. Số báo danh:………………….. Lớp 11……….
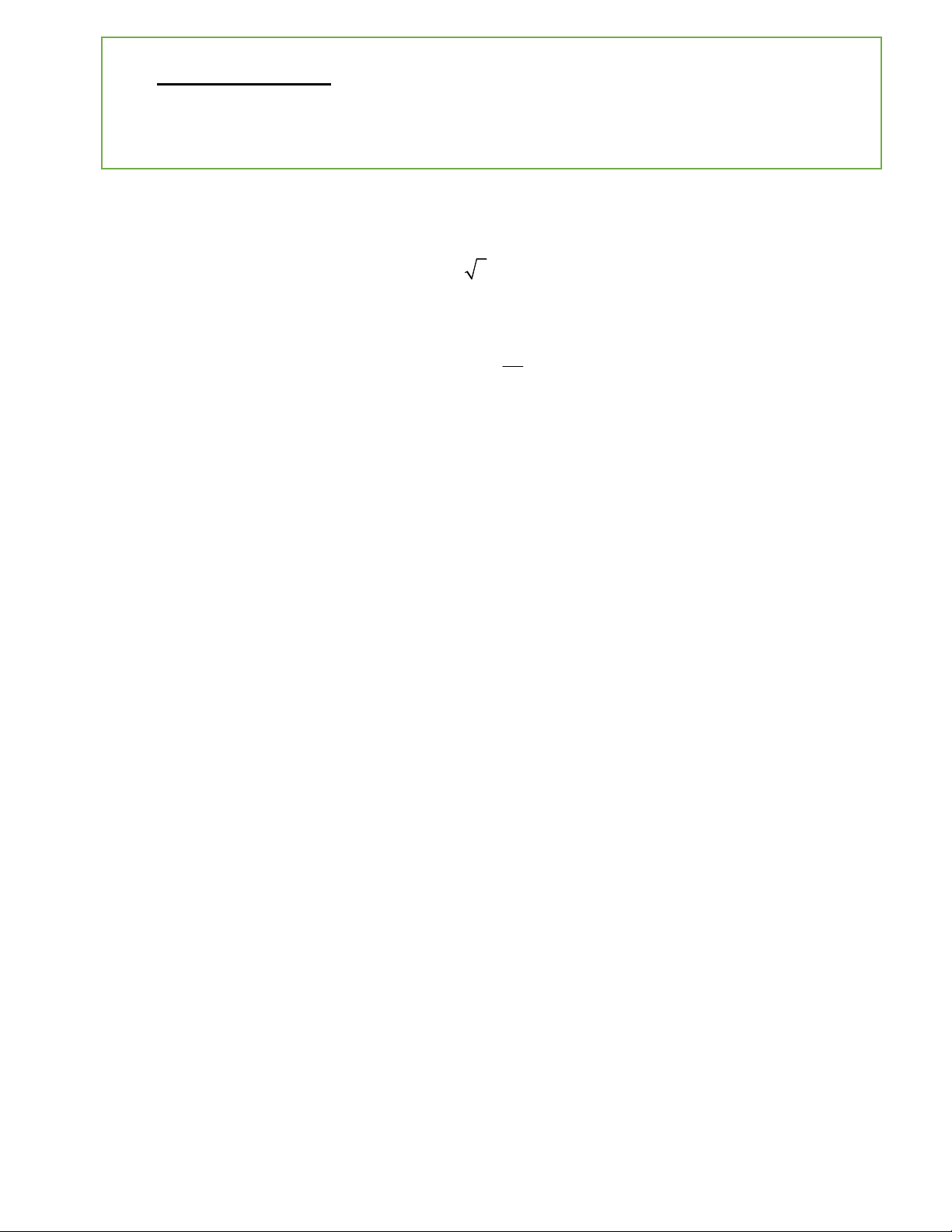
Câu 1: (1đ) Giải phương trình: 2 a) 2sin x  cos x 1  0
b) 3 sin x  cos x  2sin 2x
Câu 2: (1đ) Giải phương trình: 3 x2 A  C  14x . x x 6  2 
Câu 3: (1đ) Tìm hệ số chứa 3 x trong khai triển x   . 2 x   
Câu 4: (1đ) Tìm n biết hệ số của x3 trong khai triển (1 – 5x)n bằng -20625
Câu 5: (1đ) Một hộp có 10 viên bi xanh, 5 viên bi đỏ, 6 viên bi vàng. Chọn ngẫu nhiên 4 viên bi.
Tính xác suất để 4 viên bi được chọn có cùng màu.
Câu 6: (1đ) Từ tập X  0,1,2,3,4,5,6,7,8, 
9 , có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số
khác nhau mà số đó là số lẻ.
Câu 7: (1đ) Hãy tìm số hạng đầu, công sai, số hạng thứ 15 và tổng của 20 số hạng đầu S của 20  u  u  u  10 cấp số cộng sau: 1 5 3  . u  u  17 1 6
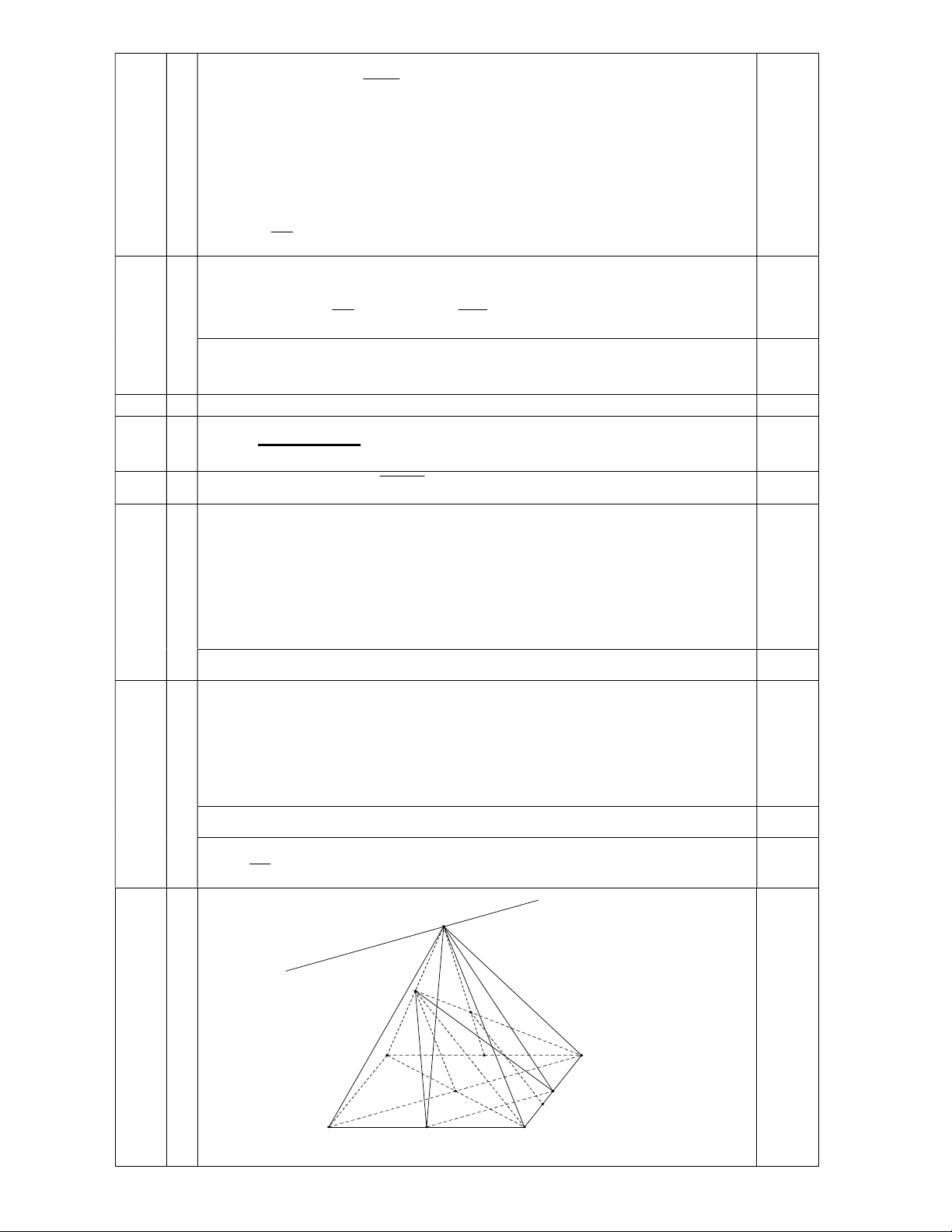
Câu 8: (3đ) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, P lần lượt
là trung điểm của BC, CD, SA.
a) Tìm giao tuyến SMN SBD .
b) Chứng minh: SC / / PBD.
c) Gọi G là trọng tâm SAD , lấy điểm E thuộc cạnh CD sao cho 3DE  2DC . Chứng minh rằng: GE / / SAC. ……HẾT……
(Giám thị coi thi không giải thích gì thêm)
ĐÁP ÁN THANG ĐIỂM MÔN TOÁN 11 Câu Ý Nội dung Điểm 1 a 2
2sin x  cos x 1  0  2 2
1  cos x  cos x 1  0 2
  2cos x  cos x 1  0 0,25 cos x  1   1  cos x   2
cos x  1  x  k2 k  Z 1  2 cos x   cos x  cos 0,25 2 3 2  x    k2 k  Z 3 b 3 1
3 sin x  cos x  2sin 2x  sin x  cos x  sin 2x 2 2 0,25     
 cos sin x  sin cos x  sin 2x  sin x   sin 2x   6 6  6      x   2x  k2 x    k2  6  6     0,25   5   x     2x  k2 3x   k2  6  6   x   k2  6   k Z 5   k2 x    18 3 2 x  3 3 x2 A  C  14x dk : x x  x  N 0,25 x! x! Pt        x    x  x   14x x 3 ! 2 !. 2 ! x  x  
1  x  2 x  3! x x   1  x  2!        x   14x x 3 ! 2 2 ! 0,25 
 x x  x   xx  1 1 2  14x  0 2   
 x x  x   x 1 1 2  14  0 2    x  0  1      x  x   x 1 1 2  14  02 0,25   2  1: x  0l     x   x   x 1 2 : 1 2  14  0 2 0,25  2 2
x  3x  2  x 1 28  0 2  2x  5x  25  0 x  5n   5  x  l  2 3 Số hạng tổng quát: k k k 6k  2  k 6k 2 k k 6k 2  k k k 63 T     0,5  C .x .  C .x . C .2 .x .x C .2 . k x k 1 6 2 6 2k 6 6  x  x Số hạng chứa 3
x tương ứng: 6  3k  3  k  1 0,5
Vậy hệ số cần tìm: 1 1 C .2  12 6 4 C = 165 <=> n = 11 1,0 5 1,0 P(A) = 6
Gọi số cần tìm có dạng: abcde a  b  c  d  e 0,25 e :5 cc  a :8 cc  0,5 b :8 cc c :7 cc  d :6 cc 
Vậy số cách chọn thỏa YCBT: 5.8.8.7.6  13440 cc 0,25 7 u  u  u  10
u  u  4d  u  2d  10 1 5 3 1 1  1     u  u  17 u  u  5d  17 1 6 1 1 0,5 u  2d  10 u  16 1 1     2  u  5d  17 d  3 1 u  u 14d  16 14. 3   26 0,25 15 1   20 0,25 S 
2u 19d  10 2.16 19. 3   250 20  1     2  8 S 0,5 x P G A D I O N E B M C a SMNSBD 0,5 M trung ®iÓm BC Xét BCD , có:  N trung ®iÓm CD
 MN là đường trung bình trong BCD  MN / / BD S SMN SBD  BD  SBD 0,5 Ta có: 
 SMN SBD  Sx / /MN / / BD MN  SMN  BD / / MN b SC / / PBD P trung ®iÓm SA Xét SAC , có:  0,5
O trung ®iÓm AC (ABCD lµ h×nh b×nh hµnh)
 PO là đường trung bình trong SAC  PO / /SC SC / /PO 
Ta có: PO  PBD  SC / / PBD 0,5 SC   PBD c DG 2
Ta có G là trọng tâm SAD     1 DP 3 0,25 DE 2 Mặt khác: 3DE  2DC   2 DC 3   DG DE 1 ,2   DP DC DG DE Xét DPC , có:  DP DC
 GE / /PC ( Định lý Tallet đảo) Ta có: GE / /PC  0,25
PC  SAC  GE / / SAC GE   SAC