


Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2019 -2020 TP HỒ CHÍ MINH
MÔN: TOÁN - Khối 11
TRƯỜNG THPT NGUYỄN CHÍ THANH
Thời gian làm bài 90 phút
(Không tính thời gian phát đề ) ĐỀ CHÍNH THỨC
Bài 1: (2,0 điểm) Giải các phương trình : a.
3 cos x sin x 2 2
b. 1 sin x cos x 1 sin x 2 sin x
Bài 2: (1,0 điểm) Trong khai triển 15 2 xy x
hãy tìm số hạng có số mũ của x bằng bình phương số mũ của y.
Bài 3: (1,0 điểm) Một câu lạc bộ văn nghệ có 4 nam và 5 nữ. Nhà trường muốn chọn 4 em tam
gia một tốp ca. Tính xác suất để tốp ca có cả nam lẫn nữ.
2u u 3
Bài 4: (1,0 điểm) Cho cấp số cộng u biết 1 4
. Tìm u , d và công thức số hạng n S 96 1 12
tổng quát của cấp số cộng đó.
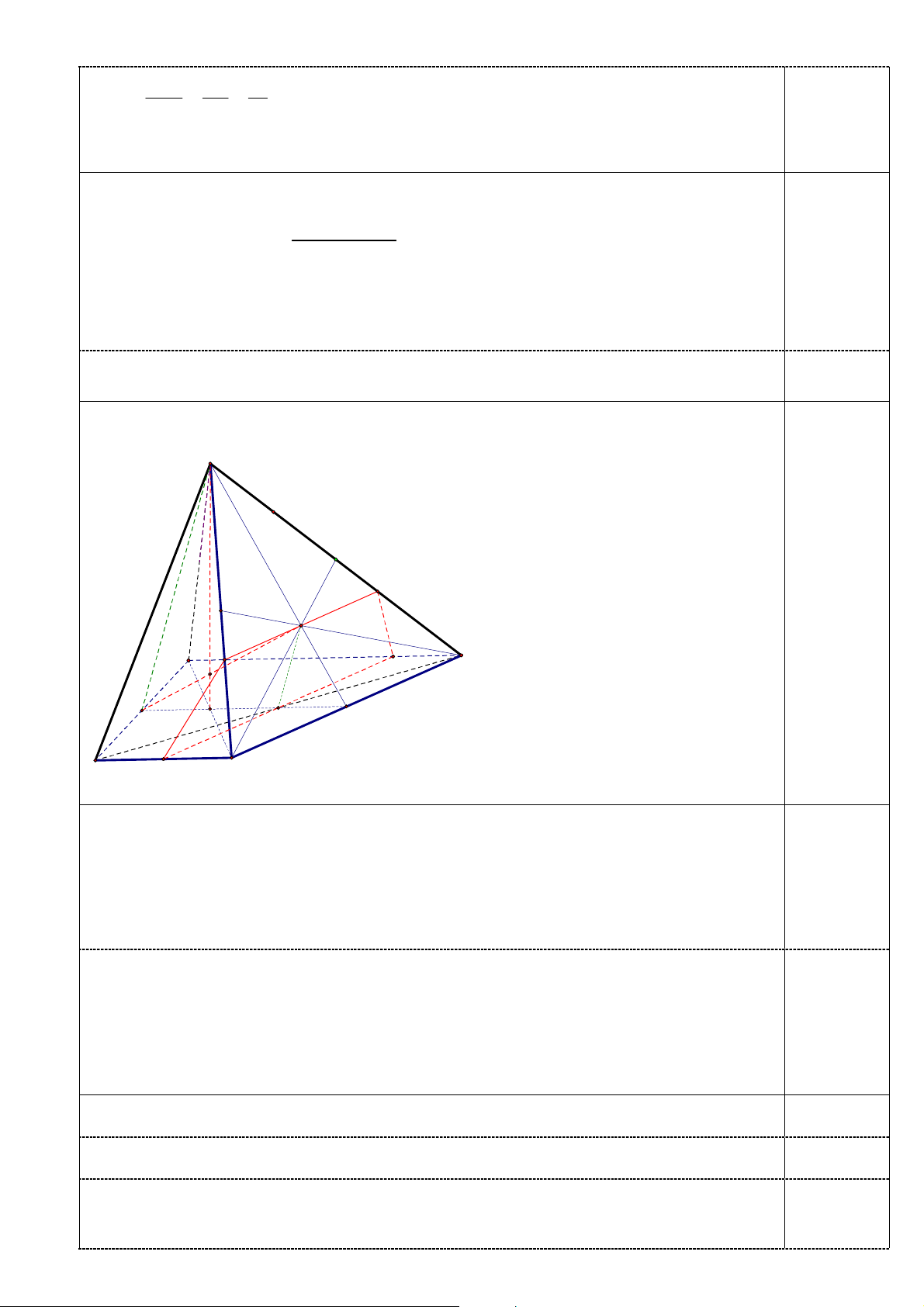
Bài 5: (4,0 điểm) Cho hình chóp S.ABCD có ABCD là hình thang đáy lớn AB, biết
AB 2CD . Gọi G là trọng tâm của tam giác SBC và E, F lần lượt là trung điểm của các cạnh BC, AD
1) Tìm giao tuyến của các mặt phẳng: (SAB) với (SCD) và (SAD) với (SBC)
2) Tìm giao điểm K của GF với (SAC)
3) I là giao điểm của BD với EF. Chứng minh: GI song song với (SAD).
4) () là mặt phẳng qua GI và song song với BC. Tìm thiết diện của () với hình chóp S.ABCD
Bài 6: (1,0 điểm) Tính giá trị biểu thức sau theo số tự nhiên n: S 1 11 111 ... 11 ... ...1 n soá 1 ------- HẾT -------
ĐÁP ÁN TOÁN K11 – HỌC KỲ 1 – 2019-2020
Bài 1 (2 điểm) Giải các phương trình sau :
a/ 3 cos x sin x 2 3 1 0,25+0,25 cos x sin x 1 sin( x) 1 2 2 3 x
k 2 x
k 2 , k Z 0,25+0,25 3 2 6 2
b/ 1 sin x cos x1 sin x 2 sin x 2
1 2 sin x sin x cos x sin x.cos x 2 sin x 2
sin x cos x sin x cos x sin x 1 0 0,25 2
sin x cos x sin x.cos x cos x 0
sin x cos x cos x sin x cos x 0
sin x cos x1 cos x 0 0,25 sin x cos x 0 x k 0,25+0,25 4 k cos x 1 x k2 Bài 2 ( 1 điểm ) 15 15 15k Ta có: x xy C x xyk 2 k 2 . 15 k0
Số hạng tổng quát là: k 30k k 0,25 k T +1 1 C 5x y
(HS chỉ cần viết được 1 trong 2 là được)
Số mũ của x bằng bình phương số mũ của y nên 2 30 – k k 0,25 k 6 (l) 0,25 k 5 (n)
Vậy số hạng cần tìm là 5 25 5 25 5 C x y 3003x y 0,25 15
Bài 3 ( 1 điểm ) ta có : nΩ 4 C 126 0,25 9
Gọi A là biến cố : ‘chọn 4 học sinh có cả nam và nữ ‘
TH1: chọn 1 nam và 3 nữ: 1 3 C .C 40 4 5
TH2: chọn 2 nam và 2 nữ: 2 2 C .C 60 4 5
TH3: chọn 3 nam và 1 nữ: 3 1 0,5 C .C 20 4 5
(HS làm được 2 trường hợp thì cho 0,25)
nA 40 60 20 120 . n 0,25 p A 120 20 A nΩ 126 21
HS có thể sử dụng biến cố đối hoặc cách giải khác để giải 3u 3d 3 0,25 2u u 1 3 1 4 Bài 4: 122u 11d 0,25 1 S 96 12 96 2 u 3 0,25 1 d 2
Suy ra công thức số hạng tổng quát của cấp số cộng u 3 2 n 1 2n 5 0,25 n Bài 5(4đ) S Q G P A M K B F I J E D N C Bài 5:
S (SAB) (SCD) 0,25 1)
AB/ / CD, AB (SAB), CD (SCD)
Suy ra (SAB) (SCD) x 'Sx, x'Sx/ / AB/ / CD 0,25
Ta có: S (SAD) (SBC)
O AD, AD (SAD) 0,25 Trong mp(ABCD), gọi
O AD BC
O (SAD) (SBC)
O BC, BC (SBC)
Suy ra: SO (SAD) (SBC) 0,25
2). Trên (ABCD), gọi J = AC EF 0,25
Trên (SEF) gọi FG SJ = K 0,25 K FG 0,25
K SJ , SJ (SAC) K = FG (SAC) 0,25
3) I là giao điểm của BD với EF. Chứng minh : GI song song với (SAD). EG 1 0,25
Ta có: G là trọng tâm SBC ES 3 EI 1 0,25 Chứng minh được EF 3 EI 1 EF EI EG Xét tam giác SEF có 3 IG // SF EG 1 EF ES 0,25 ES 3 IG / /SF 0,25
SF SAD IG / / SAD
IG SAD 4).
I ABCD 0,25 / /BC
ABCD MN , MN qua I và MN // BC,
BC ABCD
M AB, N CD
G SBC 0,25 / /BC
SBC PQ , PQ qua G và PQ // BC, Q SB, P SC
BC SBC
() (SAB) = MQ và () (SCD) = NP 0,25
Kết luận thiết diện MNPQ là hình thang 0,25
Bài 6: Tính giá trị của biểu thức sau theo số tự nhiên n: S 111 111 ... 11......1 n soá 1 Ta có: 2
9 9 99 .... 99...9 10 10 ... 10n S n 0,25+0,25 1010n n 1 10 1 n 0,25+0,25 9S 10
n S 101 81 9




