SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM
ĐỀ KIỂM TRA HỌC KỲ I
TRƯỜNG THPT HOÀNG HOA THÁM Năm học : 2019 – 2020 Môn : TOÁN – Lớp 11
Thời gian làm bài : 90 phút, không kể thời gian phát đề. x x
Câu 1 (1.0 điểm). Giải phương trình: 2 cot
 1 3cot  3  0. 2 2
Câu 2 (1.0 điểm). Giải phương trình:  3   1 sin x   3   1 cos x  3 1  0
Câu 3 (1.0 điểm). Cho tập A  1;2;3;4;5;6;7;8; 
9 . Từ tập A có thể lập được bao nhiêu số tự nhiên lẻ
có năm chữ số khác nhau và không chia hết cho 5. 12  1 
Câu 4 (1.0 điểm). Tìm số hạng không chứa x trong khai triển 2 2x  .    x 
Câu 5 (1.0 điểm). Đội tuyển Toán lớp 11 của trường Hoàng Hoa Thám gồm 7 bạn lớp 11A1, 5 bạn lớp
11A2 và 3 bạn lớp 11A3. Chọn ngẫu nhiên 4 bạn để đi thi kì thi Olympic 30/4, tính xác suất để 4 bạn
được chọn có đủ cả 3 lớp. 6n  4
Câu 6 (1.0 điểm). Xét tính tăng giảm của dãy số u biết u  ,  n  n  . n  n  2 u  u  2 
Câu 7 (1.0 điểm). Tìm số hạng đầu và công sai của cấp số cộng biết: 3 8  2 2 u  u  68  1 6
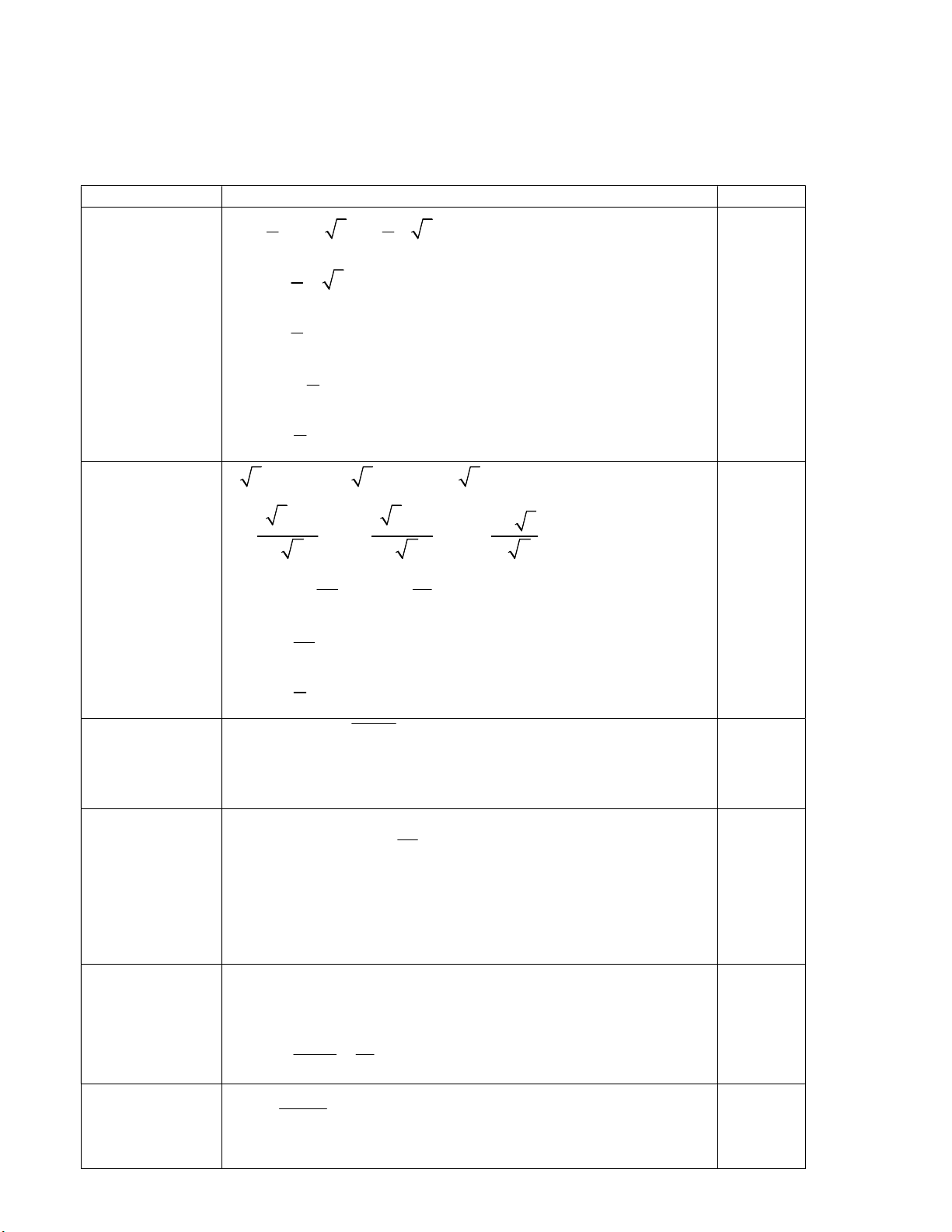
Câu 8 (1.0 điểm). Cho hình chóp S.ABCD với ABCD là hình thang đáy lớn A . D M là điểm thuộc đoạn thẳng S .
A Xác định giao điểm I của đường thẳng SD và mặt phẳng MBC .
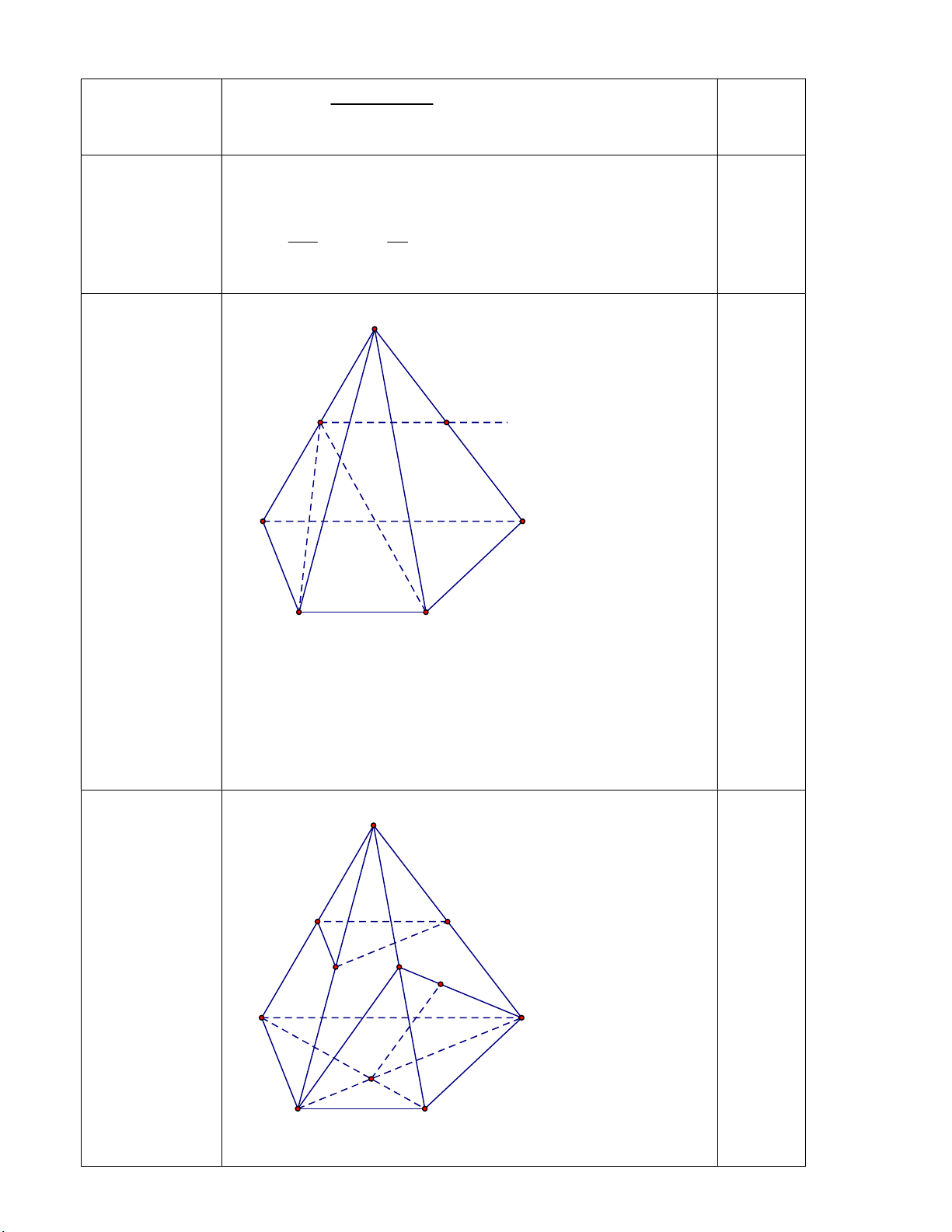
Câu 9 (2.0 điểm). Cho hình chóp S.ABCD có ABCD là hình thang, AD / /BC và AD  2.BC . Gọi
M, N, P lần lượt là trung điểm SA, SB, SD; G là trọng tâm tam giác SCD và O  AC  BD.
a) Chứng minh: MNP / / ABCD.
b) Chứng minh: OG / / SBC. --- HẾT ---
Thí sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm.
Họ, tên thí sinh:……………………………………………………………..Số báo danh:………………… Đáp án Toán 11 – HKI Câu Lời giải Điểm Câu 1 x x 2 cot  1 3 (1 điểm) cot  3  0 2 2  x 0,25 cot  3  0,25 2   x cot 1  2   0,25 x    k2  0,25 2    x   k2  3 Câu 2
 3 1sinx 3 1cosx 31 0 (1 điểm)  3 1  3 1 1 3  sin x  cos x  0,25 2 2 2 2 2 2  5      0,25 sin x   sin       12   12   3 x   k2  0,25 2   0,25  x   k2  3 Câu 3
Gọi số cần tìm là abcde (1 điểm) Số cách chọn e: 4 cách 0,25
Số cách chọn a, b, c, d: 8.7.6.5 0,5 Vậy có 6720 số. 0,25 Câu 4   0,25 k  1 k k  (1 điểm) SHTQ :C 2x 12 2 . 12    x  0,25 12  .2   k k k 243 1 . k C x 0,25 12
Số hạng không chứa x : 24  3k  0  k  8
Vậy số hạng không chứa x là 7920. 0,25 Câu 5 n  4  C  1365 0,25 (1 điểm) 15 0,5 n A 1 1 2 1 2 1 2 1 1
 C C C  C C C  C C C  630 7 5 3 7 5 3 7 5 3 P  A n A 6   n  13 0,25 Câu 6 6n  2 0,25 (1 điểm) u  n 1  n  3 0,5 16 u  u   0, n   * n 1  n n  2n3 0,25 Dãy số tăng. Câu 7
u  u  2  2u  9d  2 0,25 3 8 1 (1 điểm)  0,25
u 2  u  5d 2  68 1 1 338 66  0,25 u   d   1 41 41 Hay u  8   d  2 0,25 1 Câu 8 (1 điểm) S M I x A D B C M SAD MBC 0,25 AD / /BC 0,25
 SAD MBC  Mx / / AD / /BC 0.25  Mx  SD  I  SD MBC  I 0,25 Câu 9 (2 điểm) S M P N I G A D O B C
a) Chứng minh MNP / / SAB 0,25 0,25 MN / / AB MP / / AD MN  MP  M 0,5 Vậy MNP / / SAB
b) Chứng minh OG / / SBC
Gọi E là trung điểm của SC. OD AD 2 BC / / AD    0,25 OB BC 1 DO 2   DB 3 DG 2 0,25
 (G là trọng tâm của tam giác SCD) DE 3 0,25 DO DG 2    nên OG / /BE DB DE 3 0,25 BE  SBC Vậy OG / / SBC .