Đề thi học kì 1 Toán 11 năm 2019 – 2020 trường THPT Bà Điểm – TP HCM

Kỳ thi cuối học kì 1 môn Toán 11 là kỳ thi rất quan trọng đối với các em học sinh lớp 11, điểm số của kỳ thi này tác động lớn đến điểm trung bình môn Toán 11 nói riêng và xếp loại học lực nói chung.

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 11

Môn: Toán 11

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT BÀ ĐIỂM
(Đ
ề
thi g
ồ
m 01 trang)
ĐỀ KIỂM TRA HỌC KỲ I – NH: 2019-2020
MÔN TOÁN – LỚP 11 (14.12.2019)
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
Họ tên học sinh: ………………..…………………, Lớp: ………, Số báo danh: ……………….......
Câu 1: (3.0 điểm) Giải các phương trình sau:
a)
sin 2 cos6 0
x x
b)
2 2
4cos 2 4 3 sin 2 cos2 2sin 2
2
x x x x
c)
1 cos 2 cos 1 2 cos 3 sin
x x x x
Câu 2: (1.0 điểm) Giải phương trình:
2 2
2
2 50
x x
A A
Câu 3: (1.0 điểm) Bạn Danh viết ngẫu nhiên lên bảng 4 số tự nhiên khác nhau thuộc [1;19]. Tính xác suất để
bốn số được viết ra có tổng là một số chẵn.
Câu 4: (1.0 điểm) Một cấp số cộng có 10 số hạng. Biết rằng tổng số hạng đầu và số hạng cuối bằng 30, tổng số
hạng thứ ba và thứ sáu bằng 35. Số hạng thứ bảy của cấp số cộng là bao nhiêu.
Câu 5: (2.0 điểm) Cho hình chóp S.ABC, gọi M,N lần lượt là trọng tâm của SAB, SBC. Gọi I là trung điểm
của AC.
a) Xác định giao tuyến của (BMN) và (SAC).
b) Tìm giao điểm J của đường thẳng SB và mặt phẳng (IMN).
Câu 6: (2.0 điểm) Cho hình chóp S.ABCD có đáy là hình bình hành .Hai điểm M, N lần lượt là trung điểm của
AB, BC.
a) Chứng minh rằng MN song song mặt phẳng (SAC).
b) Điểm E nằm trên cạnh SD ( điểm E không trùng với hai điểm S và D). Xác định thiết diện cắt bởi mặt phẳng
(MNE) và hình chóp S.ABCD.
HẾT
ĐÁP ÁN VÀ THANG ĐIỂM MÔN TOÁN 11
CÂU ĐÁP ÁN
ĐIỂM
1
(3.0đ)
Câu 1: (3.0 điểm) Giải các phương trình sau:
a)
sin 2 cos6 0
x x
sin 2 cos6 0
x x
sin 2 sin( 6 )
2
x x
0.5
16 4
( )
8 2
k
x
k
k
x
0.5
b)
2 2
4cos 2 4 3 sin 2 cos2 2sin 2
2
x x x x
cos2 0
4 2
x x k k
thì
5
pt 2
2
(sai)
4 2
x k
không là nghiệm của phương trình.
0.25
cos2 0
4 2
x x k k
2 2
5
4 4 3 tan 2 2 tan 2 1 tan 2
2
pt x x x
0.25
2
9 3
tan 2 4 3 tan 2 0
2 2
x x
tan 2 3
3
tan 2
9
x
x
0.25
6 2
1 3
arctan
2 9 2
x k
k
x k
0.25
c)
1 cos 2 cos 1 2 cos 3 sin
x x x x
2
1 cos 2 cos 1 2cos 3 sin 1 cos 2 cos 2cos 3 sinx
cos 3 sinx 2cos 2 cos cos 2
3
x x x x x x x
x x x x
0.5
2
3
;k
2
9 3
x k
k
x
0.5
2
Câu 2: (1.0 điểm) Giải phương trình:
2 2
2
2 50
x x
A A
K
J
H
N'
M'
F
E
I
N
M
C
B
A
S
(1.0đ)
Điều kiện:
, 2
x x
0.25
2 2
2
2 50
x x
A A
! (2 )!
2 50
( 2)! (2 2)!
x x
x x
0.25
2 ( 1) 50 2 (2 1)
x x x x
0.25
2
5( )
4 50 0
5( )
x N
x
x L
0.25
3.
(1.0đ)
Câu 3: (1.0 điểm) Bạn Danh viết ngẫu nhiên lên bảng 4 số tự nhiên khác nhau thuộc [1;19].
Tính xác su
ấ
t đ
ể
b
ố
n s
ố
đư
ợ
c vi
ế
t ra có t
ổ
ng là m
ộ
t s
ố
ch
ẵ
n.
4
19
3876
n C
0.5
Gọi A là biến cố thỏa đề bài.
Có 10 số lẻ và 9 số chẵn
4 2 2 4
9 9 10 10
. 1956
n A C C C C
0.25
163
323
P A
0.25
4.
(1.0đ)
Câu 4: (1.0 điểm) Một cấp số cộng có 10 số hạng. Biết rằng tổng số hạng đầu và số hạng cuối bằng 30,
tổng số hạng thứ ba và thứ sáu bằng 35. Số hạng thứ bảy của cấp số cộng là bao nhiêu.
Ta có:
1 10
3 6
30
35
u u
u u
0.25
1
1
2 9 30
2 7 35
u d
u d
0.25
1
105
4
5
2
u
d
0.25
7 1
45
6
4
u u d
0.25
5.
(2.0đ)
Câu 5: (2.0 điểm) Cho hình chóp S.ABC, gọi M,N lần lượt là trọng tâm của SAB, SBC. Gọi I là
trung điểm của AC.
a) Xác định giao tuyến của (BMN) và (SAC).
Gọi E, F lần lượt là trung điểm SA,SC.
, ( )
, ( )
( ) ( ) (1)
E BM BM BMN
E SA SA SAC
E BMN SAC
0.5
, ( )
, ( )
( ) ( ) (2)
F BN BN BMN
E SC SC SAC
F BMN SAC
0.25
(1);(2) ( ) ( ) EF
BMN SAC
0.25
b) Tìm giao
đi
ể
m J c
ủ
a đư
ờ
ng th
ẳ
ng SB và m
ặ
t ph
ẳ
ng (IMN).
Gọi M’,N’ lần lượt là trung điểm AB,BC.
Trong (ABC) g
ọ
i H=BI
M’N’
0.25
Trong (SM’N’) gọi K=MNSH
0.25
Trong (SBI):Gọi J=SBIK
0.25
, ( )
( )
J SB
J IK IK IMN
J SB IMN
0.25
6
(2.0đ)
Câu 6: (2.0 điểm) Cho hình chóp S.ABCD có đáy là hình bình hành .Hai điểm M, N lần lượt là trung
điểm của AB, BC.
a) Ch
ứ
ng minh r
ằ
ng MN song song
m
ặ
t ph
ẳ
ng (SAC).
/ / ABC
MN AC MN
MN SAC
AC SAC
laø ñöôøng trung bình cuûa
0.75
/ /
MN SAC
0.25
b) Điểm E nằm trên cạnh SD ( điểm E không trùng
với hai điểm S và D). Xác định thiết diện cắt bởi mặt
ph
ẳng (MNE) v
à hình chóp S.ABCD.
Q
P
A
D
B
C
S
J
M
N
E
I
Trong
: ,
ABCD I MN CD J MN AD
0.25
Trong
:
SCD P IE SC
Trong
:
SAD Q JE SA
0.25
MNE ABCD MN
MNE SBC NP
MNE SCD PE
MNE SAD EQ
MNE SAB QM
0.25
V
ậ
y thi
ế
t di
ệ
n c
ắ
t b
ở
i (MNE) và S.ABCD là ng
ũ giác MNPEQ
0.25
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ I – NH: 2019-2020 THÀNH PHỐ HỒ CHÍ MINH
MÔN TOÁN – LỚP 11 (14.12.2019) TRƯỜNG THPT BÀ ĐIỂM
Thời gian làm bài: 90 phút (không kể thời gian phát đề) (Đề thi gồm 01 trang)
Họ tên học sinh: ………………..…………………, Lớp: ………, Số báo danh: ……………….......
Câu 1: (3.0 điểm) Giải các phương trình sau: a) sin 2x  cos 6x  0 5 b) 2 2
4cos 2x  4 3 sin 2x cos 2x  2sin 2x  2
c) 1 cos 2x  cos x 1 2cos x  3 sin x
Câu 2: (1.0 điểm) Giải phương trình: 2 2 2A  50  A x 2 x
Câu 3: (1.0 điểm) Bạn Danh viết ngẫu nhiên lên bảng 4 số tự nhiên khác nhau thuộc [1;19]. Tính xác suất để
bốn số được viết ra có tổng là một số chẵn.
Câu 4: (1.0 điểm) Một cấp số cộng có 10 số hạng. Biết rằng tổng số hạng đầu và số hạng cuối bằng 30, tổng số
hạng thứ ba và thứ sáu bằng 35. Số hạng thứ bảy của cấp số cộng là bao nhiêu.
Câu 5: (2.0 điểm) Cho hình chóp S.ABC, gọi M,N lần lượt là trọng tâm của SAB, SBC. Gọi I là trung điểm của AC.
a) Xác định giao tuyến của (BMN) và (SAC).
b) Tìm giao điểm J của đường thẳng SB và mặt phẳng (IMN).
Câu 6: (2.0 điểm) Cho hình chóp S.ABCD có đáy là hình bình hành .Hai điểm M, N lần lượt là trung điểm của AB, BC.
a) Chứng minh rằng MN song song mặt phẳng (SAC).
b) Điểm E nằm trên cạnh SD ( điểm E không trùng với hai điểm S và D). Xác định thiết diện cắt bởi mặt phẳng (MNE) và hình chóp S.ABCD. HẾT
ĐÁP ÁN VÀ THANG ĐIỂM MÔN TOÁN 11 CÂU ĐÁP ÁN ĐIỂM 1
Câu 1: (3.0 điểm) Giải các phương trình sau: a) sin 2x  cos 6x  0 (3.0đ) 
sin 2x  cos 6x  0  sin 2x  sin(  6x) 2 0.5   k x    16 4   (k  )  k 0.5 x     8 2 5 b) 2 2
4cos 2x  4 3 sin 2x cos 2x  2sin 2x  2   5 0.25 cos 2x  0  x 
 k k  thì pt  2  (sai) 4 2 2  
 x   k không là nghiệm của phương trình. 4 2    cos 2x  0  x   k k  4 2 5 0.25 2
pt  4  4 3 tan 2x  2 tan 2x   2 1 tan 2x 2 tan 2x  3 0.25 9 3 2   
tan 2x  4 3 tan 2x   0  2 2  3 tan 2x    9    0.25 x   k  6 2   k   1  3   x  arctan      k 2  9  2   
c) 1 cos 2x  cos x 1 2 cos x  3 sin x  x  x   x 2 1 cos 2 cos 1 2cos
 3 sin x  1 cos 2x  cos x  2cos x  3 sinx 0.5   
 cos x  3 sinx  2cos 2x  cos  x  cos 2x    3    0.5 x   k2  3   ; k    k2 x    9 3 2
Câu 2: (1.0 điểm) Giải phương trình: 2 2 2A  50  A x 2 x
(1.0đ) Điều kiện: x  , x  2 0.25 x x 0.25 2 2 2A  50  ! (2 )! A  2  50  x 2 x (x  2)! (2x  2)!
 2x(x 1)  50  2x(2x 1) 0.25 x  5(N) 0.25 2  4x  50  0   x  5(L) 3.
Câu 3: (1.0 điểm) Bạn Danh viết ngẫu nhiên lên bảng 4 số tự nhiên khác nhau thuộc [1;19].
Tính xác suất để bốn số được viết ra có tổng là một số chẵn. (1.0đ) n 4  C  3876 0.5 19
Gọi A là biến cố thỏa đề bài. 0.25
Có 10 số lẻ và 9 số chẵn n A 4 2 2 4  C  C .C  C 1956 9 9 10 10 0.25 P  A 163  323 4.
Câu 4: (1.0 điểm) Một cấp số cộng có 10 số hạng. Biết rằng tổng số hạng đầu và số hạng cuối bằng 30,
tổng số hạng thứ ba và thứ sáu bằng 35. Số hạng thứ bảy của cấp số cộng là bao nhiêu. (1.0đ) Ta có: u   u  30 0.25 1 10  u  u  35  3 6 2u  9d  30 0.25 1   2u  7d  35  1  105 0.25 u   1  4   5 d    2 45  0.25 u  u  6d  7 1 4 5.
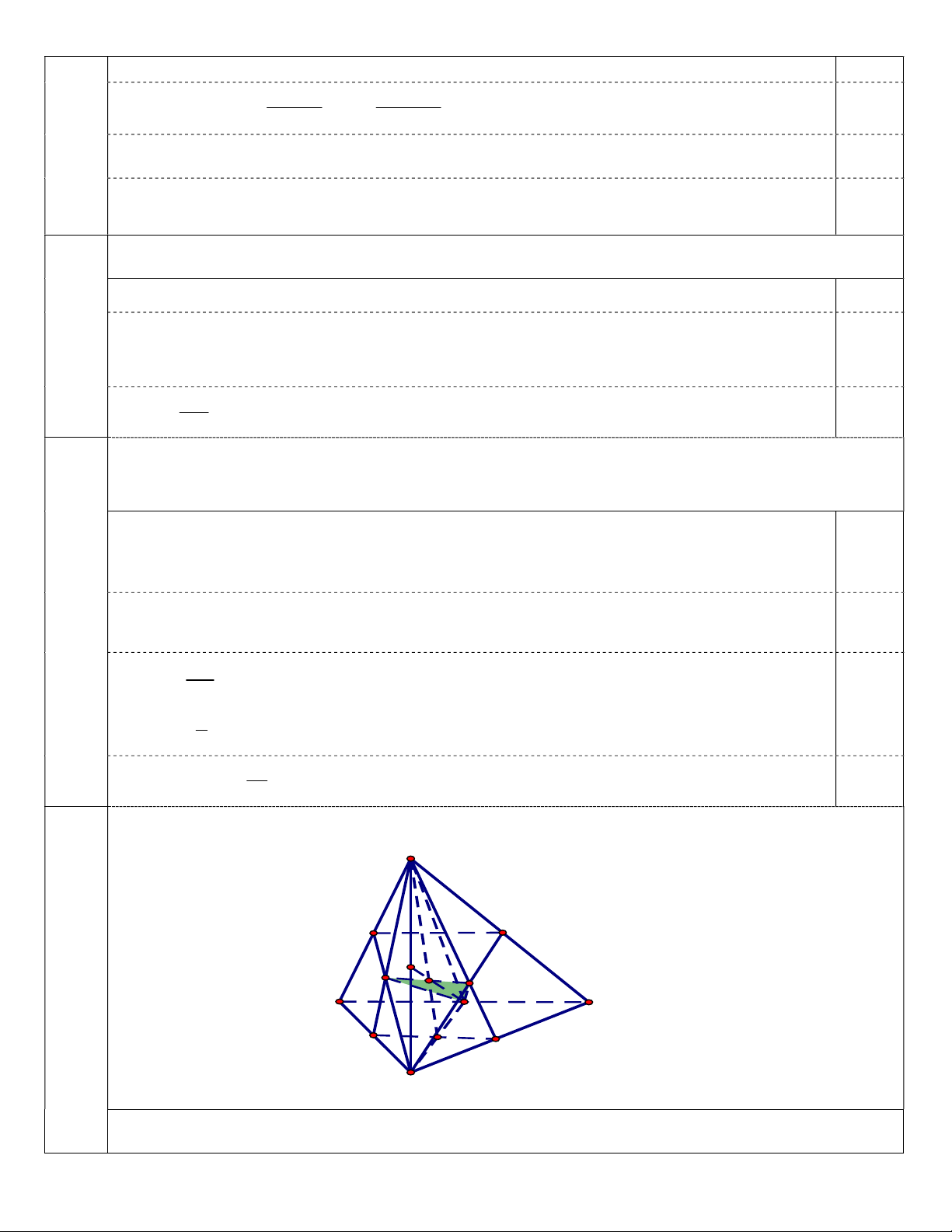
Câu 5: (2.0 điểm) Cho hình chóp S.ABC, gọi M,N lần lượt là trọng tâm của SAB, SBC. Gọi I là
(2.0đ) trung điểm của AC. S E F J K M N A I C H M' N' B
a) Xác định giao tuyến của (BMN) và (SAC).
Gọi E, F lần lượt là trung điểm SA,SC. 0.5 E  BM , BM  (BMN)  E  S , A SA  (SAC)  E  (BMN)  (SAC) (1) F  BN, BN  (BMN)  0.25 E  SC, SC  (SAC)  F  (BMN)  (SAC) (2)
(1);(2)  (BMN )  (SAC)  EF 0.25
b) Tìm giao điểm J của đường thẳng SB và mặt phẳng (IMN).
Gọi M’,N’ lần lượt là trung điểm AB,BC. 0.25
Trong (ABC) gọi H=BIM’N’
Trong (SM’N’) gọi K=MNSH 0.25 Trong (SBI):Gọi J=SBIK 0.25 J  SB 0.25  J  IK, IK  (IMN)  J  SB  (IMN) 6
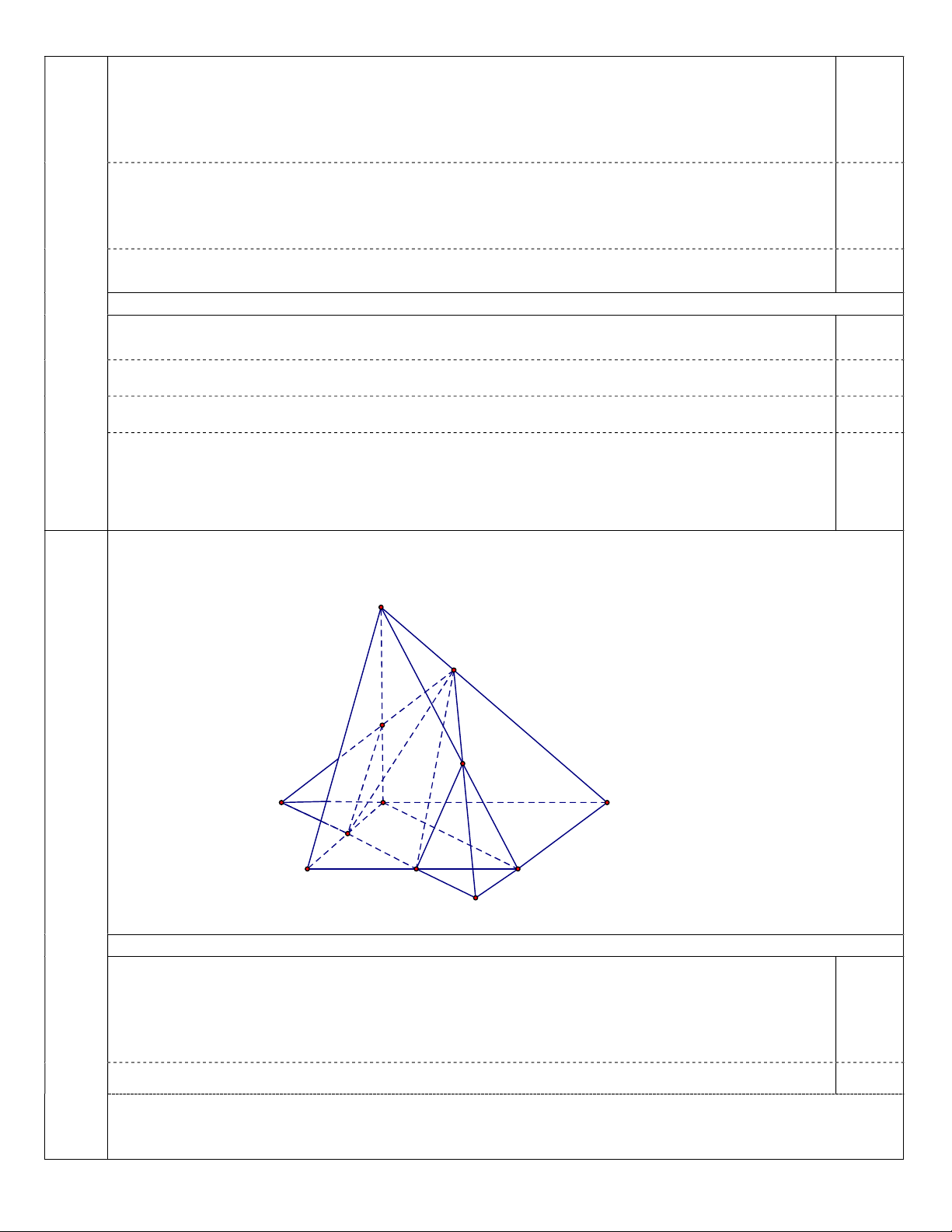
Câu 6: (2.0 điểm) Cho hình chóp S.ABCD có đáy là hình bình hành .Hai điểm M, N lần lượt là trung điểm của AB, BC. (2.0đ) S E Q P J D A M B N C I
a) Chứng minh rằng MN song song mặt phẳng (SAC).
MN / / AC MN laø ñöôøng trung bình cuûa A  BC 0.75  MN  SAC  AC   SAC  MN / / SAC 0.25
b) Điểm E nằm trên cạnh SD ( điểm E không trùng
với hai điểm S và D). Xác định thiết diện cắt bởi mặt
phẳng (MNE) và hình chóp S.ABCD.
Trong  ABCD : I  MN CD, J  MN  AD 0.25
Trong SCD : P  IE  SC 0.25
Trong SAD : Q  JE  SA MNE ABCD  MN 0.25 MNESBC  NP MNESCD  PE MNESAD  EQ MNESAB  QM
Vậy thiết diện cắt bởi (MNE) và S.ABCD là ngũ giác MNPEQ 0.25