
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ I
THÀNH PHỐ HỒ CHÍ MINH
NĂM HỌC 2019 – 2020
TRƯỜNG THPT HÀN THUYÊN
Môn: TOÁN – Khối 11
Thời gian làm bài: 90 phút (không tính thời gian phát đề). ĐỀ CHÍNH THỨC
Họ và tên học sinh: ………………………………………SBD – Mã số HS: ……………………...
Câu 1 (2,0 điểm).
Giải các phương trình lượng giác sau: π a) 2sin 3x + −1 = 0 4
b) 3 sin x − cos x =1 2
c) cot x − tan x + 4sin 2x = sin 2x
Câu 2 (3,0 điểm).
a) Cho tập X = {1; 2; 3; 4; 5}. Hỏi từ X lập được bao nhiêu số tự nhiên có hai chữ số đôi
một khác nhau và lớn hơn 30? 12
b) Tìm hệ số của số hạng chứa x12 trong khai triển của M = 2 1 x − . x
c) Một hộp chứa 4 quả cầu đỏ, 5 quả cầu xanh và 7 quả cầu vàng. Lấy ngẫu nhiên cùng lúc
4 quả cầu từ hộp đó. Tính xác suất để trong 4 quả cầu được lấy ra có đúng 1 quả cầu màu đỏ và
không quá 2 quả cầu màu vàng. Câu 3 (1,0 điểm). Cho cấp số cộng (u ) n có
. Hãy tìm tổng của 10 số hạng đầu tiên của cấp số cộng đó. Câu 4 (2,5 điểm).
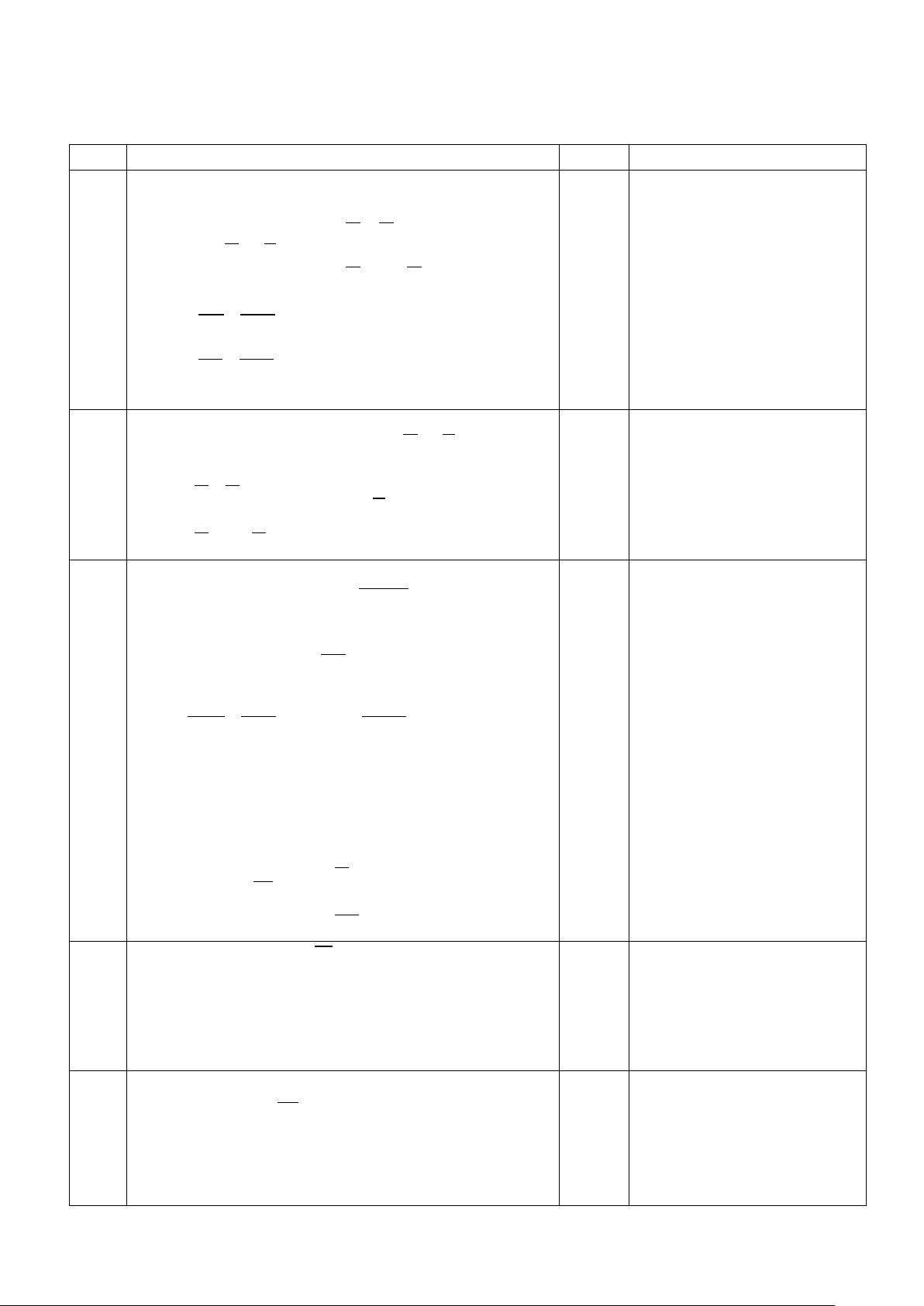
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N, K lần lượt là trung điểm AB, CD và SA.
a) Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD).
b) Tìm giao điểm của đường SD với mặt phẳng (MNK).
c) Chứng minh mặt phẳng (SBC) song song mặt phẳng (KMN). Câu 5 (1,5 điểm).
a) Trong mặt phẳng Oxy, cho hai điểm A(1; 3), B(3; 0) và đường thẳng có phương trình
(d): 3x – 2y + 1 = 0. Tìm ảnh (d’) của (d) qua phép tịnh tiến theo véctơ AB .
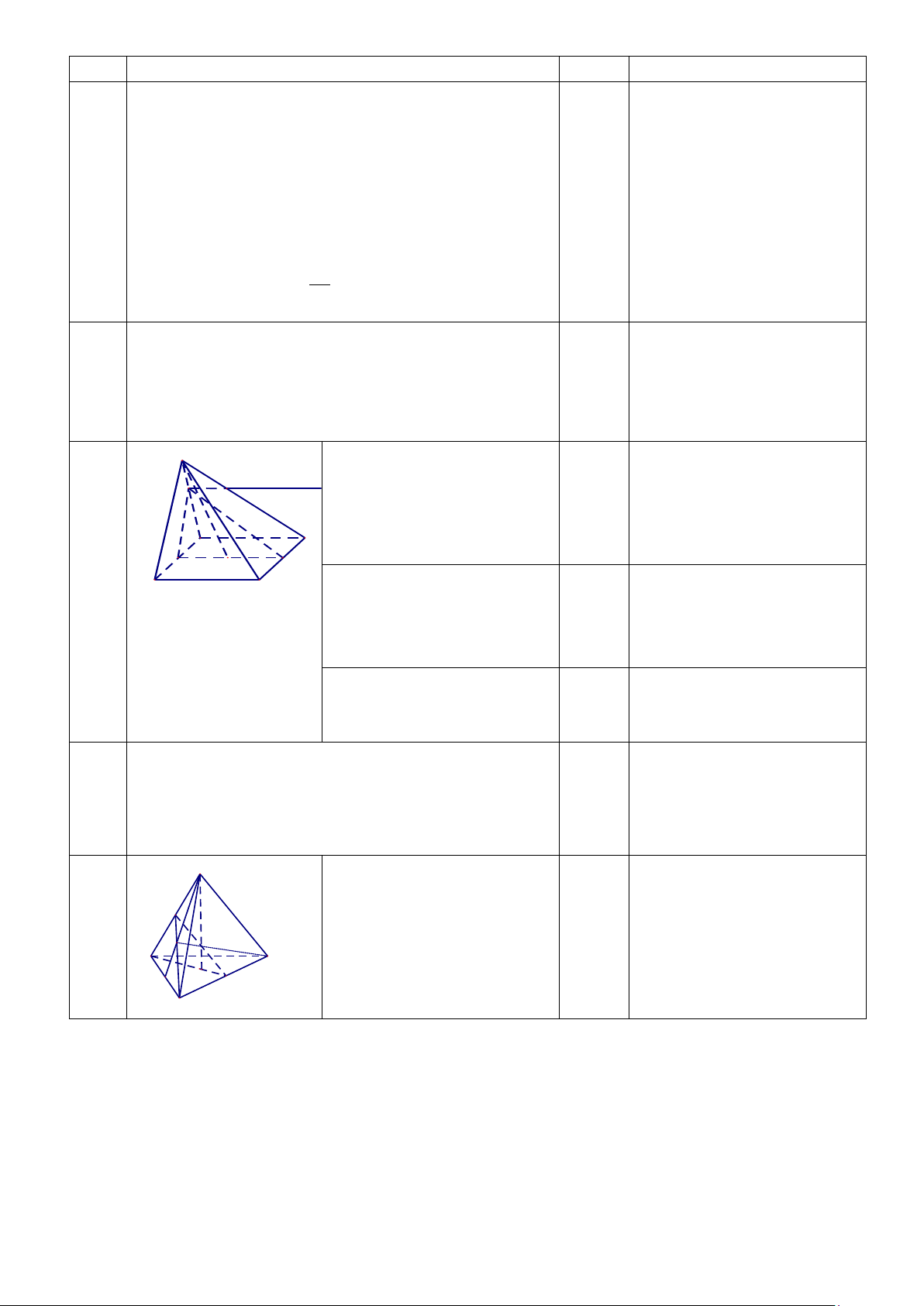
b) Cho tứ diện ABCD có M, N, P lần lượt là trung điểm AB, BC, CD. Gọi G là trọng tâm
tam giác BCD; AG cắt MP tại I, AN cắt CM tại J. Chứng minh rằng ba điểm D, I, J thẳng hàng. -HẾT-
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ I _ MÔN TOÁN 11
Năm học 2019 – 2020 Câu Hướng dẫn chấm Điểm Lưu ý 1.a Pt 0.5đ π π 3x + = + k2 1 π π 4 6 ⇔ sin(3x + ) = ⇔ (k ∈ ) 4 2 π π
3x + = π − + k2π 4 6 π − k2π x = + 0,25 36 3 ⇔ 7π k2π x = + 0,25 36 3
1.b Chia hai vế pt cho 2, pt π 1 sin(2x − ) = 0,75 6 2 0,25 π π x − = + k2π π 6 6 = + π x k2 π π 3 (k ∈ Z) x 0,25x2 − = π − + k2π = π + π x k2 6 6 1.c 2 0.75
cot x − tan x + 4sin 2x = sin 2x đ kπ Đk: sin2x ≠ 0 ⇔ x ≠ 2 cos x sin x 2 PT ⇔ − + 4sin 2x = sin x osx c sin 2x 2
⇔ 2cos2x + 4sin 2x − 2 = 0 0,25 2 ⇔ 2
− cos 2x + cos2x +1 = 0 x = kπ (l) os c 2x =1 0,25x2 π 1 ⇔
− ⇔ x = + kπ (n) (k ∈) os c 2x = 3 2 π x − = + kπ (n) 3
2.a Gọi số cần tìm có dạng ab
1đ a∈{3, 4, 5} có 3 cách, b∈X có 4 cách 0,25x4
Quy tắc nhân, vậy có 12 cách lập số. 2.b k 0,25x2 12 k 2 −k 1 − k k 24−3k 1đ T = = − + C x C x k 1 1 12 ( ) 12 ( ) ( ) x
Hệ số x12 => 24 - 3k = 12 0,25x2
k = 4. Vậy hệ số là 495 Câu Hướng dẫn chấm Điểm Lưu ý 2.c . n(Ω) 4 = C 0,25 16 1đ TH1: 1 đỏ , 3 xanh 1 3 C .C 4 5 0,25
TH2: 1 đỏ, 1 vàng, 2 xanh 1 1 2 C .C .C 4 7 5 0,25 1 2 1
TH3: 1 đỏ, 2 vàng , 1 xanh : C .C .C 4 7 5 n( A) = ⇒ P( A) 37 740 = 0,25 91 3.a 2u + 3d = 20 1,0 Lập hệ 1 2u +10d = 29 − 1 0,25x4 Tìm đúng u1 =20,5; d=-7 S = 110 − 10 4 S Hình vẽ : 0,25 2.5đ a) K I Lập luận điểm S chung Lập luận điểm O chung 0,25x3 A D M
Kết luận SO = (SAC)∩(SBD) N O b)Chọn mp phụ (SAD) B C (MNK)∩(SAD)=x’Kx//AD x’Kx∩SD = I 0,25x3
Lập luận I là điểm cần tìm a) cm: BC//(SMN) 0,25x3 cm: SB//(SMN) Kết luận (SBC)//(SMN) 5a
Tính được véc tơ AB = (2; -3) 0,25x3 x ' = x + 2 x '− 2 = x
0.75 Viết được công thức: ⇔ y ' y 3 = − y '+ 3 = y
Tìm được d’: 3x -2y -11 = 0 5b A C1 :
Cm: I ∈(CMD) ∩( ADN ) 0.75 Cm : D,I,J thuộc (CMD) đ
Cm: J ∈(CMD) ∩( ADN ) M Cm: D,I,J thuộc (AND) 0,25x3 J I KL: D,I,J thẳng hàng KL : D,I,J thẳng hàng B D N G P C
Document Outline
- Toán 11 _ (1CT) - HAN THUYEN Tuấn Nguyễn Ngọc
- Đáp án Toán 11 _ (1CT) - HAN THUYEN Tuấn Nguyễn Ngọc




