SỞ GIÁO DỤC VÀ ĐÀO TẠO TPHCM ĐỀ KIỂM TRA HỌC KỲ I
TRƯỜNG THPT LÊ TRỌNG TẤN NĂM HỌC 2019 – 2020 Môn: Toán – Khối: 11 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút
(Học sinh không phải chép đề vào giấy làm bài)
Họ và tên học sinh: ......................................................................Số báo danh: ........................... Lưu ý:
 Phần chung tất cả học sinh đều làm.
 Phần riêng học sinh chỉ làm theo phân ban học trên lớp.
A. PHẦN CHUNG ( 7.0 điểm)
Bài 1. (1.5 điểm) Giải phương trình: a) 2
4cos 5x  9cos5x  5  0 b) 2 2 2 2 3
cos x  cos 2x  cos 3x  cos 4x  2 Bài 2. (2.0 điểm)
a) Với các chữ số 0, 1, 2, 3, 4, 5 có thể lập được bao nhiêu số tự nhiên lẻ có 3 chữ số.
b) Một lớp có 10 học sinh nam và 35 học sinh nữ. Có bao nhiêu cách chọn 5 bạn học sinh
sao cho trong đó có đúng 3 học sinh nữ ?
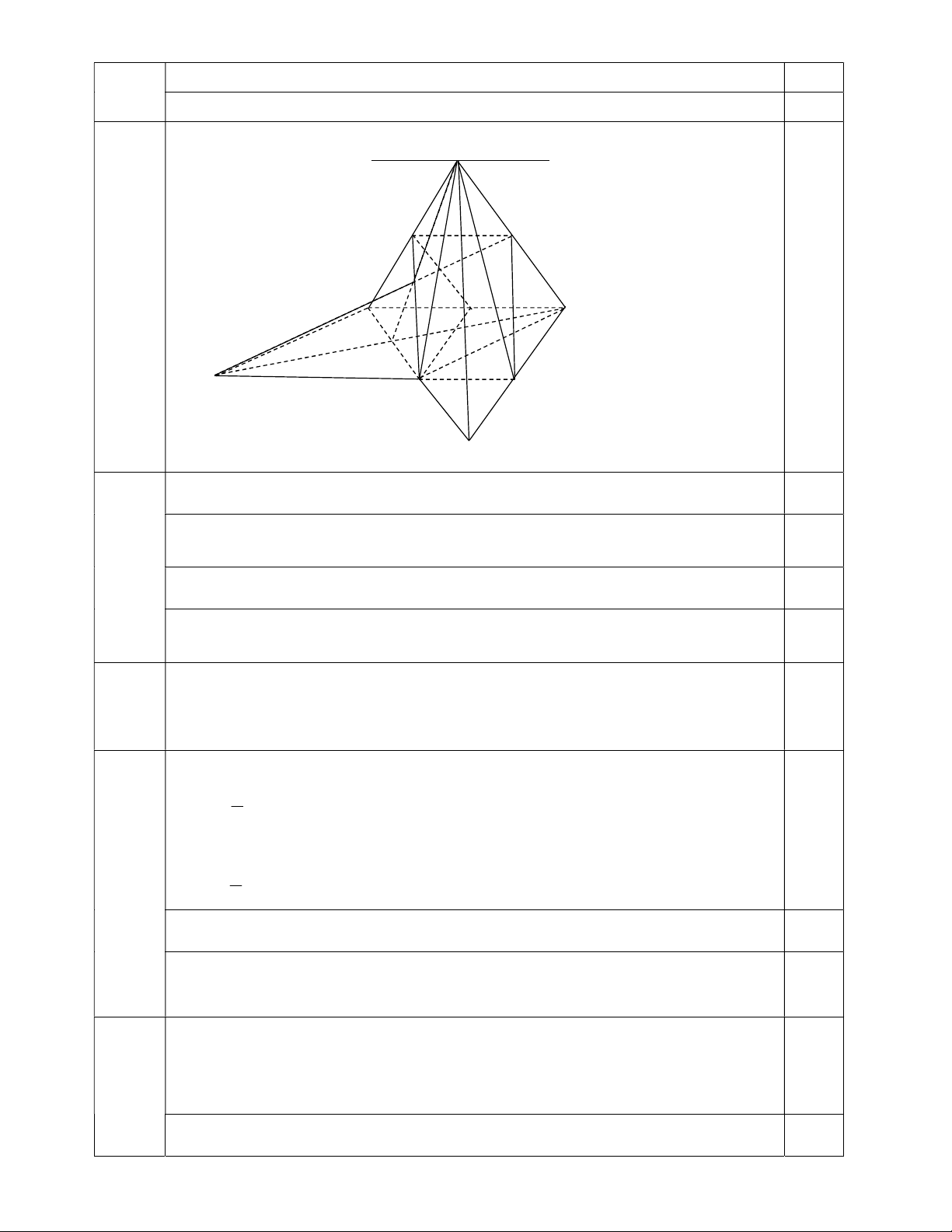
Bài 3. (3.5 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình thang, AD / /BC, AD  2BC .
Gọi M , N, I lần lượt là trung điểm của các cạnh S , A AD, S . D
a) Tìm giao tuyến của SAB và SCD ; SAD và SBC .
b) Gọi G là trọng tâm SAB . Tìm giao điểm K của GI với mặt phẳng  ABCD .
c) Chứng minh CI / / BMN  .
d) Chứng minh GI, KD, BC đồng quy.
B. PHẦN RIÊNG (3.0 điểm)
PHẦN DÀNH RIÊNG CHO BAN TỰ NHIÊN
Bài 4. (1.0 điểm) Một hộp đựng 7 viên bi trắng được đánh số từ 1 đến 7, 10 viên bi xanh được
đánh số từ 1 đến 10 và 8 viên bi đỏ được đánh số từ 1 đến 8. Chọn ngẫu nhiên 4 viên bi.
Tính xác suất của biến cố A để “ 4 viên bi được chọn có đủ 3 màu và tích các số trên 4 viên
bi đó là một số lẻ”. 13  1 
Bài 5. (1.0 điểm) Tìm số hạng chứa 3 x trong khai triển x    .  x 
Bài 6. (1.0 điểm) Tìm n , biết: 2 2 2 2 C  2C  2C  C  149. n 1  n2 n3 n4
PHẦN DÀNH RIÊNG CHO BAN XÃ HỘI
Bài 4. (1.0 điểm) Một hộp đựng 4 viên bi đỏ, 5 viên bi trắng và 6 viên bi vàng. Chọn ngẫu nhiên
4 viên bi từ hộp. Tính xác suất để 4 viên bi được chọn đủ cả 3 màu. 9  1 
Bài 5. (1.0 điểm) Tìm số hạng chứa x trong khai triển x  .    x 
Bài 6. (1.0 điểm) Tìm n , biết: n 1  n C  C  7 n  3 n4 n3  
……..….…………….HẾT……………………….
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM TỰ LUẬN TOÁN 11 – ĐỀ SỐ 1 Bài Nội dung Điểm
Đặt cos5x  t , điều kiện t  1  ,  1 0.25 1.a
(1.0 đ) Phương trình trở thành: 2 4t  9t  5  0 0.25 t  1 (n) 0.25 k2   5
 cos5x  1  5x  k2  x  (k  ) t  (l) 5  4 k2 0.25
Vậy phương trình có 1 họ nghiệm x  (k  ) 5 1.b 2 2 2 2 3
(0.5 đ) cos x  cos 2x  cos 3x  cos 4x  2
1 cos 2x 1 cos 4x 1 cos6x 1 cos8x 3 0.25      2 2 2 2 2
 cos 2x  cos4x  cos6x  cos8x 1  0 2
 cos 2x  cos4x  cos6x  2cos 4x  0 2
 2cos4xcos 2x  cos4x  2cos 4x  0
 cos 4x2cos2x 1 2cos4x  0  x  x    2 cos 4 2cos 2 1 2 2cos 2x   1  0  x 2
cos 4 2cos 2x 1 4cos 2x  2  0  x 2
cos 4 2cos 2x  4cos 2x   1  0    0.25     cos 4x  0 4x k  2    1 5     1 5 cos 2x    2x  arc cos  k2 4  4    1 5  1   5 cos 2x   2x  arc cos  k2  4  4    x   k  8 4   1 1   5  x   arccos  k k    2 4   1 1   5 x   arc cos  k  2 4 2.a
Gọi abc là số tự nhiên cần tìm 0.25
(1.0 đ) a : có 5 cách chọn b : có 6 cách chọn 0.25 c : có 3 cách chọn 0.25 Vậy có 6.5.3  90 số 0.25 2.b
Chọn 3 học sinh nữ trong 35 học sinh nữ ta có: 3 C35 0.5
(1.0đ) Chọn 2 học sinh nam trong 10 học sinh nam ta có: 2 C10 0.25 Vậy có: 3 2 C .C  294525 (cách chọn) 35 10 0.5 3 S x M I G A N D E K C B T 3.a S (SAB)  (SCD) 0.25 (1.0 đ)
Trong  ABCD có AB không song song với CD nên 0.25
T  AB  CD  T  (SAB)  (SCD)  (SAB)  (SCD)  ST 0.25
Trong  ABCD có AD không song song với BC nên 0.25
(SBC)  (SAD)  Sx / /AD / /BC 3.b Gọi E là trung điểm AB 0.25x
(1.0đ) Trong SDE gọi K  GI  DE 4  K  GI   ABCD 3.c BC / / AD 0.5 (1.0đ)  1 BC  AD  BC / / 2 MI   
 BCIM là hình bình hành. MI / / AD  BC  MI  1 MI  AD  2 CI / /BM 0.25 C  I   BMN  0.25 Mà   CI / / BMN  BM   BMN  3.d G
 I  BCIM  SKD 0.25 (0.5đ) 
Ta có KD  SKD   ABCD BC  BCIM   ABCD
Mà GI  KD  K nên ta có GI, KD, BC đồng quy tại K 0.25
PHẦN DÀNH RIÊNG CHO BAN TỰ NHIÊN 4 n  4  C 0.25 25 (1.0đ) n  A  2 2 2
C .4.5  C .4.5  C .4.4  400 0.5 4 4 5 0.25  P  A n A 8   n 253 5
Gọi số hạng tổng quát là 0.5 (1.0 đ) k   T  C       x13k 1 . C  
x13k . 1k xk C   1 k x132k k k k k 1 13 13 13  x 
Theo giả thiết  x132k 3
 x  13 2k  3  k  5 0.25 Vậy số hạng chứa 3 x là: C  5 1  x3 5 3  1287x 0.25 13 6 n  1 0.25 (1.0 đ) Điều kiện:  . n   Ta có: 2 2 2 2 C 0.25 1  2C 2  2C 3  C    4  149 n n n n (n 1)! (n  2)! (n  3)! (n  4)!   2  2   149 2!(n 1)! 2!n! 2!(n 1)! 2!(n  2)!   0.25 2 n 5 (n)
 n  4n – 45  0   n  9  (l) Vậy: n  5. 0.25
PHẦN DÀNH RIÊNG CHO BAN XÃ HỘI 4 n 4  C  1365 0.25 15 (1.0 đ) n  2 2 2
A  C .5.6  C .4.6  C .4.5  720 0.5 4 5 6 n A 48 0.25 Xác suất: P  A     . n 91 5
Gọi số hạng tổng quát là 0.5 (1.0 đ) k   T  C    x9k 1 . C  
x9k . 1k xk C   1 k  x92k k k k k 1 9 9 9  x 
Theo giả thiết  92k x
 x  9  2k 1  k  4 0.25 Vậy số hạng chứa 3 x là: C  4 4 1 x  126x 0.25 9 6 n  1 0.25 (1.0 đ) Điều kiện:  n   Ta có: n 1  n C  C  7(n  3)   n   n 1 n n n 4 3
Cn3  Cn3  Cn3  7(n  3) 0.25 (n  2)(n  3) 0.25   7n  3 2!
 n  2  7.2! n  12 0.25
Chú ý: Học sinh có thể làm Toán bằng cách khác và vẫn được tính điểm nếu đúng