


Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ KIỂM TRA HỌC KÌ I – NĂM HỌC 2019 – 2020 TP. HỒ CHÍ MINH Môn: TOÁN Khối 11
TRƯỜNG THPT NGUYỄN HỮU THỌ Thời gian làm bài: 90 phút (không kể thời gian phát đề) ĐỀ CHÍNH THỨC
Bài 1 (2 điểm): Giải các phương trình sau: 1 a) sin 2x
. Phương trình đã cho có bao nhiêu nghiệm trong khoảng (-3 ; 1) ? 3 2 b) cos 2x 3sinx + 4 = 0 Bài 2 (1,5 điểm): 8
a) Tìm hệ số của số hạng chứa x8 trong khai triển của nhị thức: 2 x 2
b) Cho số nguyên dương n thỏa 2 A 2 C 2 2 n 80 . n n 2 n
Tìm số hạng không chứa x trong khai triển của nhị thức: x , x 0 4 x
Bài 3 (1,5 điểm): Một túi chứa 14 quả cầu khác nhau gồm 7 quả cầu màu đỏ, 4 quả cầu màu xanh
và 3 quả cầu màu vàng. Chọn ngẫu nhiên đồng thời 3 quả cầu. Tính xác suất để:
a) 3 quả cầu được chọn đều là màu đỏ.
b) 3 quả cầu được chọn có nhiều hơn 1 màu.
Bài 4 (1 điểm): Tìm số hạng đầu và công sai của cấp số cộng u biết u u 36 7 3 n S 22 4
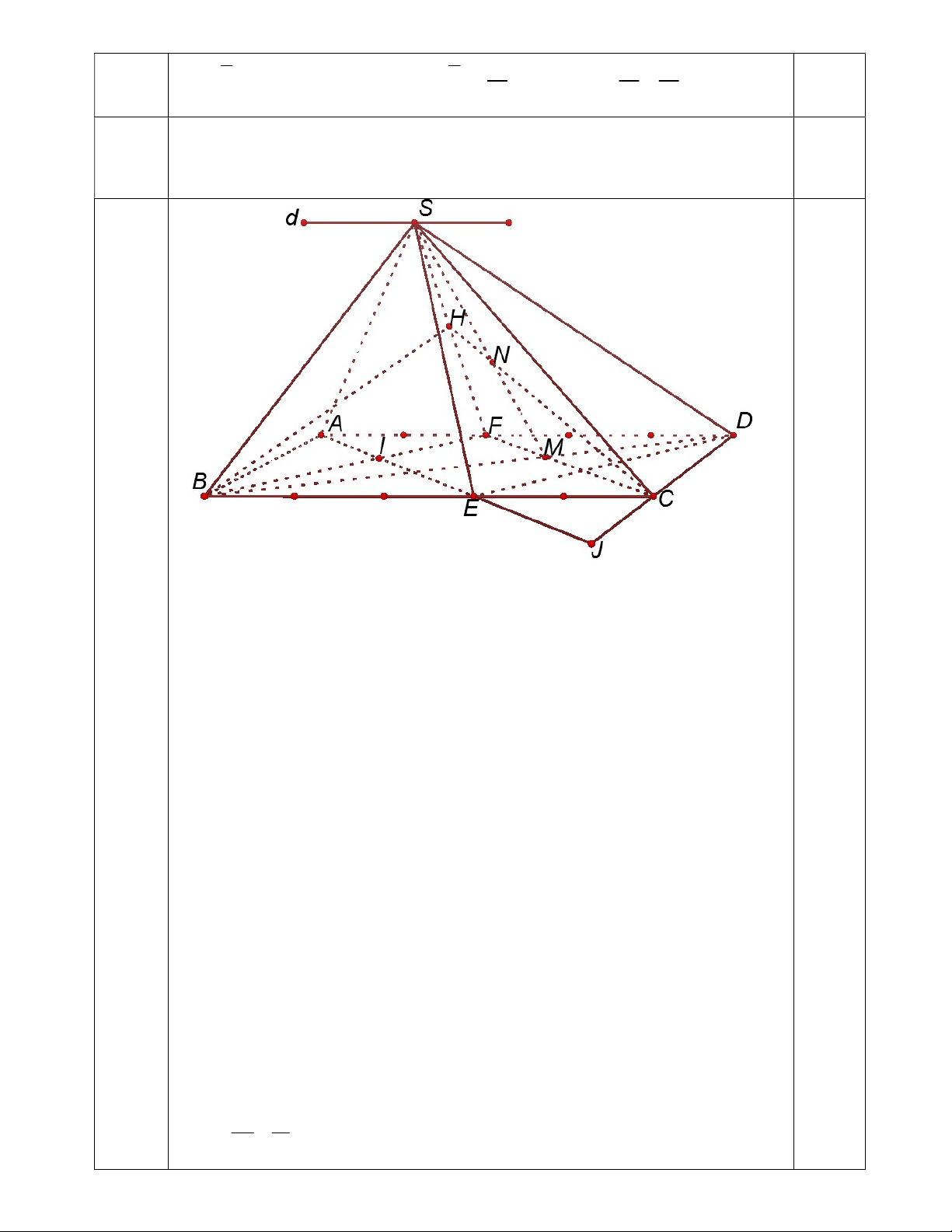
Bài 5 (3 điểm): Cho hình chóp S.ABCD có ABCD là hình bình hành. Gọi E,F lần lượt thuộc cạnh BC,AD sao cho 3 BE BC , 2
AF AD ;H là trung điểm SF; J là giao điểm của AE và CD. 5 5
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
b) Tìm giao điểm của đường thẳng CH và mặt phẳng (SBD).
c) Chứng minh đường thẳng FC song song với mặt phẳng (SAE). JE 10
d) Một mặt phẳng chứa BH và song song ED cắt AE tại I. Chứng minh . JI 19
Bài 6 (1 điểm): Cho sơ đồ mạch điện có 9 công tắc, mỗi công tắc có 2 trạng thái đóng và mở.
Hỏi có bao nhiêu cách đóng – mở 9 công tắc trên để mạng điện thông mạch từ A đến Z? (Hết)
TRƯỜNG THPT NGUYỄN HỮU THỌ
ĐÁP ÁN TOÁN 11 –HKI – 2019-2020 CÂU ĐÁP ÁN ĐIỂM 1a 2x k 2 x 1 k 2x 3 6 4 sin (k Z) . 0.25x3 3 2 5 7 2x k 2 x k 3 6 12 0.25
Phương trình đã cho có 3 nghiệm trong khoảng (-3 ; 1) 1b sinx 1(n) 2
cos2x 3sinx + 4 = 0 (1 2sin x) 3sin x 4 0 5 sinx (l) 0.25x3 2 x k 2 (k Z) 2 0.25 k 2 8k k k 16 2 k k 2.a T C (x ) .2 C x .2 k 1 8 8 0.25
16 2k 8 k 4 0.25 Hệ số cần tìm 4 4 C 2 1120 8 0.25 2 2 2 2b A 2C n 80 ,n 2 n n n! n! 2 2. n 80 (n 2)! 2!(n 2)! 0.25 n 10 (n) 2 2
n(n 1) n(n 1) n 80 n 2n 80 0 n 8 (l) k 2 k k 10 k k 105 T C x . C (2) . k x k 1 10 4 10 x 0.25
10 5k 0 k 2 2 2 T C 2 360 3 10 0.25 3.a n 0.25 Ω 3 C 364 14
Gọi biến cố A: “3 quả cầu được chọn đều là màu đỏ” n A 0.25 nA 3 5 C 35 PA 7 nΩ 52 0.25 3b
Gọi biến cố B: “3 quả cầu được chọn có nhiều hơn 1 màu” 0.25
B : “3 quả cầu được chọn có đúng 1 màu” 10 10 81 0.25x2 nB 3 3 3
C C C 40 PB PB 1 7 4 3 91 91 91 4 u u 36 2u 8d 36 u 2 7 3 1 1 0.25 S 22 4u 6d 22 d 5 x4 4 1 5
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
Ta có S SAD SBC 0.25 0.25 Mặc khác SAD A ,
D SBC BC, AD / /BC (gt)
Suy ra: d SAD SBC, d qua S, d / / A , D d / /BC 0.25
b) Tìm giao điểm của đường thẳng CH và mặt phẳng (SBD).
Trong (ABCD) gọi M CF BD . Suy ra SM SCF SBD 0.25 N CH Trong (SCF) gọi N CH SM . N SM SM SBD N CH SBD , 0.25x2
c) Chứng minh đường thẳng FC song song với mặt phẳng (SAE).
FC SAE, AE SAE 0.25 FC / / AE do AECF hbh 0.25 Suy ra, FC//(SAE) 0.25
d) Một mặt phẳng chứa BH và song song ED cắt AE tại I. Chứng minh JE 10 . JI 19
Tìm đúng 2 giao điểm I, J JE JE JE JE JE 25 2 10 0.25 . JI JA AI 2 2 3 19 19 5 19 JA EA JA . JA JA 0.25x2 5 5 5 25 6
Thông mạch qua MN có 26 trạng thái đóng – mở ở IJ. 0.25
Thông mạch qua IJ có 23 trạng thái đóng – mở ở MN. 0.25
trong đó chỉ có 1 trường hợp mắc song song thông mạch cả MN và IJ Vậy, có tất cả 3 6 0.25
2 2 1 71 trạng thái thông mạch điện từ A – Z. 0.25
(Học sinh có thể giải cách khác, Giám khảo dựa vào thang điểm để chấm)




