Đề thi học kì 1 Toán 11 năm 2019 – 2020 trường THPT Phạm Phú Thứ – TP HCM

SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ KIỂM TRA HỌC KỲ I THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2019 – 2020
TRƯỜNG THPT PHẠM PHÚ THỨ Môn: Toán – Khối: 11
Thời gian làm bài: 90 phút (không kể thời gian phát đề) ĐỀ CHÍNH THỨC
(Thí sinh không phải chép đề vào giấy làm bài) ĐỀ 1
Câu 1. (1 điểm) Giải phương trình sau:       cos  2x  3 sin  2x  2.      3   3 
Câu 2. (1 điểm) Cho tập hợp A = {0; 1; 2; 3; 6; 7; 8}, từ các phần tử của A có thể lập được
bao nhiêu số tự nhiên có 5 chữ số khác nhau và là số chẵn.
Câu 3. (1 điểm) Giải phương trình: 2 2 C  3A  P  20  0. n n 1  3 8
Câu 4. (1 điểm) Tìm số hạng chứa x4 trong khai triển của biểu thức  1 3  2x    với x  0 .  x 
Câu 5. (1 điểm) Một hộp chứa 10 bóng đỏ và 7 bóng xanh. Từ hộp lấy ngẫu nhiên ra 5 quả
bóng, tính xác suất để lấy được ít nhất 3 quả bóng xanh.
Câu 6. (1 điểm) Tìm số hạng đầu 1
u và công sai d của cấp số cộng un  biết: 4u2  u3  5  . u  4  6 S  1  5
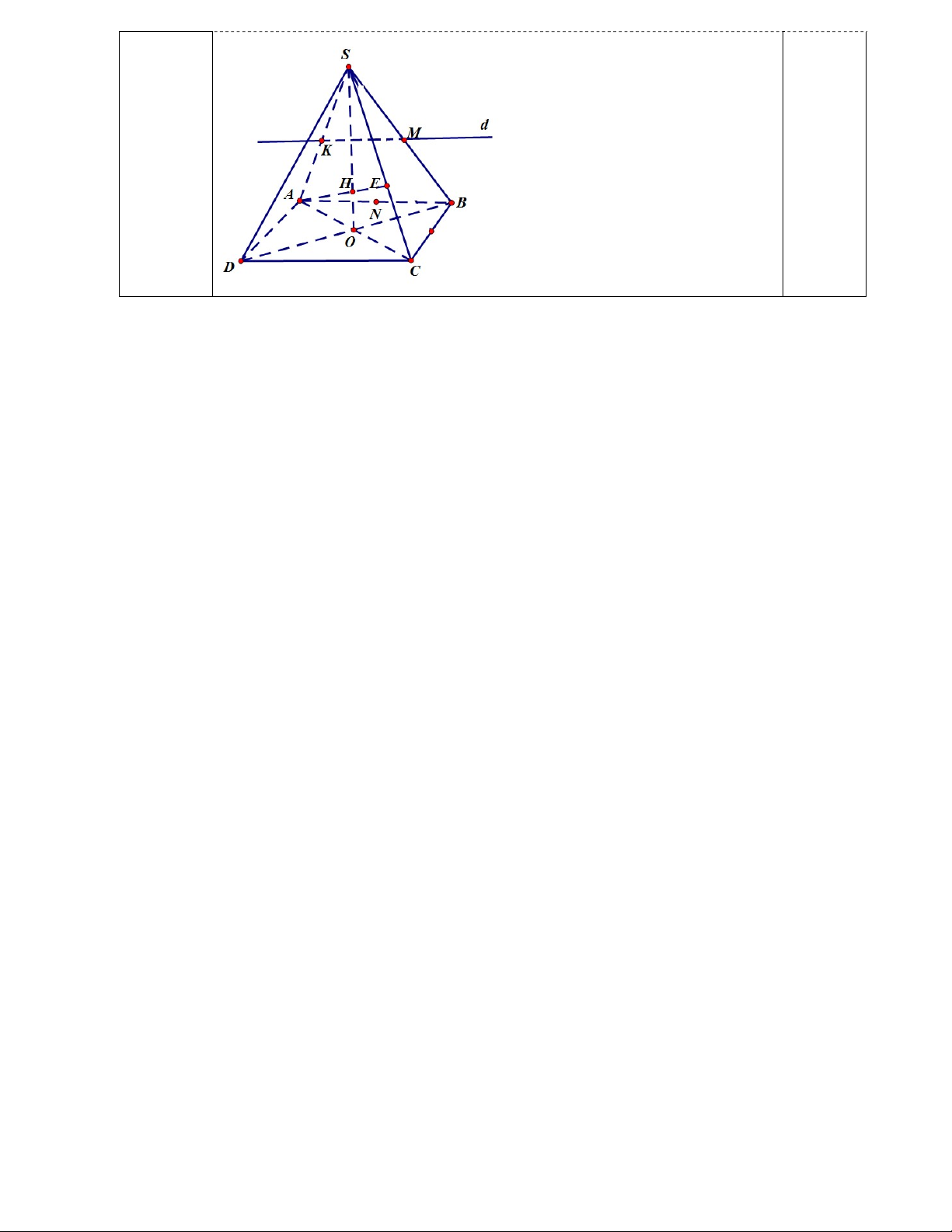
Câu 7. (4 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M, N lần
lượt là trung điểm của SB, AB.
a)(0.75 điểm) Tìm giao tuyến của (SAC) và (SBD).
b)(0.75 điểm) Tìm giao tuyến của (MCD) và (SAB).
c)(0.5 điểm) Chứng minh: BC // (SON) .
d)(1 điểm) Gọi E thuộc cạnh SC sao cho SE = 2EC. Tìm giao điểm của đường thẳng AE và (SBD).
e)(1 điểm) Tìm thiết diện của hình chóp khi cắt bởi (MCD). Thiết diện đó là hình gì?Giải thích. -------Hết-------
Thí sinh không sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm ĐÁP ÁN Bài 1       0,25đ cos  2x  3 sin  2x  2      3   3  1    3    2  cos  2x  sin  2x      2  3  2  3  2         2  sin .cos  2x  cos .sin  2x      6  3  6  3  2     2 0,25đ  sin   2x     6 3  2      2x   k2       sin   2x  sin 6 4     ( k   )  6  4   0,25đ
  2x     k2   6 4  5 x   k 0,25đ  24   . 11 x   k  24
Gọi số cần tìm là abcde Bài 2 0.25 Trường hợp 1: e  0 e có 3 cách a có 5 cách b có 5 cách c có 4 cách d có 3 cách có 3.5.5.4.3  900 Trường hợp 2: e  0 0.25 e có 1 cách a có 6 cách b có 5 cách 0.25 c có 4 cách d có 3 cách có 1.6.5.4.3  360 Vậy có 1260 số 0.25 2 2 C  3A  P  20  0 n n 1  3 Bài 3 n   0.25 Điều kiện : n  3 n! n   1 ! 0.25     n   3 n  26 0 2 !2! 3 ! nn   1 n  2! 3n   1 n  2n  3!      n   n   26 0 2 !2 3 ! 2  5  n 17n  40  0 0.25 n  5(N)   8  0.25 n  (loai)  5 Ta có: Bài 4     C  k k k 2x 8 1 3 0.25 8    x  8  C 2   k k k 244 1 k x 0.25 8
Theo đề bài ta có: 24  4k  4  k  5 0.25 Số hạng chứa 4 x là C 2  5 5 3 4 1 x 8 0.25 Bài 5 Không gian mẫu:
Lấy ra 5 quả bóng trong 17 quả: 5 C cách 17 5  n( )   C  6188. 17 0.25
Gọi A là biến cố “Lấy được ít nhất 3 quả bóng xanh” . TH1: Lấy 3 quả bóng xanh: 3 C cách 7 0.25 Lấy 2 quả bóng đỏ: 2 C cách 10 TH2: Lấy 4 quả bóng xanh: 4 C cách 7 Lấy 1 quả bóng đỏ: 1 C cách 10 TH3: Lấy 5 quả bóng xanh: 5 C cách 7 3 2 4 1 5  0.25 n( )
A  C .C  C .C  C  1946 7 10 7 10 7 n( ) A 1946 139 Vậy P( ) A    0.25 n() 6188 442 Bài 6 4u  u  5 2 3  u  4  6 S  1  5
4u  d  u  2d  5 1   1   0.5   62u  5d 1  u   3d   15 1  2 0.25 3  u  2d  5 1   7u 18d  15  0.25 1 u   3 1   d   2  a) Bài 7 S (SAC)  (SBD) (1). 0,25đ
Trong (ABCD) : AC  BD  O . O
  AC, AC  (SAC)  O  (SAC)  O
  BD, BD  (SBD)  O  (SBD)  O(SAC)  (SBD) (2). 0,25đ
(1), (2)  SO  (SAC)  (SBD). 0,25đ b) M  (MCD)   M (MCD)  (SAB) 0,25đ
M  SB, SB  (SAB)  M (SAB) Ta có AB / /CD  0,25đ AB  (SAB) CD  (MCD) 
 d  (MCD)  (SAB) . d qua M và song song AB, CD. c) Ta có 0.25 BC  SON  O  N / /BC
( do ON là đường trung bình tam giác ABC) 0.25 O  N  (SON) BC//(SON)
d) Trong (SAC) : AE  SO  H . 0,25đ H  AE  0.5
H  SO, SO  (SBD)  H  (SBD) H  E A  S D B  0,25đ e) Gọi K  d  SA M D C  SAB  MK 0.25 MCDS D A   KD 0.25 MCDSBC  MC MCDS D C   CD
Vậy thiết diện tạo bởi  0.25 MCD và hính chóp là M D K C 0.25 M D
K C là hình thang vì MK / / D C
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ KIỂM TRA HỌC KỲ I THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2019 – 2020
TRƯỜNG THPT PHẠM PHÚ THỨ Môn: Toán – Khối: 11
Thời gian làm bài: 90 phút (không kể thời gian phát đề) ĐỀ CHÍNH THỨC
(Thí sinh không phải chép đề vào giấy làm bài) ĐỀ 2
Câu 1. (1 điểm) Giải phương trình sau:       sin  3x  3 cos  3x  1.      3   3 
Câu 2. (1 điểm) Cho tập hợp S  {0;2;3;5;7;8;9}.Từ các phần tử của S có thể lập được bao
nhiêu số tự nhiên có 5 chữ số khác nhau và chia hết cho 5.
Câu 3. (1 điểm) Giải phương trình: 2 2 C  4 A  P 100  0. 2n n 1  2 8  3 
Câu 4. (1 điểm)Tìm số hạng chứa x7 trong khai triển của biểu thức 2 x    với x  0 .  x 
Câu 5. (1 điểm) Một hộp chứa 10 viên bi đen và 20 viên bi trắng. Từ hộp lấy ngẫu nhiên 5 viên
bi, tính xác suất để lấy được ít nhất 3 viên bi đen.
Câu 6. (1 điểm) Tìm số hạng đầu 1
u và công sai d của cấp số cộng un  biết 2u3  u4  1   . u  2  4 S  11
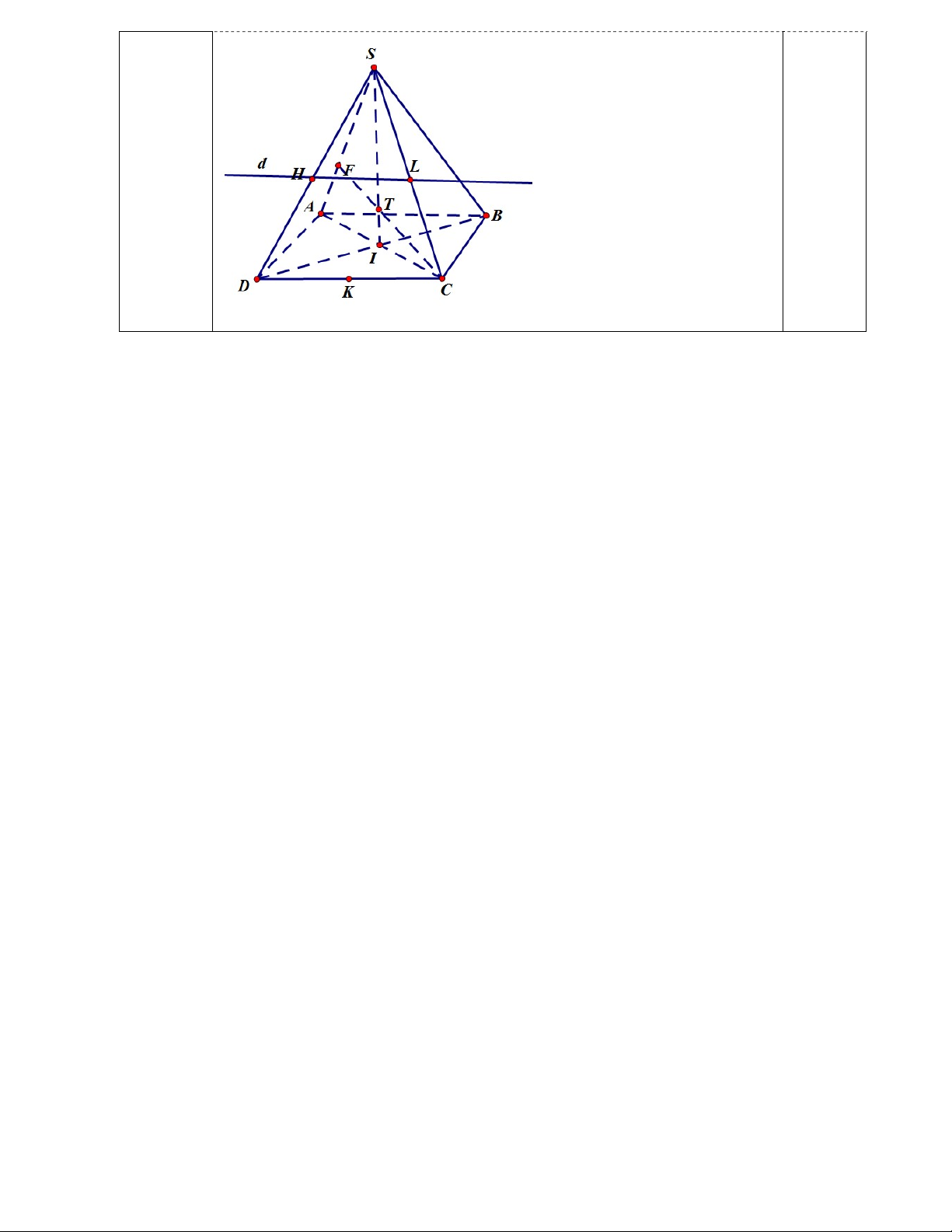
Câu 7. (4 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm I. Gọi H, K lần
lượt là trung điểm của SD, CD.
a)(0.75 điểm) Tìm giao tuyến của (SAC) và (SBD).
b)(0.75 điểm) Tìm giao tuyến của (HAB) và (SCD).
c)(0.5 điểm) Chứng minh: AD // (SIK).
d)(1 điểm) Gọi F thuộc cạnh SA sao cho SF = 2FA. Tìm giao điểm của đường thẳng CF và (SBD).
e)(1 điểm) Tìm thiết diện của hình chóp khi cắt bởi (HAB). Thiết diện đó là hình gì?Giải thích. -------Hết-------
Thí sinh không sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm ĐÁP ÁN Bài 1       0,25đ sin  3x  3 cos  3x  1      3   3  1    3    1  sin  3x  cos  3x      2  3  2  3  2         1  cos .sin  3x  sin .cos  3x      3  3  3  3  2 1 0,25đ  sin3x  2       3x k2   sin 3x  sin 6   ( k   ) 6  0,25đ 3x     k2   6   k2 x   0,25đ  18 3   k  . 5 k2 x    18 3
Gọi abcde là số tự nhiên cần lập. Bài 2 TH1: Chọn e  0 : 1 cách Chọn a  0 : 6 cách 0.25 Chọn , b , c d : 3 A cách 5  Có 3 1.6.A  360 số. 5 TH2: Chọn e  5 : 1 cách 0.25 Chọn a  0,e: 5 cách 0.25 Chọn , b , c d : 3 A cách 5  Có 3 1.5.A  300 số 5
Vậy có 360  300  660 số 0.25 2 2 C  4 A  P 100  0. 2n n 1  2 Bài 3 n   0.25 Điều kiện : n  1 2n! n   1 ! 0.25     n   4 n  102 0 2 2 !2! 1 ! 2n2n  
1 2n  2! 4n   1 nn   1 !      n   n   102 0 2 2 !2 1 ! 2  2  n  5n 102  0 0.25 n  6(N)   1  7 0.25 n  (loai)  2 Số hạng tổng quát: Bài 4 C x  k k 8k k  3  k  k 3 2 16 2 k k 163  C .x .  C .3 . k x 0.25 8   8 k 8  x  x 0.25
Cho: 16  3k  7  k  3
Vậy số hạng cần tìm là: 3 3 7 7 C .3 .x  1512 x . 0.25 8 0.25 Bài 5 n  5  C 142506 0.25 30
Gọi A là biến cố “chọn được ít nhất 3 viên bi đen”. TH1: 3 đen, 2 trắng 0.25 3 2 C .C  22800 10 20 TH2: 4 đen, 1 trắng 4 1 C .C  4200 10 20 TH3: 5 đen 5 C  252 10
n A  22800  4200  252  27252 0.25   nA 27252 1514 P A    n  142506 7917 0.25 Bài 6 2u 3  u4  1  u  2  S4  1  1
2u  2d  u  3d  1 1   1   0.25   42u  3d 0.25 1  u   d   1  1 1  2 u   d  1  1   0.25 5u  7d  1  1  1 u   2 1   d   3  0.25 a) Bài 7 S (SAC)  (SBD) (1). 0,25đ
Trong (ABCD) : AC  BD  I .
I  AC, AC  (SAC)  I  (SAC)  0,25đ
I  BD, BD  (SBD)  I  (SBD)  I (SAC)  (SBD) (2).
(1), (2)  SI  (SAC)  (SBD). 0,25đ b) H  (HAB)   H (HAB)  (S D C ) (1). 0,25đ
H  SD, SD  (SCD)  H  (SCD) Ta có AB / /CD  0,25đ AB  (HAB) (2) CD  (SCD) 
(1), (2)  d  (HAB)  (SCD). 0.25
Trong đó d đi qua H và song song AB, CD c) Ta có 0.25 AD  SIK   A D / / IK
( do IK là đường trung bình tam giác ACD)  0.25 IK  (SIK)  D A / /(SIK)
d) Trong (SAC) : CF  SI  T . 0,25đ T  CF  0.5 T
  SI, SI  (SBD)  T (SBD) T  CF  S D B  0,25đ e) Gọi L  d  SC HABS D C   HL 0.25 HABS D A   HA 0.25 HABSBC  BL HABSAB  AB
Vậy thiết diện tạo bởi  0.25
HAB và hính chóp là HLBA 0.25
HLBAlà hình thang vì HL/ / AB
MA TRẬN ĐỀ THI HỌC KÌ 1 LỚP 11 Vận dụng Tổng: Nhận biết Thông hiểu Vận dụng cao
Câu 1. Giải phương trình lượng 1đ 1đ giác
Câu 2. Lập số tự nhiên thỏa mãn 1đ 1đ điều kiện bài toán
Câu 3. Giải phương trình chứa
công thức tổ hợp, chỉnh hợp, 1đ 1đ hoán vị
Câu 4. Tìm số hạng chứa xk 1đ 1đ trong khai triển
Câu 5. Bài toán tính xác suất 1đ 1đ
Câu 6.Tìm số hạng đầu 1 u và
công sai d của cấp số cộng un  1đ 1đ
Câu 7. Hình học không gian
a) Giao tuyến hai mặt phẳng 0.75đ
b) Giao tuyến hai mặt phẳng 0.75đ
c) Chứng minh đường thẳng 0.5đ song song với mặt phẳng 4đ
d) Giao điểm của đường thẳng 1đ và mặt phẳng
e) Tìm thiết diện của mặt phẳng 1đ và hình chóp Tổng: 3đ 2đ 4đ 1đ 10đ