TRƯỜNG THPT PHÚ HÒA
ĐỀ THI HỌC KÌ 1 NĂM HỌC 2019 - 2020 TỔ TOÁN MÔN THI: TOÁN – LỚP: 11 ĐỀ CHÍNH THỨC
Ngày thi: 19/12/2019 – Thời gian: 90 phút
Câu 1 (2,5 điểm). Giải phương trình:  a) tan x  3  0 b) sin x  sin c) 2 sin x  2cos x  2  0 8    d) sin x  3 cos x  2 e) 2 sin 3x   sin 3x(1 cot x)    4  Câu 2 (1,5 điểm). a) Tính tổng 0 1 2 2 24 24 25 25
M  C  2C  2 C ...  2 C  2 C . 25 25 25 25 25 b) Tìm hệ số của 12
x trong khai triển biểu thức x  x8 5 3 .
c) Tìm số nguyên dương n thỏa mãn 3 2 A  24C . n n Câu 3 (1,5 điểm).
a) Gieo ngẫu nhiên một con súc sắc cân đối và đồng chất hai lần. Tính xác suất để số chấm ở
lần gieo thứ nhất gấp ba lần số chấm ở lần gieo thứ hai.
b) Một hộp chứa 9 viên bi màu xanh và 8 viên bi màu đỏ. Lấy ngẫu nhiên đồng thời 6 viên bi
từ hộp đã cho. Tính xác suất để số bi xanh bằng số bi đỏ.
c) Gọi S là tập hợp các số tự nhiên gồm hai chữ số khác nhau. Lấy ngẫu nhiên đồng thời hai
phần tử của tập S . Tính xác suất để tổng hai số được chọn không chia hết cho 2. Câu 4 (1,5 điểm). u   5
a) Cho dãy số (u ) thỏa mãn 1
( n  ,n 1). Tìm u và u . n u  4u 13  2 3 n 1  n
b) Cho cấp số cộng (u ) có u  6  và d  2 . Tính S . n 1 18
c) Tìm số hạng thứ 506 của cấp số cộng 1  , 3, 7,11,....
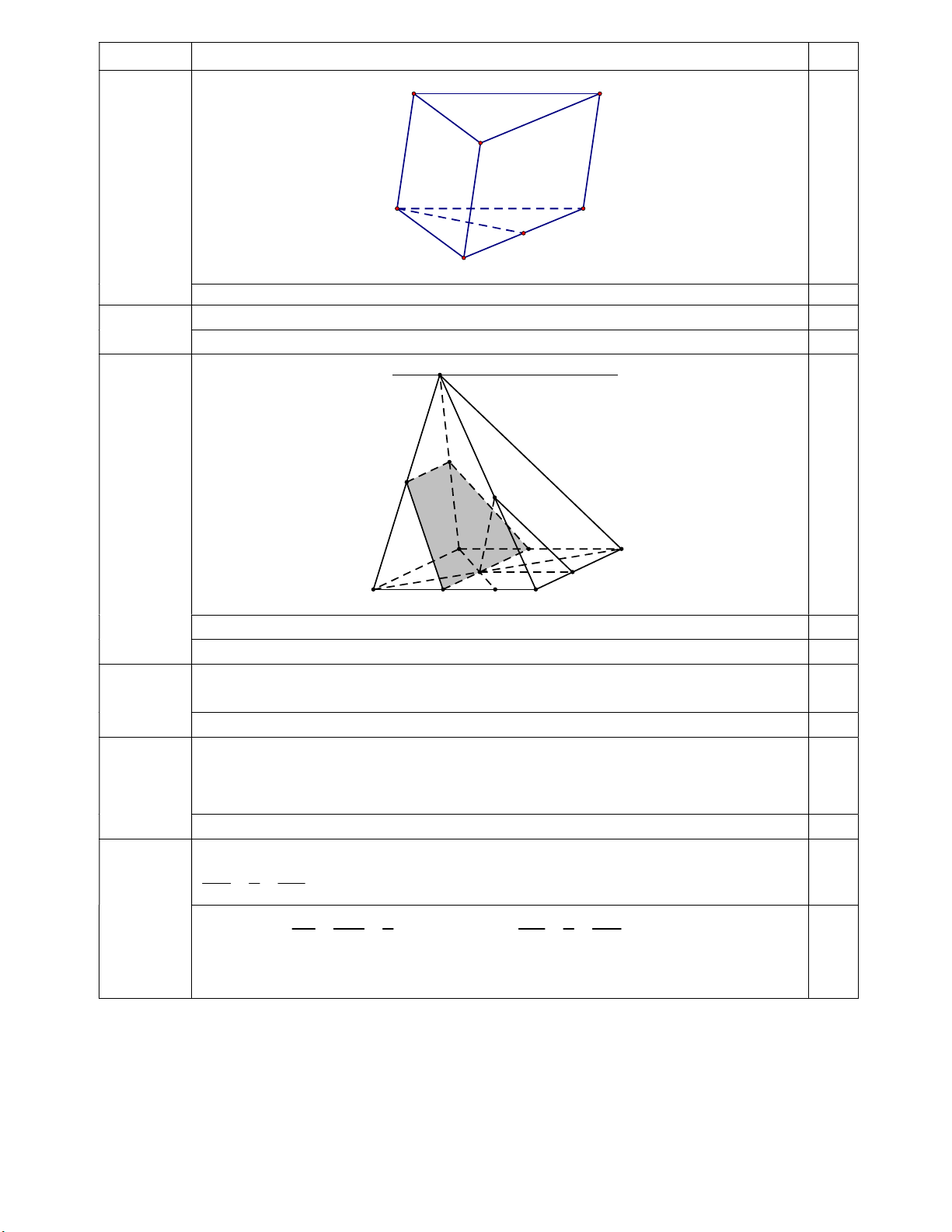
Câu 5 (1,0 điểm). Cho hình lăng trụ tam giác ABC.A' B 'C ' . a) Tứ giác ABB A   là hình gì?
b) Gọi M là trung điểm của cạnh BC . Chứng minh AM  (A'B C  ) .
Câu 6 (2,0 điểm). Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi E, F lần lượt là trung điểm của S ,
A SB . Gọi M là điểm trên cạnh BC sao cho BC  4CM , I là giao điểm của
hai đường thẳng AM và BD .
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC) . b) Chứng minh EF  DC .
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (EFI ) .
d) Gọi H là điểm trên cạnh SC sao cho 4HC  3SH . Chứng minh IH  (SAD) . Hết 1a) PT  tan x  3 0,25   x   k 0,25 3 1b)   x   k2  0,25 PT 8   7   x   k2  0,25  8 1c) PT 2
 cos x  2cos x 1  0 0,25
 cos x 1  x  k2 0,25 1d)    PT  sin x  1   0,25  3    x   k2 0,25 6 1e) ĐK: x  k k
PT  sin(3x  x)  0  x  0,25 2 
So ĐK  Nghiệm của PT: x   k 0,25 2 2a) 0 1 24 1 2 23 2 24 24 25 25
M  C  C .1 .(2)  C .1 .(2)  ... C .1.( 2  )  C .( 2  ) 0,25 25 25 25 25 25 25 25 M  (1 2)  ( 1  )  1  0,25 2b)
Số hạng tổng quát là k nk k k 8k k 404 C .a .b  C .(1) .3 . k x n 8 0,25 Vì 12
x nên 40  4k  12  k  7 Hệ số của 12 x là 7 87 7 C ( 1  ) .3  17496 0,25 8 2c) ĐK: n  3 và n  24n(n 1) PT  n(n 1)(n  2)  0,25 2  n  14 (nhận) 0,25 3a)
n()  36 . Gọi A : “Số chấm ở lần gieo thứ nhất gấp ba lần số chấm ở lần gieo thứ hai”. 0,25 A  (3;1),(6;2  )  n( ) A  2 n( ) A 1 0,25
Xác suất của biến cố A là P( ) A   n() 18 3b) 6
n()  C  12376 . Gọi A : “Số bi xanh bằng số bi đỏ” 0,25 17
Chọn 3 bi xanh trong 9 bi xanh và 3 bi đỏ trong 8 bi đỏ 3 3  n( ) A  C C  4704 9 8 n( ) A 84 0,25
Xác suất của biến cố A là P( ) A   n() 221 3c)
Số phần tử của tập S là 9.9  81. Số phần tử của không gian mẫu là 2 C  3240. 0,25 81
Tập S gồm 5.8  40 số lẻ và 1.9  4.8  41 số chẵn.
Số phần tử của biến cố “Tổng hai số được chọn không chia hết cho 2” là 40.41  1640. 1640 41 0,25 Xác suất cần tìm là  . 3240 81 4a)
u  4u 13  4.5 13  7 0,25 2 1
u  4u 13  4.7 13  15 0,25 3 2 4b) 18 S  2.(6)  (18 1).2 0,25 18   2 S 198 0,25 18 4c)
Cấp số cộng đã cho có u  1  , d  4 . 0,25 1 u  u  505d  1   505.4  2019 . 0,25 506 1 5a) A' C' B' 0,25 A C M B Tứ giác ABB A
  là hình bình hành. 0,25 5b) Ta có: (ABC)  (AB C  ) 0,25
Mà AM  (ABC) nên AM  (AB C  ) 0,25 6a) S d E F H A Q D I K B P M C
S (SAD)  (SBC) và AD  BC (vì ABCD là hình bình hành) 0,25
 (SAD) (SBC)  d, S  d,d  Ad,d  BC . 0,25 6b)
EF  AB (vì EF là đường trung bình của tam giác SAB ) 0,25
Mà AB  DC (vì ABCD là hình bình hành) Nên EF  DC 0,25 6c) EF  AB (cmt)  I (EFI )  (ABCD) 0,25
 (EFI)  (ABCD)  PQ, I  PQ, PQ  EF, PQ  AB (P BC,Q AD)
Thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (EFI) là tứ giác PQEF . 0,25 6d)
Gọi K là điểm trên cạnh CD sao cho 4KC  3KD . CH 3 CK    HK  SD  HK  (SAD) (1) 0,25 CS 7 CD DI DA 4 DI 4 DK MB  AD     3DI  4BI    BI BM 3 DB 7 DC
 IK  BC  IK  AD  IK  (SAD) (2) 0,25
Từ (1) và (2)  (IHK)  (SAD)  IH  (SAD)