

Preview text:
TRƯỜNG THPT TÂY THẠNH
ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2019 – 2020 MÔN TOÁN – KHỐI 11
Thời gian làm bài: 90 phút
(Không kể thời gian phát đề)
Họ và tên học sinh: ………………………………………………………Lớp:……….Mã số: …………
Câu 1 (2.5 điểm) Giải các phương trình sau: a. 3 tan 2x 3 0 . 7 b.
3 sin x 2sin 2x cos x 0 . c. x x2 sin cos
cos x1 2cos x 51sin x . Câu 2 (1.5 điểm)
a. Tìm số nguyên dương n thỏa mãn 2 2 C A 57P . n 2n 3 10 2 b. Tìm hệ số của 7 x trong khai triển của x . 2 x Câu 3 (1.5 điểm)
a. Hai bạn Phương và Như đang cùng làm bài tập Toán. Sau một lúc, hai bạn trao đổi kết quả với nhau:
- Bạn Phương nói: “Tớ tìm được tất cả 448 số tự nhiên có bốn chữ số khác nhau chia hết cho 5”.
- Bạn Như lại bảo: “Đáp số của mình là 504 số ”.
Em có đồng ý với đáp số của bạn nào không? Bằng lập luận toán học, hãy giải thích tại sao?
b. Đoàn trường THPT Tây Thạnh đã trao danh hiệu “Học sinh 3 tốt” cho học sinh 3 khối với số
lượng như sau: Khối 12: 4 nam, 2 nữ; Khối 11: 3 nam, 3 nữ; Khối 10: 2 nam, 2 nữ. Hỏi có bao nhiêu
cách chọn 3 học sinh đại diện dự lễ tuyên dương phong trào “Học sinh 3 tốt” cấp Quận sao cho có cả
nam lẫn nữ và có học sinh của 3 khối lớp. Câu 4 (1.0 điểm)
Có 90 viên bi được đánh số từ 1 đến 90. Một người lấy ngẫu nhiên không hoàn lại lần lượt từng viên bi.
Tính xác suất để sau ba lần lấy, người này có ít nhất một viên bi có ghi hai chữ số giống nhau. Câu 5 (3.5 điểm)
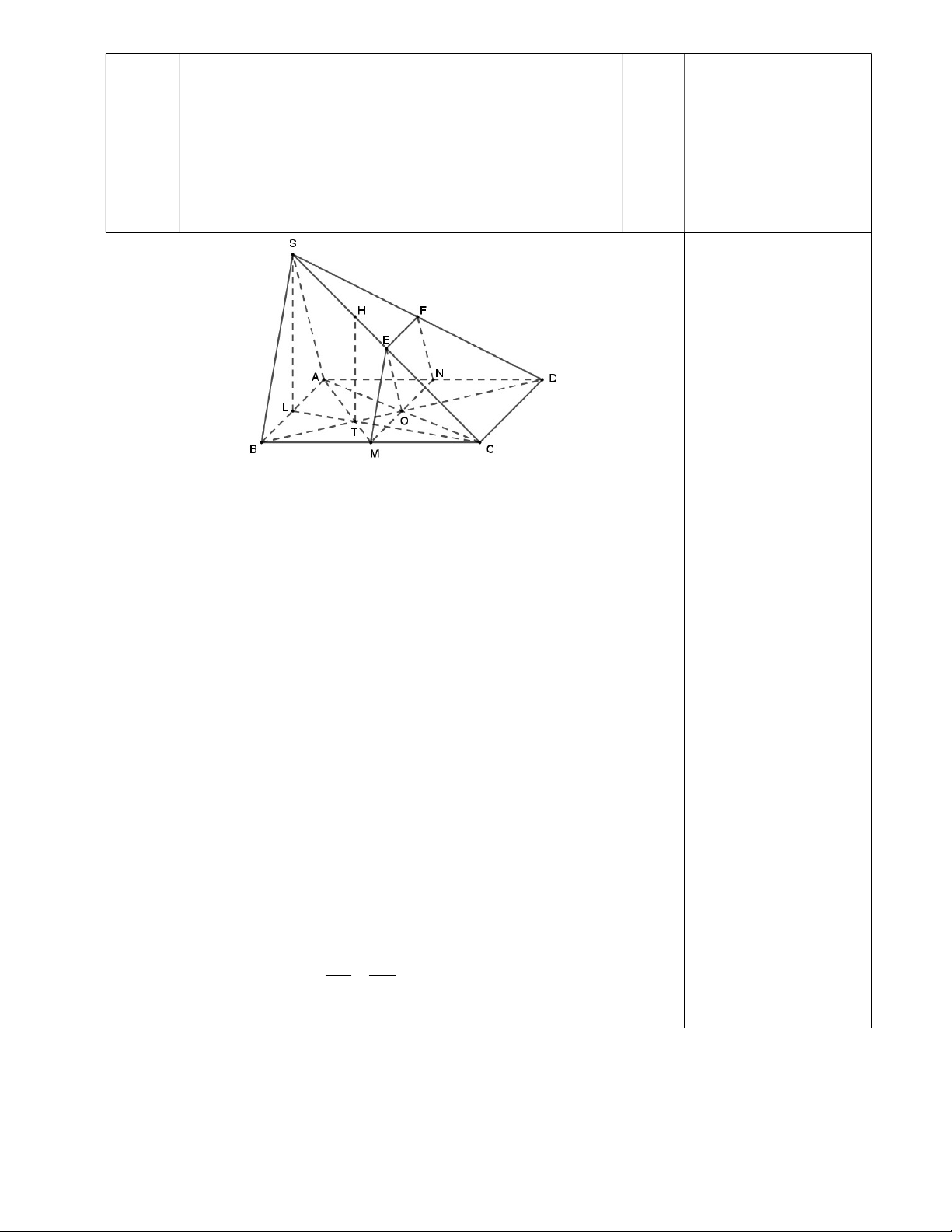
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O . Gọi M , E lần lượt là trung điểm của cạnh BC , SC .
a. Xác định giao tuyến của hai mặt phẳng SAC và SBD.
b. Xác định giao điểm F của đường thẳng SD và mặt phẳng MEO .
c. Chứng minh mặt phẳng MEO song song với mặt phẳng SAB .
d. Gọi T là giao điểm của AM và BD ; điểm H thuộc cạnh SC sao cho SC 3SH . Chứng minh
đường thẳng HT song song với mặt phẳng SAB . -------Hết------
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ I – NĂM HỌC 2019 – 20120 MÔN TOÁN – KHỐI 11 Câu
Lời giải (cần vắn tắt – rõ các bước được điểm) Điểm Lưu ý khi chấm Câu 1 3 a. 3 tan 2x 3 0 tan 2x 7 7 3 2x k 0.5 7 6 13 x k , k 0,5 84 2
b. 3 cos x 2sin 2x sin x 0 sin x 3 cos x 2sin 2x 1 3 sin x cos x sin 2x sin x sin 2x 0,5 2 2 3 x k2 3 , k 0,5 4 2 x k 9 3 c. x x2 sin cos
cos x1 2cos x 51sin x 2
1 2sin x cos x cos x 2cos x 5 5sin x 0 x x 2 cos 1 2sin
2sin x 5sin x 2 0
1 2sin xcos x sin x 2 0 0,25 1 x k2 sin x 6 2 , k 5 0,25 cos x sin x 2 (...) x k2 6 Câu 2 a. 2 2 C A 57P ĐK: n 2, n n 2n 3 n! (2n)! 0,25 57.6 2!.(n 2)! (2n 2)! 2
... 9n 5n 684 0 ... n 9 0,25 10 10 10 2 2 k b. k k x C x 2 10 2 x k 0 x 10 10
C 2 3 20 1 k k k k x 0,5 10 k 0
Theo yêu cầu đề bài, ta có: 3k 20 7 k 9 0,25 Hệ số của 7 x bằng 20 . 0,25
Câu 3 a. Gọi số cần tìm có dạng abcd
Hs có thể trả lời trước TH1: d 0 , a, ,
b c lần lượt có 9,8,7 cách chọn nên có
0,25 là không đồng ý với cả
1.9.8.7 504 số thỏa mãn yêu cầu
0,25 hai bạn, rồi mới giải TH2: d 5, a, ,
b c lần lượt có 8,8, 7 cách chọn nên có thích. 0,25
1.8.8.7 448 số thỏa mãn yêu cầu
Vậy có: 504 448 952 số cần tìm. Không đồng ý với cả 0,25 hai bạn.
b. Số cách chọn 3 học sinh ở 3 khối là: 6.6.4 144 cách 0,5
Số cách chọn 3 học sinh nam ở 3 khối là: 4.3.2 24 cách
Số cách chọn 3 học sinh nữ ở 3 khối là: 2.3.2 12 cách
Vậy số cách chọn thỏa yêu cầu: 144 24 12 108 cách.
Câu 4 Số cách chọn 3 bi tùy ý là n 90.89.88 704880 . 0,25
Gọi biến cố A: “Ba bi được rút có đánh số tạo từ 2 chữ số giống nhau”
Trong 90 viên bi có 8 viên đánh số tạo từ 2 chữ số giống
nhau nên số cách chọn 3 viên bi không có 8 viên trên bằng 82.81.80 nên n( )
A 90.89.88 82.81.80 173520 0,5 173520 241 Vậy P( ) A . 0,25 90.89.88 979 Câu 5
a. S SAC SBD 1 0,25 O AC, AC SAC
O SAC SBD 2 O BD, BD 0,5 SBD Từ
1 ,2 SO SAC SBD. 0,25
b. Chọn SCD chứa SD . E SCD MEO
Ta có: MO MEO,CD SCD MO//CD(...)
MEO SCD (với qua E , //MO//CD ) 0,5 F SD Gọi F SD , 0,25 F SD MEO . F MEO 0,25
ME, MO MEO, ME MO M ME//SB (...) 0,25 c. Ta có: MO//AB (...) 0,25 SB, AB SAB
Vậy MEO // SAB . 0,25
d. Gọi trung điểm L của AB . Ta có: ... LC 3LT 0,25 LC SC Mà SC 3SH nên hay HT //SL . 0,25 LT SH
Mà SL SAB nên HT // SAB 0,25




