Đề thi học kì 1 Toán 11 năm 2019 – 2020 trường THPT Trần Khai Nguyên – TP HCM

SỞ GIÁO DỤC & ĐÀO TẠO TP HCM
ĐỀ THI HKI, KHỐI 11, NĂM HỌC 2019-2020
TRƯỜNG THPT TRẦN KHAI NGUYÊN Môn : TOÁN
Thời gian : 90 phút (không kể thời gian giao đề)
Họ và Tên:………………………………...........Số báo danh:…………………………….Mã đề: 111
Câu 1: [2 điểm] Giải các phương trình             a) 2 2cos x   9cos x  11  0     b) 3 sin 3x   cos 3x   2  7   7       3   3 
Câu 2: [1,5 điểm] Gieo con súc sắc cân đối đồng chất ba lần.
a) Hãy mô tả không gian mẫu và tính số phần tử của không gian mẫu.
b) Tính số phần tử của biến cố “cả ba lần gieo không có lần nào giống nhau”. 1 1 1 1
Câu 3: [1,75 điểm] Cho tổng S     ... với * n   n 1 3 . 3.5 5 7 . 2n   1 2n   1 a) Tính S ,S ,S ? 1 2 3 n
b) Bằng phương pháp quy nạp, hãy chứng minh * S  ,n   ? n 2n 1
Câu 4: [1 điểm] Tìm 3 số hạng liên tiếp của 1 cấp số cộng biết tổng của chúng bằng 27 và tổng các bình
phương của chúng là 293.
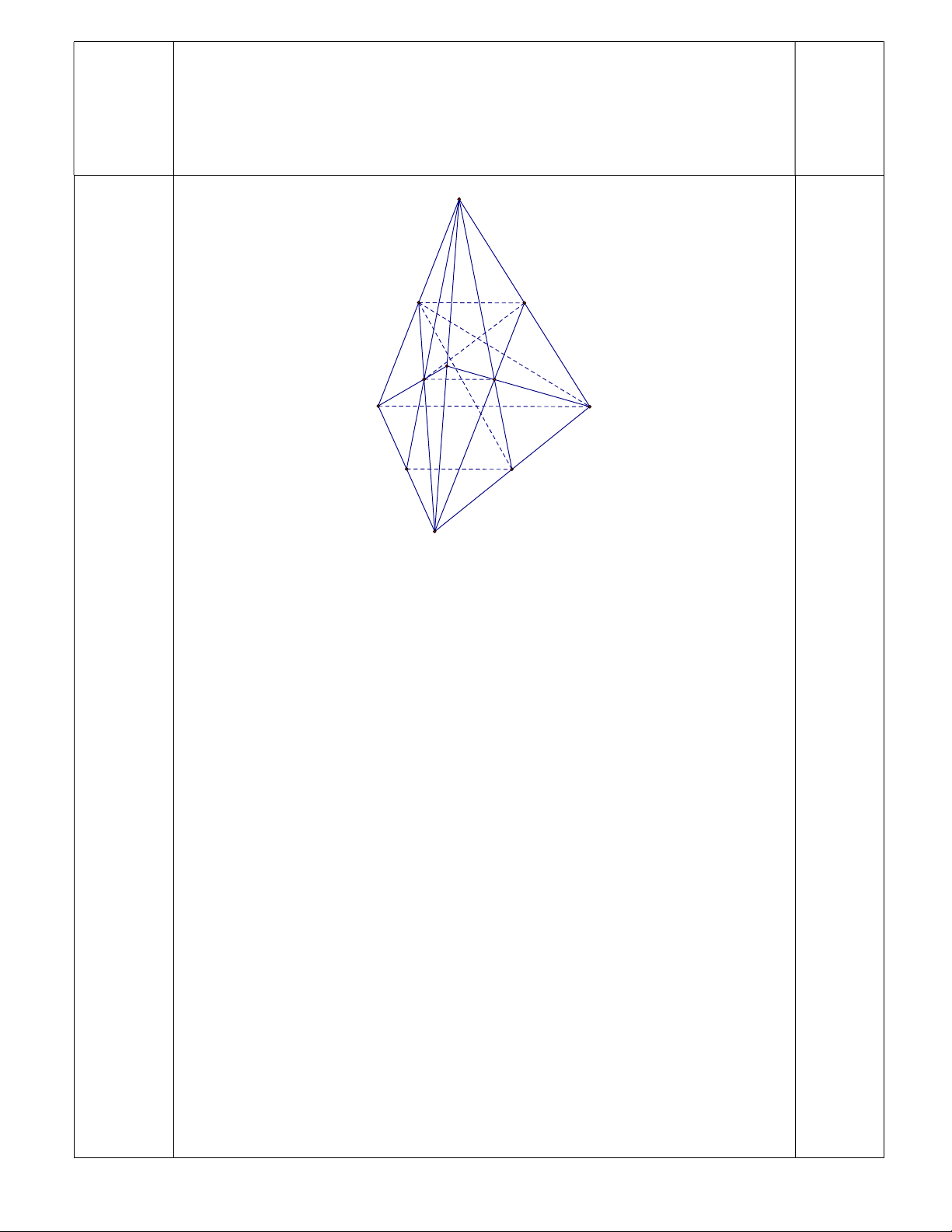
Câu 5: [3 điểm] Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AD là đáy lớn). E , F lần lượt là trung
điểm của SA và SD . Gọi K là giao điểm của các đường thẳng AB và CD .
a) Tìm giao tuyến của (SAB) và (SCD) ; Tìm giao điểm M của đường thẳng SB và CDE .
b) Tìm giao điểm N của đường thẳng SC và EFM . Tứ giác EFNM là hình gì?
c) Chứng minh các đường thẳng AM , DN , SK đồng quy.
Câu 6: [0,75 điểm] Trong mặt phẳng tọa độ Oxy , chọn ngẫu nhiên một điểm có hoành độ và tung độ là những
số nguyên có giá trị tuyệt đối bé hơn 4 . Tính xác suất để chọn được điểm mà khoảng cách từ điểm đó
đến gốc tọa độ không vượt quá 2? HẾT 1
SỞ GIÁO DỤC & ĐÀO TẠO TP HCM
ĐỀ THI HKI, KHỐI 11, NĂM HỌC 2019-2020
TRƯỜNG THPT TRẦN KHAI NGUYÊN Môn : TOÁN
Thời gian : 90 phút (không kể thời gian giao đề)
Họ và Tên:………………………………...........Số báo danh:…………………………….Mã đề: 112
Câu 1: [2 điểm] Giải các phương trình             a) 2 2cos x  3cos x  5  0     b) sin 5x   cos 5x    2  5   5       3   3 
Câu 2: [1,5 điểm] Gieo con súc sắc cân đối đồng chất bốn lần.
a) Hãy mô tả không gian mẫu và tính số phần tử của không gian mẫu.
b) Tính số phần tử của biến cố “cả bốn lần gieo không có lần nào giống nhau”. 1 1 1 1
Câu 3: [1,75 điểm] Cho tổng S     ... với * n   n 1.5 5.9 9.13 4n 34n   1 a) Tính S ,S ,S ? 1 2 3 n
b) Bằng phương pháp quy nạp, hãy chứng minh * S  ,n   ? n 4n 1
Câu 4: [1 điểm] Tìm 3 số hạng liên tiếp của 1 cấp số cộng biết tổng của chúng bằng 18 và tổng các bình
phương của chúng là 140 .
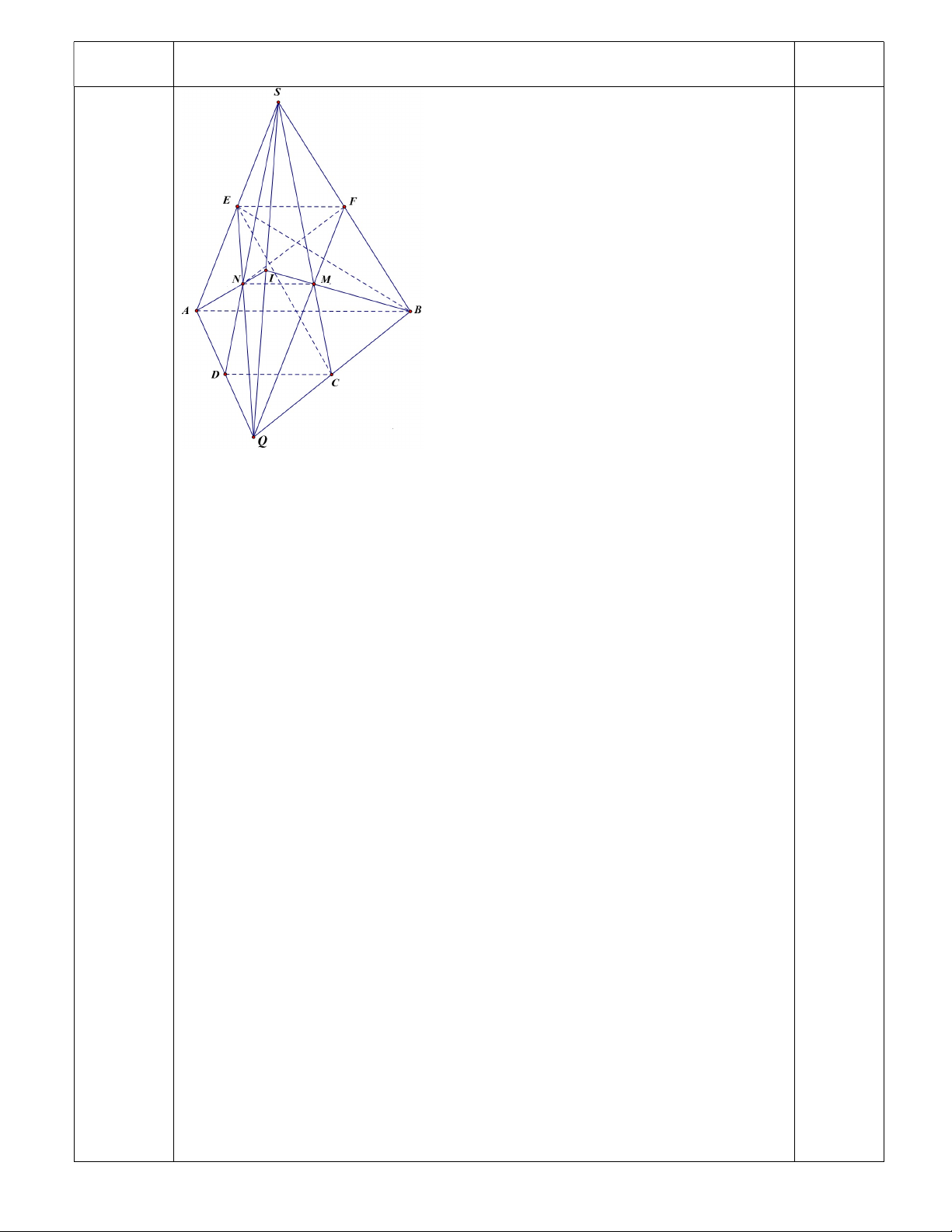
Câu 5: [3 điểm] Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AB là đáy lớn). E , F lần lượt là trung
điểm của SA và SB . Gọi Q là giao điểm của các đường thẳng AD và BC .
a) Tìm giao tuyến của (SAD) và (SBC) ; Tìm giao điểm N của đường thẳng SD và CBE.
b) Tìm giao điểm M của đường thẳng SC và EFN . Tứ giác EFMN là hình gì?
c) Chứng minh các đường thẳng AN , BM , SQ đồng quy.
Câu 6: [0,75 điểm] Trong mặt phẳng tọa độ Oxy , chọn ngẫu nhiên một điểm có hoành độ và tung độ là những
số nguyên dương bé hơn 10 . Tính xác suất để chọn được điểm mà khoảng cách từ điểm đó đến gốc tọa độ không vượt quá 4? HẾT 2
HƯỚNG DẪN CHẤM TOÁN 11_Đề: 111 Câu 1a [A]       Điểm chi Giải phương trình 2 2cos x   9cos x  11  0     .  7   7  tiết (1 điểm)      2  2cos x   9cos x  11  0      7   7     Đặt t  cos x  , 1   t 1   0,25  7  t  1(n)
Khi đó, phương trình trở thành: 2 2t 9t 11 0      11 0,25 t   (l)  2      Với t 1 ta có: cos x 
1  x   k2 ,k   x   k2,k     0,5  7  7 7  Vậy x   k2 , k  7 Câu 1b [A]       Điểm chi
Giải phương trình: 3 sin 3x   cos 3x   2     .  3   3  tiết (1 điểm)       3 sin 3x   cos 3x   2      3   3       2sin 3x    2    3 6      sin 3x   1    2  0,5    3x    k2 2 2 0,25  k2  x   k    3 3  k2
Vậy phương trình đã cho có nghiệm x   k    3 3 0,25
Câu 2 [A] Gieo con súc sắc cân đối đồng chất ba lần. Điểm chi
a) Hãy mô tả không gian mẫu và tính số phần tử của không gian mẫu. tiết
b) Tính số phần tử của biến cố “cả ba lần gieo không có lần nào giống nhau”.
(1,5 điểm) a) Không gian mẫu   
 i; j;k i, j,k 1,2,...,  6  n 3  6  216 . 0,75
b) Biến cố A : “Cả ba lần gieo không có lần nào giống nhau” có số phần tử là 0,75 n A 3
 A 120 . (phải có giải thích) 6 Câu 3 [A] 1 1 1 1 Cho tổng S     ... với * n   Điểm chi n 1 3 . 3 5 . 5.7 2n   1 2n   1 (1,75 điểm) tiết a) Tính S ,S ,S ? 1 2 3 n
b) Bằng phương pháp quy nạp, hãy chứng minh * S  ,n   ? n 2n 1 1 1 a) S   0,25 1 1 3 . 3 3 1 1 2 0,25 S    2 1 3 . 3.5 5 1 1 1 3 S     3 0,25 1 3 . 3.5 5.7 7 n b) Ta chứng minh * S  , n    n   1 2n 1 1 1
Với n  1, ta có: S   1 3 2.11
Suy ra (1) đúng với n  1. k
Giả sử (1) đúng với n  k  1, nghĩa là S  . 0,25 k 2k 1
Ta cần chứng minh (1) đúng với n  k 1, nghĩa là chứng minh k 1 k 1 S   2 k 1  2k     1 1 2k  3 0,25 Thật vậy, ta có 1 1 1 1 1 S     ...  k 1  1.3 3.5 5.7 2k  12k   1 2k   1 2k  3 1  S  k  2k   1 2k  3 k 1   2k 1 2k   1 2k  3 k 2k  3 2 1 2k  3k 1    2k   1 2k  3 2k   1 2k  3 2k  1k  1 k 1    2k   1 2k  3 2k  3 0,25  (2) đúng n Vậy * S  ,n   (đpcm) 0,25 n 2n 1
Câu 4 [A] Tìm 3 số hạng liên tiếp của 1 cấp số cộng biết tổng của chúng bằng 27 và tổng các Điểm chi
bình phương của chúng là 293. tiết (1 điểm)
Gọi 3 số hạng liên tiếp của cấp số cộng: u ;u ;u . Theo đề bài ta có: 1 2 3 u   u  u  27 1  1 2 3    2 2 2 u   u  u  293 2  1 2 3   0,25
 1  u u  d u  2d  27  3u  3d  27  d  9u . 1 1 1 1 1
2  u  u  d 2  u  2d 2 2  293 1 1 1
 u  u  9  u 2  u 18  2u 2  293  u  81 18  u 2 2 2  293 0,25 1 1 1 1 1 1 1 u 14 2 1  2u 36u 112  0  1 1 u  4  0,25 1
Với u  14  d  5  u  9;u  4. 1 2 3
Với u  4  d  5  u  9;u  14. 1 2 3 0,25
Câu 5 [A] Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AD là đáy lớn). E , F lần Điểm chi
lượt là trung điểm của SA và SD . Gọi K là giao điểm của các đường thẳng AB và tiết CD . 4
a) Tìm giao tuyến của (SAB) và (SCD) ; Tìm giao điểm M của đường thẳng SB và CDE.
b) Tìm giao điểm N của đường thẳng SC và EFM . Tứ giác EFNM là hình gì?
c) Chứng minh các đường thẳng AM , DN , SK đồng quy. S E F I N M A D B C K
a) Tìm giao tuyến của (SAB) và (SCD) . Tìm giao điểm M của đường thẳng SB và (1,25 điểm) CDE . SSAB  (SCD) 0,25
K  AB, AB  SAB  K SAB 
  K SAB SCD 0,25
K  CD,CD  SCD  K SCD
Vậy SAB SCD  SK 0,25
Trong (SAB), gọi M  SB  EK 0,25 M SB  
M  EK, EK  CDE  M CDE  M  SB  CDE 0,25
_____________________________________________________________________ ________ b) Cách 1: (1 điểm) M MEF  
M SB, SB  SBC  M SBC 0,25
 M MEF SBC d  (EFK)  (SBC) 
EF/ / BC (EF / /AD, BC / /AD)  d / / EF/ / BC  0,25 EF  (EFK), BC  (SBC)  0,25
Trong (SBC) gọi N  d  SC  N  SC  MEF  0,25
Vì d / / EF  MN/ / EF nên tứ giác EFNM là hình thang.
____________________________________________________________________ _______
Cách 2: Trong (SCD), gọi N  KF SC 5 N SC  0,25 
N  KF, KF  EFM  N EFM .  N  SC  EFM
Chứng minh MN  (EFK)  (SBC) 0,25 MN  (EFK)  (SBC) 
Có EF  BC (EF / /AD, BC / /AD)  MN  EF  BC . 0,25 EF  (EFK),BC  (SBC)  0,25
Suy ra tứ giác EFNM là hình thang. _______
_________________________________________________________________
c) Chứng minh các đường thẳng AM, DN, SK đồng quy
Ta có: MN / /AD (cùng song song với BC)
(0,75 điểm) Trong mp(ADNM), gọi I  AM  DN .      I AM, AM (SAB) I (SAB) 
I CD,CD  (SCD)  I (SCD)  I  (SAB)  (SCD) 0,25
Mà SAB SCD  SK  ISK . 0,25
Vậy 3 đường thẳng AM, DN, SK đồng quy tại điểm I. 0,25
Câu 6 [A] Trong mặt phẳng tọa độ Oxy , chọn ngẫu nhiên một điểm có hoành độ và tung độ là Điểm chi
những số nguyên có giá trị tuyệt đối bé hơn 4 . Tính xác suất để chọn được điểm mà tiết
khoảng cách từ điểm đó đến gốc tọa độ không vượt quá 2? (0,75 điểm)  x  4 
Gọi M  x; y là điểm thỏa mãn x, y  và   y  4  x    3  ; 2  ;1;0 1 ; ;2;  3    y    3  ; 2  ; 1  ;0 1 ; ;2;  3
Do đó có 7 cách chọn hoành độ, 7 cách chọn tung độ cho điểm M nói trên.
Theo quy tắc nhân, n  7 7 .  49 0,25
Gọi A: “Chọn được điểm mà khoảng cách từ điểm đó đến gốc tọa độ không vượt quá 2”
Gọi M '  x'; y'  là điểm thỏa x', y'   và OM  2 . 2 2 2 2
OM  2  x'  y'  2  x'  y'  4  x' 0; 1  ;  2
TH1: x'  0  y' 0; 1  ;  2
Theo QT nhân, có 1.5  5 cách thỏa TH1. TH2: x'  1   y' 0;  1 Theo QT nhân, có 2 3 .  6 cách thỏa TH2. TH3: x'  2  y'  0 Theo QT nhân, có 2 1 .  2 cách thỏa TH3.
Theo QT cộng, n A  5  6  2 13 0,25 0,25  P A n A 13   n 49 6
HƯỚNG DẪN CHẤM TOÁN 11_ĐỀ 112 Câu 1a [B]       Điểm chi Giải phương trình 2 2cos x  3cos x  5  0     .  5   5  tiết (1 điểm)      2  2cos x  3cos x  5  0      5   5     Đặt t  cos x  , 1   t 1    5  t  1(n)
Khi đó, phương trình trở thành: 2 2t 3t 5 0      5 t  (l)  2     4 Với t  1  ta có: cos x   1
  x     k2,k   x   k2 ,k      5  5 5 4 Vậy x   k2 ,k  5 Câu 1b [B]       Điểm chi
Giải phương trình: sin 5x   cos 5x    2     .  3   3  tiết (1 điểm)       sin 5x   cos 5x    2      3   3       2 sin 5x     2    3 4   7   sin 5x   1     12  7   5x     k2 12 2 13 k2  x    k    60 5 13 k 2
Vậy phương trình đã cho có nghiệm x    k    60 5
Câu 2 [B] Gieo con súc sắc cân đối đồng chất bốn lần. Điểm chi
a) Hãy mô tả không gian mẫu và tính số phần tử của không gian mẫu. tiết
b) Tính số phần tử của biến cố “cả bốn lần gieo không có lần nào giống nhau”.
(1,5 điểm) a) Không gian mẫu   
 i; j;k;l i, j,k,l 1,2,...,  6  n 4  6 1296 .
b) Biến cố A : “Cả bốn lần gieo không có lần nào giống nhau” có số phần tử là n A 4  A  360 . 6 Câu 3[B] 1 1 1 1 Cho tổng S     ... với * n   Điểm chi n 1.5 5.9 9.13 4n 34n   1 tiết a) Tính S ,S ,S ? 1 2 3 n
b) Bằng phương pháp quy nạp, hãy chứng minh * S  ,n   ? n 4n 1 (1,75 điểm) 1 1 S   1 a) 1.5 5 7 1 1 2 S    2 1 5 . 5.9 9 1 1 1 3 S     3 1.5 5.9 9.13 13 n b) Ta chứng minh * S  , n    n   1 4n 1 1 1
Với n  1, ta có: S   1 5 4.11
Suy ra (1) đúng với n  1. k
Giả sử (1) đúng với n  k  1, nghĩa là S  . k 4k 1
Ta cần chứng minh (1) đúng với n  k 1, nghĩa là chứng minh k 1 k 1 S   2 k 1  4k     1 1 4k  5 Thật vậy, ta có 1 1 1 1 1 S     ...  k 1  1 5 . 5.9 9.13
4k 34k  1 4k   1 4k  5 1  S  k 4k   1 4k  5 k 1   4k 1 4k   1 4k  5 k 4k  5 2 1 4k  5k 1    4k   1 4k  5 4k   1 4k  5 4k   1 k   1 k 1    4k   1 4k  5 4k  5  (2) đúng n Vậy * S  ,n   (đpcm) n 4n 1 Câu 4[B]
Tìm 3 số hạng liên tiếp của 1 cấp số cộng biết tổng của chúng bằng 18 và tổng các Điểm chi
bình phương của chúng là 140 tiết (1 điểm)
Gọi 3 số hạng liên tiếp của cấp số cộng: u ; u ; u . Theo đề bài ta có: 1 2 3 u  u  u   18 1 1 2 3    2 u  2 u  2 u   140 2 1 2 3  
 1  u  u d  u  2d  27  3u  3d  18  d  6  u . 1 1 1 1 1 2  u  u d u 2d 140 1   1 2   1 2 2   u  u 6 u u 12 2u 140 u 36 12 u 140 1    1 1 2     1 1 2     1   12 2 2   2
2u  24u  40  0  u  10  u  2 1 1 1 1
Với u  10  d  4  u  6; u  2. 1 2 3
Với u  2  d  4  u  6; u  10. 1 2 3 Câu 5[B]
Cho hình chóp S.ABCD có đáy ABCD là hình thang ( AB là đáy lớn). E , F lần lượt Điểm chi
là trung điểm của SA và SB . Gọi Q là giao điểm của các đường thẳng AD và BC . tiết
a) Tìm giao tuyến của (SAD) và (SBC) ; Tìm giao điểm N của đường thẳng SD và CBE.
b) Tìm giao điểm M của đường thẳng SC và EFN . Tứ giác EFMN là hình gì? 8
c) Chứng minh các đường thẳng AN , BM , SQ đồng quy. (3 điểm)
a) Tìm giao tuyến của (SAD) và (SBC) . Tìm giao điểm N của đường thẳng SD và CBE SSAD  (SBC)
Q  AD, AD  SAD  QSAD QSADSBC
Q  BC, BC  SBC  QSBC 
Vậy SAD SBC  SQ
Trong (SAD), gọi N  SD  EQ N SD  
N  EQ, EQ  CBE  M CBE  N  SD  CBE
b) Trong (SBC), gọi M  QF SC M SC  
M  QF, QF  EFN  M EFN.  M  SC  EFN
Chứng minh MN  (EFQ)  (SDC) MN  (EFQ)  (SDC) 
Có EF/ /DC (EF / /AB, CD / /AB)  MN / / EF/ /DC . EF  (EFN),DC  (SDC) 
Suy ra tứ giác EFMN là hình thang.
c) Chứng minh các đường thẳng AN, BM, SQ đồng quy.
Ta có: MN / /AB (cùng song song với CD)
Trong (ABMN), gọi I  AN  BM .
I  AN,AN  (SAD)  I(SAD) 
I  BM,BM  (SBC)  I(SBC)  I  (SAD)  (SBC)
Mà SAD SBC  SQ  I SQ .
Vậy 3 đường thẳng AN, BM, SQ đồng quy tại điểm I. 9
Câu 6 [B] Trong mặt phẳng tọa độ Oxy , chọn ngẫu nhiên một điểm có hoành độ và tung độ là Điểm chi
những số nguyên dương bé hơn 10 . Tính xác suất để chọn được điểm mà khoảng tiết
cách từ điểm đó đến gốc tọa độ không vượt quá 4? (0,75 điểm) x  10
Gọi M  x; y là điểm thỏa mãn * x, y   và   y  10 x   1;2;3;4;5;6;7;8;  9   y   1;2;3;4;5;6;7;8;  9
Do đó có 9 cách chọn hoành độ, 9 cách chọn tung độ cho điểm M nói trên.
Theo quy tắc nhân, n  9 9 .  81
Gọi A: “Chọn được điểm mà khoảng cách từ điểm đó đến gốc tọa độ không vượt quá 4”
Gọi M '  x'; y'  là điểm thỏa x', y'   và OM  4 . 2 2 2 2
OM  4  x'  y'  4  x'  y'  16  x' 1;2;  3 TH1: x' 1;  2  y' 1;2;  3 Theo QT nhân, có 2 3 .  6 cách thỏa TH1.
TH2: x'  3  y' 1;  2
Theo QT nhân, có 1.2  2cách thỏa TH2.
Theo QT cộng, n  A  6  2  8  P  A n A 8   n 81 10