Đề thi học kì 1 Toán 11 năm 2021 – 2022 trường THPT Nguyễn Thị Minh Khai – TP HCM

Đề 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HCM ĐỀ KIỂM TRA HỌC KÌ I
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI Năm học: 2021 – 2022 Môn TOÁN – Khối: 11 Thời gian: 90 phút
(Không kể thời gian phát đề)
Họ tên học sinh: …………………………………………………… SBD: ……………………………
Bài 1: Giải các phương trình a) 2
2cos x  5cos x  3  0. (1 điểm)
b) sin x  4sin 2x  sin 3x  0. (1 điểm)
Bài 2: Chọn ngẫu nhiên 3 số tự nhiên khác nhau từ tập A  1;2;3;...;8 
0 . Tính xác suất để trong
3 số được chọn có đúng 2 số là số chính phương. (1 điểm) 7  1 
Bài 3: Tìm hệ số của số hạng chứa 4
x trong khai triển nhị thức Newton của 2  2x  với x  0. 3   x  (1 điểm)
Bài 4: Dùng phương pháp qui nạp toán học, chứng minh rằng với mọi số nguyên dương n ta luôn có 2n 1 u 3  
1 chia hết cho 4. (1 điểm) n u   u 10 1 3
Bài 5: Tìm số hạng đầu tiên u và công sai d của cấp số cộng   n u  biết  . (1 điểm) 1 41 u   u  2 5  2
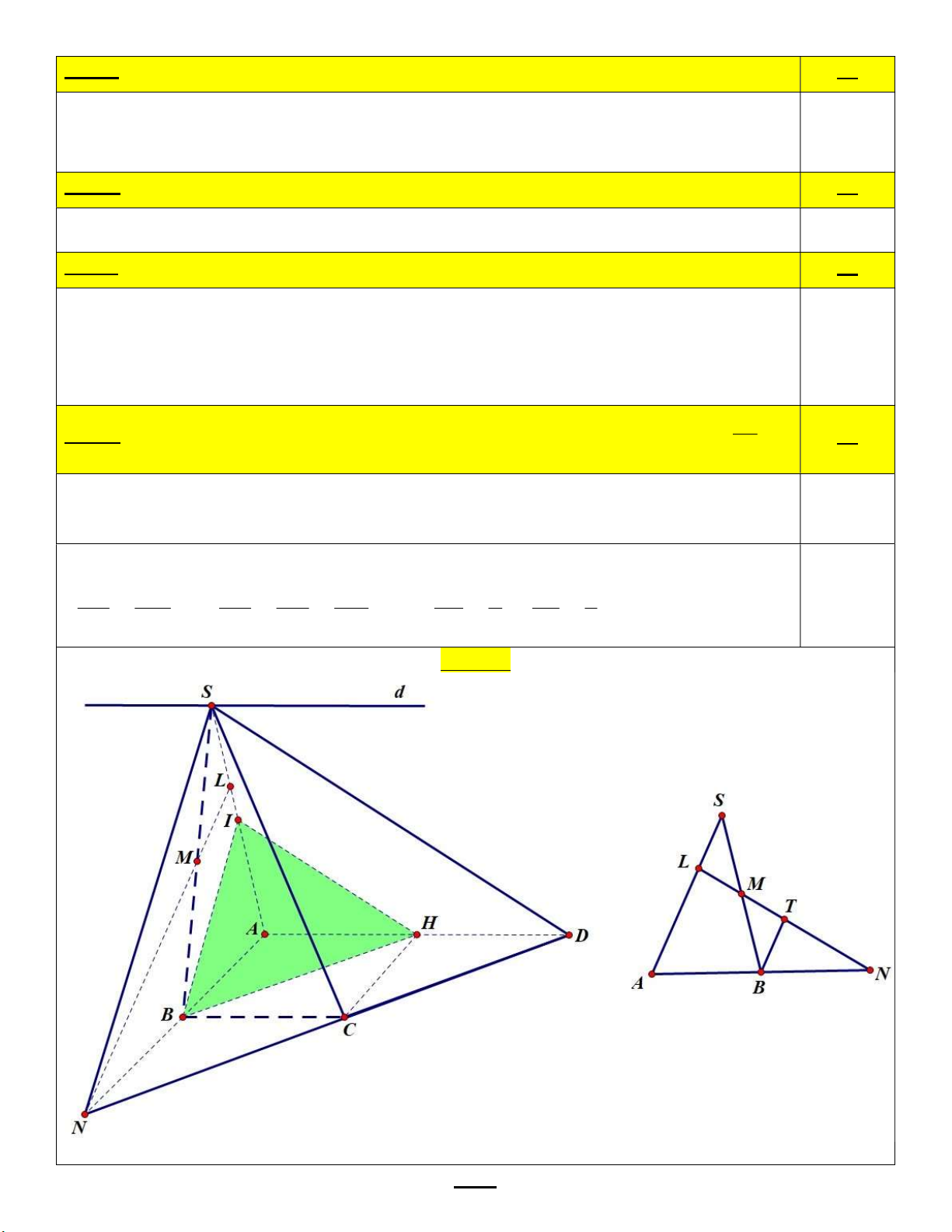
Bài 6: Cho hình chóp S.ABCD có mặt đáy ABCD là hình thang, cạnh đáy lớn AD  2BC . Gọi
H là trung điểm của AD , I là trung điểm của SA.
a) Tìm giao tuyến của hai mặt phẳng SAD và SBC. (1 điểm)
b) Chứng minh rằng đường thẳng CH song song với mặt phẳng SAB. (1 điểm)
c) Chứng minh rằng mặt phẳng BIH  song song với mặt phẳng SCD. (1 điểm)
d) Gọi M là trung điểm của SB , đường thẳng SA cắt mặt phẳngMCD tại L. Tính tỉ số SL . (1 điểm) SA HẾT
ĐÁP ÁN & BIỂU ĐIỂM ĐỀ 2 Bài 1a: 2
2cos x  5cos x  3  0 (1) 1đ   cos x  3 (l) x   k2     3 1  1   k   0.25x4 cos x      2 x   k2  3
Bài 1b: sin x  4sin 2x  sin 3x  0 (1) 1đ   sin 2x  0  1  2sin 2 .
x cos x  4sin 2x  0    x  k k  0.25x4 cos x  2  l 2
Bài 2: Chọn ngẫu nhiên 3 số tự nhiên khác nhau từ tập A  1;2;3;...;8  0 . Tính xác suất 1đ
để trong 3 số được chọn có đúng 2 số là số chính phương.
 Số cách chọn 3 số từ 80 số là: n  3 C  80 82160.
 Từ 1 đến 80 có 8 số chính phương và có 80 8  72 số không chính phương. 0.25x4  Do đó:    2 1 .C  2016  126 n A C8 72 PA  5135 7  1 
Bài 3: Tìm hệ số của số hạng chứa 4
x trong khai triển nhị thức Newton của 2 2x   1đ 3 x    k 7k  1  Số hạng tổng quát: . 2 2  7 .  .2  . 1 k k k k  .  k C x C x  3    14 5 7 7  x  0.25x4 Số hạng chứa 4
x khi 14  5k  4  k  2.
Hệ số của số hạng chứa 4 x là C .2 . 2 2 5 1  672. 7
Bài 4: Dùng qui nạp, chứng minh rằng với mọi số nguyên dương n ta luôn có 2n 1 1đ u 3   1 chia hết cho 4. n
 n = 1: u  3 1 44, mệnh đề đúng khi n = 1 1  Giả sử ta có 2k 1 u 3   14  * k   k Ta cần chứng minh: 2k 1 u  3   14 0.25x4 k 1  Thật vậy: 2k 1  2k 1  2k 1  2k 1  2k 1 u  3  1 9.3 1  3  1  8.3  u  8.3  4 k 1  k
 Theo nguyên lí qui nạp: ta có đpcm. u  u 10 1 3  Bài 5: .  41 1đ u  u 2 5   2    u  u  2d 10 2u  2d 10  3  1  1   1  u  1       2   41   41   0.25x4  u  d  u  4d  2u 5d   7 1   1   2 1  2 d   2
Bài 6a: Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC). 1đ
S SADSBC 
SADSBC d qua S;d / /AD / /BC. 0.25x4 AD / /  BC
Bài 6b: Chứng minh CH//(SAB). 1đ
Chứng minh ABCH là hình bình hành  CH / / AB, AB SAB  CH / /SAB. 0.25x4
Bài 6c: Chứng minh (BIH)//(SCD). 1đ
 Chứng minh IH //SD (đường trung bình trong SAD).
 Chứng minh BHDC là hình bình hành  BH / /CD . 0.25x4  Suy ra (BIH)//(SCD). SL
Bài 6d: M trung điểm SB, đường thẳng SA cắt mặt phẳng (MCD) tại L. Tính tỉ số . 1đ SA
Trong (ABCD), gọi N là giao điểm của CD và AB. 0.5
Trong (SAB), gọi L là giao điểm của MN và SA. Suy ra L là giao điểm của SA và (MCD).
Từ B kẻ BT//SA, T thuộc MN SL SM LA NA AD SL 1 SL 1 0.5  1;    2     . BT MB BT NB BC LA 2 SA 3 Hình vẽ HẾT