Đề thi học kỳ 1 môn Toán 11 Quảng Nam 2019-2020 (có đáp án)

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ I NĂM HỌC 2019-2020 QUẢNG NAM
Môn: TOÁN – Lớp 11
Thời gian: 60 phút (không kể thời gian giao đề) ĐỀ CHÍNH THỨC
(Đề gồm có 02 trang) MÃ ĐỀ 102
A. TRẮC NGHIỆM: (5,0 điểm)
Câu 1. Tìm tập giá trị T của hàm số y = 2cos x + 3.
A. T = [3;5]. B. T = [ 1; - ] 1 . C. T = [ 2; - 2].
D. T = [1;5] .
Câu 2. Chọn ngẫu nhiên một số từ tập X = {1; 2;3; 4;5;6;7;8;9} . Gọi A là biến cố: “số được chọn là
số bé hơn 6”. Khi đó xác suất P( ) A bằng 1 2 5 4 A. . B. . C. . D. . 2 5 9 9
Câu 3. Tìm tất cả các giá trị thực của tham số m để phương trình sin x = m vô nghiệm. A. m Î(- ; ¥ - )
1 . B. m Î(1;+¥) . C. m Î(- ; ¥ - )
1 È (1;+¥) . D. m Î[ 1; - ] 1
Câu 4. Một hộp đựng 6 quả cầu xanh và 7 quả cầu vàng (Các quả cầu có bán kính khác nhau). Hỏi có
bao nhiêu cách chọn ra 3 quả cầu cùng màu từ hộp trên? A. 330. B. 700. C. 58. D. 55.
Câu 5. Cho hai số tự nhiên k, n thỏa 1 £ k £ n . Mệnh đề nào sau đây đúng ? - - k n! k n! k k!(n k)! n k A. C = . B. C = . C. C = k ( )! . D. C = . n (n - k)! n
k!(n - k)! n n! n n!
Câu 6. Trong không gian cho đường thẳng a và mặt phẳng (a) song song với nhau. Phát biểu nào sau đây sai?
A. Trong mặt phẳng (a ) có duy nhất một đường thẳng chéo nhau với đường thẳng a .
B. Có duy nhất một mặt phẳng chứa đường thẳng a và song song với (a ) .
C. Nếu một mặt phẳng (b ) chứa đường thẳng a và cắt (a) theo giao tuyến b thì b song song với a .
D. Trong mặt phẳng (a) có vô số đường thẳng song song với đường thẳng a . 1
Câu 7. Tìm tập xác định của hàm số y = sin . x A. D = ! \ { } 0 .
B. D = ! . C. D = ! \ {kp | k Î Z}. D. D = (0; +¥) .
Câu 8. Trong khai triển biểu thức 10
(3x +1) , hệ số của số hạng chứa 3 x là A. 120
B. 262440 C. 2187 D. 3240
Câu 9. Trong không gian cho tứ diện ABCD . Cặp đường thẳng nào sau đây chéo nhau?
A. AC và BC. B. AB và . CD C. AD và . CD D. AB và . BD !!!"
Câu 10. Trong mặt phẳng cho hình bình hành ABCD . Phép tịnh tiến theo vectơ BC biến điểm A
thành điểm nào sau đây? A. C. B. . D C. . B D. . A Trang 1
Câu 11. Từ tập hợp X = {1; 2;3; 4;5;6;7;8} lập được bao nhiêu số tự nhiên chẵn có 4 chữ số đôi một
khác nhau đồng thời luôn có mặt hai chữ số 1,2 và hai chữ số này đứng cạnh nhau? A. 60. B. 160. C. 90. D. 112.
Câu 12. Gọi x là nghiệm âm lớn nhất của phương trình sin 7x + 3 cos5x = sin 5x + 3 cos7x . Mệnh 0
đề nào sau đây đúng? é p p ö é p ö é p p ö é p ö A. x Î - ;- . B. x Î - ;0 . C. x Î - ;- . D. x Î p - ;- . 0 ê ÷ ê ÷ ê ÷ ê ÷ ë 6 24 ø 0 ë 24 ø 0 ë 3 6 ø 0 ë 3 ø
Câu 13. Trong mặt phẳng với hệ tọa độ Oxy , cho điểm A(0;2) . Tìm tọa độ điểm A' là ảnh của điểm A
qua phép quay tâm O , góc quay 0 90 . A. A'(2;0). B. A'( 2 - ;0). C. A'(0; 2 - ). D. A'(-2;2).
Câu 14. Một công ty nhận được 30 hồ sơ xin việc của 30 người khác nhau muốn xin việc vào công ty,
trong đó có 16 người biết tiếng Anh, 10 người biết tiếng Pháp và 10 người không biết cả tiếng Anh và
tiếng Pháp. Công ty cần tuyển 5 người biết ít nhất một thứ tiếng Anh hoặc Pháp. Tính xác suất để trong
5 người được chọn có 3 người biết cả tiếng Anh và tiếng Pháp? 91 91 455 5 A. . B. . C. . D. . 7752 3289 3876 3876
Câu 15. Trong mặt phẳng với hệ tọa độ Oxy , cho đường thẳng d : x + y - 3 = 0 và đường tròn
(C) (x + )2 + ( y + )2 : 6 8
= 32.Có tất cả bao nhiêu cặp điểm M , N thỏa: !!!!" !!!" "
M Î d, N Î (C): 3OM + ON = 0 ? A. 2. B. 1. C. 0. D. 3.
B. TỰ LUẬN: (5 điểm)
Câu 1 (2 điểm). Giải các phương trình sau: 1
a) cos x = b) 2
3tan x - 4 tan x +1 = 0 2
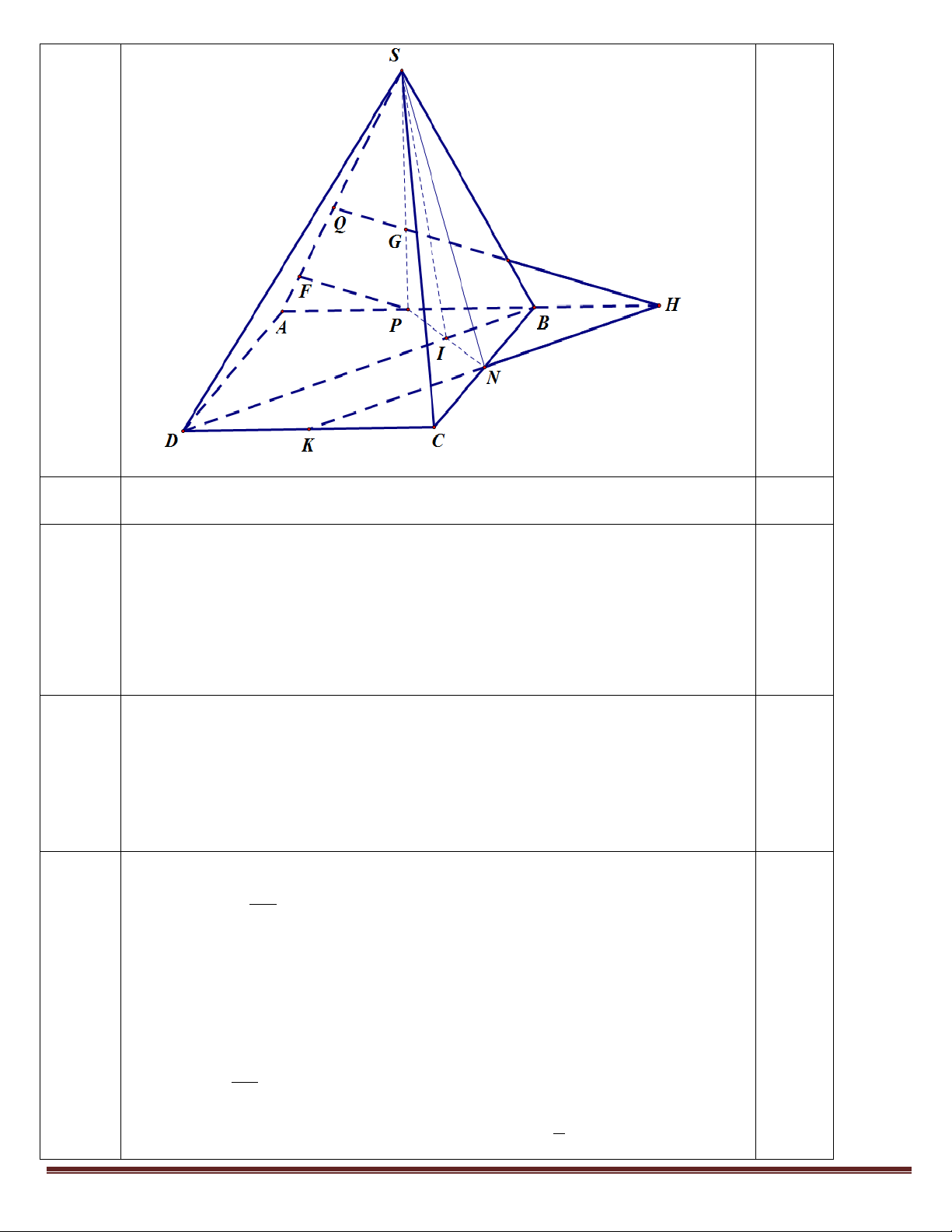
Câu 2 (2,25 điểm). Cho hình chóp S.ABCD có đáy là hình bình hành, G là trọng tâm tam giác SAB ,
N là trung điểm của BC.
a) Chứng minh BC / / (SAD).
b) Tìm giao tuyến của hai mặt phẳng (SGN ) và (SBD). SQ
c) Gọi (a) là mặt phẳng chứa GN và song song với BD , (a) cắt SA tại Q . Tính tỉ số . SA
Câu 3 (0.75 điểm) Một thầy giáo có 18 quyển sách khác nhau gồm 6 quyển sách Toán, 7 quyển sách Lí
và 5 quyển sách Hóa. Thầy chọn ra 9 quyển sách để tặng cho học sinh. Hỏi thầy giáo đó có bao nhiêu
cách chọn sao cho số sách còn lại của thầy có đủ 3 môn?
………………………HẾT…………………… Trang 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KIỂM TRA HỌC KỲ I – NĂM HỌC 2019-2020 QUẢNG NAM
Môn TOÁN – Lớp 11 HƯỚNG DẪN CHẤM
(Hướng dẫn chấm có 9 trang)
A/ TRẮC NGHIỆM: (5,0 điểm) (Mỗi câu đúng được 1/3 điểm) Câu Mã đề 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Mã 102 D C C D B A A D B B C B B C A B. TỰ LUẬN: ( 5 điểm) 2. MÃ ĐỀ 102 Câu 1 (2,0 điểm)
Giải các phương trình sau: a. 1 cos x = b. 2
3tan x - 4 tan x +1 = 0 2 1 p
cos x = Û cos x = cos 0,25 2 3 a) p 1,0đ
Û x = ± + k2p (với k Î ! ). 3 0,75
(Thiếu k Î ! , không có ý 1 mà đúng vẫn cho điểm tối đa; nếu đúng một
trong hai họ nghiệm thì cho 0,5 điểm ) étan x =1 2
3tan x 4 tan x 1 0 ê - + = Û 1 0,5 êtan x = ë 3 b) é p 1,0đ x = + kp ê 4 Û ê , k Î ! 1 0,5
êx = arctan + kp êë 3
(Thiếu k Î ! vẫn cho điểm tối đa) Câu 2. (2.25 đ)
Cho hình chóp S.ABCD có đáy là hình bình hành, G là trọng tâm tam giác SAB , N là trung điểm của BC.
a) Chứng minh BC / / (SAD).
b) Tìm giao tuyến của hai mặt phẳng (SGN ) và (SBD). SQ
c) Gọi (a ) là mặt phẳng chứa GN và song song với BD , (a ) cắt SA tại Q . Tính tỉ số . SA Trang 3 Hình vẽ 0,25 Ghi chú:
Học sinh vẽ đúng hình chóp S.ABCD phục vụ đến câu a thì được 0,25đ
Chứng minh BC / / (SAD). ìBC / / AD a) ï í D A Ì ( D SA ) 0,5 0,75đ ï BC Ë î ( D SA ) Þ BC / / ( D SA ). 0,25
Tìm giao tuyến của hai mặt phẳng (SGN ) & (SBD).
- Có S là điểm chung thứ nhất. b)
- Gọi P là trung điểm AB và I là giao điểm của PN và BD, suy ra I là điểm 0,25
0,75đ chung thứ hai. 0,25
- Kết luận: SI là giao tuyến của hai mặt phẳng (SGN ) & (SBD). 0,25
Gọi (a ) là mặt phẳng chứa GN và song song với BD , (a ) cắt SA tại SQ
Q . Tính tỉ số . SA + Tìm Q .
- Trong (ABCD), kẻ đường thẳng qua N, song song với BD lần lượt cắt CD, c) AB tại K, H. 0,25 0,5đ
- Trong (SAB), kẻ đường thẳng HG cắt SA tại Q thì Q là giao điểm của SA và (a ) . SQ + Tính tỉ số . SA 1
- Tứ giác HBDK là hình bình hành nên HB = DK = . AB 2 Trang 4 - Kẻ PF song song HQ ( SQ SG AF AP F Î 2 1 SA ), ta có: = = ; = = SF SP 3 AQ AH 3 x x x SQ
- Giả sử: QF = x 7 4
Þ SQ = 2x,AF = Þ SA = 2x+ x+ = Þ = . 0,25 2 2 2 SA 7 Câu 3: (0.75 điểm)
Một thầy giáo có 18 quyển sách khác nhau gồm 6 quyển sách Toán, 7 quyển sách Lí và 5
quyển sách Hóa. Thầy chọn ra 9 quyển sách để tặng cho học sinh. Hỏi thầy giáo đó có bao
nhiêu cách chọn sao cho số sách còn lại của thầy có đủ 3 môn?
+ Số cách chọn 9 quyển sách bất kì từ 18 quyển sách bằng: 9 C = 48620 18 0,25
+ Gọi x là số cách thầy giáo chọn sách tặng học sinh sao cho số sách còn lại
không đủ cả 3 môn ( đồng nghĩa thầy giáo tặng hết một loại sách) 6 3 7 2 5 4
x = C .C + C .C + C .C = 990 0,25 6 12 7 11 5 13
+ Suy ra số cách chọn sao cho số sách còn lại của thầy có đủ 3 môn bằng: 9 C - x = 47630 0,25 18
………………………HẾT…………………… Trang 5