Đề thi học kỳ 1 môn Toán lớp 11 năm học 2024 - 2025 - Đề số 1 | Bộ sách Kết nối tri thức

Câu 1:  Chọn mệnh đề đúng trong các mệnh đề sau?  Câu 7: Trong mặt phẳng với hệ trục tọa độ Oxy. Trong các phương trình sau, phương trình nào là phương trình đường tròn? Câu 12: Có 6 người đến nghe buổi hòa nhạc. Số cách sắp xếp 6 người này vào một hàng ngang 6 ghế là? Câu 10: Lớp 10A1 có 20 bạn Nam và 15 bạn nữ. Hỏi giáo viên chủ nhiệm lớp có bao nhiêu cách cử một học sinh trong lớp đi dự đại hội? Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đón xem.

Chủ đề:

Đề HK1 Toán 11 466 tài liệu

Môn:

Toán 11 3.2 K tài liệu

Thông tin:
17 trang 1 tuần trước
Tác giả:
Student
0136_Trần Thảo Vy
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Đề thi học kỳ 1 môn Toán lớp 11 năm học 2024 - 2025 - Đề số 1 | Bộ sách Kết nối tri thức

Câu 1:  Chọn mệnh đề đúng trong các mệnh đề sau?  Câu 7: Trong mặt phẳng với hệ trục tọa độ Oxy. Trong các phương trình sau, phương trình nào là phương trình đường tròn? Câu 12: Có 6 người đến nghe buổi hòa nhạc. Số cách sắp xếp 6 người này vào một hàng ngang 6 ghế là? Câu 10: Lớp 10A1 có 20 bạn Nam và 15 bạn nữ. Hỏi giáo viên chủ nhiệm lớp có bao nhiêu cách cử một học sinh trong lớp đi dự đại hội? Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đón xem.

34 17 lượt tải Tải xuống

Chủ đề: Đề HK1 Toán 11 466 tài liệu

Môn: Toán 11 3.2 K tài liệu

Sách: Kết nối tri thức

Thông tin:

17 trang 1 tuần trước

Tác giả:

Profile 0136_Trần Thảo Vy
Trang 1


(Đề có 05 trang)
- 2024
MÔN: TOÁN - 
Thời gian làm bài: 90 phút (không kể thời gian phát đề)
1
Họ và tên thí sinh: ................................................................ Số báo danh: ...................................
I.  (7,0 điểm).
Câu 1: Chn m  sau:
A.
cos sin
2





. B.
sin sin

.
C.
cos sin
2





. D.
tan 2 cot 2

.
Câu 2: Cho góc
tha mãn
12
sin
13
và
2


. Tính
.
A.
1
cos
13
. B.
5
cos
13
. C.
5
cos
13

. D.
1
cos
13

.
Câu 3: Công thsai?
A.
cos cos cos sin sina b a b a b
. B.
cos cos cos sin sina b a b a b
.
C.
sin sin cos cos sina b a b a b
. D.
sin sin cos cos sina b a b a b
.
Câu 4: Tnh ca hàm s
tan
3
yx




là:
A.
D\
6
kk



. B.
D\
6
kk



.
C.
D\
3
kk



. D.
D\
2
kk



.
Câu 5: Hàm s hàm s l?
A.
1 os f x c x
. B.
2
sinf x x
. C.
cos2f x x
. D.
tanf x x x
.
Câu 6: Nghim c
1
cos2
2
x
là
A.
6
xk
. B.
2
6
xk
. C.
3
xk
. D.
2
3
xk
.
Câu 7: Cho dãy s
n
u
, bit
.
1
n
n
u
n
 hu tiên ca dãy s t là nhng s nào

Trang 2
A.
1 2 3 4 5
, ; ; ; .
2 3 4 5 6

B.
2 3 4 5 6
; ; ; ; .
3 4 5 6 7
C.
1 2 3 4 5
, ; ; ; .
2 3 4 5 6
D.
2 3 4 5 6
; ; ; ; .
3 4 5 6 7
Câu 8: Trong các dãy s
n
u
 nào là dãy s b chn?
A.
2
1
n
un
. B.
1
n
un
n

. C.
21
n
n
u 
. D.
1
n
n
u
n
Câu 9: Cho dãy s
n
u
nh bi
12
12
1; 1
2 3;
n n n
uu
u u u n n


. Giá tr
45
uu
là:
A. 16. B. 20. C. 22. D. 24.
Câu 10: Trong các dãy s sau, dãy s nào là mt cp s cng ?
A.
1; 3; 7; 11; 15;...
. B.
1; 3; 6; 9; 12;...
. C.
1; 2; 4; 6; 8 ;...
. D.
1; 3; 5; 7; 9;...
.
Câu 11: 
n
u

1
7u
và
2
4u

A.
3
. B.
5
2
. C.
2
5
. D. 3.
Câu 12: 
n
u

1
3u
và công sai
2d


A.
21
n
un
. B.
3
n
un
. C.
2( 1)
n
un
. D.
2( 1)
n
un
.
Câu 13: 
n
u

q
?
A.
1
,1
nn
uu nq

. B.
1
,1
n
n
u u q n 
.
C.
1
,1
nn
u nuq

. D.
1
1
1
,1
n
n
u u q n
 
Câu 14: 
n
u

q
?
A.
1
1
,2
n
n
nu u q

. B.
1
,2
n
n
u nuq
.
C.
1
,2
n
n
u u q n 
. D.
1
1
,2
n
n
u nuq

Câu 15: 
2
lim
n




A. 1. B. 2. C. 0. D. 3.
Câu 16: 
lim 1
n
u

lim 2 3
n
u

A.
1
. B. 1. C.

. D. 3.
Câu 17: 
n
u

lim 4 3
n
u

lim
n
u

A.
1
. B. 1. C.
7
. D. 3.
Câu 18: 
2
lim
2
n
n

A.
1
2
. B.

. C.
1
. D.
2
.
Trang 3
Câu 19: 
1
lim 1
x
x

A.
0
. B. 1. C.
1
. D. 2.
Câu 20: 

0
lim 3
x
fx

0
lim2
x
fx

A.
6
. B.
2
. C.
3
. D.
5
.
Câu 21: 
2
15
lim
2
x
x
x

A.
0
. B.
1
. C.

. D.

.
Câu 22: Tính
3
27
lim
3
x
x
x
.
A.

. B.

. C.
0
. D.
2
.
Câu 23: Cho gii hn
22
2
lim 2 3 3
x
x ax a

thì
a
bng bao nhiêu?
A.
2a
. B.
0a
C.
2a 
. D.
1a 
.
Câu 24: Hàm s c ti
2x
?
A.
2
2 6 1
()
2
xx
fx
x

. B.
1
()
2
x
fx
x
. C.
2
1
()
2
xx
fx
x

. D.
2
2
32
()
4
xx
fx
x

.
Câu 25: Tính
2
3
26
lim
3
x
x
ab
x

22
ab
bng
A.
6
. B.
7
. C.
10
. D.
25
.
Câu 26: Tìm giá tr ca tham s
m
sao cho hàm s
3 1 1
1
x khi x
fx
m khi x

liên tc ti
1
o
x 
A.
2m 
. B.
2m
. C.
3m
. D.
0m
.
Câu 27: Tui th 
Giá tr i din ca nhóm
2,5;3
là
A.
2,9
. B.
2,7
. C.
2,8
. D.
2,75
.
Câu 28: Tui th 
C mu ca mu s liu ghép nhóm trên là
A.
50
. B.
48
. C.
14
. D.
6
.
Câu 29: Tìm cân nng trung bình ca hc sinh lp 11B3 cho trong bi
Trang 4
A.
56,71
. B.
52,81
. C.
53,15
. D.
.
Câu 30: Cho hình chóp
.S ABCD
. Giao tyn ca hai mt phng
SAC
và
SBD
là
A. ng th
S
m cng thng
,AB
CD
.
B. ng th
S
m cng thng
,AD
BC
.
C. ng th
S
m cng thng
,AC
BC
.
D. ng th
S
m cng thng
,AC
BD
.
Câu 31: Cho t din
ABCD
. Trên các cnh
AB
và
AC
lm
M
và
N
sao cho
AM BM
và
2AN NC
. Giao tuyn ca mt phng
DMN
và mt phng
ACD
ng thng nào

A.
DN
. B.
MN
. C.
DM
. D.
AC
.
Câu 32: Cho hình chóp
.S ABCD

ABCD
là hình bình hành. Gi
là giao tuyn chung ca hai
mt phng
SAD
và
SBC
ng thng
song song vng th
A. ng thng
AB
. B. ng thng
AD
.
C. ng thng
AC
. D. ng thng
SA
.
Câu 33: Cho t din
ABCD
. Gm
,MN
lm ca các cnh
,AB AC
ng
thng
MN
song song vi mt ph
A. Mt phng
ABD
. B. Mt phng
ACD
.
C. Mt phng
ABC
. D. Mt phng
BCD
.
Câu 34: Cho hình hp
.ABCD A B C D
có
AC
ct
BD
ti
O
còn
AC

ct
BD

ti
O
  
AB D

song song vi mt ph
A.
A OC

. B.
BDA
. C.
BDC
. D.
BCD
.
Câu 35: Xét mt phép chiu song song bt kì. Trong các m sau, m nào sai?
A. Hình chiu song song cng thng chéo nhau có th song song vi nhau.
B. Mng thng có th trùng vi hình chiu ca nó.
C. Hình chiu song song cng thng chéo nhau có th trùng nhau.
D. Mt tam giác bt k u có th xem là hình biu din ca mt tam giác cân.
II.  (3,0 điểm).
Câu 36: Gi
sin4 cos5 0xx
.
Câu 37: Cho hàm s
2
32
khi 1
1
3 khi 1
x
x
fx
x
mx

. Tìm
m
 hàm s liên tc ti
0
1x
.
Câu 38:
Trang 5
Mi mun mua mt thanh g   ct ra làm các thanh ngang ca mt cái thang. Bit
rng chiu dài các thanh ngang c bi cùng) lt là
45 cm,43 cm
,
41 cm, ,31 cm
.
c? Tính chiu dài thanh g n mua, gi s chiu dài
các mi ni (phn g b c.
Câu 39:

 

Hình 3
--------------  --------------
Trang 6
M
I.  (7,0 điểm).
B
1.A
2.D
3.B
4.A
5.D
6.A
7.A
8.D
9.A
10.A
11.A
12.A
13.A
14.A
15.C
16.A
17.A
18.A
19.A
20.A
21.D
22.A
23.C
24.A
25.D
26.A
27.D
28.A
29.D
30.D
31.A
32.B
33.D
34.C
35.C
T
Câu 1: Chn m  sau
A.
cos sin
2





. B.
sin sin

.
C.
cos sin
2





. D.
tan 2 cot 2

.
Li gii
Chn A
Câu 2: Cho góc
tha mãn
12
sin
13
và
2


. Tính
.
A.
1
cos
13
. B.
5
cos
13
. C.
5
cos
13

. D.
1
cos
13

.
Li gii
Chn D
Ta có : Vì
2


nên
cos 0
.
2
2 2 2 2
12 25
sin os 1 os 1 sin 1
13 169
cc



5
cos
13
.
Câu 3: Công thsai?
A.
cos cos cos sin sina b a b a b
. B.
cos cos cos sin sina b a b a b
.
C.
sin sin cos cos sina b a b a b
. D.
sin sin cos cos sina b a b a b
.
Li gii
Chn B
Ta có
cos cos cos sin sina b a b a b
Câu 4: Tnh ca hàm s
tan
3
yx




là:
A.
D\
6
kk



. B.
D\
6
kk



.
Trang 7
C.
D\
3
kk



. D.
D\
2
kk



.
Li gii
Chn A
Hàm s
tan
3
yx




nh khi:
cos 0
3 3 2 6
x x k x k




.
Câu 5: Hàm s hàm s l?
A.
1 os f x c x
. B.
2
sinf x x
. C.
cos2f x x
. D.
tanf x x x
.
Li gii
Chn D
Hàm s
tanf x x x
có tnh
\,
2
D k k



nên
x D x D
Ta có
tan tan , .f x x x x x f x x D
Nên hàm s
tanf x x x
là hàm s l.
Câu 6: Nghim c
1
cos2
2
x
là
A.
6
xk
. B.
2
6
xk
. C.
3
xk
. D.
2
3
xk
.
Li gii
Chn A
1
cos2 2 2
2 3 6
x x k x k k


.
Câu 7: Cho dãy s
n
u
, bit
.
1
n
n
u
n
 hu tiên ca dãy s t là nhng s nào

A.
1 2 3 4 5
, ; ; ; .
2 3 4 5 6

B.
2 3 4 5 6
; ; ; ; .
3 4 5 6 7
C.
1 2 3 4 5
, ; ; ; .
2 3 4 5 6
D.
2 3 4 5 6
; ; ; ; .
3 4 5 6 7
Li gii
Chn A
Ta có
1 2 3 4 5
1 2 3 4 5
; ; ; ;
2 3 4 5 6
u u u u u
.
Câu 8: Trong các dãy s
n
u
 nào là dãy s b chn?
A.
2
1
n
un
. B.
1
n
un
n

. C.
21
n
n
u 
. D.
1
n
n
u
n
Li gii
Trang 8
Chn D
Các dãy s
2
; ;2
n
nn

n
n, nên các
dãy
2
1n
;
;
21
n

ch chn.
Nhn xét:
1
0 1 1
11
n
n
u
nn

.
Câu 9: Cho dãy s
n
u
nh bi
12
12
1; 1
2 3;
n n n
uu
u u u n n


. Giá tr
45
uu
là:
A. 16. B. 20. C. 22. D. 24.
Li gii
Chn A
Ta có
3 2 1
4 3 2
5 4 3
2 1 2.1 3.
2 3 2.1 5.
2 5 2.3 11.
u u u
u u u
u u u
Vy
45
5 11 16.uu
Câu 10: Trong các dãy s sau, dãy s nào là mt cp s cng ?
A.
1; 3; 7; 11; 15;...
. B.
1; 3; 6; 9; 12;...
. C.
1; 2; 4; 6; 8 ;...
. D.
1; 3; 5; 7; 9;...
.
Li gii
Chn A
Ta lt kim tra :
2 1 3 2 4 3
...?u u u u u u

2 1 3 2 4 3
1; 3; 7; 11; 15;... ...u u u u u u
chn

2 1 3 2
1; 3; 6; ; 1;... 4 3u u u u
loi

2 1 3 2
1; 2; 4; 6; 8;... 3 2u u u u
loi

2 1 3 2
1; 3; 5; ;7 9;... 4 2u u u u
loi
Câu 11: 
n
u

1
7u
và
2
4u
 
A.
3
. B.
5
2
. C.
2
5
. D. 3.
Li gii
Chn A
Công sai ca cp s cng:
21
4 7 3d u u
.
Câu 12: 
n
u

1
3u
và công sai
2d


A.
21
n
un
. B.
3
n
un
. C.
2( 1)
n
un
. D.
2( 1)
n
un
.
Li gii
Chn A
Trang 9
S hng tng quát ca cp s cng:
1
( 1).23 2 1
n
nu u d n 
Câu 13: 
n
u

q
?
A.
1
,1
nn
uu nq

. B.
1
,1
n
n
u u q n 
.
C.
1
,1
nn
u nuq

. D.
1
1
1
,1
n
n
u u q n
 
Li gii
Chn A
 hng tng quát ca cp s nhân:
1
,1
nn
uu nq

.
Câu 14: 
n
u

q
?
A.
1
1
,2
n
n
nu u q

. B.
1
,2
n
n
u nuq
.
C.
1
,2
n
n
u u q n 
. D.
1
1
,2
n
n
u nuq

Li gii
Chn A
p s nhân, ta có
1
1
,2
n
n
nu u q

Câu 15: 
2
lim
n




A. 1. B. 2. C. 0. D. 3.
Li gii
Chn C
Ta có, theo h qu
1
lim 0 lim 0,
k
k
nn
Câu 16: 
lim 1
n
u

lim 2 3
n
u

A.
1
. B. 1. C.

. D. 3.
Li gii
Chn A
         
lim 2 3 lim2 lim3 2.lim 3 2.1 3 1
n n n
u u u
Câu 17: 
n
u

lim 4 3
n
u

lim
n
u

A.
1
. B. 1. C.
7
. D. 3.
Li gii
Chn A
lim 4 3 lim4 lim 3 4 lim 3 lim 1
n n n n
u u u u
Câu 18: 
2
lim
2
n
n

A.
1
2
. B.

. C.
1
. D.
2
.
Li gii
Trang 10
Chn A
2
1
21
lim lim
2 2 2
n
n
n

Câu 19: 
1
lim 1
x
x

A.
0
. B. 1. C.
1
. D. 2.
Li gii
Chn A
Vì
1
lim 1 1 1 0
x
x
Câu 20: 

0
lim 3
x
fx

0
lim2
x
fx

A.
6
. B.
2
. C.
3
. D.
5
.
Li gii
Chn A
00
lim2 2.lim 2.3 6
xx
f x f x

Câu 21: 
2
15
lim
2
x
x
x

A.
0
. B.
1
. C.

. D.

.

Chn D

2
2
lim 15 13 0
lim 2 0
x
x
x
x

.

2x
nên
2x

20x
.

2
15
lim
2
x
x
x

.
Câu 22: Tính
3
27
lim
3
x
x
x
.
A.

. B.

. C.
0
. D.
2
.
Li gii
Chn A
Ta có:
3
lim 2 7 13 0
x
x
,
3
lim 3 0
x
x

,
3 3 0xx
.
Vy,
3
27
lim
3
x
x
x

.
Câu 23: Cho gii hn
22
2
lim 2 3 3
x
x ax a

thì
a
bng bao nhiêu?
A.
2a
. B.
0a
C.
2a 
. D.
1a 
.
Trang 11
Li gii
Chn C
Ta có,
2
2 2 2 2
2
lim 2 3 2 2 ( 2) 3 4 7
x
x ax a a a a a

.
22
2
lim 2 3 3
x
x ax a

.
2
4 7 3aa
.
2
4 4 0aa
.
2a
.
Câu 24: Hàm s c ti
2x
?
A.
2
2 6 1
()
2
xx
fx
x

. B.
1
()
2
x
fx
x
. C.
2
1
()
2
xx
fx
x

. D.
2
2
32
()
4
xx
fx
x

.
Li gii
Chn A
Hàm s
2
2 6 1
()
2
xx
fx
x

là hàm phân thc hu t nh ti
2x
nên nó liên tc ti
2x
.
Câu 25: Tính
2
3
26
lim
3
x
x
ab
x

22
ab
bng
A.
6
. B.
7
. C.
10
. D.
25
.
Li gii
Chn D
2
2
3 3 3 3
2 3 3
23
26
lim lim lim lim 2 3 4 3
3 3 3
x x x x
xx
x
x
x
x x x

.
Suy ra
22
4, 3 25a b a b
.
Câu 26: Tìm giá tr ca tham s
m
sao cho hàm s
3 1 1
1
x khi x
fx
m khi x

liên tc ti
1
o
x 
A.
2m 
. B.
2m
. C.
3m
. D.
0m
.
Li gii
Chn A
Tnh ca hàm s
fx
là
D
. Ta có:
1fm
.
11
lim lim 3 1 3. 1 1 2
xx
f x x
 
.
Hàm s c ti
1
o
x 
khi
1
1 lim 2
x
f f x m

.
Trang 12
Vy
2m 
tha yêu cu bài toán.
Câu 27: Tui th 
Giá tr i din ca nhóm
2,5;3
là
A.
2,9
. B.
2,7
. C.
2,8
. D.
2,75
.
Li gii
Chn D
Giá tr i din ca nhóm
2,5;3
là:
2,5 3
2,75
2
.
Câu 28: Tui th 
C mu ca mu s liu ghép nhóm trên là
A.
50
. B.
48
. C.
14
. D.
6
.
Li gii
Chn A
C mu ca mu s liu ghép nhóm trên là:
4 9 14 11 7 5 50n
Câu 29: Tìm cân nng trung bình ca hc sinh lp 11B3 cho trong bi
A.
56,71
. B.
52,81
. C.
53,15
. D.
.
Li gii
Chn D
Trong mi khong cân nng, giá tr i din là trung bình cng ca giá tr u mút nên ta có
bng sau
Tng s hc sinh là
42n
. Cân nng trung bình ca hc sinh lp 11B3 là
(kg)
10.43 7.48 16.53 4.58 2.63 3.68
51,81
42
x

Câu 30: Cho hình chóp
.S ABCD
. Giao tyn ca hai mt phng
SAC
và
SBD
là
A. ng th
S
m cng thng
,AB
CD
.
Trang 13
B. ng th
S
m cng thng
,AD
BC
.
C. ng th
S
m cng thng
,AC
BC
.
D. ng th
S
m cng thng
,AC
BD
.
Li gii
Chn D
Ta có:
S SAC SBD
.
Trong
ABCD
, gi
O AC BD
thì
O AC SAC O SAC
O BD SBD O SBD
.
Vy
SO SAC SBD
.
Câu 31: Cho t din
ABCD
. Trên các cnh
AB
và
AC
lm
M
và
N
sao cho
AM BM
và
2AN NC
. Giao tuyn ca mt phng
DMN
và mt phng
ACD
ng thng nào

A.
DN
. B.
MN
. C.
DM
. D.
AC
.
Li gii
Chn A
Giao tuyn ca mt phng
DMN
và mt phng
ACD
ng thng
DN
.
Câu 32: Cho hình chóp
.S ABCD

ABCD
là hình bình hành. Gi
là giao tuyn chung ca hai
mt phng
SAD
và
SBC
ng thng
song song vng th
A. ng thng
AB
. B. ng thng
AD
.
M
B
C
D
A
N
Trang 14
C. ng thng
AC
. D. ng thng
SA
.
Li gii
Chn B
Hai mt phng
SAD
và
SBC
m
S
và lt chng thng song
song
AD
,
BC
nên giao tuyn

S
và lt song song vi
AD
,
BC
.
Câu 33: Cho t din
ABCD
. Gm
,MN
lm ca các cnh
,AB AC
ng
thng
MN
song song vi mt ph
A. Mt phng
ABD
. B. Mt phng
ACD
.
C. Mt phng
ABC
. D. Mt phng
BCD
.
Li gii
Chn D
Vì
MN
 ng trung bình ca tam giác
ABC
nên
//MN BC
mà
BC BCD
nên
//MN BCD
.
Câu 34: Cho hình hp
.ABCD A B C D
có
AC
ct
BD
ti
O
còn
AC

ct
BD

ti
O

AB D

song song vi mt ph
A.
A OC

. B.
BDA
. C.
BDC
. D.
BCD
.
Li gii
A
D
B
C
S
N
M
B
C
D
A
Trang 15
Chn C
Vì
//B D BD
nên
//B D BDC
. Vì
//AD BC
nên
//AD BDC
.
T 
//AB D BDC
.
Câu 35: Xét mt phép chiu song song bt kì. Trong các m sau, m nào sai?
A. Hình chiu song song cng thng chéo nhau có th song song vi nhau.
B. Mng thng có th trùng vi hình chiu ca nó.
C. Hình chiu song song cng thng chéo nhau có th trùng nhau.
D. Mt tam giác bt k u có th xem là hình biu din ca mt tam giác cân.
Li gii
Chn C
Xét hình hp
.ABCD A B C D
và phép chiu lên mt phng
A B C D
u
AA
.
ng thng
AD
,
BC
chéo nhau và có hình ching thng
AD
,
BC
song
song.
* Mng thng nm trên mt phng chiu có hình chiu là chính nó.
ng thng chéo nhau
,ab
. Gi
P
là mt phng cha
a
, hình chiu ca
a
trên
mt phng chiu
Q
là
a
. Vì
b
không thuc
P
nên hình chiu ca
b
không trùng
a
.
* Khi
A B A D
thì mi tam giác
MB D
(
M AA
u có hình biu din là tam giác cân
A B D
.
O'
O
A
B
D
C
C'
D'
B'
A'
A
B
D
C
C'
D'
B'
A'
M
Trang 16
II.  (3,0 điểm).
Câu


36
Gi
sin4 cos5 0xx
.
0.5
Ta có
sin4 cos5 0xx
cos5 cos 4
2
xx



0.25
5 4 2
2
5 4 2
2
x x k
x x k
2
2
2
18 9
xk
k
xk



.
0.25
37
Cho hàm s
2
32
khi 1
1
3 khi 1
x
x
fx
x
mx

. Tìm
m
 hàm s liên tc ti
0
1x
.
0.5
Hàm s nh ti
0
1x
,
13fm
.
1
lim
x
fx
2
1
2
1
lim
1 3 2
x
x
xx
1
2
11
lim
1 3 2
x
xx
xx

2
1
11
lim
2
32
x
x
x


.
0.25
Hàm s    c ti
0
1x
1
lim 1
x
f x f
1
3
2
m
5
2
m
.
Vy
5
2
m
.
0.25
38
M i mun mua mt thanh g   ct ra làm các thanh
ngang ca mt cái thang. Bit rng chiu dài các thanh ngang ca
    b i cùng) l t là
45 cm,43 cm
,
41 cm, ,31 cm
.
c? Tính chiu dài thanh g n
0.5
Trang 17
mua, gi s chiu dài các mi ni (phn g b c
.
Chiu dài các thanh ngang ca cái thang (tính t bi cùng) to thành
mt cp s cng có:
1
45; 2ud
.
Suy ra
45 31
18
2
n
.
c.
0,25
Ta li có
8
8 45 31
304
2
S

.
Vn mua thanh g có chiu dài 304 cm.
0,25
39


               
trên?
0.5
Ta có dãy s:
1;1;2;3;5;8;1 3;21
.
0,25
Nhn xét: K t s hng th ba, mi s hng ca dãy bng tng ca hai s
hng lic.
0,25
--------------  --------------
| 1/17

Tài liệu khác của Toán 11

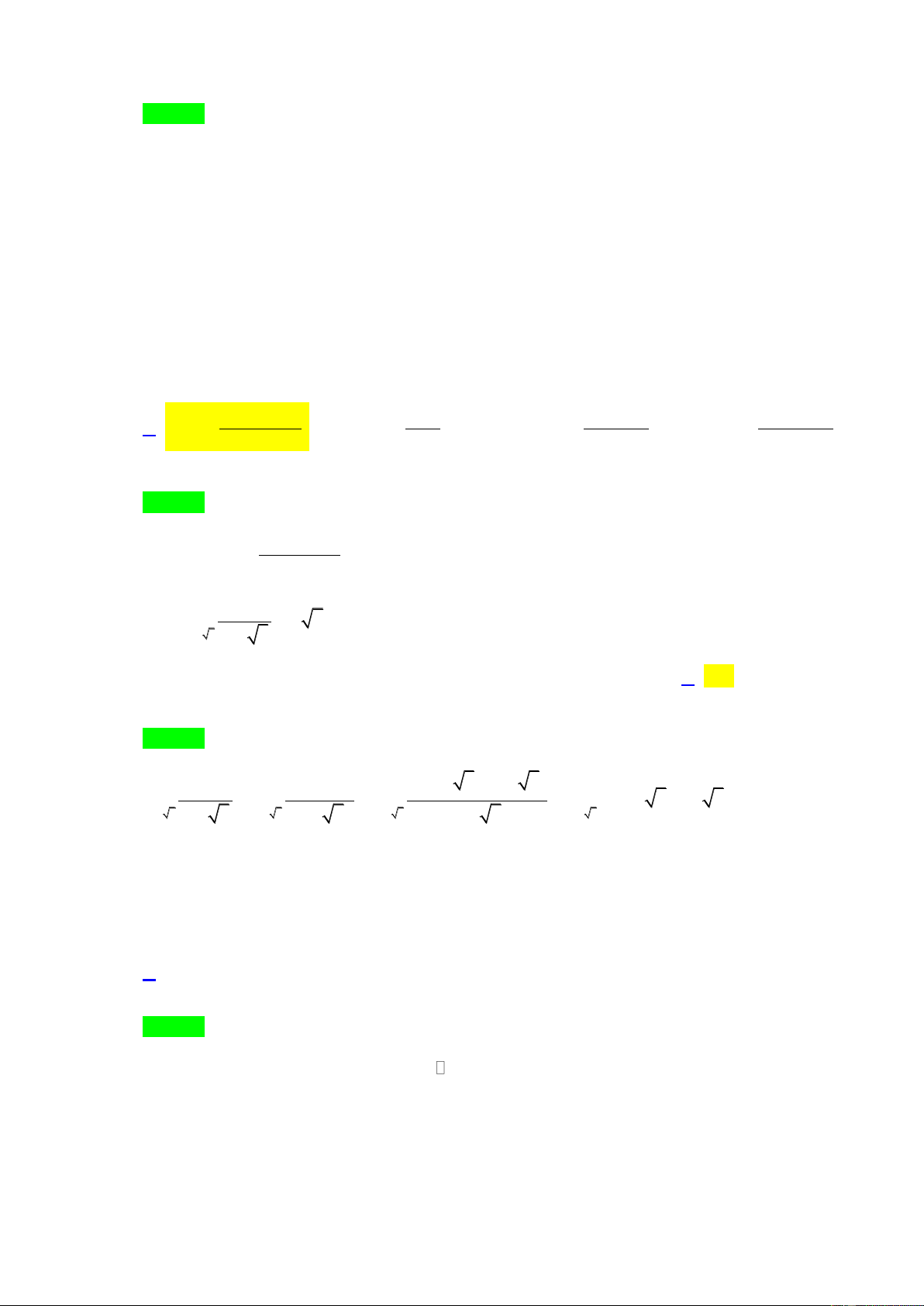
Preview text:

TRƯỜNG THPT
ĐỀ KIỂM TRA CUỐI KÌ I NĂM HỌC 2023 - 2024 ĐỀ CHÍNH THỨC
MÔN: TOÁN - LỚP: 11 (SÁCH KNTT) (Đề có 05 trang)
Thời gian làm bài: 90 phút (không kể thời gian phát đề) ĐỀ 1
Họ và tên thí sinh: ................................................................ Số báo danh: ...................................
I. PHẦN TRẮC NGHIỆM (7,0 điểm). Câu 1:
Chọn mệnh đề đúng trong các mệnh đề sau:    A. cos   sin   .
B. sin     sin .  2     C. cos   sin   .
D. tan   2   cot 2 .  2  12  Câu 2:
Cho góc  thỏa mãn sin   và
    . Tính cos . 13 2 1 5 5 1 A. cos  . B. cos  . C. cos   . D. cos   . 13 13 13 13 Câu 3:
Công thức nào sau đây sai?
A. cos a b  cos a cosb  sin a sin b .
B. cos a b  cos a cosb  sin a sin b .
C. sin a b  sin a cosb  cos a sin b .
D. sin a b  sin a cosb  cos a sin b .    Câu 4:
Tập xác định của hàm số y  tan x    là:  3       A. D 
\   kk   . B. D  \ 
kk  .  6   6      C. D 
\   kk   . D. D 
\   kk   .  3   2  Câu 5:
Hàm số nào sau đây là hàm số lẻ?
A. f x  1 o c s x .
B. f x 2  sin x .
C. f x  cos 2x .
D. f x  x  tan x . Câu 6:
Nghiệm của phương trình 1 cos 2x  là 2     A. x    k . B. x    k2 . C. x    k . D. x    k2 . 6 6 3 3 n Câu 7:
Cho dãy số u , biết u  . n n n
Năm số hạng đầu tiên của dãy số đó lần lượt là những số nào 1 dưới đây? Trang 1 1 2 3 4 5 2 3 4 5 6
A.  ,  ;  ;  ;  .
B.  ;  ;  ;  ;  . 2 3 4 5 6 3 4 5 6 7 1 2 3 4 5 2 3 4 5 6 C. , ; ; ; . D. ; ; ; ; . 2 3 4 5 6 3 4 5 6 7 Câu 8:
Trong các dãy số u sau đây, dãy số nào là dãy số bị chặn? n  1 n A. 2 u n 1 .
B. u n  .
C. u  2n 1. D. u n n n n n n  1 u  1; u 1  1 2 Câu 9:
Cho dãy số u xác định bởi 
. Giá trị u u là: n u
  u  2u n  3;n  4 5 n n 1  n2   A. 16. B. 20. C. 22. D. 24.
Câu 10: Trong các dãy số sau, dãy số nào là một cấp số cộng ? A. 1; 3  ; 7  ; 11  ; 15  ;... . B. 1; 3  ; 6  ; 9  ; 12
 ;... . C. 1;2;4;6;8 ;
 ... . D. 1;3;5;7;9;... .
Câu 11: Cho cấp số cộng u với u  7 và u  4 . Công sai của cấp số cộng đã cho bằng n  1 2 5 2 A. 3  . B. . C. . D. 3. 2 5
Câu 12: Cho cấp số cộng u vói số hạng đầu u  3 và công sai d  2 . Số hạng tổng quát của cấp số n  1
cộng đã cho được tính theo công thức nào dưới đây?
A. u  2n 1.
B. u  3  n .
C. u  2(n 1) .
D. u  2(n 1) . n n n n
Câu 13: Cho cấp số nhân u có công bội q . Mệnh đề nào sau đây đúng? n A. u
u q, n  1. B. n
u u q , n  1. n 1  n n 1 
C. u uq, n  1. D. n 1 u
u q , n  1 n n 1  n 1  1
Câu 14: Cho cấp số nhân u có công bội q . Mệnh đề nào sau đây đúng? n A. n 1 u u q   , n   2. B. n u u  , q n   2. n 1 n 1  C. n
u u q , n   2 . D. n 1 u u  , q n   2 n 1 n 1  
Câu 15: Giá trị của 2 lim  bằng  n A. 1. B. 2. C. 0. D. 3.
Câu 16: Cho biết lim u   1. Giá trị của lim2u  3 bằng nn A. 1. B. 1. C.  . D. 3.
Câu 17: Cho dãy số u thỏa mãn lim4  u  . Giá trị của limu bằng n n  3 n A. 1. B. 1. C. 7 . D. 3. n
Câu 18: Giá trị của 2 lim bằng 2n 1 A. . B.  . C. 1. D. 2 . 2 Trang 2
Câu 19: Giá trị của lim  x   1 bằng x 1  A. 0 . B. 1. C. 1. D. 2.
Câu 20: Cho hàm số f x thỏa mãn lim f x  3 . Giá trị của lim 2 f x bằng x0 x0 A. 6 . B. 2 . C. 3 . D. 5 . x 15
Câu 21: ết qu của giới hạn lim là x2 x  2 A. 0 . B. 1. C.  . D.  . 2x  7 Câu 22: Tính lim x3 x  . 3 A.  . B.  . C. 0 . D. 2 .
Câu 23: Cho giới hạn lim  2 2
x  2ax  3  a   3 thì a bằng bao nhiêu? x 2 
A. a  2 .
B. a  0 C. a  2  . D. a  1  .
Câu 24: Hàm số nào sau đây liên tục tại x  2 ? 2 2x  6x 1 x 1 2 x x 1 2 3x x  2
A. f (x) 
. B. f (x)  .
C. f (x)  .
D. f (x)  . x  2 x  2 x  2 2 x  4 2 2x  6 Câu 25: Tính lim  a b . hi đó 2 2
a b bằng x 3 x  3 A. 6 . B. 7 . C. 10 . D. 25 .  x khi x  
Câu 26: Tìm giá trị của tham số m sao cho hàm số f x 3 1 1  
liên tục tại x  1  m khi x  1  o A. m  2  . B. m  2 . C. m  3 . D. m  0 .
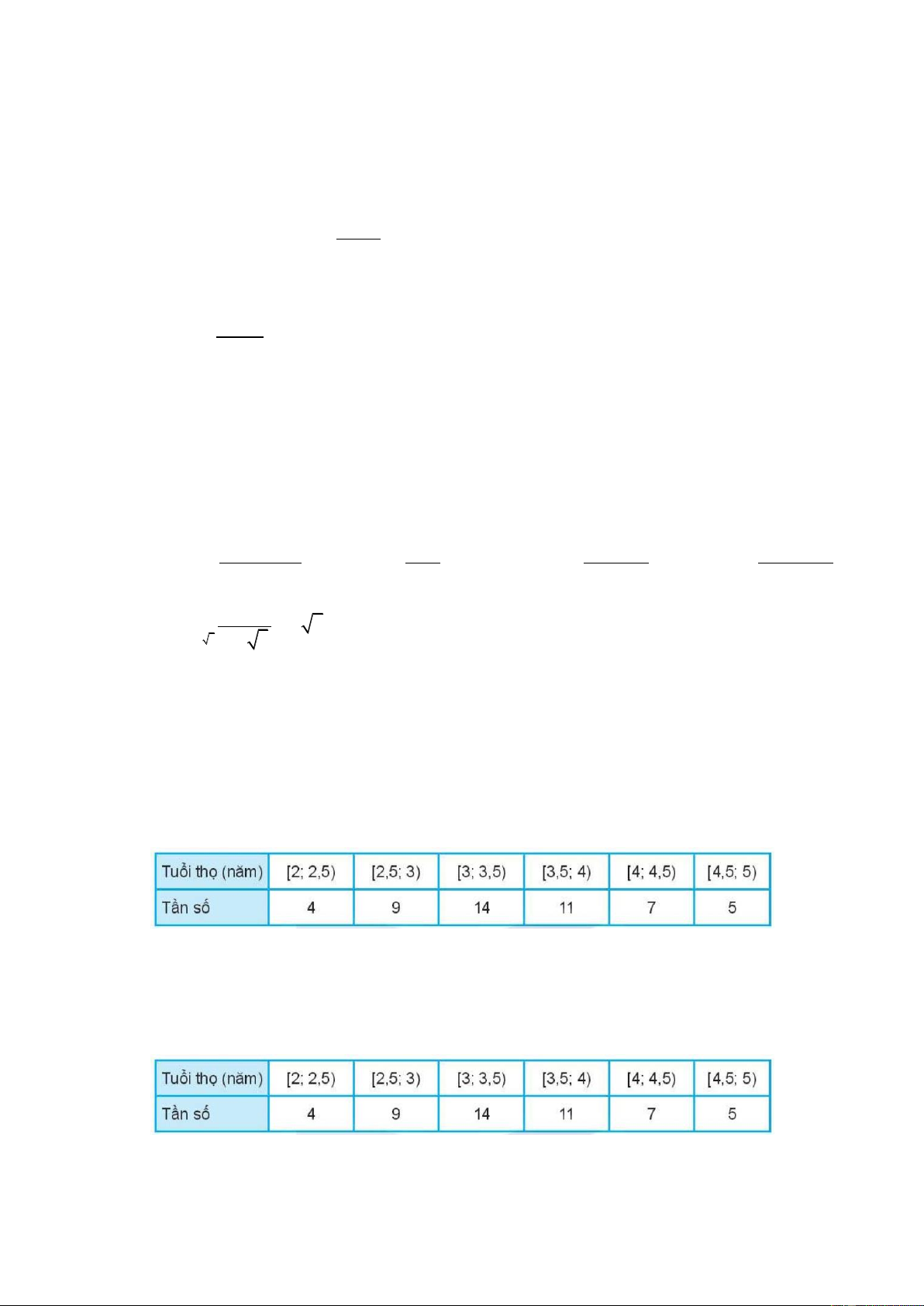
Câu 27: Tuổi thọ (năm) của 50 bình ác quy ô tô được cho như sau
Giá trị đại diện của nhóm 2,5;3 là A. 2, 9 . B. 2, 7 . C. 2, 8 . D. 2, 75 .
Câu 28: Tuổi thọ (năm) của 50 bình ác quy ô tô được cho như sau
Cỡ mẫu của mẫu số liệu ghép nhóm trên là A. 50 . B. 48 . C. 14 . D. 6 .
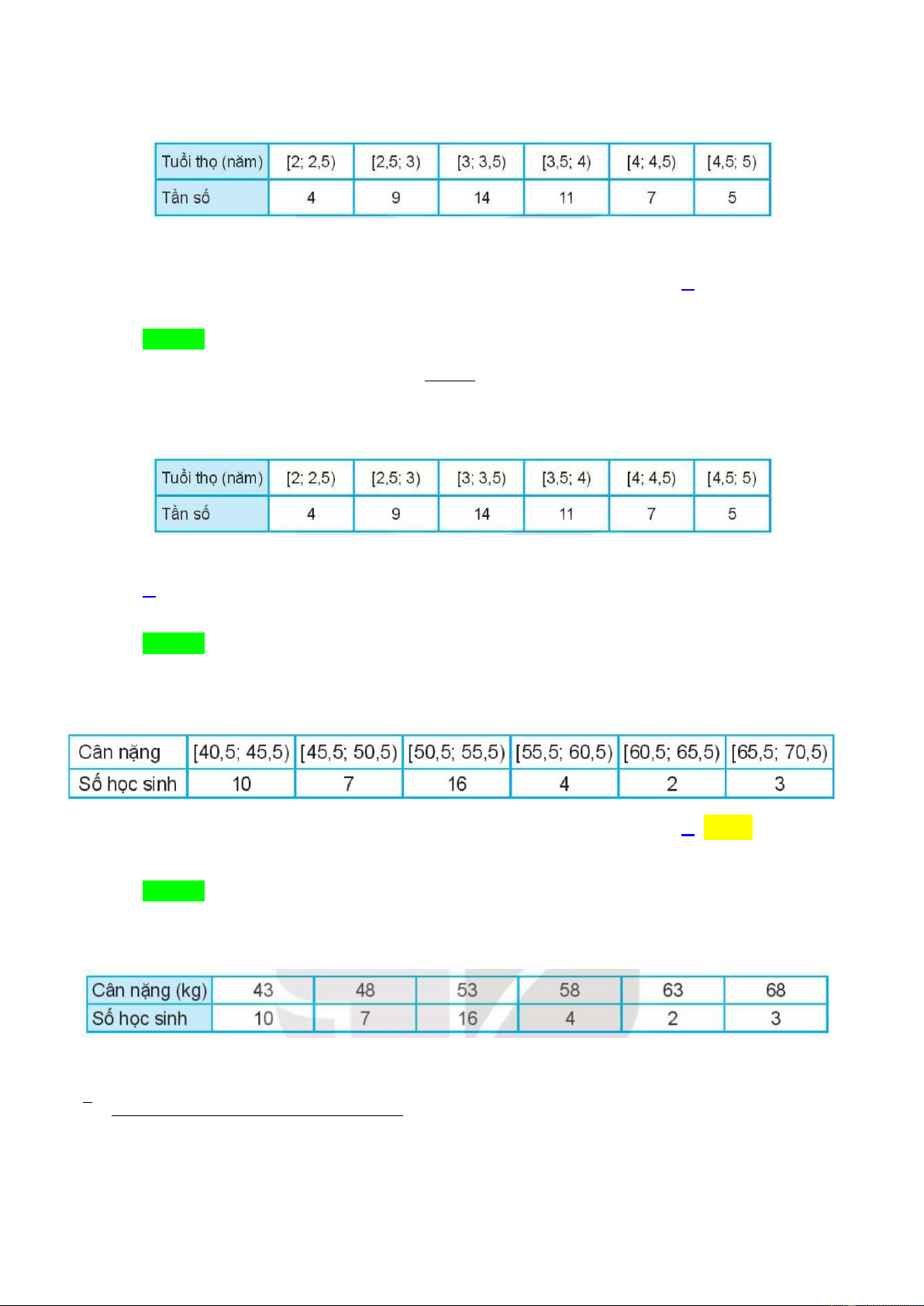
Câu 29: Tìm cân nặng trung bình của học sinh lớp 11B3 cho trong b ng bên dưới Trang 3 A. 56, 71 . B. 52,81. C. 53,15 . D. 51,81.
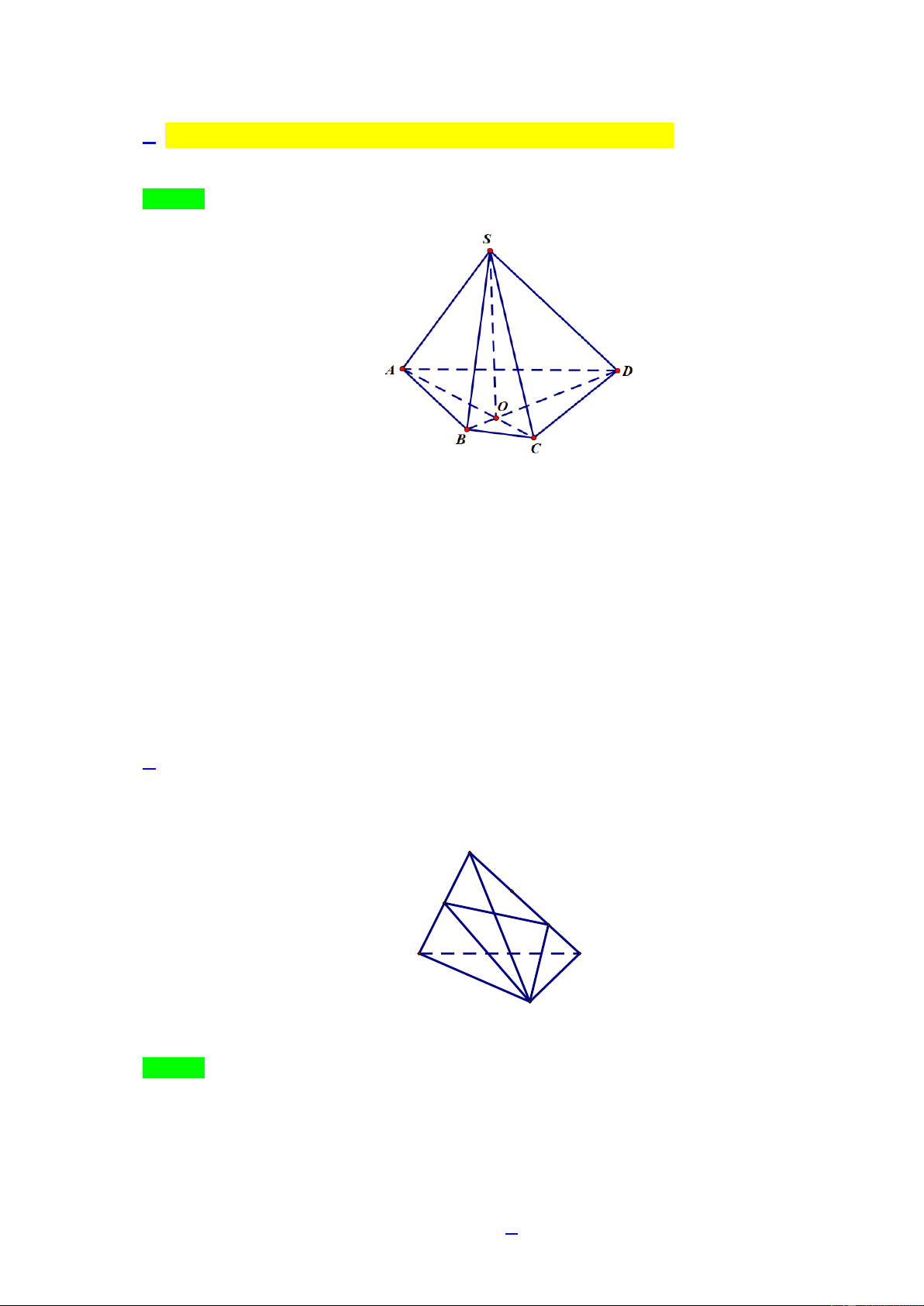
Câu 30: Cho hình chóp S.ABCD . Giao tyến của hai mặt phẳng SAC  và SBD là
A. Đường thẳng đi qua S và giao điểm của hai đường thẳng AB, CD .
B. Đường thẳng đi qua S và giao điểm của hai đường thẳng AD, BC .
C. Đường thẳng đi qua S và giao điểm của hai đường thẳng AC, BC .
D. Đường thẳng đi qua S và giao điểm của hai đường thẳng AC, BD .
Câu 31: Cho tứ diện ABCD . Trên các cạnh AB và AC lấy hai điểm M và N sao cho AM BM và
AN  2NC . Giao tuyến của mặt phẳng  DMN  và mặt phẳng  ACD là đường thẳng nào dưới đây? A. DN . B. MN . C. DM . D. AC .
Câu 32: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi  là giao tuyến chung của hai
mặt phẳng SAD và SBC  . Đường thẳng  song song với đường thẳng nào dưới đây?
A. Đường thẳng AB .
B. Đường thẳng AD .
C. Đường thẳng AC .
D. Đường thẳng SA .
Câu 33: Cho tứ diện ABCD . Gọi hai điểm M , N lần lượt là trung điểm của các cạnh AB, AC . Đường
thẳng MN song song với mặt phẳng nào sau đây?
A. Mặt phẳng  ABD .
B. Mặt phẳng  ACD .
C. Mặt phẳng  ABC  .
D. Mặt phẳng  BCD .
Câu 34: Cho hình hộp ABC . D A BCD
  có AC cắt BD tại O còn A C   cắt B D
  tại O . hi đó AB D
  song song với mặt phẳng nào dưới đây? A. A OC .
B. BDA .
C. BDC . D. BCD .
Câu 35: Xét một phép chiếu song song bất kì. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau.
B. Một đường thẳng có thể trùng với hình chiếu của nó.
C. Hình chiếu song song của hai đường thẳng chéo nhau có thể trùng nhau.
D. Một tam giác bất kỳ đều có thể xem là hình biểu diễn của một tam giác cân.
II. PHẦN TỰ LUẬN (3,0 điểm).
Câu 36: Gi i phương trình sin 4x  cos5x  0 . 2  x 3  2  khi x  1
Câu 37: Cho hàm số f x   x 1
. Tìm m để hàm số liên tục tại x  1. 0 
  m  3 khi x 1 Câu 38: Trang 4
Một người muốn mua một thanh gỗ đủ để cắt ra làm các thanh ngang của một cái thang. Biết
rằng chiều dài các thanh ngang của cái thang đó (từ bậc dưới cùng) lần lượt là 45 cm, 43 cm , 41 cm,, 31 cm .
Cái thang đó có bao nhiêu bậc? Tính chiều dài thanh gỗ mà người đó cần mua, gi sử chiều dài
các mối nối (phần gỗ bị cắt thành mùn cưa) là không đáng kể. Câu 39:
Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như
Hình 3. Tìm dãy số biễu diễn độ dài cạnh của 8 hình vuông đó từ nhỏ đến lớn. Có nhận xét gì về dãy số trên? Hình 3
-------------- HẾT -------------- Trang 5
ĐÁP ÁN VÀ BIỂU ĐIỂM
I. PHẦN TRẮC NGHIỆM (7,0 điểm). BẢNG ĐÁP ÁN 1.A 2.D 3.B 4.A 5.D 6.A 7.A 8.D 9.A 10.A 11.A 12.A 13.A 14.A 15.C 16.A 17.A 18.A 19.A 20.A 21.D 22.A 23.C 24.A 25.D 26.A 27.D 28.A 29.D 30.D 31.A 32.B 33.D 34.C 35.C ĐÁP ÁN CHI TIẾT Câu 1:
Chọn mệnh đề đúng trong các mệnh đề sau    A. cos   sin   .
B. sin     sin .  2     C. cos   sin   .
D. tan   2   cot 2 .  2  Lời giải Chọn A 12  Câu 2:
Cho góc  thỏa mãn sin   và
    . Tính cos . 13 2 1 5 5 1 A. cos  . B. cos  . C. cos   . D. cos   . 13 13 13 13 Lời giải Chọn D  Ta có : Vì     cos 0 2 nên   . 2 12 25 2 2 2 2 sin  o c s  1 o c s  1 sin         1    13  169 5  cos   13 . Câu 3:
Công thức nào sau đây sai?
A. cos a b  cos a cosb  sin a sin b .
B. cos a b  cos a cosb  sin a sin b .
C. sin a b  sin a cosb  cos a sin b .
D. sin a b  sin a cosb  cos a sin b . Lời giải Chọn B
Ta có cos a b  cos a cosb  sin a sin b    Câu 4:
Tập xác định của hàm số y  tan x    là:  3       A. D 
\   kk   . B. D  \ 
kk  .  6   6  Trang 6     C. D 
\   kk   . D. D 
\   kk   .  3   2  Lời giải Chọn A         
Hàm số y  tan x  
 xác định khi: cos x
 0  x    k  x   k   .  3   3  3 2 6 Câu 5:
Hàm số nào sau đây là hàm số lẻ?
A. f x  1 o c s x .
B. f x 2  sin x .
C. f x  cos 2x .
D. f x  x  tan x . Lời giải Chọn D  
Hàm số f x  x  tan x có tập xác định D
\   k , k   nên x
 D  xD  2 
Ta có f x  x  tan x  x  tan x   f x, x   . D
Nên hàm số f x  x  tan x là hàm số lẻ. Câu 6:
Nghiệm của phương trình 1 cos 2x  là 2     A. x    k . B. x    k2 . C. x    k . D. x    k2 . 6 6 3 3 Lời giải Chọn A 1   cos 2x
 2x    k2  x    k k   . 2 3 6 n Câu 7:
Cho dãy số u , biết u  . n n n
Năm số hạng đầu tiên của dãy số đó lần lượt là những số nào 1 dưới đây? 1 2 3 4 5 2 3 4 5 6
A.  ,  ;  ;  ;  .
B.  ;  ;  ;  ;  . 2 3 4 5 6 3 4 5 6 7 1 2 3 4 5 2 3 4 5 6 C. , ; ; ; . D. ; ; ; ; . 2 3 4 5 6 3 4 5 6 7 Lời giải Chọn A 1 2 3 4 5
Ta có u   ;u   ;u   ;u   ;u   . 1 2 3 4 5 2 3 4 5 6 Câu 8:
Trong các dãy số u sau đây, dãy số nào là dãy số bị chặn? n  1 n A. 2 u n 1 .
B. u n  .
C. u  2n 1. D. u n n n n n n  1 Lời giải Trang 7 Chọn D Các dãy số 2; ; 2n n n
dương và tăng lên vô hạn (dương vô cùng) khi n tăng lên vô hạn, nên các 1 dãy 2 n 1 ; n
; 2n 1 cũng tăng lên vô hạn (dương vô cùng), suy ra các dãy này không bị n
chặn trên, do đó chúng không bị chặn. n 1
Nhận xét: 0  u   1  1 n n 1 n  . 1 u  1; u 1  1 2 Câu 9:
Cho dãy số u xác định bởi 
. Giá trị u u là: n u
  u  2u n  3;n  4 5 n n 1  n2   A. 16. B. 20. C. 22. D. 24. Lời giải Chọn A Ta có
u u  2u  1 2.1  3. 3 2 1
u u  2u  3  2.1  5. 4 3 2
u u  2u  5  2.3  11. 5 4 3
Vậy u u  5 11  16. 4 5
Câu 10: Trong các dãy số sau, dãy số nào là một cấp số cộng ? A. 1; 3  ; 7  ; 11  ; 15  ;... . B. 1; 3  ; 6  ; 9  ; 12
 ;... . C. 1;2;4;6;8 ;
 ... . D. 1;3;5;7;9;... . Lời giải Chọn A
Ta lần lượt kiểm tra : u u u u u u  ...? 2 1 3 2 4 3 Xét đáp án 1; 3  ; 7  ; 1  1; 1
 5;...  u u u u u u  ...  chọn 2 1 3 2 4 3 Xét đáp án 1; 3  ; 6  ; ;  1
 ;...  u u  4   3
  u u  loại 2 1 3 2 Xét đáp án 1; 2  ; 4  ; 6  ; 8
 ;...  u u  3   2
  u u  loại 2 1 3 2 Xét đáp án 1; 3  ; 5  ; ;
 7  9;...  u u  4   2
  u u loại 2 1 3 2
Câu 11: Cho cấp số cộng u với u  7 và u  4 . Công sai của cấp số cộng đã cho bằng n  1 2 5 2 A. 3  . B. . C. . D. 3. 2 5 Lời giải Chọn A
Công sai của cấp số cộng: d u u  4  7  3  . 2 1
Câu 12: Cho cấp số cộng u vói số hạng đầu u  3 và công sai d  2 . Số hạng tổng quát của cấp số n  1
cộng đã cho được tính theo công thức nào dưới đây?
A. u  2n 1.
B. u  3  n .
C. u  2(n 1) .
D. u  2(n 1) . n n n n Lời giải Chọn A Trang 8
Số hạng tổng quát của cấp số cộng: u u d  3  (n 1).2  2n 1 n 1
Câu 13: Cho cấp số nhân u có công bội q . Mệnh đề nào sau đây đúng? n A. u
u q, n  1. B. n
u u q , n  1. n 1  n n 1 
C. u uq, n  1. D. n 1 u
u q , n  1 n n 1  n 1  1 Lời giải Chọn A
Theo ĐN, Số hạng tổng quát của cấp số nhân: u
u q, n  1. n 1  n
Câu 14: Cho cấp số nhân u có công bội q . Mệnh đề nào sau đây đúng? n A. n 1 u u q   , n   2. B. n u u  , q n   2. n 1 n 1  C. n
u u q , n   2 . D. n 1 u u  , q n   2 n 1 n 1 Lời giải Chọn A
Theo ĐN cấp số nhân, ta có n 1 u u q   , n   2 n 1  
Câu 15: Giá trị của 2 lim  bằng  n A. 1. B. 2. C. 0. D. 3. Lời giải Chọn C  1   k  Ta có, theo hệ qu lim  0  lim  0, k        n   n
Câu 16: Cho biết lim u   1. Giá trị của lim2u  3 bằng nn A. 1. B. 1. C.  . D. 3. Lời giải Chọn A Theo định lý về giới hạn của dãy, ta có
lim2u  3  lim 2u  lim3  2.limu  3  2.1 3  1  n n n
Câu 17: Cho dãy số u thỏa mãn lim4  u  . Giá trị của limu bằng n n  3 n A. 1. B. 1. C. 7 . D. 3. Lời giải Chọn A
lim4  u   3  lim 4  limu  3  4  limu  3  limu  1  n n n n n  2
Câu 18: Giá trị của lim bằng 2n 1 A. . B.  . C. 1. D. 2 . 2 Lời giải Trang 9 Chọn A 2 1 n  2 1 lim  lim n  2n 2 2
Câu 19: Giá trị của lim  x   1 bằng x 1  A. 0 . B. 1. C. 1. D. 2. Lời giải Chọn A Vì lim  x   1  11  0 x 1 
Câu 20: Cho hàm số f x thỏa mãn lim f x  3 . Giá trị của lim 2 f x bằng x0 x0 A. 6 . B. 2 . C. 3 . D. 5 . Lời giải Chọn A
lim 2 f x  2.lim f x  2.3  6 x0 x0 x 15
Câu 21: ết qu của giới hạn lim là x2 x  2 A. 0 . B. 1. C.  . D.  . Lời giải Chọn D
 lim x 15  13   0   Ta có x2  . lim  x  2  0  x2 ì x 2 
nên x  2 . o đó x  2  0.  ậy x 15 lim   .  x2 x  2 2x  7 lim
Câu 22: Tính x3 x  3 . A.  . B.  . C. 0 . D. 2 . Lời giải Chọn A
Ta có: lim 2x  7  13  0 , lim  x  3  0 , x  3  x  3  0 .   x3 x3 2x  7 Vậy, lim    x3 x  . 3
Câu 23: Cho giới hạn lim  2 2
x  2ax  3  a   3 thì a bằng bao nhiêu? x 2 
A. a  2 .
B. a  0 C. a  2  . D. a  1  . Trang 10 Lời giải Chọn C
Ta có, lim  x  2ax  3 a    2  2 2 2 2 2  2a( 2
 )  3 a a  4a  7 . x 2  lim  2 2
x  2ax  3  a   3 . x 2  2
a  4a  7  3 . 2
a  4a  4  0 .  a  2  .
Câu 24: Hàm số nào sau đây liên tục tại x  2 ? 2 2x  6x 1 x 1 2 x x 1 2 3x x  2
A. f (x) 
. B. f (x)  .
C. f (x)  .
D. f (x)  . x  2 x  2 x  2 2 x  4 Lời giải Chọn A 2 2x  6x 1
Hàm số f (x) 
là hàm phân thức hữu tỉ xác định tại x  2 nên nó liên tục tại x  2 . x  2 2 2x  6 Câu 25: Tính lim  a b . hi đó 2 2
a b bằng x 3 x  3 A. 6 . B. 7 . C. 10 . D. 25 . Lời giải Chọn D  2    x  2 2 x 3 2 6  2x 3x 3 lim  lim  lim
 lim 2x  3  4 3. x 3 x 3 x 3 x 3 x  3 x  3 x  3 Suy ra 2 2
a  4, b  3  a b  25 .  x khi x  
Câu 26: Tìm giá trị của tham số m sao cho hàm số f x 3 1 1  
liên tục tại x  1  m khi x  1  o A. m  2  . B. m  2 . C. m  3 . D. m  0 . Lời giải Chọn A
Tập xác định của hàm số f x là D  . Ta có: f   1  m .
lim f x  lim 3x   1  3.  1 1 2  . x 1  x 1 
Hàm số đã cho liên tục tại x  1  f 1
  lim f x m  2  o khi     . x 1  Trang 11 Vậy m  2
 thỏa yêu cầu bài toán.
Câu 27: Tuổi thọ (năm) của 50 bình ác quy ô tô được cho như sau
Giá trị đại diện của nhóm 2,5;3 là A. 2, 9 . B. 2, 7 . C. 2, 8 . D. 2, 75 . Lời giải Chọn D 2, 5  3
Giá trị đại diện của nhóm 2,5;3 là:  2,75 . 2
Câu 28: Tuổi thọ (năm) của 50 bình ác quy ô tô được cho như sau
Cỡ mẫu của mẫu số liệu ghép nhóm trên là A. 50 . B. 48 . C. 14 . D. 6 . Lời giải Chọn A
Cỡ mẫu của mẫu số liệu ghép nhóm trên là: n  4  9 14 11 7  5  50
Câu 29: Tìm cân nặng trung bình của học sinh lớp 11B3 cho trong b ng bên dưới A. 56, 71 . B. 52,81. C. 53,15 . D. 51,81. Lời giải Chọn D
Trong mỗi kho ng cân nặng, giá trị đại diện là trung bình cộng của giá trị hai đầu mút nên ta có b ng sau
Tổng số học sinh là n  42 . Cân nặng trung bình của học sinh lớp 11B3 là
10.43  7.48 16.53  4.58  2.63  3.68 x   51,81(kg) 42
Câu 30: Cho hình chóp S.ABCD . Giao tyến của hai mặt phẳng SAC  và SBD là
A. Đường thẳng đi qua S và giao điểm của hai đường thẳng AB, CD . Trang 12
B. Đường thẳng đi qua S và giao điểm của hai đường thẳng AD, BC .
C. Đường thẳng đi qua S và giao điểm của hai đường thẳng AC, BC .
D. Đường thẳng đi qua S và giao điểm của hai đường thẳng AC, BD . Lời giải Chọn D
Ta có: S SAC SBD . O   AC  
SAC  OSAC
Trong  ABCD , gọi O AC BD thì  . O   BD  
SBD  OSBD
Vậy SO  SAC   SBD .
Câu 31: Cho tứ diện ABCD . Trên các cạnh AB và AC lấy hai điểm M và N sao cho AM BM và
AN  2NC . Giao tuyến của mặt phẳng  DMN  và mặt phẳng  ACD là đường thẳng nào dưới đây? A. DN . B. MN . C. DM . D. AC . Lời giải A M N B C D Chọn A
Giao tuyến của mặt phẳng  DMN  và mặt phẳng  ACD là đường thẳng DN .
Câu 32: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi  là giao tuyến chung của hai
mặt phẳng SAD và SBC  . Đường thẳng  song song với đường thẳng nào dưới đây?
A. Đường thẳng AB .
B. Đường thẳng AD . Trang 13
C. Đường thẳng AC .
D. Đường thẳng SA . Lời giải S A D B C Chọn B
Hai mặt phẳng SAD và SBC  có chung điểm S và lần lượt chứa hai đường thẳng song
song AD , BC nên giao tuyến  đi qua S và lần lượt song song với AD , BC .
Câu 33: Cho tứ diện ABCD . Gọi hai điểm M , N lần lượt là trung điểm của các cạnh AB, AC . Đường
thẳng MN song song với mặt phẳng nào sau đây?
A. Mặt phẳng  ABD .
B. Mặt phẳng  ACD .
C. Mặt phẳng  ABC  .
D. Mặt phẳng  BCD . Lời giải A N M B C D Chọn D
Vì MN là đường trung bình của tam giác ABC nên MN//BC mà BC   BCD nên
MN // BCD .
Câu 34: Cho hình hộp ABC . D A BCD
  có AC cắt BD tại O còn A C   cắt B D
  tại O . hi đó AB D
  song song với mặt phẳng nào dưới đây? A. A OC .
B. BDA .
C. BDC . D. BCD . Lời giải Trang 14 A B O D C A ' O' B' D ' C ' Chọn C
Vì BD//BD nên BD//  BDC . Vì AD//BC nên AD//  BDC .
Từ đó suy ra  ABD // BDC .
Câu 35: Xét một phép chiếu song song bất kì. Trong các mệnh đề sau, mệnh đề nào sai?
A. Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau.
B. Một đường thẳng có thể trùng với hình chiếu của nó.
C. Hình chiếu song song của hai đường thẳng chéo nhau có thể trùng nhau.
D. Một tam giác bất kỳ đều có thể xem là hình biểu diễn của một tam giác cân. Lời giải Chọn C Xét hình hộp ABC . D A BCD
  và phép chiếu lên mặt phẳng  AB C
 D theo phương chiếu AA . A B D C M A ' B' D ' C '
* Hai đường thẳng AD , BC chéo nhau và có hình chiếu là hai đường thẳng AD , B C   song song.
* Mọi đường thẳng nằm trên mặt phẳng chiếu có hình chiếu là chính nó.
* Xét hai đường thẳng chéo nhau a,b . Gọi P là mặt phẳng chứa a , hình chiếu của a trên
mặt phẳng chiếu Q là a . Vì b không thuộc  P nên hình chiếu của b không trùng a .
* Khi AB  AD thì mọi tam giác MBD ( M AA ) đều có hình biểu diễn là tam giác cân
ABD . Trang 15
II. PHẦN TỰ LUẬN (3,0 điểm). Câu Đ n Bi đi
Gi i phương trình sin 4x  cos5x  0 . 0.5
Ta có sin 4x  cos5x  0 0.25     cos5x  cos  4x    2    0.25 5x   4x k2  2 36   
5x    4x k2  2   x   k2  2   k    . 2
x    k  18 9 2  0.5 x  3  2  khi x  1
Cho hàm số f x   x 1
. Tìm m để hàm số liên tục tại 
  m  3 khi x 1 x  1. 0
Hàm số xác định tại x  1, f   1  m  3. 0.25 0 2 x 1 x   1  x   1
lim f x  lim  lim x 1  x 1    x   1  2
x  3  2 x 1 x   1  2 x  3  2 37 x 1 1  lim  . x 1  2   2 x 3 2
Hàm số đã cho liên tục tại x  1  lim f x  f   1  0.25 0 x 1  1 m  3  5  m  . 2 2 5 Vậy m  . 2
Một người muốn mua một thanh gỗ đủ để cắt ra làm các thanh 0.5
ngang của một cái thang. Biết rằng chiều dài các thanh ngang của
cái thang đó (từ bậc dưới cùng) lần lượt là 45 cm, 43 cm , 41 cm,, 31 cm . 38
Cái thang đó có bao nhiêu bậc? Tính chiều dài thanh gỗ mà người đó cần Trang 16
mua, gi sử chiều dài các mối nối (phần gỗ bị cắt thành mùn cưa) là không đáng kể.
Chiều dài các thanh ngang của cái thang (tính từ bậc dưới cùng) tạo thành một cấp số cộng có:    . 1 u 45;d 2 45  31 0,25 Suy ra n  1  8 . 2
o đó cái thang có 8 bậc. 845   31 Ta lại có   . 8 S 304 2 0,25
Vậy người đó cần mua thanh gỗ có chiều dài 304 cm.
Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông
và tô màu khác nhau như Hình 3. Tìm dãy số biễu diễn độ dài cạnh
của 8 hình vuông đó từ nhỏ đến lớn. Có nhận xét gì về dãy số 0.5 39 trên?
Ta có dãy số: 1;1;2;3;5;8;13;21 . 0,25
Nhận xét: Kể từ số hạng thứ ba, mỗi số hạng của dãy bằng tổng của hai số hạng liền trước. 0,25
-------------- HẾT -------------- Trang 17