Đề thi học sinh giỏi cấp tỉnh Toán 11 năm 2020 – 2021 sở GD&ĐT Lạng Sơn

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LẠNG SƠN
LỚP 11 NĂM HỌC 2020 - 2021
Môn thi: Toán lớp 11 THPT ĐỀ THI CHÍNH THỨC
Thời gian: 180 phút (không kể thời gian giao đề) Ngày thi: 18/3/2021
(Đề thi gồm 01 trang, 05 câu) Câu 1 (6,0 điểm).   
a) Giải phương trình sin 4x  cos x  1 sin 3x  2 cos 2x    .  4    y    1
x  y   x  y   1 y  x  2
b) Giải hệ phương trình 
 x, y  . 2 2
x y  8  y x  8  8  Câu 2 (3,0 điểm). n
a) Giả sử P x  1 3x 2
 a  a x  a x ... n  a x , với * n  . 0 1 2 n
Biết rằng a  a  405 n 1 , tính giá trị của a . 2 3   6
b) Cho tập hợp A  0;1;2;3;4;5;6; 
7 . Gọi S là tập hợp các số tự nhiên gồm 8 chữ số
đôi một khác nhau lấy từ A. Tính xác suất để lấy được số tự nhiên mà tổng 4 chữ số đầu
bằng tổng 4 chữ số cuối. u   2021   1
Câu 3 (3,0 điểm). Cho dãy số u được xác định bởi  . n  u 
 u  2021 n  1  n 1 n   Đặt 1 1 1 S    ... . Tính lim S . n n u u   u u  u u   u u  u u   u u  1 2 2 1 2 3 3 2 n n 1  n 1  n
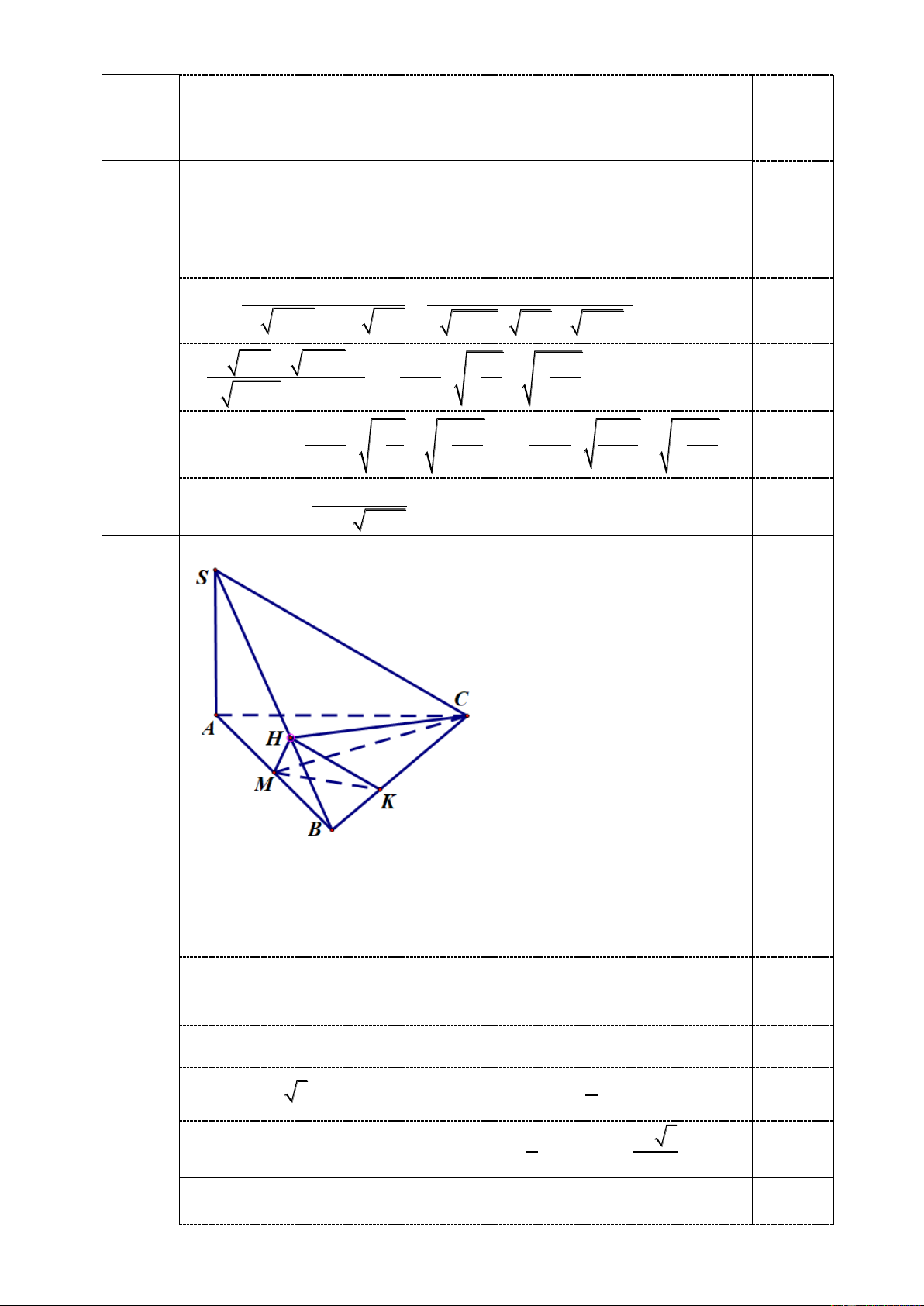
Câu 4 (6,0 điểm). Cho hình chóp tam giác S.ABC có đáy là tam giác đều cạnh bằng 2a .
Đường thẳng SA vuông góc với mặt phẳng  ABC . Gọi M là trung điểm của AB , H là
hình chiếu vuông góc của C lên SB và góc tạo bởi đường thẳng AB và mặt phẳng HCM  bằng 0 60 .
a) Tính diện tích tam giác HCM .
b) Tính sin của góc tạo bởi MH và SC . 1 ab
Câu 5 (2,0 điểm). Cho hai số thực dương a,b thỏa mãn a  b và  2 2 . Tìm giá b  a  2 1 a  2 1 b 
trị nhỏ nhất của biểu thức P  . 2 a  ab
---------------------Hết---------------------
Họ và tên thí sinh: ………………………………………………………....................... Số báo danh: …………..........................
Chữ kí giám thị số 1:………………................................……Chữ kí giám thị số 2:…......................……………………....
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LẠNG SƠN
LỚP 11 NĂM HỌC 2020 - 2021
HƯỚNG DẪN CHẤM THI MÔN TOÁN LỚP 11 THPT
(Hướng dẫn chấm gồm 04 trang)
Chú ý: Những cách giải khác HDC mà đúng thì cho điểm theo thang điểm đã định. Câu Nội dung Điểm 1        
(6,0 đ) a) Giải phương trình sin 4x cos x 1 sin 3x 2 cos 2x    4 
PT  sin 4x  cos x  1 sin 3x  cos 2x  sin 2x 0,5  x x  x  x    2 2sin 3 cos sin 3 cos 1 2cos x   1  0 0,5  x x   2 sin 3 2cos
1  cos x  2cos x  0 0,5  2cos x  
1 sin3x  cos x  0 0,5  Với 1 cos x 
 x    k2 ,k  0,5 2 3    x   k     Với 8 2
sin 3x  cos x  sin 3x  sin  x     , k  0,5  2  
x   k  4   y    1
x  y   x  y   1
y  x  2   1 b)  2 2
x y  8  y x  8  8  2 Điều kiện 2
x  y  0, y  0, x  8  0 Phương trình   1   y   1
x  y   x  y   1
y  y 1 x  y 1 0,5   y  
1  x  y  
1   x  y   1  y   1  0  y  
1  x  y   1
x  y   1  y   1    0 0,5 x  y 1 y 1   
 y  x  y   1 1 1 1     0   x  y 1 y 1   0,5  y 1  0  y 1   1 1   (do   0) x  y 1  y  x 1 x  y 1 y 1
Với y  1 thế vào 2 ta được:  8 x  0,5 2 3x  x  8  8   3  x  3 2 2 9
 x  48x  64  x  8
Với y  x 1 thế vào 2 ta được: 2 x x  x   x   2 2 9 1 x  8  8 0,5 x  x x  x  2 2 2 2 2 9 1 x 8 8         
 x  x   x   x    x   x  2 2 2 2 2 2 7 2 1 8 0 1 8  0 x 1  9 2
 x  8  x 1    x  x  8   x  2 2 1 2 Với 9 7 x   y  0,5 2 2   
Vậy nghiệm của hệ phương trình là  x y     9 7 ; 3;1 , ;     2 2  2 n
a) Ta có P  x k
 C 3k. k k
x  a  C .3k (3,0 đ) n k n k 0
Theo giả thiết ta có a  a  405n   2 3
1  9C  27C  405 n 1 2 3 n n  
Điều kiện n  3,n 0,5 9
 nn   9 1  nn  
1 n  2  405n   1 2 2 n 10 2
 n  n  90  0   n  9  (L) 0,5 Khi đó 6 6 a  C .3 6 10
b) Số tự nhiên gồm 8 chữ số đôi một khác nhau lấy từ A là 0,25
nS   8! 7!
Ta có 0 1 2  3  4  5  6  7  28 nên để tổng của 4 chữ số đầu
bằng tổng 4 chữ số cuối thì tổng của 4 chữ số phải bằng 14
Ta lập 4 bộ số có tổng bằng 14 có chứa chữ số 0 là:  0,25 0,1,6,  7 ,0,2,5,  7 ,0,3,4,  7 ,0,3,5,  6
Với mỗi bộ số có chứa chữ số 0 trên tương ứng với bộ còn lại
không chứa chữ số 0 và có tổng bằng 14
TH1: Bộ có chữ số 0 đứng trước: có 4 bộ có chữ số 0, ứng với mỗi bộ có:
+) Xếp 4 số đầu có 3.3! cách. 0,5
+) Xếp 4 số cuối có 4! cách.
Áp dụng qui tắc nhân có 4.3.3!.4!1728 số.
TH2: Bộ có chữ số 0 đứng sau: có 4 bộ có chữ số 0 , ứng với mỗi bộ có:
+) Xếp bộ không có chữ số 0 đứng trước có 4! cách. 0,5
+) Xếp bộ có chữ số 0 đứng sau có 4! cách.
Áp dụng qui tắc nhân có 4.4!.4!  2304 số.
Gọi B là biến cố mà số tự nhiên mà tổng 4 chữ số đầu bằng tổng 4
chữ số cuối nên nB 1728  2304  4032 số thỏa mãn yêu cầu 0,5 bài toán. n B Vậy xác suất biến cố 4
B là: P  B     nS  35 3 Ta có u
 u  2021 u u  2
 021 0 nên u là dãy số n  n 1  n n 1  n (3,0 đ) giảm Giả sử  1,0 u
bị chặn dưới tức là tồn tại limu  a  2  021 n  n
Qua giới hạn hai vế ta được a  a  2021 (vô lý) tức là limu   n 1 1 Ta có  0,5 u u   u u     u u u   u  n n 1 n 1 n n n 1   n n 1   u   u    n n 1 1 1 1           0,5  u u u  u 2021 u u n n 1   n 1  n   n n 1       Khi đó 1 1 1 1 1 1 S              0,5 n 2021 u u  2021 2021 u   1 n 1    n 1   Vậy 1 lim S   0,5 n 2021 2021 4
a) Tính diện tích tam giác HCM . (6,0 đ) C  M  SA Ta có 
 CM  SAB  CM  SB  1 C  M  AB 0,5
Mặt khác CH  SB2 . Từ  
1 và 2  SB  CMH  AB   HCM   M Lại có 
  AB,HCM  0   0,5 BH   HCM  BMH 60
Do CM  SAB  CM  MH hay tam giác HCM vuông tại M 0,5 a
Có CM  a 3 ; 0
BM  a  MH  M . B cos 60  0,5 2 2 Vậy diện tích tam giác 1 a 3 HCM là S  CM.MH  0,5 H  CM 2 4
b) Tính sin của góc tạo bởi MH và SC .
Trong tam giác SBC dựng HK / /SC K  BC 0,5
Khi đó MH,SC  MH, HK  a 3
Trong tam giác BMH có 0 BH  M . B sin 60  2 Ta có a 0,5 2 . a SA AB A . B MH 2a 3 2 S  AB  M  HB    SA    MH BH BH a 3 3 2 4a 3 2 2 SB  SA  AB   SC 0,5 3 BH HK BK a 3 3a HK / /SC   
 HK  BH  ; BK  0,5 SB SC BC 2 4
Trong tam giác MBK có a 13 0,5 2 2 2 0
MK  BM  BK  2BM .BK.cos 60  MK  4 2 2 2
MH  HK  MK 3
Trong tam giác MHK có cos MHK   0,5 2MH.HK 8
Vậy sin MH,SC 61 2  1 cos MHK  0,5 8 5
Theo giả thiết ta được (2,0 đ)  0,5 b  a b a 1 2 2
1 ab  2 ab    a b 2 Đặt b t  ,t  0 ta được a 0,5 1 1 b a 1 t    t  2   2   t 2 a b 2  2  a  2 1
1 b  b  a2  ab  2 1 9ab  2 1 Ta có P    0,5
a a  b
a a  b
8a a  b ab  2 9 1 Mặt khác 9.4ab 9 9    
8a a  b
8a a  b 3  a   1  2 1 2 1      b   2  0,5 Vậy 1
P  3  min P  3  a  ,b  2 2